1. Introduction

In the present day, image processing has wide applications in multiple fields, including intelligent surveillance, medical imaging, and autonomous driving. With the advancement of technology and the increase in market demand, there is a growing need for high-performance, low-power consumption, and multifunctional integrated image processing platforms.

To meet this demand, this paper develops an image processing system based on FPGA. This system has the capability of high-speed data transmission and processing, meeting the requirements for large-scale image data processing. The system features multifunctional integration and self-designed underlying IP, offering strong market competitiveness and broad application prospects. It can satisfy the high-performance, low-power consumption needs in different fields of image processing, providing robust support for practical application scenarios.

2. FPGA system design architecture

The overall design architecture of the real-time video processing system based on FPGA is shown in Figure 1. The system is built on the Anlogic PH1A90 FPGA chip and consists of image acquisition, image processing, and image display subsystems. First, video data is captured using a stereo camera. After image fusion, the image data is stored in Double Data Rate Synchronous Dynamic Random Access Memory (DDR SDRAM). The image processing module reads data from the DDR and performs a series of operations on the image source, such as color space conversion, histogram equalization, noise reduction, and sharpening, to enhance the image quality. The processed image is then displayed via the High Definition Multimedia Interface (HDMI), facilitating visual observation and debugging.

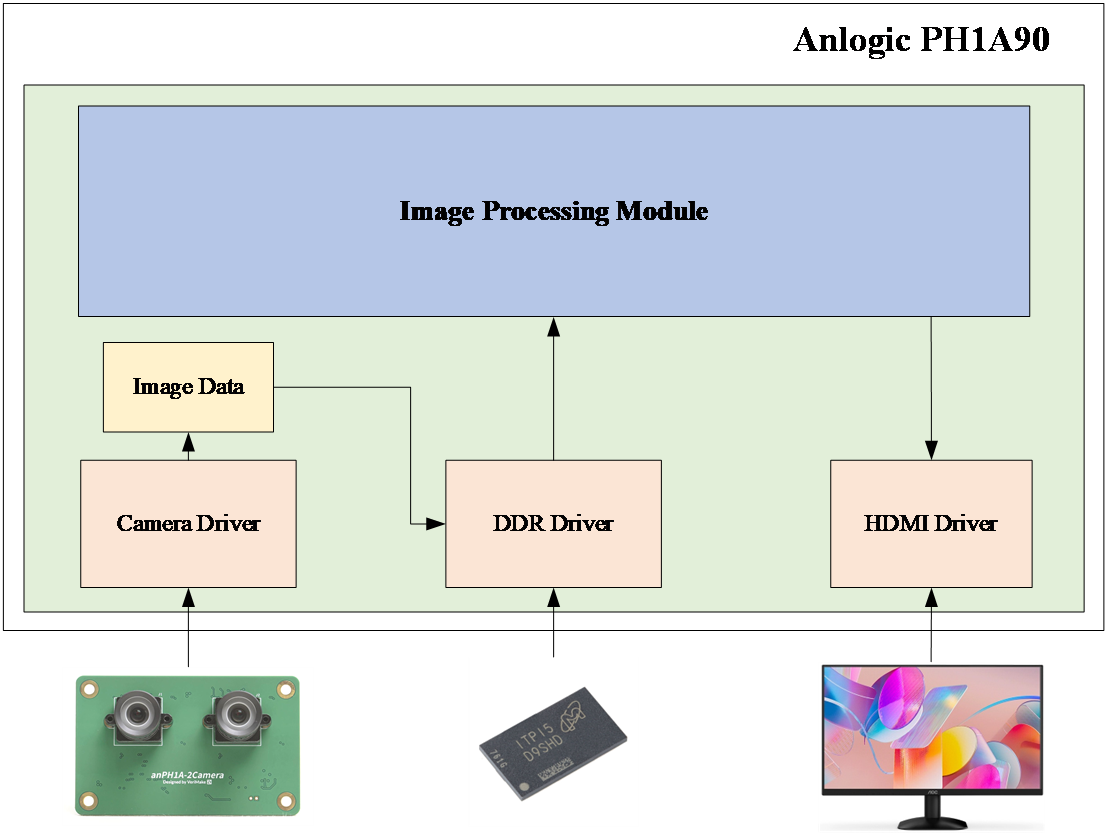
Figure 1. Overall System Design Architecture

3. Design of the image processing module

3.1. Color space conversion

To achieve the output of color images, it is necessary to process the data of three channels. To save resources, only the grayscale of RGB888 is extracted, and the grayscale image is processed separately in the subsequent stages. This involves converting the RGB888 model to the YCbCr model and processing the Y channel. The conversion relationship between RGB888 and YCbCr models is as follows [1]:

\( \begin{cases}Y=0.299R+0.587G+0.114B \\ Cb=0.568(B-Y)+128=-0.172R-0.339G+0.511B+128 \\ Cr=0.713(R-Y)+128=0.511R-0.428G-0.083B+128\end{cases} \)

\( \begin{cases}R=Y+1.371(Cr-128) \\ G=Y-0.698(Cr-128)-0.336(Cb-128) \\ B=Y+1.732(Cb-128)\end{cases} \)

3.2. Bilateral filtering

Bilateral filtering is a nonlinear filtering technique used in image processing that aims to denoise and smooth the image while preserving edge information by considering both the spatial neighborhood and the pixel intensity values [2]. The bilateral filter processes each pixel in the image by determining its new intensity value through a weighted average of neighboring pixels. The weights used in the average are spatial weights and intensity weights, where the spatial weight depends on the spatial distance between pixels—the farther the distance, the smaller the weight; the intensity weight depends on the intensity difference between pixels—the greater the intensity difference, the smaller the weight. The filter response of the bilateral filter can be expressed as:

\( I^{ \prime }(x)=\frac{1}{W_{p}}\sum_{x_{i}∈S}I(x_{i})\cdot f_{s}(‖x_{i}-x‖)\cdot f_{r}(|I(x_{i})-I(x)|) \)

where \( I(x) \) is the value of the original image at pixel \( x \) ; \( I^{ \prime }(x) \) is the value of the filtered image at pixel \( x \) ; \( S \) is the spatial neighborhood containing pixel \( x \) ; \( f_{s}(‖x_{i}-x‖) \) is the spatial weight, usually a Gaussian function used to consider spatial distance; \( f_{r}(|I(x_{i})-I(x)|) \) is the intensity weight, also usually a Gaussian function used to consider intensity differences.

The spatial weight considers the geometric distance between pixels, commonly using the Gaussian function form:

\( f_{s}(d)=e^{-\frac{d^{2}}{2σ_{s}^{2}}} \)

where \( d \) is the Euclidean distance between two pixels; \( σ_{s} \) controls the decay rate of the spatial weight.

The intensity weight considers the difference between pixel intensities, also commonly using the Gaussian function form:

\( f_{r}(d)=e^{-\frac{d^{2}}{2σ_{r}^{2}}} \)

where \( d \) is the difference in pixel intensity values; \( σ_{r} \) controls the decay rate of the intensity weight.

3.3. Histogram equalization

Histogram equalization is a technique used to enhance image contrast by adjusting the distribution of grayscale values in an image, making the histogram distribution of the image more uniform and thereby improving the overall visual effect of the image [3]. This method is widely used in image processing and computer vision, especially for enhancing details in low-contrast images. Histogram equalization redistributes the grayscale levels of the original image so that the grayscale distribution of the output image is as uniform as possible. The basic idea is to use the cumulative distribution function (CDF) to map the grayscale values of the original image to a new range of grayscale values [4]. The operation steps are as follows [5]:

(1) Calculate the histogram of the original image: Count the frequency of each grayscale value in the image to obtain the probability distribution of the grayscale values.

(2) Calculate the cumulative distribution function (CDF): The cumulative distribution function represents the cumulative percentage of the number of pixels at or below a certain grayscale level. The cumulative distribution function can be obtained by accumulating the sum of the original histogram. Let the grayscale levels of the original image be \( L \) , the number of pixels at grayscale value \( i \) be \( n_{i} \) , and the total number of pixels in the image be \( N \) . The cumulative distribution function \( CDF(i) \) is expressed as

\( CDF(i)=\sum_{j=0}^{i}\frac{n_{j}}{N}\sum \)

(3) Grayscale value mapping: Use the cumulative distribution function to map the grayscale values of the original image to a new range of grayscale values. Let the grayscale range of the original image be \( [0，L-1] \) and the new grayscale value after equalization be \( h(i) \) . Then,

\( h(i)=(L-1)×CDF(i) \)

(4) Generate the equalized image: Replace the grayscale value of each pixel in the original image with the new grayscale value to generate the equalized image.

3.4. Sobel sharpening

The purpose of image sharpening is to make the edges of objects in an image clearer. One of the simplest ways to achieve this is to first extract the edge information of the image and then overlay it onto the original image, thereby enhancing the edges of the image. In FPGA, the Sobel operator is used for this computation. By combining the horizontal and vertical gradients and taking the modulus, the final gradient is obtained, which is then superimposed onto the original image to achieve the sharpening effect [2].

The convolution factors of the Sobel operator for the horizontal and vertical gradients, \( G_{x}G_{x} \) and \( G_{y}G_{y} \) , are as follows:

\( G_{x}=[\begin{matrix}-1 & 0 & 1 \\ -2 & 0 & 1 \\ -1 & 0 & 1 \\ \end{matrix}][\begin{matrix} & & \\ & & \\ & & \\ \end{matrix}] \)

\( G_{y}=[\begin{matrix}-1 & -2 & 1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \\ \end{matrix}][\begin{matrix} & & \\ & & \\ & & \\ \end{matrix}] \)

The final gradient \( G \) is obtained by combining the horizontal gradient \( G_{x} \) and the vertical gradient \( G_{y} \) and taking the modulus, which extracts the edge information of the image:

\( G=\sqrt[]{G_{x}^{2}+G_{y}^{2}} \)

Finally, the extracted edge information of the image is superimposed on the original image to achieve the sharpening effect:

\( I^{ \prime }(x)=I(x)+G \)

where \( I(x) \) is the value of the original image at pixel \( x \) , and \( I^{ \prime }(x) \) is the value of the sharpened image at pixel \( x \) .

4. FPGA verification

First, the original video source undergoes white balance adjustment. The color space is converted from RGB to YCbCr. Next, random noise is removed through bilateral filtering, and brightness response is matched using histogram equalization, followed by sharpening the image using the Sobel operator to enhance edges. The algorithmic processing effects are shown in Figure 2.

(a) RGB to YUV Effect

(b) Bilateral Filtering Effect

(c) Histogram Equalization Effect

(d) Sobel Sharpening Effect

Figure 2. Algorithmic Processing Effects

5. Conclusion

This system addresses real-time issues in video image processing by optimizing image processing algorithms on FPGA. These include color space conversion, bilateral filtering, histogram equalization, and Sobel sharpening algorithm. Experimental validation indicates that the system performs well in image processing, achieving high real-time performance and demonstrating high portability, thus presenting significant application value in the field of image processing.