I. Introduction

Shock dynamics is a discipline to study the dynamic response of an object under the action of shock waves, and its main research includes: the propagation law of shock waves in the medium, the process and mechanism of interaction between shock waves and the surface of the object, as well as the effect of shock waves on the structure and performance of the object [1]. With the continuous development of science and technology and the continuous expansion of application fields, shock dynamics has become an important engineering field and has been widely used in the fields of automobile collision, aerospace, building structure, etc. The SPH (Smoothed Particle Hydrodynamics) method is a numerical simulation method based on the principle of particle hydrodynamics. The SPH (Smoothed Particle Hydrodynamics) method is a numerical simulation method based on the principle of particle hydrodynamics, which describes the fluid's motion state by discretising a continuous medium into a series of particles and calculates the fluid's physical properties by using the interactions between these particles. Due to its advantages of high computational accuracy and high efficiency when dealing with large-scale data, the SPH method has been widely used in the study of impact dynamics [2]. At present, scholars at home and abroad have proposed many numerical simulation algorithms for impact dynamics based on the SPH method and achieved certain research results. However, in practical applications, the SPH method still has some problems, such as low computational accuracy and low efficiency when dealing with large-scale data, which limits its application and development in practical engineering [3].

The aim of this study is to explore several issues of shock dynamics based on the SPH method in order to improve the accuracy and efficiency of numerical simulation. Specifically, we will focus on the following aspects: firstly, we will conduct an in-depth study on the nonlinear phenomenon and its influencing factors during the propagation process of shock waves; secondly, we will investigate the process and mechanism of the interaction between the shock wave and the surface of the object and propose a corresponding numerical simulation algorithm; finally, we will optimize and improve the proposed algorithm by combining with the existing relevant literature and research results. This study can provide more accurate and reliable numerical simulation support for practical engineering applications, and also help to promote the development and progress of the field of impact dynamics.

2. Basic principles and implementation of the SPH methodology

2.1 Fundamentals and mathematical description of the SPH approach

The SPH (Smoothed Particle Hydrodynamics) method is a numerical simulation method based on the principles of particle hydrodynamics. The basic principle is to discretise a continuous medium into a series of particles and use the interaction between these particles to calculate the physical properties of the fluid [4]. Specifically, assuming that a continuous medium is discretised into N particles of mass m, the position and velocity of each particle can be expressed as:

\( x = x0 + v0 * t \)

\( y = y0 + v1 * t \)

\( z = z0 + v2 * t \)

where (x0, y0, z0) is the initial position of the particle and (v0, v1, v2) is the velocity of the particle. In the SPH method, the density function D(r) is defined as the sum of the distances of all the particles to some centre point r divided by the total mass M:.

\( D(r) = (1/M) * ∑i=1N d\_i^2 \)

where d_i is the distance from the ith particle to the centre point r. To avoid the problem of infinity when the distance is zero, a very small value of epsilon is usually added to the distance. the density function can be further decomposed into a function with respect to the radial coordinate ρ and the angle θ. The density function can be further decomposed into a function with respect to the radial coordinate ρ and the angle θ:

\( D(\\rho, θ) = (1/M) * ∑i=1N 4/π * ε^3 * (1-cos(θ)) * sin^2(θ) * d\_i^2 \)

where ε is a very small positive number that controls the degree of smoothing of the density function. The density function D(rho, θ) can be obtained by solving a system of nonlinear equations. In addition, the SPH method needs to consider factors such as the interaction force between particles and the range of action to ensure the accuracy and stability of the numerical simulation.

2.2 Implementation process and technical details of the SPH methodology

The implementation process of the SPH method consists of the following main steps:

Firstly, the continuous medium needs to be discretised into a series of particles of mass m and radius r. The purpose of this step is to facilitate the subsequent calculation and processing of the particles [5]. Second, the density function needs to be constructed based on factors such as the distance between particles and the range of action. The density function is an important parameter describing the distribution of particles, and its accuracy directly affects the accuracy of the numerical simulation results. Third, the interaction force needs to be calculated according to the interaction force formula between particles. The interaction force determines the degree of interaction between particles, and its size and direction need to be calculated accurately [6]. Fourth, the positions and velocities of the particles are updated according to the density function and the interaction force. This step is the most critical step in the whole simulation process, and it is necessary to ensure that the update speed and accuracy can meet the requirements. Finally, the above steps need to be repeated until the required time or accuracy is achieved. In the process of iterative solution, attention should be paid to control the convergence and stability of the calculation.

In the implementation of the SPH method, the following technical details need to be noted:

1. How to select the appropriate number of particles N and particle size r. The selection of the number of particles and particle size has an important impact on the calculation accuracy and efficiency and needs to be weighed and selected according to the actual problem [7].

2. How to construct the density function and how to deal with the situation where the distance is zero. The construction of the density function needs to take into account factors such as distance and range of action, and at the same time, it needs to deal with the case where the distance is zero to ensure the accuracy and stability of the calculation.

3. How to calculate the interaction force between particles and how to control the range of action. The calculation of the interaction force needs to consider the direction and size of the force, and the control of the range of action can reduce the complexity of the calculation and improve the efficiency of the calculation.

4. How to balance issues such as computational accuracy and computational efficiency. In the implementation of the SPH method, it is necessary to balance factors such as computational accuracy and computational efficiency. Too high accuracy requirement will increase the complexity of calculation and calculation time, while too low accuracy may lead to inaccurate results. Trade-offs and choices need to be made according to the actual problem.

2.3 Development and implementation of numerical simulation software for impact dynamics based on the SPH methodology.

The development and implementation of numerical simulation software for shock dynamics based on the SPH method is an important goal of this study. The main functions of this software include the following aspects: firstly, it supports a variety of shock wave models and parameter settings, including, but not limited to, static fluid model, dynamic fluid model, and one-dimensional shock wave model. These models can meet the needs of different shock dynamics problems, and the parameters can be adjusted according to the actual situation to achieve more accurate numerical simulation [8]. And the software supports a variety of material models and parameter settings, including elastic materials, plastic materials, hyperelastic materials and so on. These material models can simulate the physical properties of different materials, and the parameters can be adjusted as needed to achieve more accurate material response simulation. Finally, the software also supports large-scale data processing and computation, and can use distributed computing and other technologies to achieve rapid data processing and computation, thus improving simulation efficiency and accuracy [9].

In the process of software development, it is necessary to consider the basic principles and mathematical description of the SPH method, and to design and optimise the technical details in combination with the actual situation. For example, it is necessary to choose appropriate discretisation schemes, time integration methods, particle arrangement methods, etc., to achieve more accurate numerical simulation. At the same time, it is also necessary to focus on user experience and ease of use, for example, a user-friendly interface design and detailed help documents can be adopted to facilitate the operation of numerical simulation of impact dynamics.

3. Key issues and research methods in impact dynamics

3.1 Non-linear phenomena in shock wave propagation and their influencing factors

The nonlinear phenomenon in the process of shock wave propagation and its influencing factors is an important direction in the study of shock dynamics. In practice, due to the nonlinearity and nonuniformity of the medium, some complex nonlinear phenomena will appear in the process of shock wave propagation, such as wave peaks and troughs interlacing, waveform distortion, multiple waveforms and other phenomena, which will have a certain impact on the study of shock dynamics [10]. The appearance of nonlinear phenomena is closely related to the nature of the medium itself and the propagation conditions of the shock wave. For example, when a high-speed vehicle hits an obstacle, due to the interaction between the vehicle and the obstacle, the propagation of the shock wave will be greatly affected, and complex waveforms and fluctuation patterns may appear. In addition, the non-uniformity of the medium itself will also have an effect on the propagation of shock waves, such as the interface between different materials, defects and holes inside the medium.

In order to better simulate and predict these nonlinear phenomena, more refined numerical simulation methods and algorithms are needed. The SPH method is a commonly used numerical simulation method, which can effectively simulate the propagation process of shock waves, but it has certain limitations of its own, such as low computational efficiency, poor numerical stability and other problems. Therefore, the SPH method needs to be further improved and refined to enhance its computational efficiency and stability, and better simulate and predict the nonlinear phenomena in the process of shock wave propagation [11]. Therefore, the nonlinear phenomena in the process of shock wave propagation and their influencing factors are an important direction in the study of shock dynamics, which need to be studied in depth and more refined numerical simulation methods and algorithms need to be used to simulate and predict these phenomena.

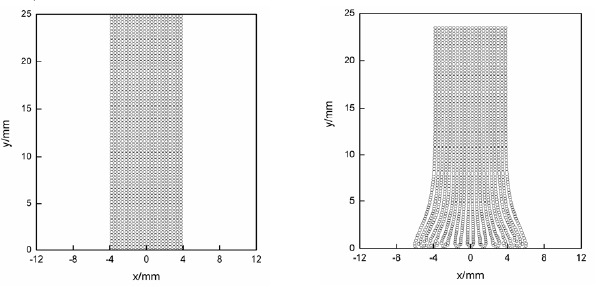
Figure 1. Nonlinear phenomena during shock wave propagation

3.2 Research on the process and mechanism of interaction between shock wave and object surface

Shock wave interaction with object surface is a very important issue in impact dynamics. In many practical applications, such as car collisions, explosions, and material impact tests, an in-depth understanding of the process and mechanism of the interaction between shock waves and object surfaces is required to improve the accuracy and reliability of numerical simulations. The interaction of shock waves with the surface of an object involves complex physical processes, including the propagation of stress waves, the dynamic response of materials, and the absorption and reflection of energy. These physical processes are affected by a variety of factors, such as the shape, speed, and frequency of the shock wave, and the shape, material, and size of the object. Therefore, appropriate numerical simulation methods and algorithms are needed to accurately simulate and predict the interaction processes between shock waves and object surfaces [12].