1. Introduction

In the past few decades, people's demand for the Internet is increasing due to its rapid development. Consequently, while people are enjoying the convenience of the Internet in obtaining information, each user's requirements for private use experience are also increasing, that is, the requirements for personalized online recommendations are constantly increasing, and independent personalized customization is realized for each user. The recommendation and display system application can greatly improve the user's satisfaction with browsing and using this content, thereby further expanding the user volume and return rate of the product. Therefore, customizing personalized recommendation services for target users has become an important research issue for numerous Internet digital information product companies. As a result, a diverse array of recommendation algorithms has been applied to products in people’s daily life.

There are an infinite set of gambling machines placed in front of the user, and it is up to the user to decide which arm to pull each time (each machine is assigned a different reward) [1]. The samples which are from each arm of the machine should be independently and identically distributed. At the same time, the conversion rate of each arm of the machine is fixed and will not be affected by time. At the same time, the delay is absent in the process of pulling the arm and observing the result. Even with the delay, the delay is far less than the delay between opportunities to pull the arm. Using standard slot machines is perfectly reasonable when these assumptions are true. As long as these assumptions do not hold, the underlying multi-armed bandit algorithm will not work properly in certain scenarios [2]. Due to the lack of assumptions, these algorithms are also usually much slower to converge, usually too slow to converge, and few people use them in practice [3].

Therefore, the algorithms that are widely used in various Internet digital information products are usually multi-armed bandit algorithm and algorithms based on it to a certain extent. In the field of recommendation systems, available items are often modeled as arms which will be pulled. Choosing an arm can be seen as recommending a product, and the user's response is regard as the reward (e.g. click, accept, satisfaction, etc.). Just like traditional reinforcement learning scenarios, to achieve its goals, the dilemma of exploitation and exploration should be balanced well. Exploitation is actually pulling the rewards that have earned the maximum rewards in the whole rounds, get the maximum value of the short-term reward value of the system, while recommend other rewards to achieve explorations, which can be used to increase user's personal information and content-related information, so that the long-term rewards of the system can be maximized. However, the traditional multi-armed bandit algorithm can hardly be directly used in field of the recommended system due to its own limitations in practical applications. At the same time, with the increasing demand for recommendation system algorithms, although the improved algorithms based on the traditional multi-armed bandit algorithm used by each recommendation system have been improved in different aspects, there is no corresponding multi-armed bandit algorithm summary in the field of recommendation systems. Therefore, it is very necessary to summarize and review the recommendation algorithms used in the field of recommendation systems.

Therefore, this paper summarizes the recommendation algorithms based on multi-armed bandit algorithm mainly used in the current Internet digital information product recommendation system, and provides the pertinence of the recommendation algorithm in different application scenarios for different application scenarios of the recommendation algorithm Interpretation and analysis. At the end of this paper, the algorithm which is based on the Multi-Armed Bandit (MAB) algorithm and used in the current recommendation system is proposed for the improvement space and prospect of the future use in the recommendation system.

2. Method

2.1. Introduction of MAB in recommendation

To alleviate the situation of information overload, personalized online recommendation system customizes satisfactory products for different users. It faces a trade-off between two purposes: to improve user satisfaction in the long-term, and to achieve this goal by exploring new items. At the same time, known information is exploited to recommend items and information content that have been interacted with. The main problem in this type of situation is the dilemma of exploration and exploitation.

Figure 1 is a demonstration of using the MAB problem as an example to model the problem of personalized online recommendation. The overall process is roughly that the agent will sequentially select an action (arms) in a set of actions with an unknown distribution of rewards (rewards are unknown but fixed), and at the same time observe the reward of the selected action (arms), and provide reference information for the reward for the next selected action by observing the obtained reward results. When in the exploration situation, a new selection action will be performed. When it comes to exploitation, the recommendation system will refer to the reward feedback information obtained through the previous observation and select the action (arms) which has the highest reward according to the reward reference information. In the case of the agent performs a selection action, a corresponding reward will be generated, and the generated reward information will also help the agent to perform the next selection action. By adopting this mechanism, cumulative rewards can be maximized, or cumulative regrets can be minimized over time.

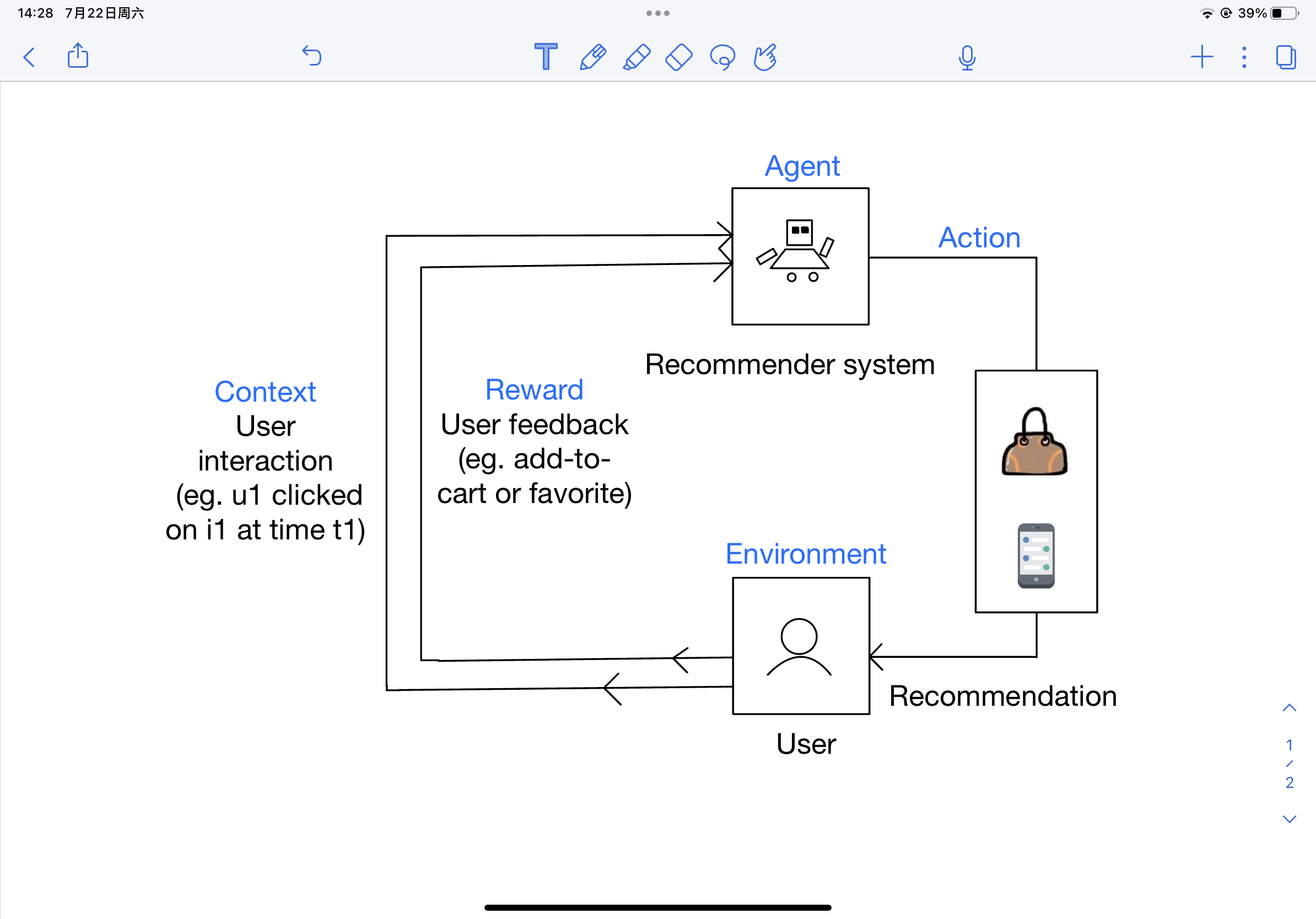
Figure 1. Modeling Online Recommendation Task Based on MAB (Multi-Armed Bandit) Problem. Names which are black mean definitions in the recommendation process. Names which are blue mean definitions in bandit questions [4].

2.2. The details of dynamic clustering based contextual combinatorial multi-armed bandit (DC3MAB)

In practical applications, selecting an algorithm that can accurately and quickly personalize recommendations based on context information content is an important issue in recommender systems. Structure of recommended system based on Dynamic clustering based contextual combinatorial multi-armed bandit (DC3MAB) shown in Figure 2 is mainly composed of four parts, namely part (a), cluster user, part (b), item partitioning, part (c), bandit and part (d), output. Part (a) is responsible for calculating the similarity of users and clustering user groups with high similarity. At the same time, the input is a sequence of interactive actions. Part (b). The task of part(b) is to divide the items into distinct subsets, and these subsets are going to be used as a bandit's super arm. Part (c) is responsible for using the bandit strategy to generate candidate recommendation sequences for user u. Finally, part (d) is responsible for outputting Output the corresponding items, the feedback results and reward information for part (a) and part(b) [4].

The super arm in the algorithm and the subset of items modeled as arms through dynamic item division can further broaden the types of recommended content and can also avoid the problem of large amount of calculation caused by large project scale and large number of users. The DC3MAB algorithm realizes the link between users with high similarity by using the dynamic user clustering strategy, and solves the problem caused by huge amount of user and project data. Therefore, the DC3MAB algorithm can be well applied in the recommendation system due to its good recommendation accuracy and a small amount of calculation.

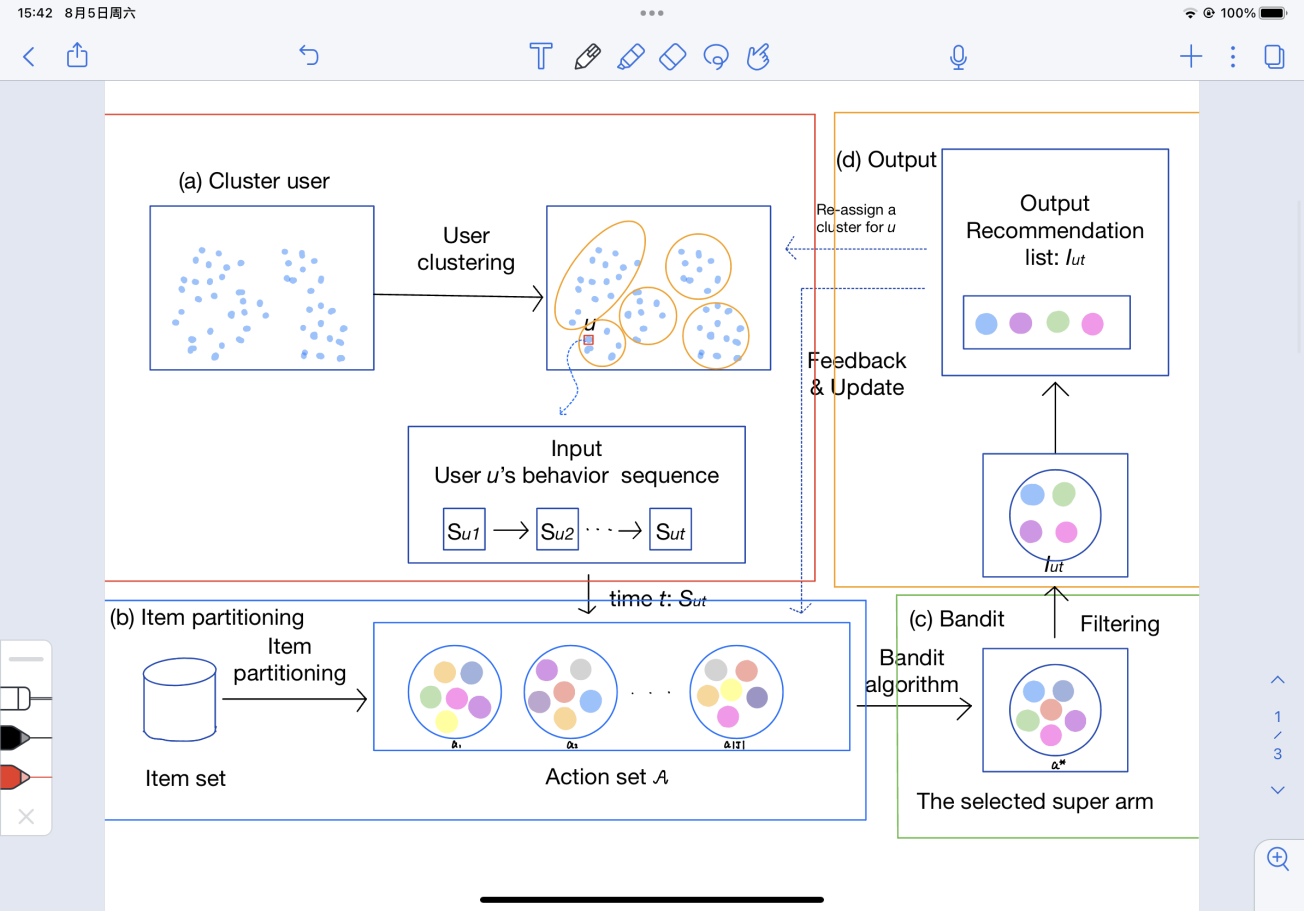
Figure 2. Structural diagram of recommendation system based on DC3MAB (Details of Dynamic clustering based contextual combinatorial multi-armed bandit) [4].

2.3. Binary upper confidence bound (BiUCB)

2.3.1. Introduction. There is a common problem in web-based environments - the cold start problem [5], in which there is no information about user or item preferences [6]. Binary upper confidence bound (BiUCB) is a contextual bandit algorithm for cold-start and diversified recommendation. When solving the above problems, BiUCB is an algorithm that can handle such problems well. At the same time, BiUCB and k-ε-greedy can be combined as a mutual switching algorithm. Modeling the cold start problem based on the contextual multi-armed bandit problem. Contextual multi-armed bandit is a form evolved from multi-armed bandit. Correspondingly, Upper Confidence Bound (UCB) is a good solution to the contextual multi-armed bandit algorithm. Generally speaking, UCB recommends that the arm has maximal confidence upper bound. In the case of the agent selects a corresponding content for the current person, it can be understood that is the agent that selects items for the current user. BiUCB tracks the dynamics of users and items by assuming that the current user and items are each other's arms.

2.3.2. Algorithm Details. BiUCB includes two contextual bandit algorithm models, namely BIUCB and B2UCB, both of which are called BiUCB. In this algorithm, remember that users and items are each other’ s arms, the function of B1UCB is responsible for selecting recommended items for each independent user, and the function of B2UCB is to passively select the corresponding user for each item for matching. The way LinUCB extends UCB is to consider the context information content related to the arm [7]. At the same time, if the system wants to recommend a variety of items, you will send a group of the items to each user through entropy regularization, which is called the super arm.

In this algorithm, the user is assumed to be an arm. BiUCB will require each user to treat each item passively. After BiUCB selects the corresponding recommended content for the user, it will get the reward of super arm. When BiUCB recommends content to users, these items are regarded as arms, and then algorithm will select the arm which has the largest upper bound of the confidence interval as the selection object. Based on UCB's strategy, BiUCB proposes the largest upper bound of the confidence interval between these arms, while the selected item also has an upper bound of high probability. The way the agent adjusts its strategy is to optimize the user's preference information. With each arm passively selecting users, rewards can be shared between both users and items. Therefore, the algorithm will not only track the dynamic situation of the user but also track the dynamic situation of the project at the same time. The profile of the items under the assumption of the algorithm is fixed, but the feature vector of the items is not constant but will continue to change [8].

After that, the algorithm will add an oracle function to the reward function, the goal of the oracle function is to measure the correlation and diversity. The oracle function is an artificially defined function. Accordingly, the oracle function can be used to solve combinatorial optimization problems.

3. Applications and discussion

Personalized recommendation system: The multi-armed bandit algorithm can be applied to a personalized recommendation system. By analyzing users' personal preferences, behavior patterns, and contextual information, algorithms can accurately predict users' preferences for various options in a specific context, and accordingly recommend to users the content or products that align optimally with their unique preferences [9].

Online advertising optimization: The multi-armed bandit algorithm can also be applied to online advertising optimization. In this application scenario, the algorithm can dynamically select the most attractive and clickable advertisement style, location and display time according to the needs of different advertisers and the contextual information of the advertising platform, thereby improving the effect and revenue of advertisement placement.

Analysis of potential user characteristics: Using the multi-armed bandit algorithm, the effect of advertisements displayed to different potential user groups can be analyzed. By mining basic user information, behavior habits, hobbies, etc. Users can be divided into different characteristic groups, and then different advertisements can be displayed for different characteristic groups. By comparing the performance of different advertisements in different characteristic groups, the best advertising strategy for each user characteristic group can be determined to achieve advertisement optimization.

Contextual information optimization: The multi-armed bandit algorithm can also improve the advertising effect by optimizing the contextual information when the advertisement is displayed. For instance, when displaying an advertisement, contextual information such as the scene, time, and geographic location of the user may be considered, and an advertisement content suitable for the context may be selected. By monitoring the correlation between contextual information and advertising effects in real time, it is possible to continuously adjust advertising display strategies, improve the click-through rate, conversion rate and other indicators of advertising, and maximize the benefits of advertising [10].

Personalized pricing strategy: The multi-armed bandit algorithm can also be applied to develop a personalized pricing strategy. By analyzing the market environment, competitors' pricing strategies, and user contextual information, the algorithm can predict the sensitivity of different users to product pricing in different contexts, and flexibly adjust pricing strategies based on this information, thereby increasing sales and profits.

Multi-armed bandit algorithms have broad application potential in the field of content personalization. By utilizing the user's contextual information and personal preferences, the algorithm enables personalized content recommendation and content optimization, thereby improving user satisfaction. Simultaneously, multi-armed bandit algorithm has limitations in recommendation systems. An obvious limitation of the multi-armed bandit algorithm is that each arm must be modeled by a Beta distribution, resulting in binary outcomes of success or failure with every arm trial. Although the multi-armed bandit algorithm can analyze the context information of different environments and recommend relevant content to users, in practical applications, there may be a huge amount of context information in the environment where the recommendation system is located. At this time, the multi-armed bandit algorithm may be used by a large number of interfered by the content of the information, it is impossible to accurately recommend products that fully meet user's favorites to the user in a short period of time. In the future, multi-armed bandit algorithm may be considered for integrating with the neural network algorithms due to their excellent performance in various domains [11, 12].

4. Conclusion

This paper analyzes the application of multi-armed bandit algorithm in the recommended system in recent years and some limitations of itself. At the same time, this article introduces two different algorithms based on the multi-armed bandit algorithm, namely the DC3MAB algorithm and the BiUCB algorithm. This paper also analyzes and summarizes the selection and use of the algorithm which is based on multi-armed bandit algorithm in the recommendation system. After introducing the algorithm process and improvement advantages of the two MAB-based algorithms and comparing them with the basic MAB algorithm, it is more obvious that the two optimization algorithms have better recommendation performance. They can recommend the appropriate content to the corresponding users more accurately and quickly in the recommendation system. Of course, these two algorithms also have a certain degree of limitation in the recommendation system. In the future, it is necessary to further optimize the improved algorithm of MAB for different environments. Through the further optimization of the MAB optimization algorithm, it has more accurate recommendation performance and faster speed of analyzing information in the recommendation system.