Introduction

Over the past several decades, online gaming has become increasingly popular and attracted millions of players all over the world. Moreover, as lucrative commercial value adhered to the games and the player communities were realized, the industry of esports also flourished. Counter-Strike: Global Offensive (CS: GO), for instance, can bring millions of dollars into the prize pool in a single Major-Level tournament. Among various online games, Player-versus-Player (PvP) is a fundamental game mode where players in the games are in direct competition with each other in virtual environments. One of the most well-known genres in PvP is team-based first-person shooters (FPS), where players are divided into teams and typically use weapons such as guns from a first-person perspective to eliminate opponents or complete objectives.

Concerning team-based online games, the quality of matchmaking is strongly related to the player experience in the game and hence has an effect on the life-cycle of games as well. Players are put into an active player pool once they declare their availability for a game, then the matchmaking mechanism can be described as a two-step process: (1) a rating system to evaluate each player in the pool and (2) a matching system to divide them into teams and games. The criteria used to rank each player is critical for a reasonable matchmaking system. One of the conventional widely-used rating criteria is the ELO, where each player’s skill level is independently represented by a single number where only the result of the game (win or lose) is taken into account. However, some may argue that a single number cannot be representative of a player, and criteria including the player’s historical statistics are more convincing than solely the outcome of the game.

To tackle the drawbacks of the traditional ranking systems, the paper has proposed a new skill-based rating system designed specifically for FPS games. The new rating criteria called Skill-Based Individual Player Rating (SBIPR) considers the entire available player profile. From the individual rating, a quantitative measurement, Skill-Based Aggregated Team Rating (SBATR), is defined to rate a team’s skill level. Beyond player and team evaluation, the paper has also developed a definition of fairness of a matchmaking result in team-based games.

Three methods are used to generate global matchmaking results. The methods are tested on an existing dataset and evaluated based on the rating system and the degree of fairness defined in this paper. The paper has investigated the performance of K-means, Balanced K-means Plus Plus (BKPP), and Agglomerative Clustering (AGG). The mechanism using AGG outperforms the other methods regarding the degree of fairness.

The paper contributes to the following aspects:

1. A new metric to evaluate the degree of fairness of a matchmaking result, consisting of a measurement of fairness of a single game as well as two skill-based rating systems for individual players and teams respectively.

2. Demonstrating matchmaking mechanisms based on clustering algorithms and evaluating the performance in the context of skill level and fairness.

The rest of this paper presents the relevant work to this research and discusses the data analysis steps including data preprocessing and feature engineering. Then the paper introduces the definition of fairness, after which the investigations in various clustering models are discussed and results are illustrated. Lastly, the paper discusses potential directions for future work and concludes this paper.

Literature Review

There are some existing rating systems designed for online multiplayer games such as Elo, Glick, and TrueSkill. The Elo rating is specified to calculate relative skill ratings for two-player games; then Glicko extends it with a measure of uncertainty of a player's rating, called rating deviation; after that, TrueSkill uses Glick as the base of the system, where the ratings of players are presented using a normal distribution with two characteristics: mean value to represent perceived skills, and variance to represent how "confident" is the system on the player's mean value [1]. It can be used to predict the probability of a game result, hence making balanced teams from players. As to the updates for skill rating, which depends on the player scoring in a match, RpostA=RprevA+k·(S-E) is used to update, where RpostA represents the upgraded rating and RprevA represents the previous rating before starting the game; k is the weight for the new match; S is the actual result of the game and E is the expected result for the new game [1]. This update can also be explained by the extent of whether the expected outcome and real outcome match.

Another limitation of existing rating systems is that they are uni-dimensional, where a single number is used to represent a player’s rating. However, in team-based FPS games, the skills are evaluated in different aspects such as reflex, ability to read the game and in-team communication, etc. [2]. Therefore a richer player profile and additional contextual information can also be used to predict the game balance rather than relying on a single number [3]. This rating system agrees with the work of [4] which encompasses player skills in multiple facets.

Moreover, the existing rating systems assume that the overall rating of a team is equal to the sum of the ratings of its members, hence every member of a team will get the same update after the game [4]. It also implies each player contributes to the outcome of the game equally. The research of [5] focused on this assumption and turns out there are better options regarding rating a team. The three methods investigated to evaluate a team are MAX, MIN, and SUM. The SUM method is the one used by traditional rating systems, where a team’s rating is the sum of all its members; the MAX method just takes the highest player ratings in the team and implies that a strong player can carry the team to victory; and the MIN method only considers the least skilled member in the team and implies the weak end can drag the entire team down [5]. Based on the results of three settings using traditional ratings (Elo, Glicko, and TrueSkill), it concludes that the MAX method outperforms the other two methods in terms of accuracy in predicting game outcomes [5]. In most scenarios, the MIN method also outperforms the SUM method. This provides evidence against the assumption that all players in a team contribute to the outcome equally and suggests a team’s rating is heavily related to the rating of its best player.

Concerning the concept of matchmaking, one perspective that is often neglected is the difference between local matchmaking and global matchmaking, where the former applies a greedy paradigm to make matches one by one to make sure each game is optimized in terms of fairness given the current status of the player pool. Global matchmaking, on the other hand, focuses on the overall result of all games produced in a player pool [6]. It tends to make a fairer result across all games rather than focusing on making a single fairest game. In this paper, the definition of fairness will be based on global matchmaking.

Research by [7] proposed a balanced K-means method, which means the number of items distributed within clusters is more balanced, providing more equal-sized clusters. When applied to clustering in the game matching, this method could improve the matching results by ensuring the diversity of varied skills of all players in one game. Deshpande et al. [8] discussed the advantage of K-means plus plus in the stability of clustering results regardless of the initial seeds.

Data Analysis

The dataset investigated consists of historical data of more than 2,500 players playing around 170,000 CS: GO games. It contains almost 40 attributes including key performance statistics such as “quantity of kills”, “quantity of death”, “quantity of assists”, “quantity of shots” and “quantity of hits” etc, which are valuable in determining a player’s skill level. The dataset is published in Kaggle at: https://www.kaggle.com/datasets/gamersclub/brazilian-csgo-plataform-dataset-by-gamers-club.

Preprocessing

In its original form, each entry of the dataset represents the statistics of one player in one single game, and the proposed outcome from data processing is to get a dataset such that each entry summarizes the representative historical data of one player.

Before grouping the data together, the unused columns are removed and abnormal data are cleaned. The columns regarding game id, room id, and date created are removed since they are redundant for us to summarize the overall performance of a player. The abnormality check mainly focused on the existence of theoretically impossible data. For instance, a player can only die once in a round, hence an entry is considered erroneous if the number of deaths is greater than the number of rounds in that game. Such entries are removed from the dataset since there is no valid approach to fix them. For the purpose of fairness measuring and model training, a dataset is generated composed of the most recent 100 games of each player.

The data are grouped together by player id to summarize the historical performance of each player. All original attributes are grouped by summation since they are quantities of in-game behaviour which is natural to add up in terms of statistical analysis. Several derived features in the dataset are also calculated by more sophisticated rules, and they will be introduced in the next section.

Feature Engineering

The paper has calculated a few common indicators that are often used to measure a player’s performance:

1. Kill-Death-Assist ratio (KDA): (quantity of kill + quantity of assist) / quantity of death

2. Average Damage per Round (ADR): total damage dealt / total number of rounds

3. Win Rate (WR): number of games won / number of games played

Three key features are also generated based on the FPS game-related knowledge, the following derived features will form the player profile and be used to calculate the skill ratings later:

1. Weighted Hit Rate (WHR): hit rate is adjusted based on the ratio of damages dealt to different parts of the body. It is defined as (0.37 * quantity of hits on head + 0.17 * quantity of hits on chest + 0.16 * quantity of hits on stomach + 0.08 * quantity of hits on left arm + 0.08 * quantity of hits on right arm + 0.07 * quantity of hits on left leg + 0.07 * quantity of hits on right leg) * 7 / quantity of shots

2. Brilliant Performance (BP): average quantity of highlights of a player in a game. It is defined as (0.1 * quantity of 3-kills + 0.15 * quantity of 4-kills + 0.2 * quantity of 5-kills + 0.15 * quantity of first-kill + 0.2 * quantity of headshots + 0.1 * quantity of clutchwon + 0.1 * quantity of flash assists) / number of games played

3. Overall Performance (OP): this feature represents the general skill level of the player and is indicated by the three common indicators: 0.4 * KDA’ + 0.4 * ADR’ + 0.2 * WR’ where’ indicates the relative rank of the attribute. Since KDA, ADR and WR are not on the same scale, the summation is based on the relative rank of each player’s attributes on the entire player population. Note that in real life, the game company has the data of all the players hence the rank on these attributes as well. For the dataset, the paper has used kernel density estimation (KDE) to estimate the underlying distribution of each of the attributes [9]. The paper then replaces the original attribute with its value evaluated in the cumulative density function (CDF), which is used to estimate the relative rank. This paper picked the bandwidth of KDE by Scott’s rule and chose to use the Gaussian kernel function. The implementation of KDE is based on the ‘gaussian_kde’ function from the ‘scipy.stats’ package in Python.

Since clustering techniques require data in all dimensions to be on the same scale, this paper also applied Gaussian KDE to standardise the key features of WHR and BP. Similar to the process on KDA, ADR, and WR, KDE is applied to each key feature respectively to get the estimated distribution and replace the original value by its evaluation in CDF. The bandwidth and kernel function is the same as for generating OP. The Gaussian kernel function is chosen since the attributes are approximately Gaussian distributed as illustrated in the next section.

Data Visualization

As displayed in Figure 1, both KDA and ADR are well-shaped to be estimated by the Gaussian KDE. WR, despite the few extreme values in the two tails, is overall bell-shaped as well. This paper also gives WR the least weight among these three features to lower the effects of the behaviour in the tails.

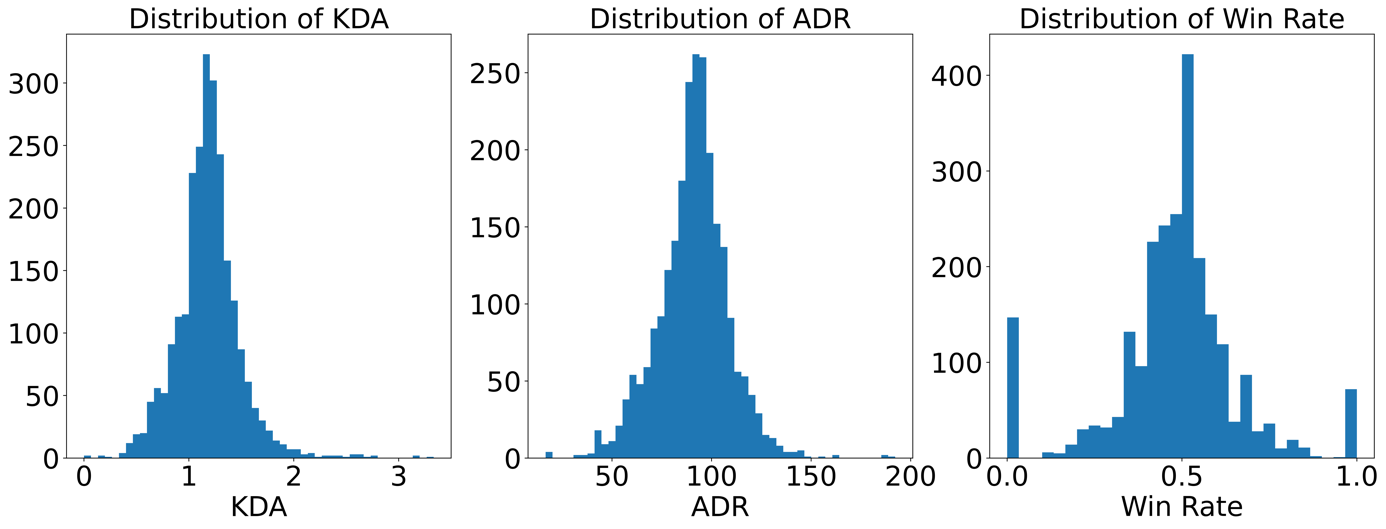
Figure 1. Distribution of KDA, ADR, and WR

In order to evaluate the SBIPR, gaussian KDE is also carried out to standardise the other two key features except for OP: WHR and BP. Figure 2 illustrates that these two derived features are approximately Gaussian distributed as well. Hence it is valid to use the Gaussian kernel function.

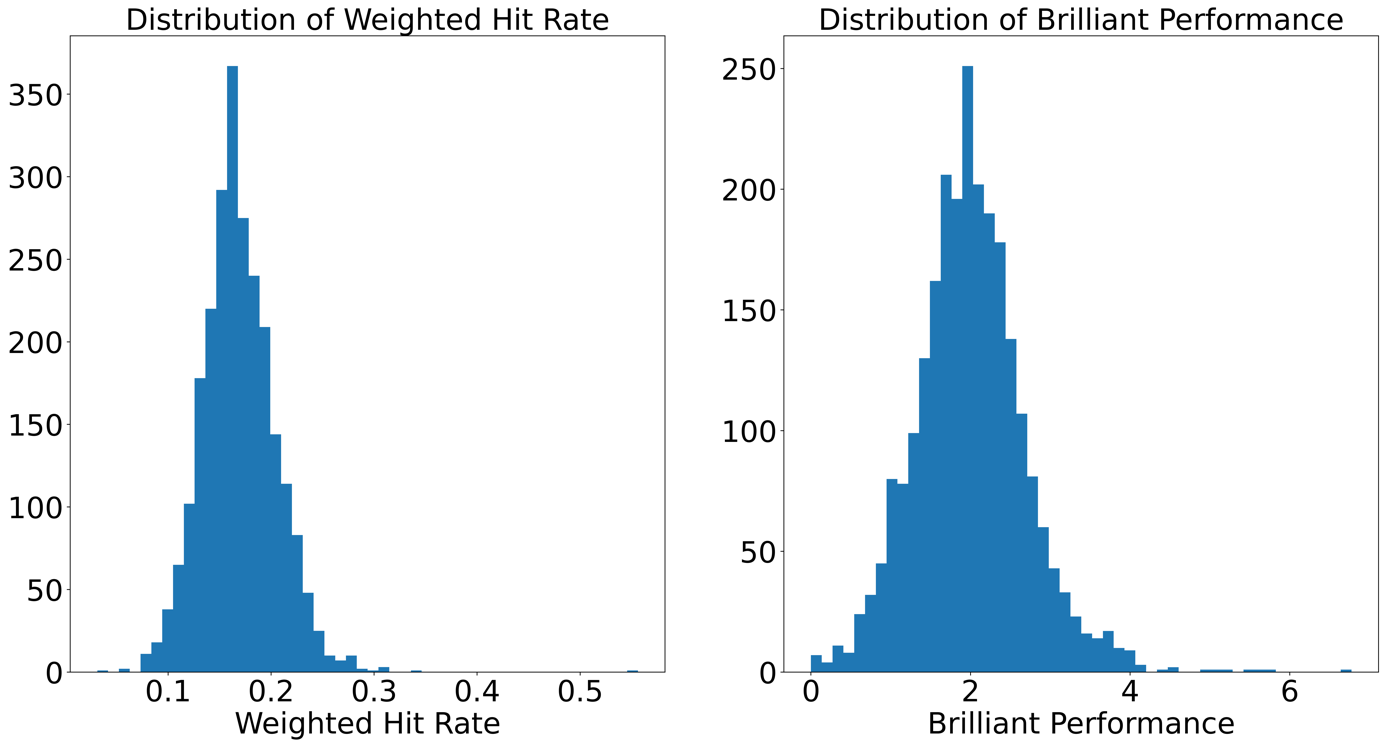
Figure 2. Distribution of HR and BP

Player Grade Labelling

In real life, players achieve different levels in the rank mode. There exists a matchmaking constraint such that players with significant differences in their rank mode cannot be matched together. To mimic this behaviour, players in the dataset are labelled and 7 mutually exclusive player pools are created accordingly. The paper labels the players by explicitly generating their individual player ratings and separates them based on their rank in the ratings. For instance, the A-grade pool contains the top 10% of players while the B-grade pool contains the next 16% of players.

The paper also trained a classifier model based on previous label results. The purpose is to evaluate a player in terms of the grade based on the input features. A variety of methods have been investigated and logistic regression was picked to get a better classification effect.

The paper first standardized the data by normalization: X_scaled = (X - X.mean()) / X.std(). The scaled data is then fitted by overparameterizing the model using K-weight vectors for ease of implementation and to preserve the symmetrical inductive bias regarding the ordering of classes. This effect becomes especially important when using regularization. The choice of overparameterization can be detrimental for unpenalized models since the solution may not be unique. L2 regularization is applied and the following accuracy is achieved:

It can be concluded that the accuracy of predicting grades is higher in the two ends compared to the middle grades. A potential causation is that high-level players tend to have better performance regarding all the features, similarly, bad players tend to suffer in all features. However, average players may be good at some aspects while performing poorly in others, hence they are more difficult to evaluate.

Final dataset

With all the steps described above, a dataset that will be used for the later clustering and matchmaking process is generated. For each player, the dataset contains id, BP, OP, WHR, and a label indicating the grade. The paper uses the grade label to divide the players into separate player pools, and will carry out matchmaking mechanisms based on the three key features.

Fairness Definition

In this section, this paper will introduce a new definition of fairness of a matchmaking result, which consists of skill-based methods to rate a player’s skill level and a team’s skill level. All illustrations are based on the context of the game CS: GO where each game involves two teams and each team has five players, but the idea is adaptable to other FPS games with corresponding adjustments to the key features and weight factors.

This paper defines the problem of matchmaking as the following:

Let \(P\) denotes the player pool that contains all of the active players who are looking for a game. Let \(N\ = \ |P|\) be the number of players in the player pool. Given a specific player pool, the result of a matchmaking result consists of \(N\ /\ 10\) matches, where each match indicates the two teams selected. All the teams are non-overlapping unordered combinations of five players from \(P\).

Skill-Based Individual Player Rating (SBIPR)

Concerning individual player rating, three key performance features are chosen to indicate a player’s skill rating: OP, BP, and WHR. The skill level of a player is determined by a weighted sum of the attributes, where the weight factors are defined empirically based on specific practical knowledge of the game CS: GO and suggestions from experienced players. For later investigation in this paper, the paper applies the following weight factors: OP (50%), BP (35%), and WHR (15%)

Formally, the SBIPR of a player can be calculated as

\[SBIPR\ = \ 0.5\ \cdot \ r_{OP} + 0.35\ \cdot \ r_{BP} + 0.15 \cdot r_{WHR}\ \]

Skill-Based Aggregated Team Rating (SBATR)

Given each player’s SBIPR, a team’s skill level (SBATR) can be determined by a weighted sum of ratings of all its members where the player with the highest rating has the highest weight (35%), the player with the lowest rating holds the second highest weight (20%), and the rest shares a weight of 15% each. Similar to individual player ratings, the weight factors are defined empirically.

Formally, the SBATR of team A, \(R_{A}\), can be calculated as:

\({SBATR}_{A}\ = \ 0.35\ \cdot \ r_{(1)}\ + \ 0.2\ \cdot \ r_{(5)}\ + \ 0.15\ \cdot \ (r_{(2)}\ + \ r_{(3)}\ + \ r_{(4)})\),

where \(r_{(i)}\) is the ranked SBIPR, representing the i-th highest player rating in team A.

The rationale for assigning these weights corresponds to the result that not all the players in the team contribute equally to the outcome of the game. Dehpanah et al. [10] discovered that solely considering the rating of the most skilled player in the team provides a better prediction of the outcome of the game than taking the mean across all players’ ratings in the team. Meanwhile, the study suggests the worst player in the team also affects the overall performance of the team significantly, hence this paper adapts to take all players into account where the most skilled player and least skilled player have larger weight factors.

Skill-Based Game Fairness (SBGF)

Concerning a single game G consisting of team A and team B, the paper defines the degree of fairness of the game, skill-based game fairness (SBGF), to be the absolute difference between those two teams’ SBATR:

\(SBGF_{G}\ = \ \left| {SBATR}_{A}\ - \ SBATR_{B} \right|\),

where \(R_{A}\) and \(R_{B}\) are calculated in the section above.

Skill-Based Global Matchmaking Fairness (SBGMF)

For a global matchmaking M that matches a total of N games for all players in \(P\), the degree of fairness, skill-based global matchmaking fairness (SBGMF), is defined as the maximum absolute difference over all the games matched:

\[{SBGMF}_{M}\ = \ \max({SBGF}_{i}),\ i\ = \ 1\ to\ N\]

where i is the index of the game made in the matchmaking.

The degree of fairness of global matchmaking is indicated by SBGMF, since this paper treats the maximum absolute difference as the upper bound of the degree of unfairness, and evaluates various matchmaking mechanisms based on this metric. In the result section, the thesis also investigates the mean of SBGFs in a global matchmaking result to fulfil a thorough analysis.

Methodology

Since the definition of fairness is defined as closed forms, there exists an analytical optimal global matchmaking for each player pool. However, this would require traversing all possible combinations and is not practically possible as the size of play pools increases. The paper presents three methods to mimic a matchmaking system: K-means, agglomerative clustering (AGG), and Balanced K-means ++ (BKPP). All three methods are based on the principle of clustering to divide players into different groups of 10, where each group represents a game. Since clustering cannot guarantee that each cluster contains exactly 10 points, each method consists of two steps: (1) Traditional Clustering and (2) Cluster Transfer. After the players are divided into groups of 10, for each group we consider all 252 (10C5) possibilities of assigning teams. The SBGF is evaluated on each assignment and we pick the optimum one for each game (i.e., team assignment results in minimum SBGF).

K-means

The K-means method uses the standard K-means algorithm for the first step. The algorithm is implemented by the ‘KMeans’ function from the ‘Sklearn’ Package. Due to the nature of the matchmaking problem, the number of clusters, K, has to be N / 10 in our implementation. In the second step, the paper transfers data points in overfull clusters one by one. For each cluster that contains more than 10 points, the paper locates the point that is furthest from the centroid and moves it to the nearest underfilled cluster.

Balanced K-means Plus Plus (BKPP)

The BKPP method implements the first step by an adapted K-means called Balanced K-means Plus Plus. Again, K is N / 10. It initializes the first centroid randomly and explicitly calculates the other centroids to ensure a more stable result. It also takes the diversity of points into account (i.e., affinity to points with different values in one dimension, yet have close overall ratings). The transferring step in BKPP is similar to the process in K-means.

Agglomerative Clustering (AGG)

In the first step, the AGG method uses an agglomerative clustering method based on the ‘AgglomerativeClustering’ function in the ‘Sklearn’ package. The number of clusters is set to N / 10. To ensure each cluster contains exactly the number of points required, they are reassigned randomly from overfull clusters to underfilled clusters in the transfer step.

Wave Algorithm

A new algorithm called “Wave Algorithm” is proposed for cluster transferring to ensure each cluster contains exactly the same number of points. Points are moved one by one from the cluster with the most points to the cluster with the least points, where potential intermediate clusters are determined to diminish the effect of transferring clusters. This prevents clusters from receiving a point that is far from their original centers. The input of the algorithm requires the target size (which is always 10 in our scenario), cluster sizes, cluster centers and the labelling results. The implementation of the algorithm is described below:

Algorithm WaveAlgorithm(clusterSize, clusterCenter, clusterData, target-

Size)

Function distance(point a, point b)

return norm(a-b)

End function

Function transferCluster(cluster index A, cluster index B)

BCenter = clusterCenter[B]

t = the minimum point with label A that is closet to BCenter

clusterData[t] = B

recalculate and update clusterCenter[A]

clusterSize[A] -= 1

recalculate and update clusterCenter[B]

clusterSize[B] += 1

End function

maxClusterDize = max(clusterSize)

if maxClusterSize ! = targetSize then

1. = cluster index with largest size

2. = cluster index with smallest size

ACenter = clusterCenter[A]

BCenter = clusterCenter[B]

potentialIntermediateClusters = []

for all clusters C except A and B do

CCenter = clusterCenter[C]

if distance(ACenter, CCenter) < distance(ACenter, BCenter) and

distance(BCenter, CCenter) < distance(ACenter, BCenter) then

potentialIntermediateClusters.append(C)

end if

if potentialIntermediateClusters is empty then

transferClusters(A,B)

else minDistance = positive infinity

for all clusters C in potentialIntermediateClusters do

CCenter = clusterCenter[C]

CDistance = distance(ACenter, CCenter) + distance(BCenter, CCenter)

if CDistance < minDistance then

minDistance = CDistance

intermeidateCluster = C

end if

end for

transferCluster(A, intermeidateCluster)

transferCluster(intermeidateCluster, B)

end if

end for

end if

Grade Pool

In section 3.4, the entire dataset is divided into seven mutually exclusive player pools. Figure 3 indicates the distribution of SBGMF in each player pool is roughly identical by randomly assigning the matchmaking, hence the paper focuses on a single pool to investigate the methods discussed above. In the results section, all results are based on applying the methods to the players in the C-grade pool, which contains almost 400 players.

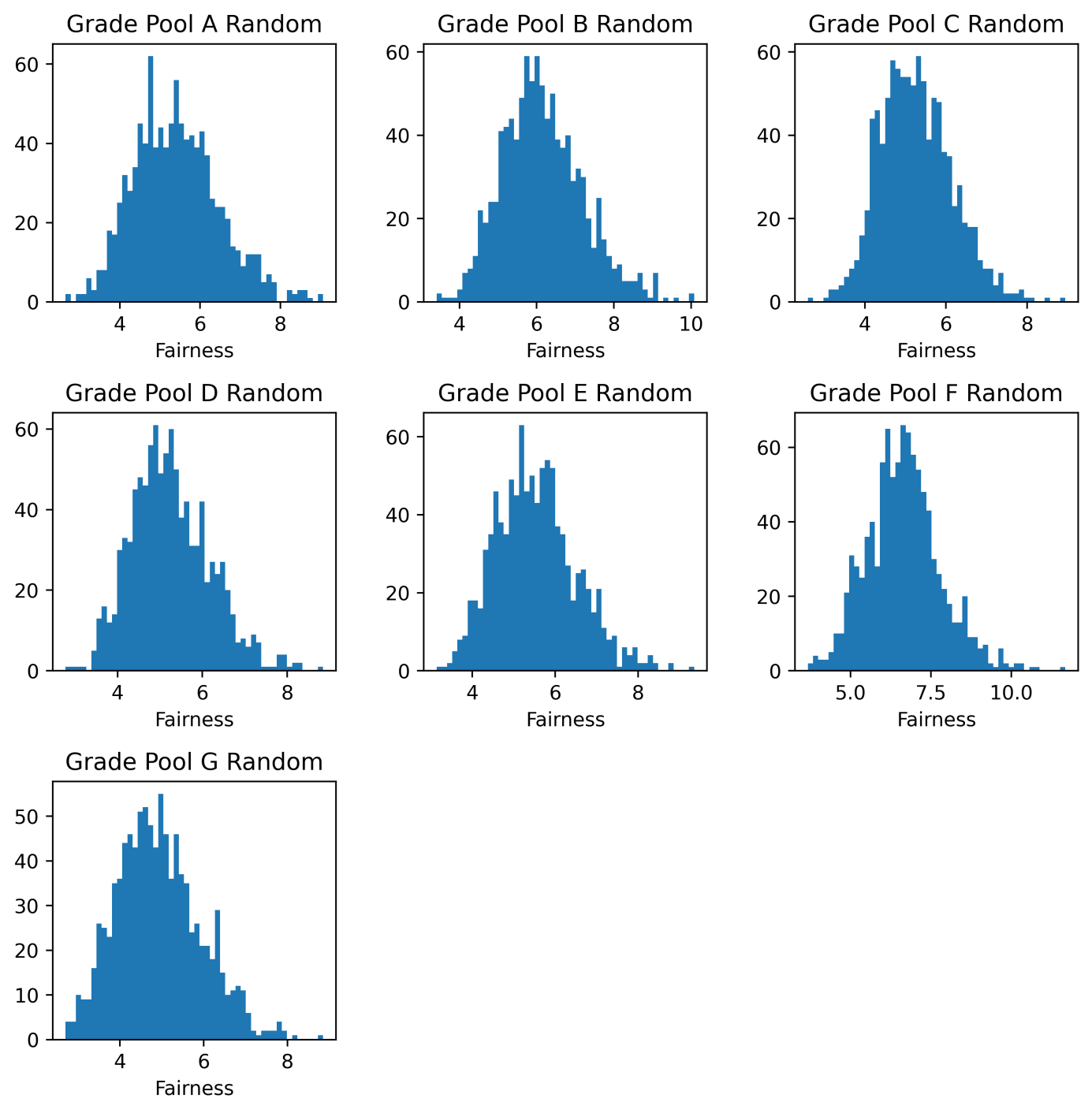
Figure 3. Distribution of SBGMF from random matchmaking in different player pools

Repetitions

Since clustering is not a stable algorithm, the paper picked the appropriate number of repetitions by peeking at the results of repeating the K-means methods at different times.

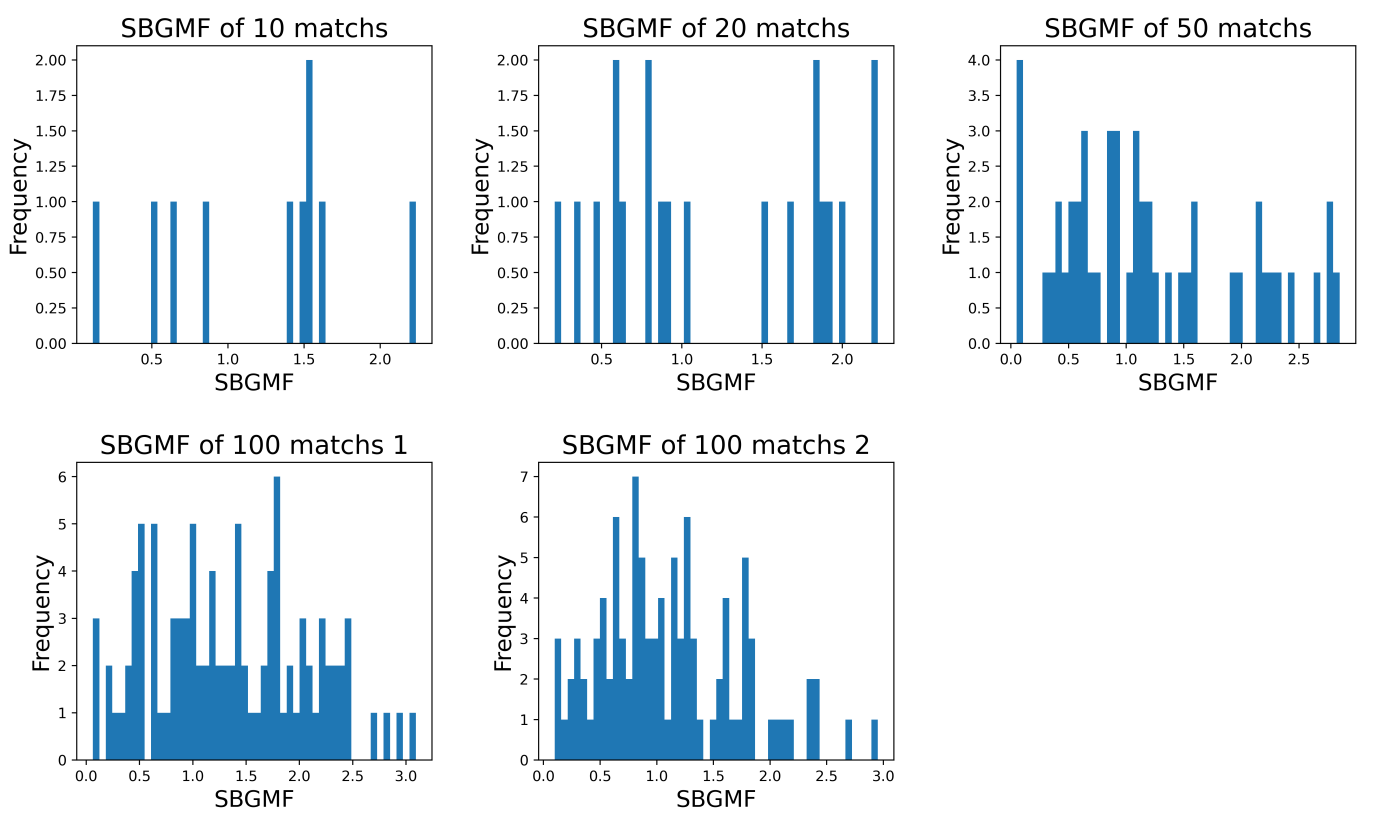
Figure 4. Distribution of SBGMF with different times of repetitions

If K-means is repeated 10 and 20 times, the maximum SBGMF is less than 2, however, when the number of repetitions reaches 50, the maximum SBGMF tends to converge at around 2.5.

Therefore the paper repeats 100 times for each method and analyzes the degree of fairness based on the distribution of several attributes of the 100 matchmaking results.

Result and Discussion

Following the proposal discussed in section 5, the results of each method by carrying out matchmaking 100 times on the C-grade player pool have been generated.

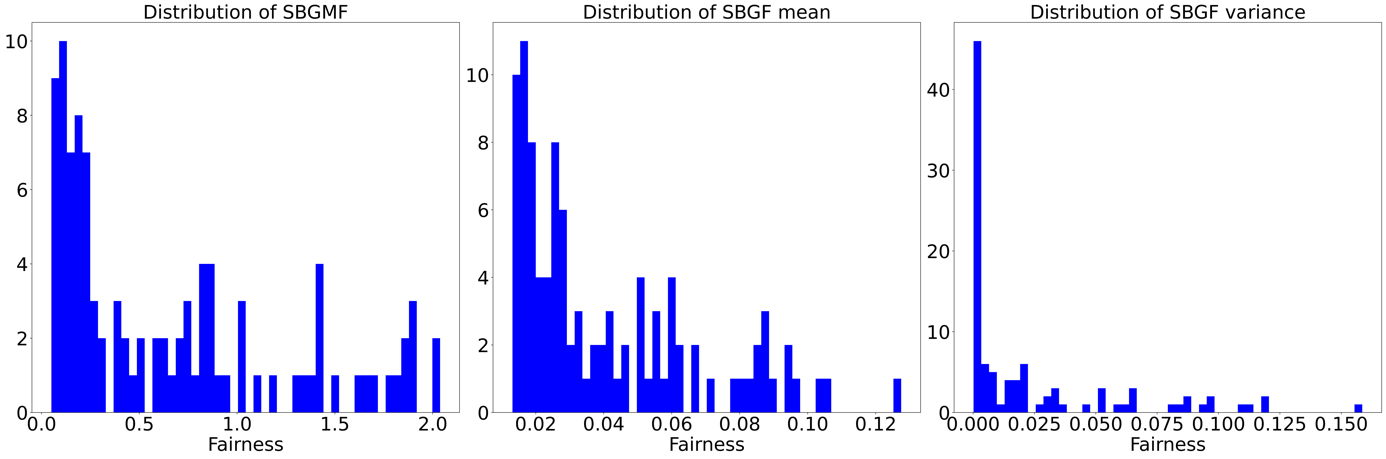
Figure 5. Distribution of results of K-means

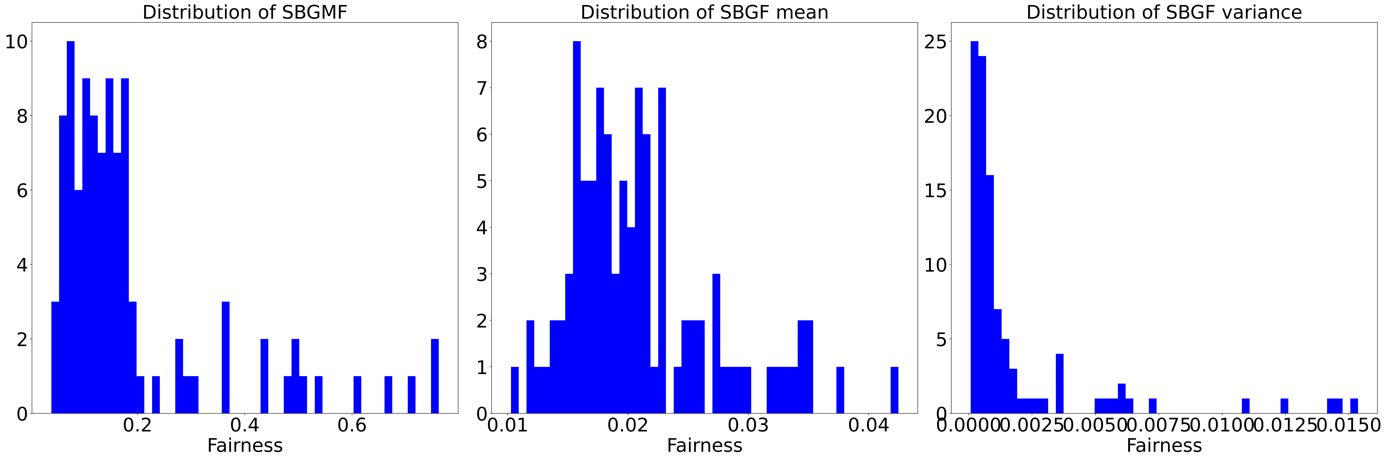
Figure 6. Distribution of results of AGG

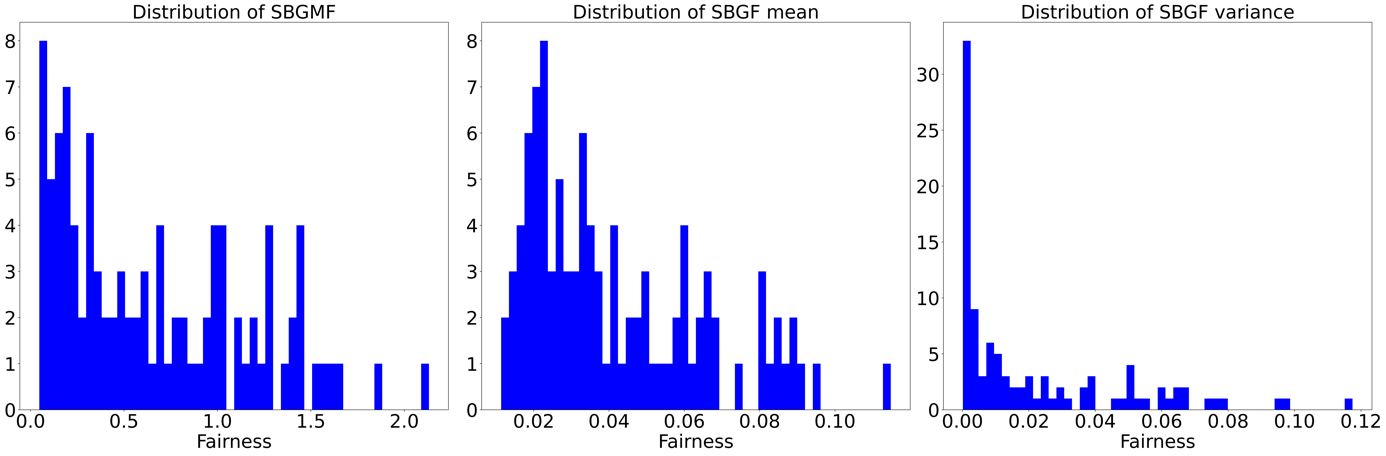
Figure 7. Distribution of results of BKPP

The above three figures display the distributions of SBGMF, SBGF mean, and SBGF variance respectively of each method. Suppose there are n games in one global matchmaking, then there are n SBGF measures. The SBGF mean is the mean of those n measures, similarly, the SBGF variance is the corresponding variance. Although the degree of fairness is determined by SBGMF (maximum of SBGF) based on our definition, the paper displays the average SBGF to illustrate the difference between the three methods as the mean value can provide a different aspect from the maximum value.

Pairwise Comparison

Next, the paper will illustrate the pairwise differences in terms of quantile-quantile plots (QQ-plot).

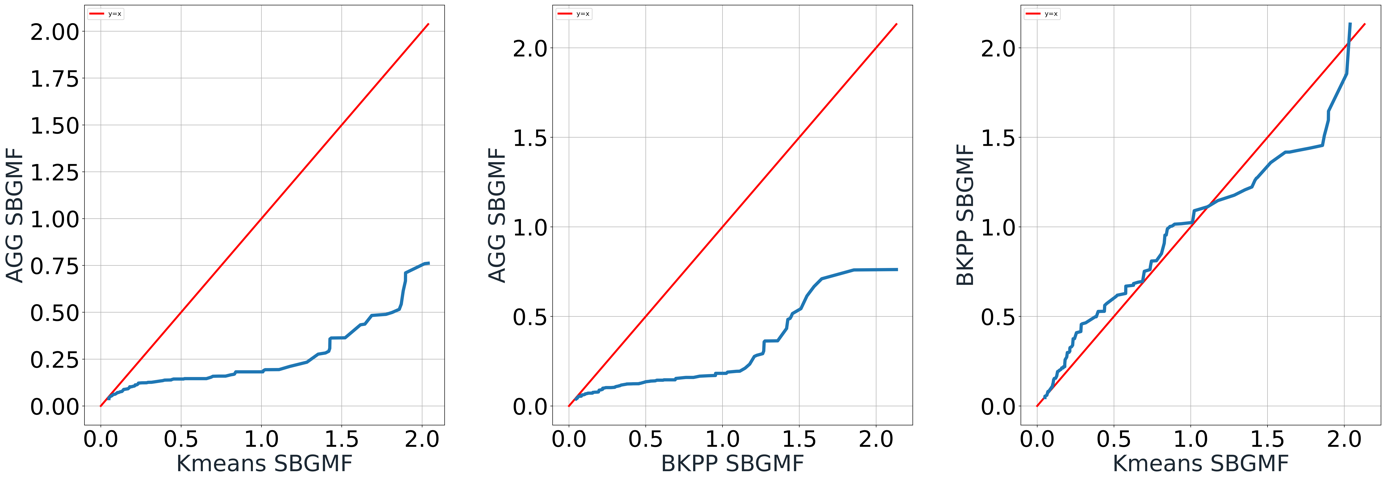
Figure 8. Pair-wise QQ-plot of SBGMF

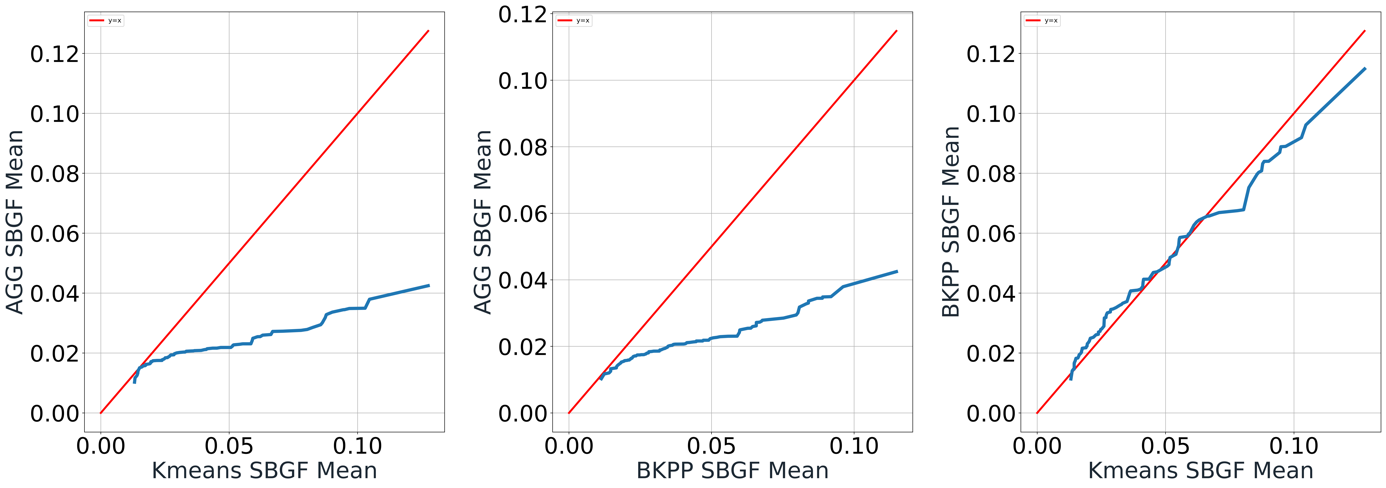
Figure 9. Pair-wise QQ-plot of SBGF Mean

Concerning SBGMF, Figure 8 shows AGG has significantly lower values compared to both K-means and BKPP, which means it produces the fairest matchmaking based on the definitions. The difference is negligible between Kmeans and BKPP. As for SBGF mean, a similar pattern is observed in Figure 9. This concludes that AGG outperforms the other two methods in both SBGMF and SBGF mean. Having a smaller SBGF mean also emphasizes that AGG not only produces the fairest global matchmaking but also makes fairer games in general.

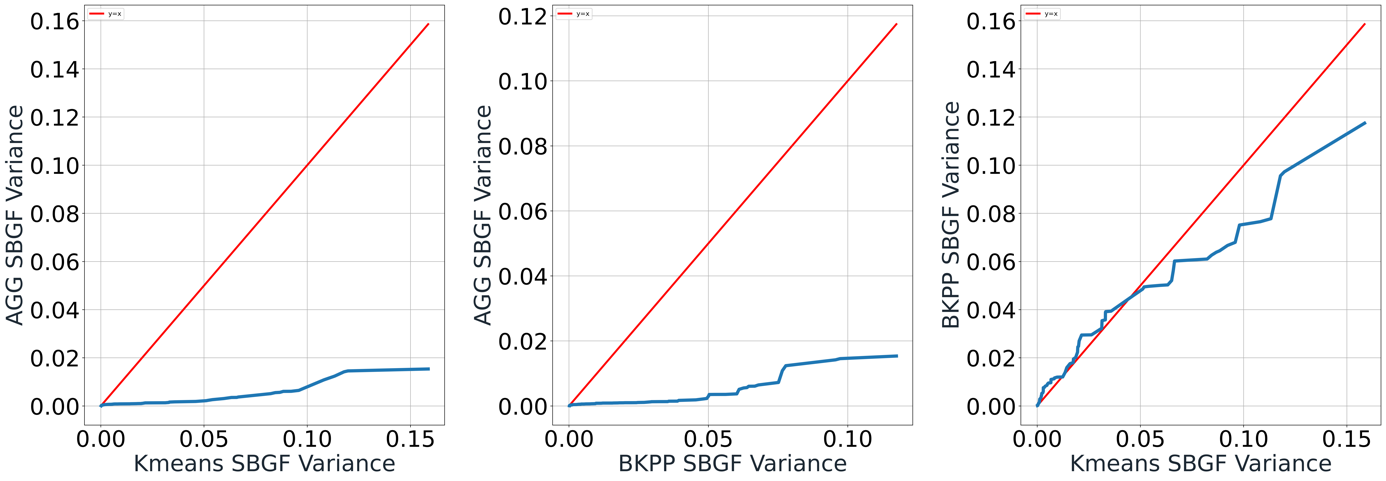
Figure 10. Pair-wise QQ-plot of SBGF Variance

In Figure 10, it matches the expectation that AGG has the smallest SBGF variance compared to the other two methods since both the range and the average of SBGF from AGG are smaller. This indicates that AGG is also more stable in terms of global matchmaking. Focusing on K-means and BKPP, K-means has a smaller variance between the range 0.02 to 0.07, but the pattern reverses for large values of variance. This indicates that BKPP is more stable in worse cases than K-means.

SBGMF Attributes Comparison

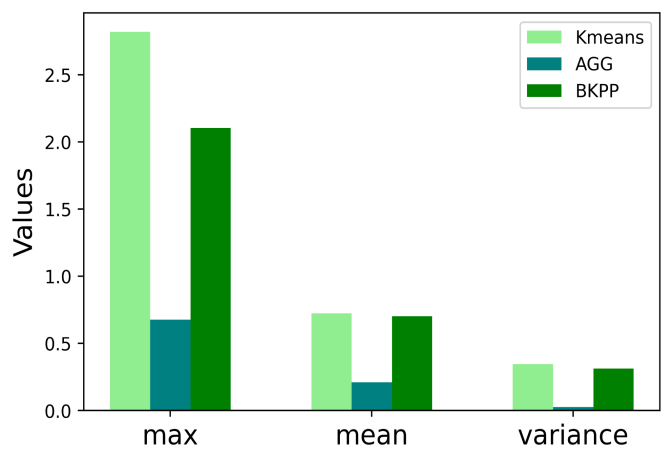
Figure 11. Bar Chart of attributes of SBGMF in Each Method

Figure 11. illustrates the three attributes of the 100 SBGMF produced: maximum, mean, and variance. In agreement with the pattern spotted in the pairwise comparison, AGG outperforms the other methods in all attributes. Therefore, based on the definition of matchmaking fairness, the paper concludes that AGG produces the fairest matchmaking. The low values in mean and variance also suggest AGG is more stable and can produce fairer games in general.

Effectiveness of Wave Algorithm

In this section, the effect of applying the wave algorithms to K-means and BKPP compared to the direct transferring method is illustrated. Since the improvement is relatively insignificant, a data size of 1000 is used for preciseness.

For K-means, Figure 12. shows an improvement in SBGMF, and the mean and the variance of SBGF.

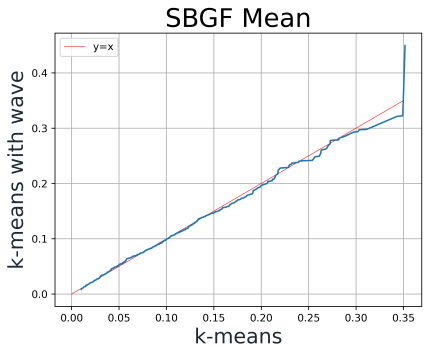
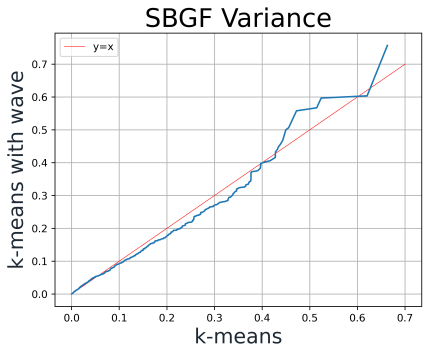
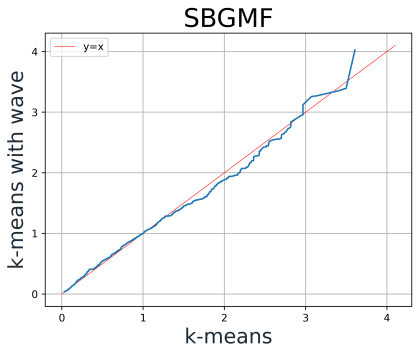
Figure 12. QQ-Plot of K-means AF mean, AF variance and GF value with and without Wave-Algorithm

On the other hand, as shown in Figure 13., the Wave Algorithm negatively influences BKPP. One potential reason is that applying this wave transferring undermines the “Balanced” characteristic of BKPP.

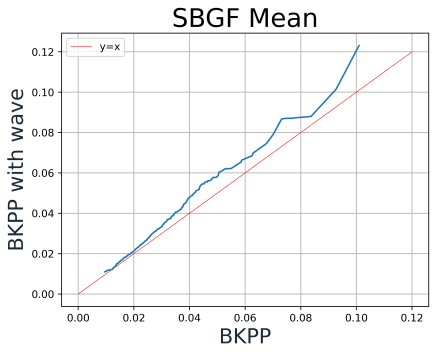
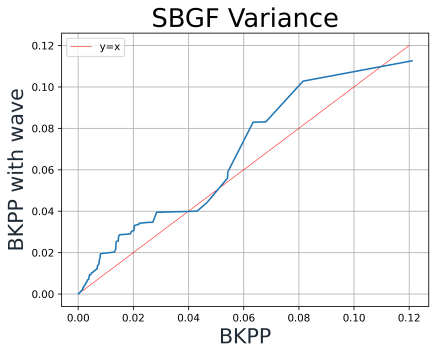
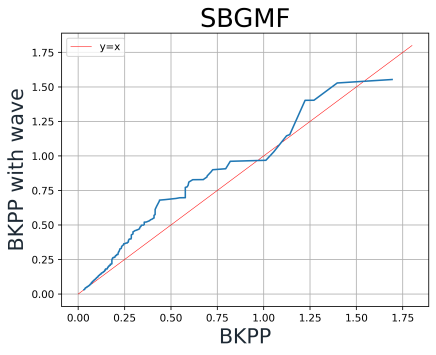
Figure 13. QQ-Plot of BKPP AF mean, AF variance and GF value with and without Wave-Algorithm

Conclusion

In this paper, a new system is defined to rate both individual players and teams in FPS games based on skill levels derived from player profiles rather than ratings adapted to the outcome of the games, from which the paper further defines a metric to measure the degree of fairness of individual games as well as global matchmaking results. The paper also proposed three methods to generate matchmaking results and investigated their performance based on the new definition. All methods use the clustering method as a foundation, and apply certain cluster transfer algorithms to obtain the global matchmaking result. The thesis tested their performance on a real-world dataset for the popular FPS game, CS: GO. The AGG method which uses agglomerative clustering and random clustering transfers produces the fairest matchmaking result.

The thesis also suggests a few potential directions for future research based on the work of this paper. In agreeing to the proposed rating systems and definition of fairness, one can investigate other methods to produce the matchmaking result. For instance, a more robust algorithm to ensure each cluster contains exactly 10 players. Similar ideas of the skill-based definition of fairness and evaluation of players or teams can also be applied to other types of games besides FPS. Lastly, from a practical angle, one can apply the solution in this paper to real life and receive feedback from real players and game companies.