1.Introduction
In the contemporary machine learning training process, the training datasets are typically divided into several batches, with models being updated incrementally through batch-by-batch iterations. Training models in this way not only saves the memory usage but also reduces the risk of overfitting. However, the determination of optimal batch size and the number of epochs lacks a definitive formula or algorithm. These hyperparameters are typically established based on practitioners’ experiential insights. Setting those hyperparameters incorrectly can greatly impact the performance of models. An excessively large batch size might lead to overfitting, whereas an overly diminutive batch size could result in adding noise. In terms of number of epochs, training model after converging is doing nothing but adding noise to the model.
Numerous studies have been implemented to study this problem. They found that errors evaluated by validation set first decreases but followed by an increase as the model starts to become overfitted [1]. To decrease the noise added by over training, many methods are developed to adjust the gradient for each update including AdaGrad which updates frequently occurring features less [2], AdaDelta which extends AdaGrad [3]. Though these methods can optimize the training process in many cases, they are still not perfect solutions. For example, AdaGrad works well only under certain hyperparameters which require manual selection and its learning rate is always decaying throughout training. These makes AdaGrad cannot be widely adapted in every model training. AdaDelta follows main ideas in AdaGrad but makes some modification to ensure that model can keep improving after a great number of training iterations. But its effect is not as good as AdaGrad.
The process of training by batches can be considered as moving a point towards a set of fixed points in space. The fixed points in the set are the models which best fit the data in the batch and the point to be moved is model being trained. Each training iteration can be considered as picking one fixed point from set and move point towards it. The length of each move depends on learning rate and the distance between two points. In this case, the probability of the angle between two vectors from the point to two fixed pointed picked from the set is larger than 180 degrees can also be used to detect the location of the point. When a point is distant from the set, its probability approaches 0. Conversely, when the point lies within the set, its probability is between 0 and 0.5. The closer the point to the mass center of the point set, the closer the probability is to 0.5. This paper aims to find a superior new method to optimize training process based on that probability.
The rest of this paper will be organized as follow: Section 2 provides a discussion of the theory behind the proposed method, the dataset used, the model structure and the experiment details. Section 3 provides a discussion of the experiment result and some possible reasons behind it. The conclusion and future work are discussed in Section 4.
2.Method
There will be two experiments in this paper. The first one is a simple Deep Neural Network trained on MNIST dataset [4] and the second one is ResNet18 [5] trained on CIFAR-10 dataset [6].
2.1.Dataset preparation
MNIST dataset contains grey-scale images of 32×32 handwritten digits from United States Census Bureau employees and high school students with 60,000 training data and 10,000 testing data. Each image in MNIST is size-normalized and centred in a 28×28 image [6]. Some sample images on the MNIST dataset are provided in Figure 1.
|
|
|
Figure 1. Sample images in the MNIST dataset [4]. |
CIFAR-10 dataset contains RGB images of 10 mutually exclusive classes. Each class has 5, 000 training and 1, 000 testing data. Each image is 32×32 and contains exactly one object belongs to its class [4]. Some sample images on the CIFAR-10 dataset are provided in Figure 2.
|
|
|
Figure 2. Sample images in the CIFAR-10 dataset [6]. |
2.2.Model description
The model trained in the first experiment will be a DNN with only 3 full connected layers, with ReLU employed as the activation function. To train this model, the image is first flattened to a 1-d tensor with 784 entries and input to first fc layer. The first fully connected layer transmits 500 parameters to the second layer and the second layer transmits 200 parameters to the third layer. The third layer returns 10 parameters which is probability of the class the input image belonging to.
The model trained in the second experiment will be ResNet-18. It is an 18-layer ResNet based on Convolutional Neural Network. At the heart of ResNet lies the fundamental concept of enabling its layers to adapt to a residual mapping rather than a direct underlying mapping, thereby allowing for the potential of updates to bypass multiple layers during training. ResNet18 is designed for ImageNet dataset, so its last fully connected layer outputs 1000 features. But CIFAR-10 only has 10 labels. Therefore, the original output layer in ResNet18 is replaced by a fully connected layer outputing 10 features.
2.3.Proposed AdaGCR
In 2-D space, the location of a point in a set of fixed points can be inferred from its probability of picking two points that are in the opposite direction (dot product of the vectors from unfixed point to fixed point is less than 0).
|
|
|
(a) Probability of a uniformly distributed point set. |
|
|
|
(b) Probability of a point set with more points distributed on top-right corner. |
|
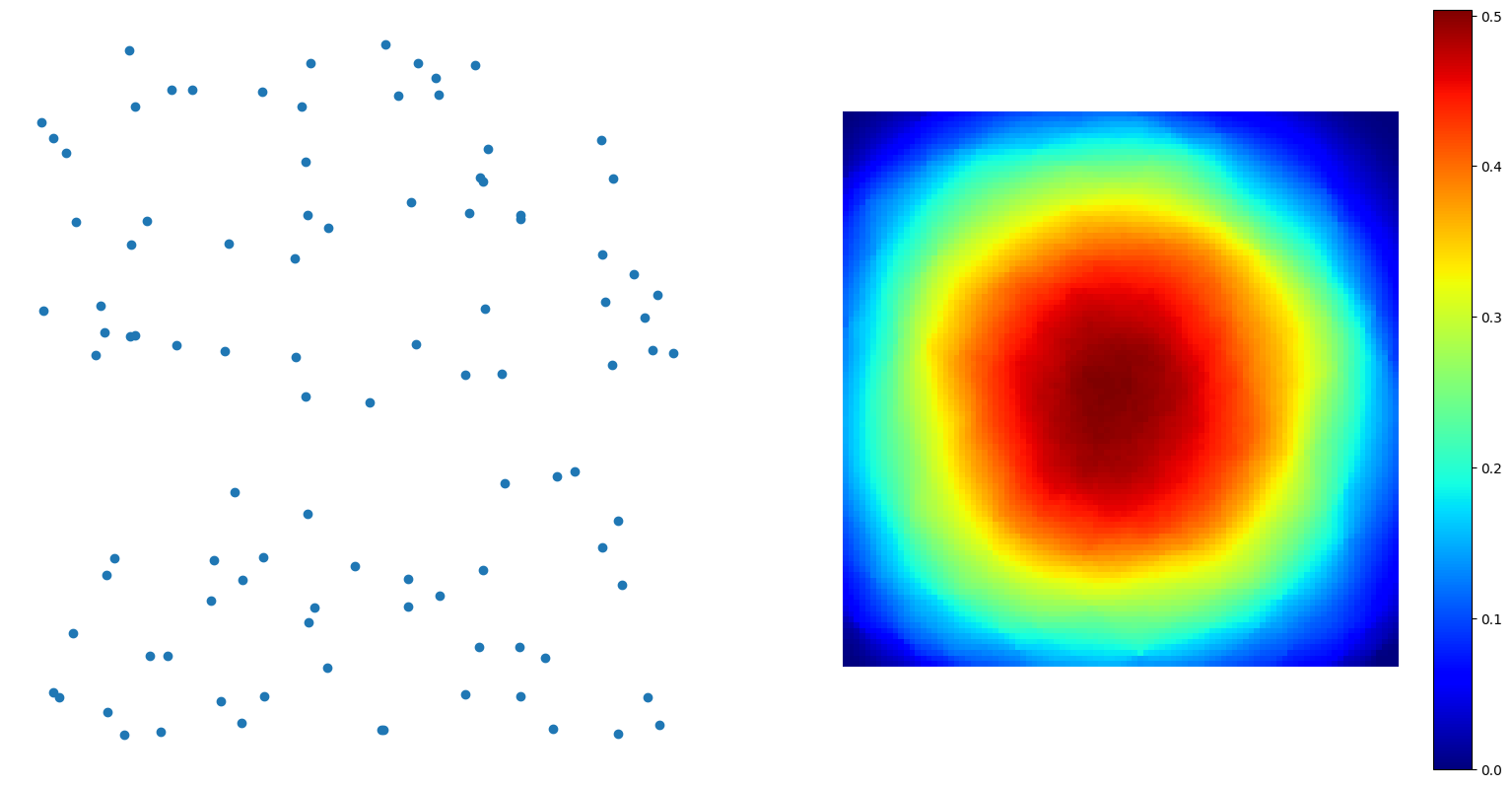
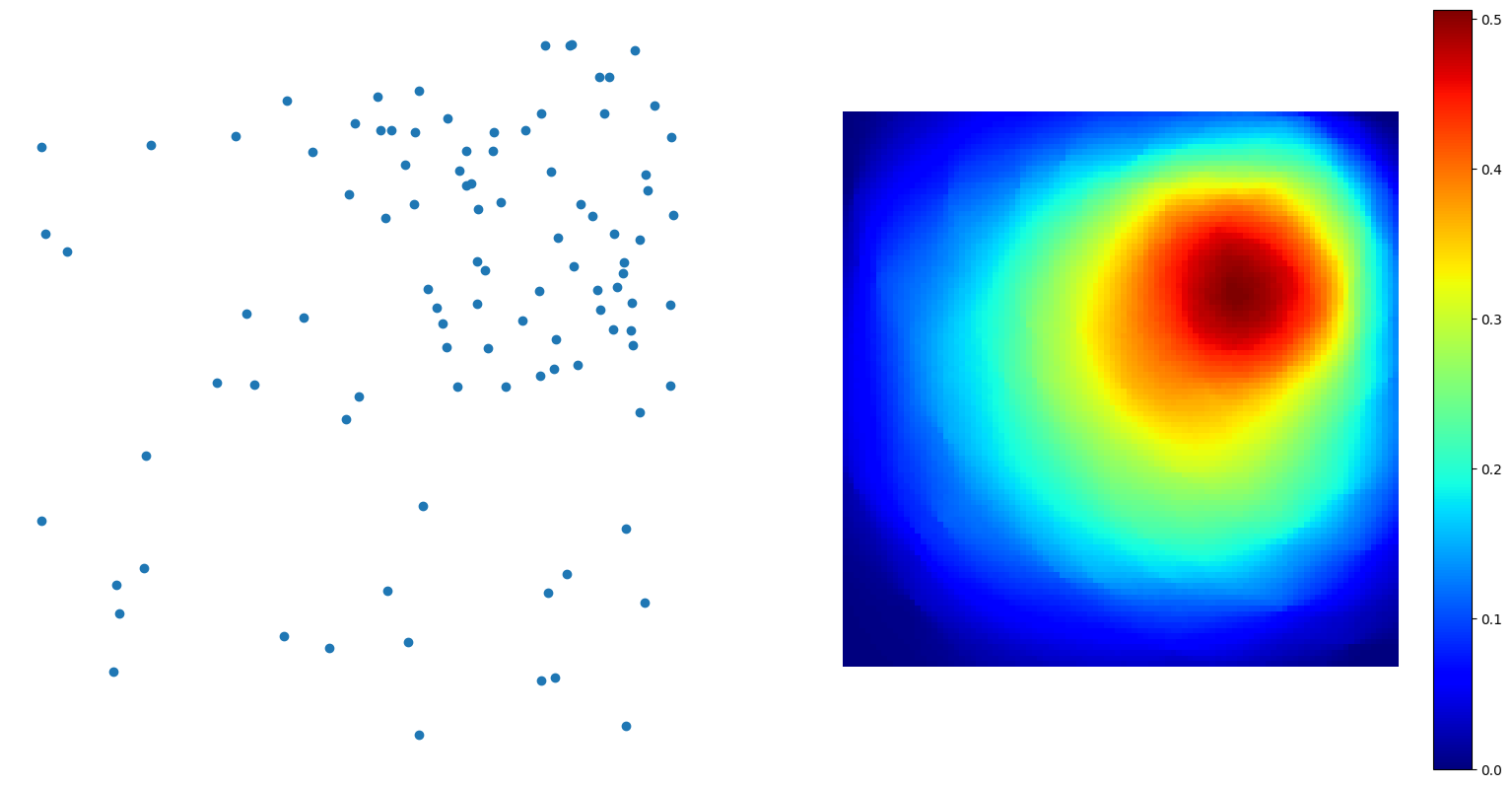
Figure 3. Probability of picking two points in the set that are in the opposite direction (Photo/Picture credit: Original). |
According to Figure 3, the closer the point is to the mass center of the point set, the closer its probability of picking two points that are in the opposite direction is to 0.5. This idea does not work perfectly for a dynamic system like updating model in machine learning. But the “gradient conflict rate” — the ratio of how many iteration whose updating gradient is opposite to last iteration’s updating gradient to the number of iteration in one epoch will increase as model approaches the mass center of batch models. And if learning rate is equal to 0, the gradient conflict rate will be equal to the probability of picking two points in the set that are in the opposite direction. By multiplying the learning rate with a decay function, the gradient conflict rate can be a good approximation of the probability when model is close to the mass center.
|
|
|
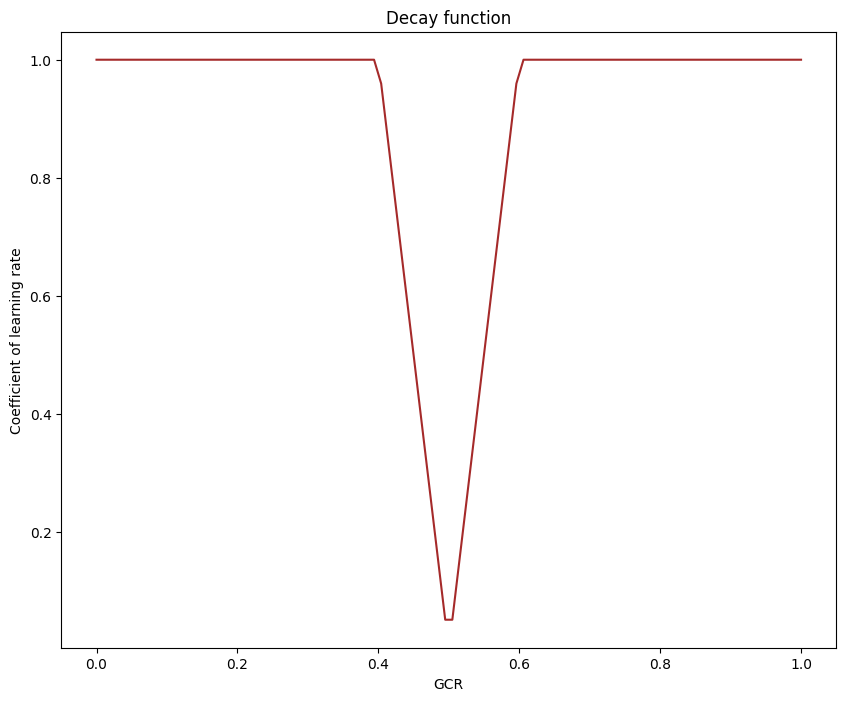
Figure 4. Decay function (Photo/Picture credit: Original). |
Therefore, the gradient conflict rate can reflect each epoch’s updating status. If the model after this epoch’s updating is still very far from the goal, then its gradient conflict rate for this epoch should be zero. Since the product of decay function shown in Figure 4 and learning rate is approaching 0 when gradient conflict rate is approaching 0.5, the model should move slightly around batch models’ mass center after adequate training epochs. In this case, further training will not significantly change model’s location. This new proposed optimizing method is named as “AdaGCR” which stands for Adaptive Gradient Conflict Rate.
2.4.Implementation details
The machine learning framework used in this paper is pytorch. The proposed method is based on SGD [7]. Its implementation is calculating the gradient conflict rate after one epoch’s training, then use that value and decay function to adjust global learning rate.
In terms of the first experiment, the proposed new method is compared with SGD without any optimizer as baseline, AdaGrad [8] and AdaDelta [9]. The loss function employed is cross entropy loss. The experiments are conducted under several pairs of learning rate and batch size.
The second experiment is similar to the first one except the model is ResNet-18 and the dataset is CIFAR-10. This experiment aims to test proposed method on more complex model designed for solving real world problems. The batch size is set to be 256 and the learning rate is set to be 0.1.
3.Results and discussion
3.1.Testing proposed method on DNN models trained by MNIST
|
|
|
|
|
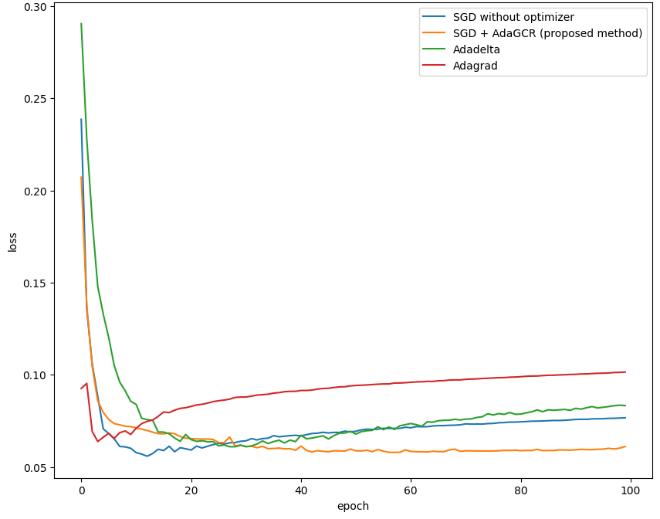
lr = 0.01, batch_size = 32. |
lr = 0.01, batch_size = 32. |
|
|
|
|
|
|
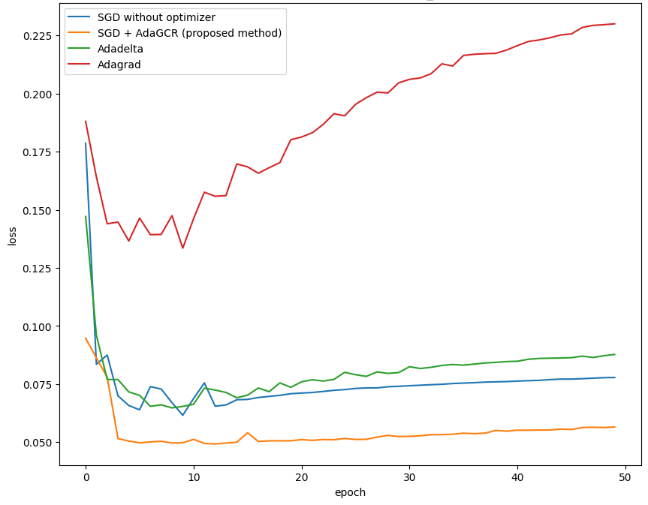
lr = 0.2, batch_size = 32. |
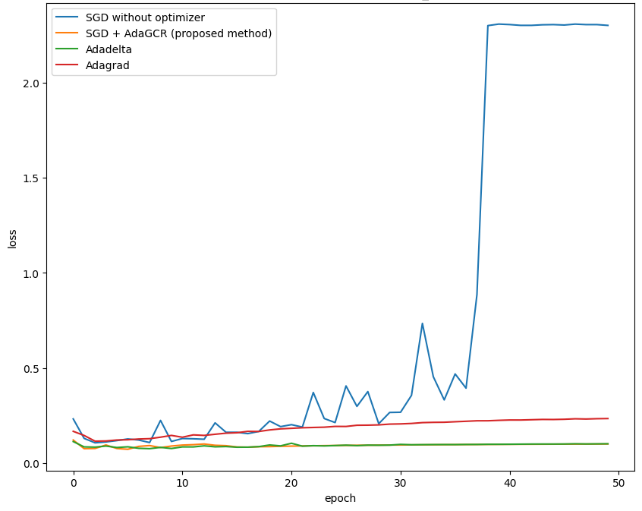
lr = 0.2, batch_size = 8. |
|
|
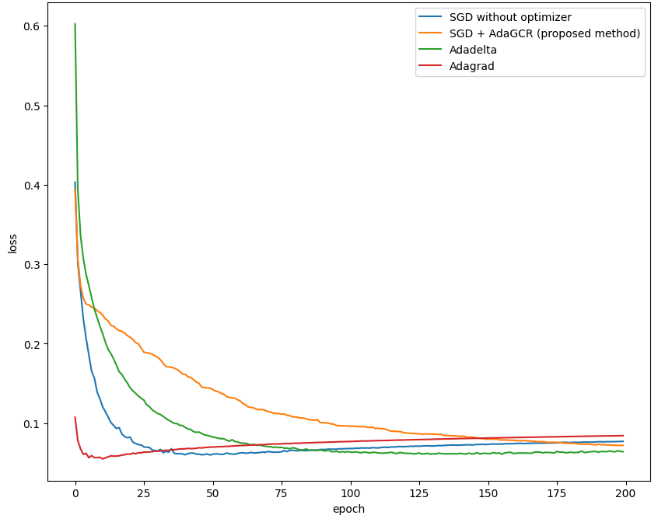
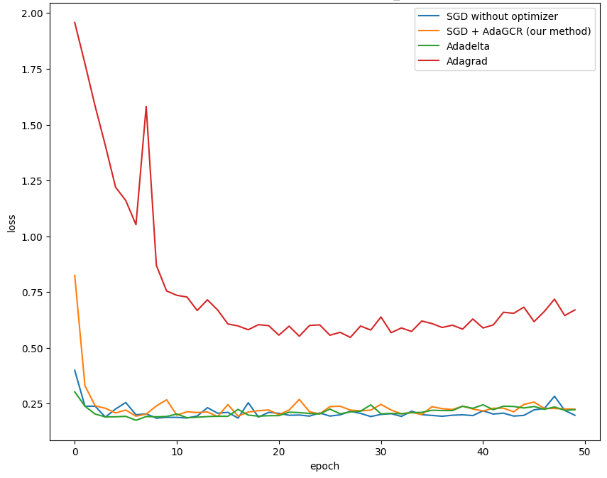
Figure 5. The loss of test dataset from DNN model trained by MNIST dataset (Photo/Picture credit: Original). |
||
Figure 5 presents the loss of test dataset from DNN model trained by MNIST dataset. The method under consideration has been evaluated across various combinations of hyperparameters. Its fundamental concept involves decreasing the learning rate as the model approaches the desired outcome. Consequently, this approach performs optimally with a higher initial global learning rate. Specifically, when the batch size is set at 32 and the learning rate is 0.2, the proposed method outperforms both AdaGrad and AdaDelta. However, when the learning rate is reduced to relatively lower values such as 0.05 and 0.01, the proposed method results in a slower model convergence. It can also be observed that the proposed method reduces the effect of overfitting after several epochs’ training. When batch size is small (batch size = 8), using SGD cannot make the model converging. But the proposed method can solve this problem and it performs as good as AdaDelta. This is because the proposed method detects model’s location and adjust learning rate only according to the distribution of point. In this case, the number of points does not significantly affect the result.
3.2.Testing proposed method on ResNet18 trained by CIFAR10
|
|
|
|
|
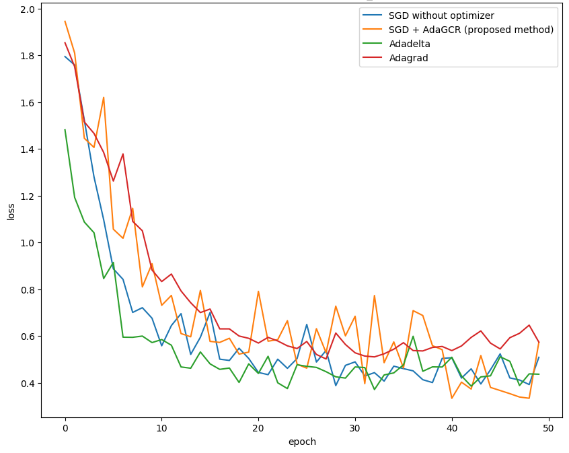
lr = 0.5, batch_size = 256 |
lr = 0.1, batch_size = 256 |
|
|
Figure 6. The loss of test dataset from ResNet18 model trained by CIFAR10 dataset (Photo/Picture credit: Original). |
||
The proposed method is tested under different hyperparameters. But according to Figure 6, its result on ResNet18 does not have a significant improvement compared with AdaGrad, AdaDelta and baseline SGD. The performance of model trained by the proposed method is better than the performance of model trained by AdaGrad but similar to the performance of model trained by baseline and AdaDelta.
The observed phenomenon can be attributed to the intricate architecture of ResNet18. ResNet comprises both fully connected and convolutional layers, each with distinct weight structures. However, in the methodology presented in this paper, all weights are flattened when computing the gradient. A potential avenue for future research is to compute the gradient conflict ratio on a per-layer basis and subsequently adapt the learning rate for each layer accordingly. Moreover, because the idea behind gradient conflict rate is sample proportion, there should be enough batches in one epoch and the batch size cannot be set too large. According to the experiments in this paper, one epoch should have at least 500 batches. Otherwise, the gradient conflict rate will lose accuracy and become meaningless. Additionally, the proposed method can be also considered for combining with the non-IID issue in heterogeneous federated learning [10] in the future.
4.Conclusion
In this paper, a novel optimization method rooted in SGD is introduced for learning rate adjustment. This method is tailored to enhance the training process in machine learning by considering the gradient conflict rate, which provides insight into the model’s positioning within each batch. Experimental evaluation across two distinct tasks reveals its potential in mitigating overfitting and enhancing convergence. Notably, it demonstrates significant benefits when applied to simpler DNN models, especially when paired with a well-chosen initial learning rate. However, its effectiveness may be limited when dealing with more complex models like ResNet-18, which may require more sophisticated adaptations to accommodate their intricate architecture. Further research and experimentation like adjusting learning rate by layers are needed to fine-tune the proposed method and explore its applicability to a wider range of machine learning models and tasks.
References
[1]. Bishop C M 2006 Pattern recognition and machine learning Springer New York p 259
[2]. Duchi J Hazan E and Singer Y 2011 Adaptive subgradient methods for online learning and stochastic optimization Journal of machine learning research 12(7)
[3]. Zeiler M D 2012 Adadelta: an adaptive learning rate method arXiv preprint arXiv 1212 5701
[4]. LeCun Y Bottou L Bengio Y and Haffner P 1998 Gradient-based learning applied to document recognition Proceedings of the IEEE 86(11) 2278-2324
[5]. He K Zhang X Ren S and Sun J 2016 Deep residual learning for image recognition In Proceedings of the IEEE conference on computer vision and pattern recognition pp 770-778
[6]. Krizhevsky A and Hinton G 2009 Learning multiple layers of features from tiny images
[7]. Woodworth B Patel K K Stich S Dai Z Bullins B Mcmahan B & Srebro N 2020 Is local SGD better than minibatch SGD? In International Conference on Machine Learning (pp. 10334-10343). PMLR
[8]. Lydia A and Francis S 2019 Adagrad—an optimizer for stochastic gradient descent. Int. J. Inf. Comput Sci 6(5) 566-568
[9]. Zeiler M D 2012 Adadelta: an adaptive learning rate method arXiv preprint arXiv:1212.5701
[10]. Zhang X Y Sun W Y and Chen Y 2023 Tackling the Non-IID Issue in Heterogeneous Federated Learning by Gradient Harmonization arXiv:2309.06692
Cite this article
Hu,M. (2024). AdaGCR: An improved method for optimizing machine learning training process. Applied and Computational Engineering,50,1-7.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 4th International Conference on Signal Processing and Machine Learning
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Bishop C M 2006 Pattern recognition and machine learning Springer New York p 259
[2]. Duchi J Hazan E and Singer Y 2011 Adaptive subgradient methods for online learning and stochastic optimization Journal of machine learning research 12(7)
[3]. Zeiler M D 2012 Adadelta: an adaptive learning rate method arXiv preprint arXiv 1212 5701
[4]. LeCun Y Bottou L Bengio Y and Haffner P 1998 Gradient-based learning applied to document recognition Proceedings of the IEEE 86(11) 2278-2324
[5]. He K Zhang X Ren S and Sun J 2016 Deep residual learning for image recognition In Proceedings of the IEEE conference on computer vision and pattern recognition pp 770-778
[6]. Krizhevsky A and Hinton G 2009 Learning multiple layers of features from tiny images
[7]. Woodworth B Patel K K Stich S Dai Z Bullins B Mcmahan B & Srebro N 2020 Is local SGD better than minibatch SGD? In International Conference on Machine Learning (pp. 10334-10343). PMLR
[8]. Lydia A and Francis S 2019 Adagrad—an optimizer for stochastic gradient descent. Int. J. Inf. Comput Sci 6(5) 566-568
[9]. Zeiler M D 2012 Adadelta: an adaptive learning rate method arXiv preprint arXiv:1212.5701
[10]. Zhang X Y Sun W Y and Chen Y 2023 Tackling the Non-IID Issue in Heterogeneous Federated Learning by Gradient Harmonization arXiv:2309.06692