1. Introduction

The origins of queuing theory can be traced back to analyses and studies related to the incoming call systems of telephone exchanges. Today, the application of queuing theory spans a diverse array of sectors, from telecommunications, computing, and transportation to logistics, warehouse management, and the layout of hospitals and factories. Urban planners harness queuing theory to refine public transportation systems—streamlining bus and train schedules, reducing wait times, and enhancing passenger throughput.

While there's no shortage of literature dedicated to the practical applications of queuing theory, there's a noticeable gap in research that critically analyzes, evaluates, and addresses the challenges in these applications. This paper seeks to delve into the intricacies and challenges that arise when queuing theory intersects with real-world scenarios, and when it's combined with other theoretical frameworks. By providing such an analysis, the intention is to offer clarity and guidance for scholars venturing into similar realms of research. Drawing from real-world use cases of queuing theory, this paper amalgamates findings from prior studies, offering fresh perspectives and novel insights.

2. Theoretical Foundations

2.1. Definition and Historical Evolution of Queuing Theory

A.K. Erlang's seminal 1909 paper, "Probability and the Telephone," is widely regarded as the inaugural publication in the realm of queuing theory [1]. This discipline, a specialized subset of operations research, delves deep into the intricacies of analyzing and modeling queues, aiming to enhance and fine-tune system performance. At its core, queuing theory seeks to pinpoint the ideal system configuration, encompassing factors like server count, system capacity, and the orchestration of arrivals and departures. Such a configuration would ideally curtail wait times, amplify throughput, and elevate overall efficacy.

Several pivotal concepts underpin queuing theory:

Arrival Rate: The frequency of work items entering the system.

Serving Rate: The speed at which tasks are processed by the server.

Queue Discipline: A guideline dictating the sequence in which tasks are addressed from the queue.

System Capacity: The ceiling on the number of tasks the system can accommodate.

Utilization: The proportion of time the server dedicates to task processing.

Little's Law: An elemental equation elucidating the relationship between average wait duration, the count of tasks within the system, and server utilization.

Queuing Model: An abstract, mathematical depiction of a queuing system's dynamics, examples being the M/D/1 and G/G/1 models.

By meticulously dissecting these principles and harnessing mathematical simulations to mirror queuing system behaviors, queuing theory furnishes invaluable perspectives. These insights aid in crafting systems that adeptly cater to client requirements, concurrently slashing lags and bolstering output.

2.2. Other Theories Discussed in This Study

Quality of Experience (QoE) represents the comprehensive assessment of customer satisfaction and interaction with a service or product, along with its respective provider, such as a webpage or television broadcast [2].

3. System Analysis and Empirical Research

3.1. Application of Queuing Theory in Network Communications

3.1.1. The Necessity for Queuing Theory in Contemporary Network Communications. Queuing theory plays a vital role in network communication performance as it provides a mathematical framework for analyzing and modeling the behavior of packets in communication networks. This allows network designers to optimize the network structure, reduce error rates [3], and improve resource utilization [4]. For example, network designers can use flow modeling to represent flow patterns in a network, which helps understand the dynamics of packet arrival and departure. This information is critical for designing efficient protocols and algorithms that can handle traffic efficiently.

3.1.2. Case Studies and Analysis: Queuing Theory in Network Communications

3.1.2.1. Use Queuing Theory to Calculate Appropriate Server Performance to Cope with Network Delays. In the process of network users obtaining services, users are always concerned about the waiting time of services, such as the loading of web pages and videos. For some services, even a pause event of just a few seconds can significantly degrade user-perceived quality of experience (QoE) [5]. Therefore, network designers need to reduce the possible waiting time for users. The process of the server processing requests issued by users can be modeled using queuing theory.

\( {π_{i}}={π_{0}}{ρ^{i}} \)

\( {π_{i}}=(1-ρ){ρ^{i}} \)

\( ρ=\frac{λ}{μ} \)

\( E[N]=\sum _{i=1}^{∞}(i-1){π_{i}}=(1-ρ)ρ\sum _{i=1}^{∞}(i-1){ρ^{i-1}}=(1-ρ)ρ(\sum _{i=1}^{∞}i{ρ^{i-1}}-\sum _{i=1}^{∞}{ρ^{i-1}})=(1-ρ)ρ(\frac{1}{{(1-ρ)^{2}}}-\frac{1}{1-ρ})=\frac{{ρ^{2}}}{1-ρ} \) (1)

The waiting time of a job in the queue can be obtained by Little's law (Formula 3)

\( E[{T_{q}}]=\frac{E[N]}{λ}=\frac{{ρ^{2}}}{(1-ρ)λ}=\frac{ρ}{1-ρ}∙\frac{1}{μ} \) (2)

The average waiting time in Figure 2 is about 9 times that of Figure 1. This means that the average wait time for users in Figure 2 is ten times longer than that of users in Figure.

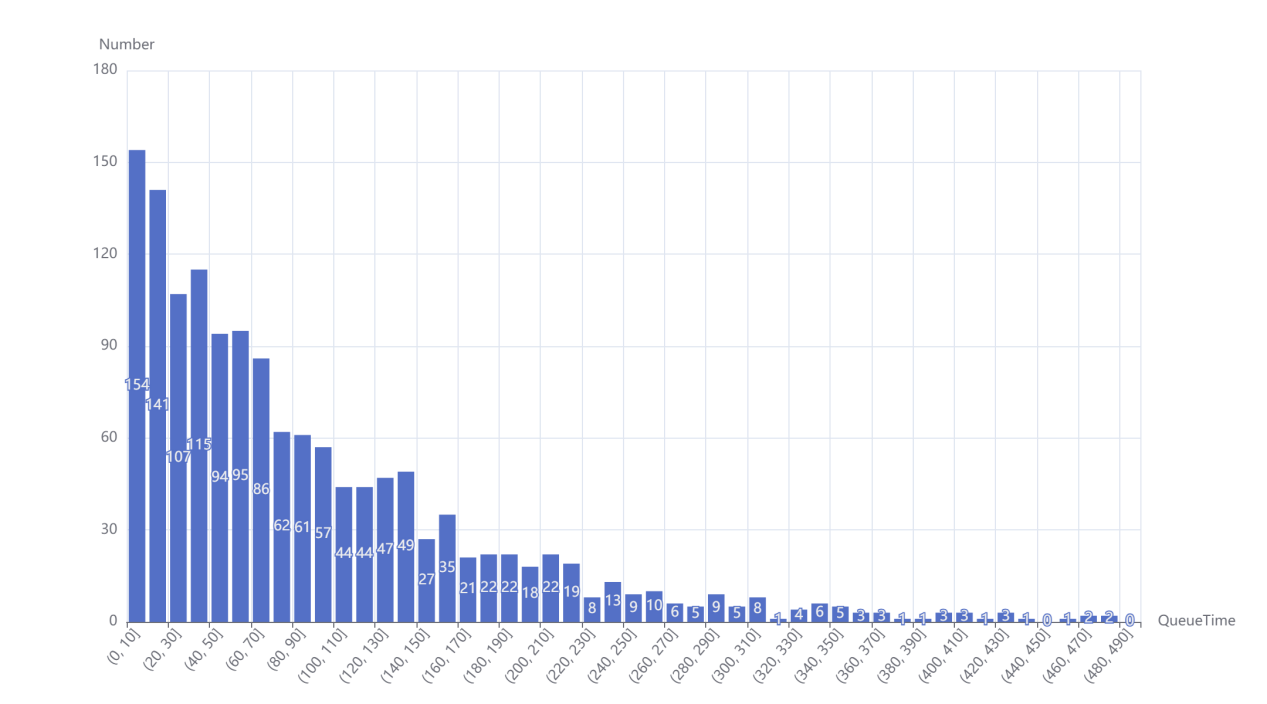
Figure 1. Statistics on waiting time, 3000 jobs are simulated, equipment utilization \( ρ \) = \( \frac{1}{2} \) (Photo/Picture credit: Original).

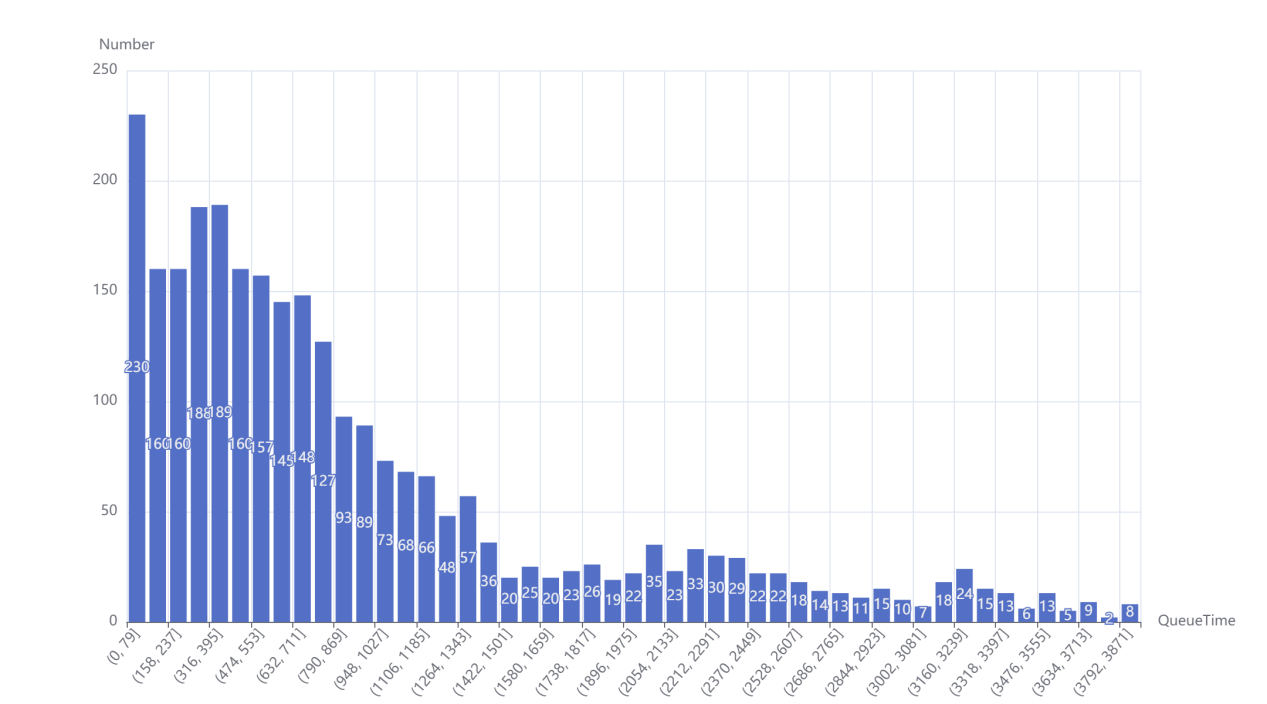
Figure 2. Statistics on waiting time, 3000 jobs are simulated, equipment utilization \( ρ \) = \( \frac{9}{10} \) , the average service rate μ of the server is the same as Figure 1 (Photo/Picture credit: Original).

When user requests to the network are close to the server's service capabilities, it means that users need to wait longer for their requests, which will greatly affect the user's mood. At the same time, in reality, the storage space of the server is limited. If there are too many jobs in the queue, data will overflow and cause failure [6]. Network designers need to reasonably plan server performance or add new servers based on user response to waiting time and the number of network requests to ensure that the network can run smoothly and stably.

3.1.2.2. Using Queuing Theory to Solve the Problem of Resource Quantity Calculation for Resource Scheduling in 6TiSCH Network. In 2013, the IETF initiated the 6TiSCH standards working group with the intent of integrating IPv6 into the realm of low-power, short-range wireless technology. This initiative aimed to address challenges associated with IP access for industrial field nodes and ensuring the reliability and predictability of communications within resource-constrained environments. The efficacy of the 6TiSCH network is significantly influenced by its scheduling methods. Consequently, academic circles have introduced autonomous resource scheduling algorithms, notably Orchestra and ALICE. The subsequent section will delve into a resource quantity computation solution, termed MY_SF, tailored for resource scheduling within the 6TiSCH network. This solution, rooted in queuing theory, was pioneered by the China University of Posts and Telecommunications [7]. Considering the volume of data packets and spatial dimensions, reference can be made to both formula 4 and formula 5.

\( {α_{n}}\begin{cases} \begin{array}{c} α , n=0, 1, 2, ..., {L_{q-1}} \\ 0 , n≥{L_{q}} \end{array} \end{cases} \)

\( {β_{n}}\begin{cases} \begin{array}{c} nβ , 0≤n \lt {N_{tx}} \\ {N_{tx}}β , {N_{tx}}≤n≤{L_{q}} \end{array} \end{cases} \) (3)

Similarly, the entry and exit of data packets have Markov properties, so formula 6 can be obtained.

\( \begin{cases} \begin{array}{c} {α_{0}}{p_{0}} ={β_{1}}{p_{1}} , n=0 \\ {(α_{n}}{+{β_{n}})P_{n}} ={α_{n-1}}{P_{n-1}} +{β_{n+1}}{P_{n+1}}, n \gt 0 \end{array} \end{cases} \) (4)

According to Equations 4, 5, and 6, the probability of state n (Formula 7) and the probability of state n when the amount of data inputs and outputs reaches a balanced state (Formula 8) can be obtained.

\( {p_{n}}=\frac{{{α_{n-1}}{α_{n-2}}...α_{0}}}{{{β_{n}}{β_{n-1}}...β_{1}}}{p_{0}} \)

\( {p_{n}}=\begin{cases} \begin{array}{c} \frac{{ρ^{n}}}{n}{p_{0}} , 0≤n \lt {N_{tx}} \\ \frac{{ρ^{n}}}{{N_{tx}}N_{tx}^{n-{N_{tα}}}}{p_{0}} , {N_{tx}}≤n≤{L_{q}} \end{array} \end{cases} \) (5)

According to formulas 4, 5, 7, and 8, the probability that there is without any data packet in the buffer queue \( {p_{0}} \) can be obtained (formula 9).

\( {p_{0}}={(\sum _{n=0}^{{N_{tx}}-1}\frac{{ρ^{n}}}{n!}+\frac{{ρ^{{N_{ax}}}}(1-{(\frac{ρ}{{N_{tx}}})^{{L_{q}}-{N_{ax}}+1}})}{{N_{tx}}!(1-\frac{ρ}{{N_{tx}}})})^{-1}} \) (6)

The average cache queue length E ( \( {L_{avg }} \) ) can be also derived from Formula 8 (Formula 10).

\( E({L_{avg }})=\sum _{n={N_{ax}}}^{{L_{q}}}(n-{N_{tx}}){p_{n}} =\sum _{n={N_{ax}}}^{{L_{q}}}n{p_{n}}-{N_{tx}}\sum _{n={N_{tx}}}^{{L_{q}}}{p_{n}} =\sum _{n=0}^{{L_{q}}}n{p_{n}}-\sum _{n=0}^{{N_{ax}}-1}{np_{n}}-{N_{tx}}(1-\sum _{n=0}^{{N_{ax}}-1}{p_{n}}) =E({L_{q}}+{N_{tx}})-\sum _{n=0}^{{N_{ax}}-1}{(n-{N_{tx}})p_{n}}-{N_{tx}} \)

(7)

The average amount of packets E( \( {L_{avg }} \) + \( {L_{q}} \) ) in a node is as follows (Formula 11):

\( E({L_{avg }}+{N_{tx}})=E({L_{avg }})+{N_{tx}}+{p_{0}}\sum _{n=0}^{{N_{ox}}-1}\frac{(n-{N_{tx}}){ρ^{n}}}{n} \) (8)

The average amount of occupied units \( \bar{s} \) is as follows (Formula 12):

\( \bar{s}=E({L_{avg }}+{N_{tx}})-E({L_{avg }}) \)

\( {λ_{e}}=λ(1-{p_{k}}) \)

\( {W_{s}}=\frac{E({L_{avg }}+{N_{tx}})}{{λ_{e}}} \)

\( {W_{q}}=\frac{E({L_{avg }})}{{λ_{e}}}={W_{s}}-\frac{1}{β} \) (9)

Through the above formula, network designers can predict many attributes of the system. This attributes can guide network designers to better design network. By modeling queues and analyzing their behavior, network administrators can guarantee a certain level of quality of service for various applications. Simultaneously, queuing theory can be used to determine whether new calls should be accepted into the network. By analyzing the current state of the network and the expected load on the network, queuing models can help network administrators make decisions about call acceptance control to ensure that the network does not become overloaded and provide poor service to existing calls. However, network administrators must also pay attention to the actual situation when applying queuing theory. Network administrators must apply queuing theory correctly based on specific needs.

3.2. Application of Queuing Theory in Public Place Planning

The Imperative of Queuing Theory in Urban Planning. Queuing theory stands as a crucial instrument in urban planning, adept at streamlining and optimizing pedestrian flow across various public domains such as transport hubs, retail centers, medical facilities, and amusement parks. This mathematical approach empowers urban designers to capitalize on spatial efficiency, guiding them toward optimal designs that not only host maximal foot traffic but also circumvent potential overcrowding or lag. Furthermore, queuing theory plays a pivotal role in curtailing wait times by spotlighting congestion points and fine-tuning the operational capacity of structures such as ticket booths, security checks, and attraction lines. Real-world Insights: The Role of Queuing Theory in Urban Spaces. An imperative for railway station architects and administrators is the judicious design of ticket booths to avert undue delays for patrons. Consequently, a nuanced model becomes indispensable for a holistic grasp of the dynamics at play during the conceptualization and governance of such ticket counters. Research conducted at the NSG-3 railway stations over a seven-day span [8] facilitated data accumulation, which upon analysis, aligned seamlessly with a single-server queuing paradigm. This indicates that railway design teams and overseers could potentially harness the M/G/1 model as a planning foundation. Nonetheless, the scope of this study was confined to a select few regions in Southern India, necessitating a more expansive on-site evaluation before embracing this model universally. Harmonizing Queuing Theory with Complementary Schemas in Urban Design. Strategies for Incorporating Queuing Theory into Urban Spaces. Prior to deploying any design solution, urban planners should possess a comprehensive understanding of the specific ecosystem they're dealing with. This entails a thorough examination of factors like patron influx rates, service intervals, and overall capacity to pinpoint the primary contributors to gridlocks and lags [9]. Distinct regions, and even varying timeframes within them, will exhibit disparate patterns of arrivals and service distributions. This necessitates a tailored approach where designers actively engage in field assessments to ascertain the most apt model and the associated parameters for their unique situation [10].

4. Conclusion

This article introduces a series of modeling optimization strategies rooted in queuing theory tailored to specific real-world scenarios. While designers can select models that seem to best match their current conditions, it's imperative to recognize that disparities often exist between theoretical models and the intricacies of real-life situations. Thus, it falls upon the designer to refine these models, ensuring they are more congruent with the multifaceted realities they encounter. Additionally, owing to the constraints in the scope of this article, the exploration into the specific applications of queuing theory might not sufficiently address the myriad challenges present in everyday production and living conditions. Such constraints shouldn't be viewed as limitations but rather as starting points. There exists a vast expanse of opportunities for future researchers and scholars to delve deeper into this domain. By further investigating and encapsulating the myriad directions and nuances of queuing theory, they can bring forth more comprehensive solutions and insights that can bridge the gap between theoretical ideals and the ever-evolving dynamics of real-world scenarios.