1. Introduction

Recommender systems have become a cornerstone of the digital landscape, guiding users to products, media, and connections tailored to their preferences. These systems are often powered by Multi-Armed Bandit algorithms, which strike a balance between exploring new items and exploiting known preferences. However, the effect of biased initialization on these algorithms is not well understood, despite its potential to skew recommendations and degrade user experience. This study is structured into three segments. The first examines the definition of four prevalent MAB algorithms: Epsilon Greedy, Explore Then Commit, Upper Confidence Bound, and Thompson Sampling within recommender systems. The second assesses how biased initialization could impact the performance of these algorithms. The third outlines the experimental design aimed at evaluating the algorithms' responses to biased starts within a simulated recommender system environment governed by a binomial distribution. A quantitative approach will be utilized to conduct this experiment, enabling a direct comparison of the MAB algorithms' adaptability and the quality of their recommendations under biased initial conditions. The generated data will reveal each algorithm's resilience and capability to recover and provide high-quality recommendations over time. The significance of this research is two-fold. It offers insights into enhancing recommender systems' robustness, potentially improving user satisfaction in various digital service industries. Furthermore, it addresses a gap in the empirical understanding of MAB algorithms' performance under biased initialization, thereby enriching the theoretical discourse in the domain of adaptive recommendation algorithms.

2. Multi-armed Bandit

2.1. Summary of the Bandit Problem

The multi-armed bandit problem encapsulates a fundamental challenge in decision-making under uncertainty, requiring a balance between exploiting known rewards and exploring unknown possibilities. This dilemma is analogized to a gambler facing several slot machines, each with its own set of rewards distributed according to unknown probabilities. The gambler must choose which machine to play (or arm to pull), with the goal of maximizing their total payoff over time. This pursuit is complicated by the fact that each choice not only offers the chance for immediate reward but also serves as a learning opportunity that could inform better decisions in the future. The concept of 'regret' in this context is the difference between the rewards obtained and the rewards that would have been obtained by always choosing the best arm. Strategies, or 'policies,' for MAB problems, aim to navigate this exploration versus exploitation trade-off efficiently, leveraging historical data to inform future pulls while mitigating the potential for missed opportunities and unnecessary losses. [1].

In the realm of recommender systems, the application of Multi-Armed Bandit algorithms represents a departure from classical collaborative filtering techniques, standing out for their dynamic, performance-oriented decision-making process. At the core, MAB algorithms tackle the exploration-exploitation dilemma—whether to recommend items with known high user preference (exploitation) or to suggest new items whose performance is uncertain (exploration). This section will explore the nuances and current applications of four quintessential MAB algorithms: Epsilon Greedy, Explore Then Commit, Upper Confidence Bound (UCB1), and Thompson Sampling [2].

2.2. MAB Algorithms

Epsilon Greedy is the simplest of the MAB algorithms, renowned for its straightforward approach that allows for a predetermined proportion of exploration. It operates by typically suggesting the best-known option, but with a small probability (epsilon), it will randomly recommend an alternative to the user. This algorithm’s simplicity is also its drawback, as it does not adjust its exploration rate over time, which can be inefficient in adapting to a user’s evolving preferences. [3]

The Explore Then Commit algorithm segments the decision-making process into two distinct phases. Initially, it dedicates a set period for exploration, gathering data on user preferences. Once this phase concludes, it commits to the best-performing option. The challenge with ETC is determining the optimal duration of the exploration phase—a misestimation can either lead to premature commitment or excessive exploration [4].

Upper Confidence Bound, on the other hand, introduces a more sophisticated balance between exploration and exploitation by incorporating uncertainty in its decision-making. It calculates a confidence interval for the estimated value of each option and preferentially selects options with higher upper confidence bounds. This allows UCB1 to naturally decrease exploration over time as it becomes more certain about user preferences, making it more adaptable to user behavior than Epsilon Greedy or ETC [5].

Thompson Sampling, often hailed for its efficiency, utilizes a probabilistic approach. It models the problem using Bayesian inference, creating a distribution of probabilities for the likelihood that each option is optimal. Selections are made based on random draws from these distributions, inherently balancing exploration and exploitation by considering both the success rate and the uncertainty of each option. Its strength lies in its ability to continuously update these distributions with new data, providing a highly responsive and personalized user experience [6].

Each of these MAB algorithms is actively employed in various recommender systems, reflecting a commitment to enhance user satisfaction through more personalized content delivery. As they are embedded into the framework of platforms ranging from e-commerce to content streaming, the necessity for a deeper understanding of their operational efficacy, particularly under challenging conditions like biased initialization, becomes ever more pressing. This exploration underscores the importance of the subsequent analysis, which will critically examine how each algorithm stands up to the initial bias and whether they maintain their recommendation integrity when faced with skewed starting data.

3. Biased Initialization

3.1. Definition of a biased initialization

Biased initialization in the context of Multi-Armed Bandit algorithms refers to the scenario where the initial conditions for decision-making—such as early rewards or user preferences—are pre-set or inferred in a way that does not accurately reflect the true state of the environment. This misrepresentation can stem from a variety of sources, including historical data that is not representative of the current user base, previous interactions that favor certain choices, or even the deliberate priming of the system to test specific hypotheses. In essence, biased initialization is akin to beginning a race with some runners unfairly positioned ahead of others; it distorts the starting line and can significantly influence the course and outcome of the race.

3.2. Impact of Biased Initialization

The potential impacts of biased initialization on the efficacy of MAB algorithms are multi-faceted and profound. MAB algorithms are designed to learn and adapt over time based on the feedback received from their environment—in this case, user interactions. When the initial conditions are biased, it can skew the algorithm's learning process. For instance, an algorithm might be misled into believing that a particular choice is more favorable than it actually is, resulting in an overemphasis on exploitation of that choice at the expense of exploring others. This premature commitment can lead to a feedback loop where only a subset of options are continuously presented to the user, further reinforcing the initial bias.

Moreover, biased initialization can hinder the algorithm’s ability to accurately estimate the value of each action. MAB algorithms rely on these estimates to make balanced decisions between exploring new options and exploiting known ones. When the initial estimates are skewed, the algorithm’s exploration strategy can become overly conservative or excessively risky, neither of which is conducive to optimal performance. In conservative scenarios, the algorithm may miss out on discovering potentially superior options. Conversely, in risky scenarios, it might persist in exploring suboptimal choices, degrading the user experience and reducing overall system effectiveness.

In general, the consequence of biased initialization is the distortion of the MAB algorithm's innate ability to adaptively optimize its strategy. It undermines the principle of learning from a neutral, unbiased standpoint, potentially causing long-term detriments to the quality of the recommendation. Given the critical role that accurate and personalized recommendations play in user engagement and satisfaction, understanding and mitigating the effects of biased initialization is of paramount importance. This understanding will enable the development of more robust MAB strategies that can deliver reliable and fair recommendations, even when faced with imperfect starting conditions.

4. Experiment

4.1. Simulated Environment Setup

Building upon the insights into the potential ramifications of biased initialization on MAB algorithms, the experimental design aims to systematically evaluate the robustness of the aforementioned algorithms: Epsilon Greedy, ETC, UCB1, and Thompson Sampling. The experimental procedure is underpinned by a simulated recommender system environment, where the items' reward probabilities adhere to a binomial distribution, emulating the probabilistic nature of user preferences in real-world scenarios.

A simulation experiment is conducted to compare the performance of four different multi-armed bandit algorithms: Epsilon Greedy, Explore Then Commit, Upper Confidence Bound, and Thompson Sampling. These algorithms are used to make decisions in a scenario where there are two options (or "arms") to choose from, each with different probabilities of providing a reward. The goal is to minimize regret over a series of trials.

The two arms have "true" probabilities of yielding a reward, with arm 0 having a slightly higher chance (55%) compared to arm 1 (45%). To introduce a level of complexity, the algorithm is initially provided with "reversed" probabilities, intended to bias its early decisions.

The experiment consists of 10,000 trials and is repeated 10 times to gather average performance metrics. For the first 1,000 trials, the reversed probabilities are used to simulate the bandit pull, after which the true probabilities are applied. Regret is calculated at each trial as the difference between the optimal rewards that could have been obtained had the best arm been chosen every time, and the actual rewards obtained following the choices made by the algorithms.

Each algorithm has its own strategy for arm selection. Epsilon Greedy occasionally explores randomly, but mostly exploits the arm with the highest estimated value based on past rewards. Explore Then Commit explores randomly for the first 3,000 trials and then commits to the arm with the highest estimated value thereafter. UCB1 balances exploration and exploitation by considering both the estimated value of the arms and the uncertainty about that estimate. Thompson Sampling uses a Bayesian approach, where it samples from a probability distribution (a Beta distribution in this case) to determine the arm to select, with the distribution parameters updated based on observed rewards.

The results of the experiments are captured in two ways: cumulative regret over time for each algorithm and the count of selections for each arm across all experiments. Cumulative regret is plotted to show how quickly and effectively each algorithm learns to make better decisions over time.

4.2. Result

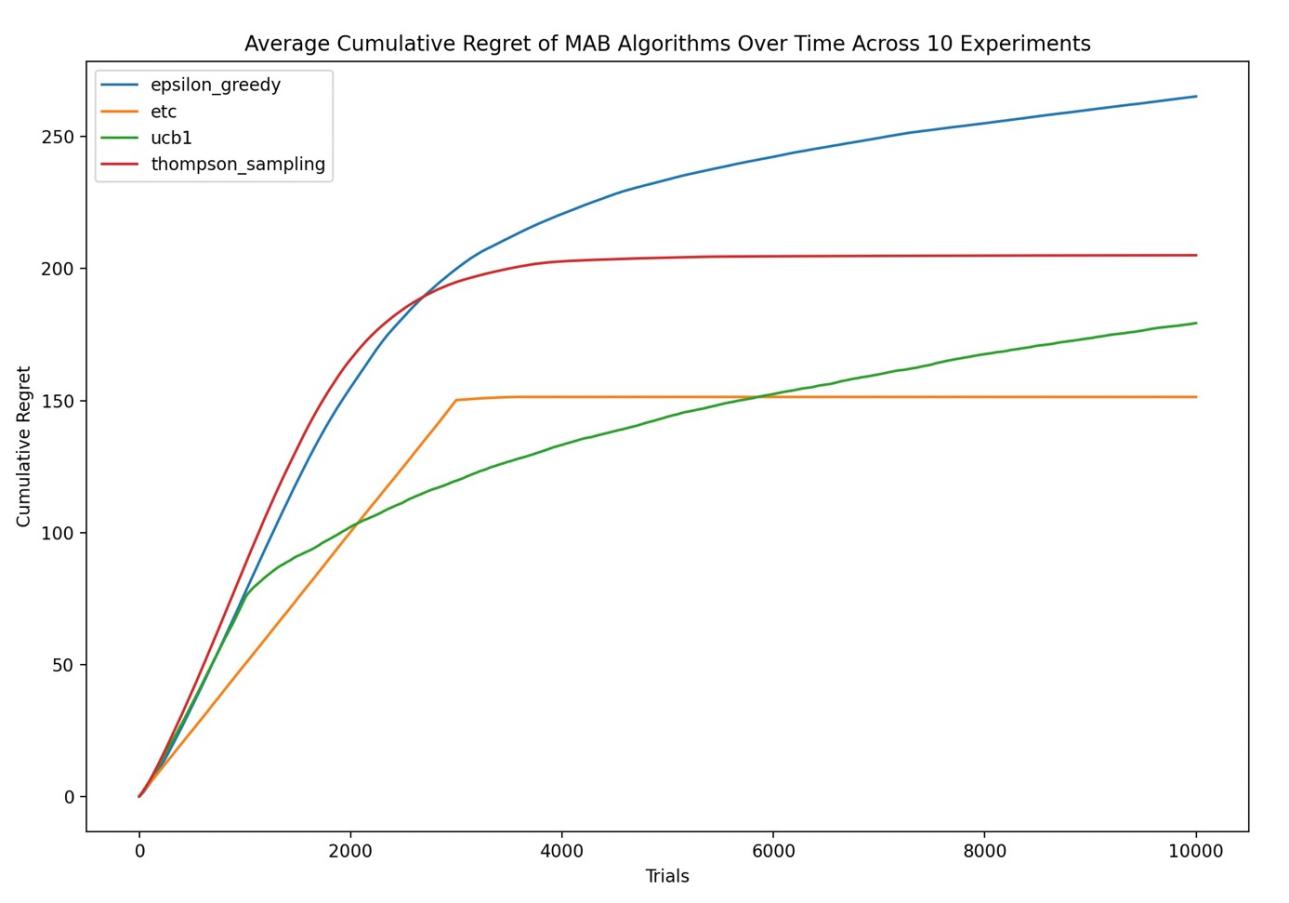
Figure 1. Average Cumulative Regret of MAB Algorithm Over Time Across 10 Experiments

As shown in Figure 1, epsilon-greedy appears to have the highest cumulative regret among the four, indicating that it may not have performed as well as the others in this experiment. However, the curve's slope becomes flatter as trials increase, suggesting that the algorithm's performance improves over time. The epsilon-greedy algorithm balances exploration and exploitation by selecting random actions with probability epsilon and the best-known action with probability 1 minus epsilon.

The performance of the ETC algorithm shows an initial steep rise in regret, then plateaus sharply and remains constant. This reflects the algorithm's nature: it explores each arm for a predetermined number of times and then commits to the arm that performed best during the exploration phase. The plateau indicates that after a certain number of trials, no further regret is accumulated, suggesting that it has found the best arm and continues to exploit it. However, if the initial exploration does not identify the optimal arm (possibly due to biased initialization), the regret will not improve over time, as indicated by the flat line.

UCB1 shows a steadily increasing curve of cumulative regret, though it's significantly lower than that of the epsilon-greedy algorithm. The UCB1 algorithm is designed to balance exploration and exploitation by considering both the average reward of the arms and the uncertainty or variance associated with each arm. The increasing curve suggests that while it may be affected by the bias, it continues to explore and exploit in a balanced manner over time.

Thompson Sampling's curve, while not the lowest in cumulative regret, shows a steady increase, suggesting a consistent approach to balancing exploration and exploitation over time. The cumulative regret is higher than that of the ETC after its plateau, but lower than the epsilon-greedy algorithm. Thompson Sampling chooses actions based on the probability of each action being optimal, given the observed rewards so far. This Bayesian approach should allow the algorithm to adjust its estimates as it gathers more data, even if the initial estimates are biased. Despite not having the lowest regret, its performance indicates that it is effectively updating its beliefs about the arms and finding a balance between trying out different arms and exploiting the ones that have given the highest rewards so far. Its relatively low and steady increase in regret implies that it is quite robust to initial biases, as it does not stick to potentially suboptimal choices made due to biased initialization but rather continues to refine its understanding of each arm's reward probability.

5. Conclusion

This research provides a comprehensive examination of how biased initialization affects the performance of various Multi-Armed Bandit (MAB) algorithms—Epsilon Greedy, Explore Then Commit (ETC), Upper Confidence Bound (UCB1), and Thompson Sampling—within the context of a simulated recommender system environment. Our findings highlight significant differences in how each algorithm copes with and adjusts to the presence of initial bias over 10,000 trials. Epsilon Greedy exhibited the highest cumulative regret, indicating a less efficient approach in this scenario. ETC showed a rapid accumulation of regret that plateaued, reflecting its deterministic exploration period followed by unwavering exploitation. UCB1's performance, though better than Epsilon Greedy, still revealed a consistent increment in regret, suggesting some susceptibility to initial bias but a more balanced long-term approach. Thompson Sampling, despite not achieving the lowest cumulative regret, demonstrated a robustness to bias with a steady increment in regret, showcasing its adaptive nature and ability to recover from a biased start.

One significant limitation of this study is the rigid structure assigned to the ETC algorithm. In real-world applications, the duration of the exploration phase is not pre-determined, as it was in this experimental setup. This is a critical factor as the ETC's efficacy greatly depends on how well the exploration phase is executed before commitment.. Future research could focus on dynamic exploration periods for ETC that adjust in response to the observed outcomes, potentially improving its adaptability to biases.

Another limitation is the assumption of a binomial reward distribution. In reality, user preferences and item rewards are governed by more complex distributions and influenced by a myriad of factors not accounted for in a binary setting. Future studies could incorporate more intricate distributions and user models to simulate a more realistic and varied environment.

In conclusion, this study serves as a foundational step towards understanding the implications of biased initialization in MAB algorithms and sets the stage for future explorations in this field. It calls attention to the necessity for robust algorithms that can maintain the integrity of recommendations despite imperfect conditions and underscores the importance of ongoing algorithmic refinement to enhance user satisfaction in digital service platforms.