1.Introduction

Knowledge graphs(KGs), which are structured information carriers, have broad application prospects in the fields of knowledge management, intelligent applications, and data analysis. KGs can be classified into two categories: general domain KGs and specific-domain knowledge graphs, depending on the fields they cover. Typical examples of general KGs are Freebase [1], WordNet [2], Yago[3], etc, which are mainly used to describe commonsense knowledge and universal laws. A large number of high-quality domain-specific KGs have been released in recent years [4][5][6]. Due to the different scope of knowledge covered, the characteristics of knowledge inside the graph are very different. In general, the knowledge structure of the domain-specific KG is more complex, and the relationships between entities are more diverse. In contrast, the knowledge structure of the commonsense KG tends to be flat and loose-structured.

The ability of KG to make interpretable reasoning on structured information is an important support for many research tasks^. Knowledge graph reasoning refers to the process of reasoning about new triples by using the existing triples in the KGs. In this process, adding rule constraints can effectively improve the accuracy and reliability of reasoning. Rule-based KG reasoning methods excel at performing inference by uncovering underlying logical rules, showcasing remarkable generalization ability and interpretability. Moreover, the flexibility of logical rules allows for seamless integration with diverse neural network models, thereby offering promising prospects for research and application.

Although rule constraints can be used as a strong support for KG reasoning, the acquisition of rules and the quality of rules are crucial for reasoning under rule constraints. For a long time, it is difficult to obtain rules with high quality and reliability on a large scale, and to improve reasoning performance due to the lack of accuracy of rules obtained by automatic or semi-automatic means. A serious problem is that there are usually no extensive data sources for a specific domain and the data size is usually small, which makes automatic extraction of rules very difficult. To solve the above problems, this paper proposes a method for automatic rule extraction in a low-resource way for domain-specific KGs. This method automatically extracts rule instances through predefined rule patterns, and uses the generative adversarial networks(GANs) for training. Finally, more rule instances conforming to the rule pattern are generated, and the rules with high quality and high reliability are mined.

2.Related Work

2.1.Rules in Knowledge Graph

The practice of introducing rules into KGs has been concerned since the emergence of KGs, and there are various forms of introducing rules. At present, the rules that are applied to support reasoning in the field of KG are mainly divided into three categories: Logical Rules:represents the foundational approach to knowledge representation in KGs. First-order logic (FOL) [7] serves as the cornerstone for formalizing knowledge and inferring logical relationships. Horn rule logic [8], a subset of FOL, is particularly well-suited for KG representation due to its emphasis on declarativity and interpretability. Association Rule Mining :To address the inherent limitations of logic rules, researchers have developed association rule mining algorithms. AMIE [9] is designed to efficiently extract association rules from KGs.Subsequent works [10][11] have made technical adjustments in search pruning, search parallelization, search space optimization, etc. Even so, it is still difficult to cope with the increasing size of the graph. Probabilistic Soft Logic Rules: The representative work has Markov logic network (MLN) [12] establishes a probabilistic graphical model by leveraging predefined rules and factual information extracted from the KG.

Their applicability is constrained to precise reasoning, lacking the ability to represent uncertainty information and noisy data and cannot overcome the problems of rule-based reasoning, such as low tolerance to noise data, high cost of manual intervention, and difficulty in dealing with the growing scale of graphs.

2.2.Generative Adversarial Networks in Knowledge Graph

Generative models are indispensable techniques in unsupervised learning tasks. In recent years, their applications to KGs have become increasingly popular. A number of research efforts have incorporated the generative adversarial network (GAN) framework into KG manipulation. KBGAN [13] employs adversarial learning to generate high-quality negative training samples, which supersedes the conventional method of uniform sampling and leads to improved KG embedding (KG embedding). Another GAN-based framework, IGAN [14], addresses the need for effective negative sampling in KG completion by generating optimal negative samples. This provides non-zero loss scenarios for the discriminator, enabling it to leverage a margin-based ranking loss for maximum efficiency. KSGAN [15] builds on KBGAN by employing a selective adversarial network to generate even better training examples for negative cases.

While these methods leverage the adversarial element of GANs to achieve a level of refinement in the constraint accuracy of various rules during the reasoning process, their impact on the rule generation phase is less pronounced. Consequently, they do not directly contribute to the overall improvement of rule-based reasoning performance. This paper proposes a novel approach that directly integrates GAN with the rule generation stage. It aims to achieve a foundational enhancement in the quality of rule constraints, ultimately leading to a substantial improvement in the effectiveness of rule-based reasoning.

3.Model

3.1.Rule Pattern Modeling

The modeling of rules in this paper involves two levels: rule instances and rule patterns. A rule pattern is defined as the composition of multiple relations with structure according to the semantic logic relationship. A rule instance is a structured combination of multiple triples that conform to a rule pattern in the KG. For example, relation _husband_of, and relation _mother_of can semantically deduce relation _father_of, then the combination of above relations with the specific structure is treated as a regular pattern: (_husband_of&_mother_of\( ⟹ \)_father_of). Correspondingly, there may be multiple rule instances in the KG that conform to the rule pattern, such as: (Yao Ming, _husband_of, Ye Li) & (Ye Li, _mother_of, Yao Qin Lei)\( ⟹ \)(Yao Ming , _father_of, Yao Qin Lei ).

The basic idea of this paper for rule mining is to use a generative network to generate rule instances that conform to the rule pattern under the constraints of the rule pattern. Therefore, this paper models the regular patterns from three dimensions and incorporates this information into the training of the GAN model. In order to fully represent the structural information derived from the internal KG in the embedding space, we expect the vector representation of entities in the continuous space to exhibit the structure consistent with the feature subgraph. That is, the embedding vectors of entities in the embedding space have similar geometric characteristics as the subgraphs of the KG spectrum, and the geometric characteristics can be measured by the angle and distance in the continuous space. Therefore, we can use three sets of parallel terminology to describe the rule pattern: the feature subgraph structure of the KG, the logical expression of the relationship, and the structural information of the entity vector in the embedding space. And every rule pattern can be expressed precisely in the three parallel narrative ways respectively.

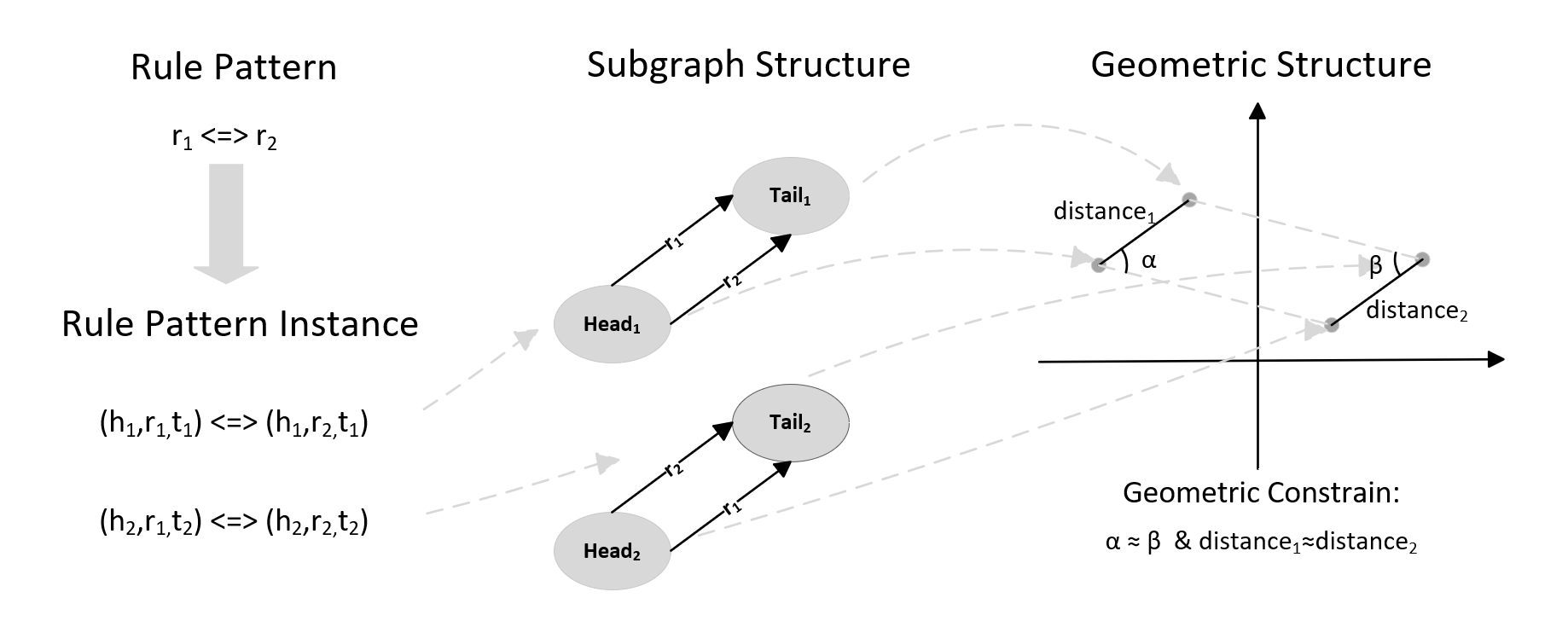
Figure 1. parallel dimensional modeling of regular patterns

Figure 1 takes the rule pattern of equivalence relation as an example, assuming that r₁ and r₂ are equivalent to each other, that is, they can maintain the same or similar semantics in the case of mutual replacement. According to the rule pattern that r₁ is equivalent to r₂, two rule instances conforming to the rule pattern are searched in the graph. The subgraph structure of each rule instance in the KG maintains a fixed structural feature, which is determined by the rule pattern. Since triples in a KG that conform to this rule pattern have a fixed subgraph structure, we expect these entities to retain this fixed structure when embedded in a continuous space, the structure can be accurately measured by distance and angle in a vector space. This measure provides the possibility to reshape the structure of embedding vectors in vector space according to the subgraph structure of KG.

3.2.GAN Taining Architecture

In the network architecture of GAN, we use two LineaRE [16] models as generators and discriminators, respectively. The complete training process of the GAN architecture is shown in figure 2.

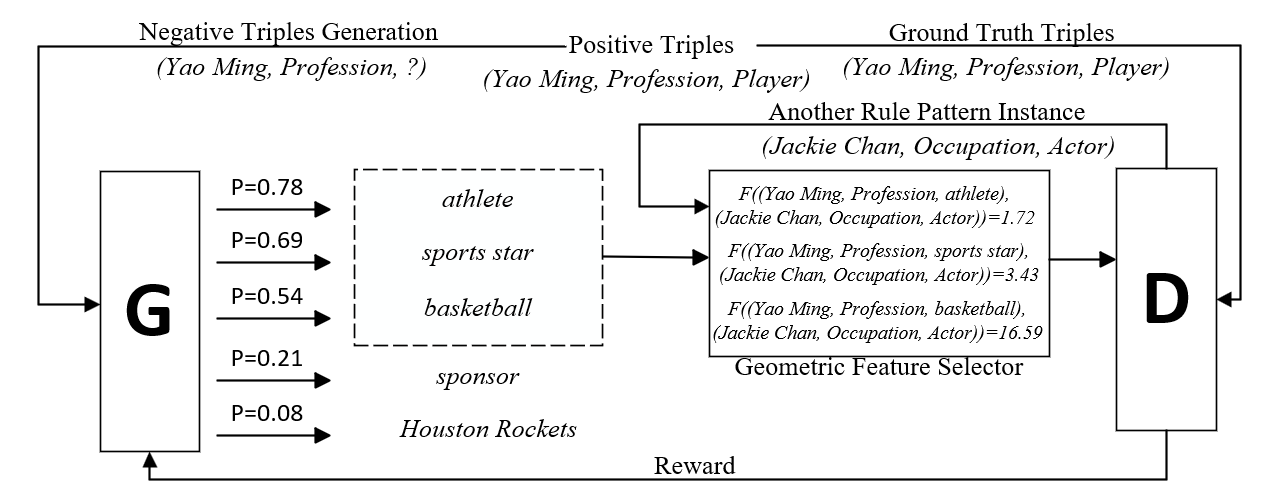
Figure 2. GAN training framework incorporating geometric information

Firstly, the training samples are selected from the rule set, taking the positive triple shown in the figure as an example: (Yao Ming, _Profession, Player). In the form of link prediction task, the head entities and relations are used as the input of the generator, and a set of outputs of the generator are obtained. The top three predicted tail entities in these outputs are selected, and the remaining negative triples are regarded as having obvious semantic errors and discarded. The process by which the generator gives the prediction of the tail entity adopts the LINeare model manner, as shown in Equation 1, where\( w_{r}^{1} \),\( w_{r}^{2} \), and\( {b_{r}} \)are the learnable parameter matrices and vectors of relation r as a linear map.

\( {f_{r}}(h)={w_{r}^{{2}^{-1}}} \circ (w_{r}^{1} \circ h+{b_{r}})=t\ \ \ (1) \)

On the other side of the top part of the figure, the positive triple goes through the rule matching process to search for different rule instances belonging to the same rule pattern, take the triple in the figure(Jackie Chan, _Occupation, Actor) as an example.

Following the rule modeling method mentioned above, different rule instances under the same rule pattern are expected to have the same geometric structure in the vector space, so the F function is used to calculate the geometric distance between the candidate negative triples and the triples obtained by rule matching, and the one with the smallest distance is selected and passed to the discriminator for adversarial training. The function F considers the distance and angle of the entity vector in the continuous space, so as to limit the convergence of the rule instance to the rule pattern it belongs to in the embedding space. The specific calculation formula of F function is shown in Formula (2-4):

\( F({T_{1}},{T_{2}})=λ|dis({T_{1}})-dis({T_{2}})|+(1-λ)|angle({T_{1}},{T_{2}})-angle({T_{2}},{T_{1}})|\ \ \ (2) \)

\( dis(T)={∥h-t∥_{2}}\ \ \ (3) \)

\( angle({T_{i}},{T_{j}})=\frac{{(h_{i}}-{t_{i}})∙{(t_{j}}-{t_{i}})}{{{∥h_{i}}-{t_{i}}∥_{2}}{{∥t_{j}}-{t_{i}}∥_{2}}}\ \ \ (4) \)

\( {∥∙∥_{2}} \)is used to measure the Euclidean distance in space of the embedding vectors of head and tail entities. T is a triple:\( T=(h,r,t) \). Finally, based on the received negative triples and the initial positive triples, the discriminator performs the marginal loss calculation and returns the feedback to the generator, which can be calculated by Eq. 5:

\( Loss=\sum _{(h,r,t∈Τ)}\sum _{({h^{ \prime }},r,{t^{ \prime }}∈{T^{ \prime }})}max⁡(0,score(h,r,t)-socre({h^{ \prime }},r,{t^{ \prime }})+γ)\ \ \ (5) \)

The scoring function is used to evaluate the confidence of the triples, that is, the likelihood of semantic accuracy. The scoring function still uses the original formula 6 of LIneaRE's model:

\( score(h,r,t)={score_{r}}(h,t)=∥w_{r}^{1}∘h+{b_{r}}-w_{r}^{2}∘t{∥_{1}}\ \ \ (6) \)

The loss calculated from the scoring function is returned to the generator as feedback, then generator adjusts its parameters based on reward, and the higher its performance, the more likely it is that the generated negative triples are semantically accurate.

4.Experiments

4.1.DataSets

In this paper, three datasets are used to verify the performance of the proposed method, which are WN18 dataset in the general domain, Bri-KGC dataset in the bridge management and maintenance domain, and Med-KGC dataset in the medical common knowledge domain. The statistics are shown in table 2.

Table 1. Detailed statistics of the three datasets used in the experiments

4.2.Evaluation Metrics

When testing the discriminator, this paper uses three common evaluation indicators of link prediction tasks: Mean Reciprocal Rank (MRR), Mean Rank (MR) and hit range (Hits@n, %) to measure the performance of the proposed method. When testing the generator, the evaluation metric used is accuracy. Accuracy refers to the ratio of correctly predicted triples to the total predicted triples, it usually is applied to evaluate the quality of classification models in triple classification task.

4.3.Baseline methods

Our models are compared with following baseline classical models used to solve link prediction tasks:

ComplEx[17] model solves the problem of KG link prediction based on the overall idea of latent factorization. QuatDE[18] model adopts dynamic mapping strategy to explicitly capture various relationship patterns of entities. ConvE[19] model uses convolutional neural networks to learn the representation of entities and relations, which treats the representation of entities and relations as pixels in an image, and then uses convolutional neural networks to learn the relationship between these pixels. KBGAN(TransD+ComplEx): taking pre-trained model TransD as discriminator and ComplEx as generator.

4.4.Results

Following KBGAN, our model also utilizes pre-training models (e.g.LineaRE) as generator and discriminator in the adversariallearning network. In pre-training process, the aforementioned models are trained 10000 epochs, taking 1024 training data as mini-batch. the dimension of embedding vectors is set to 512 and the scoring function uses L2 distance. It can be seen from table 2 that the proposed method has comparable performance with other models in Hit@10, MR And MRR indicators, it shows that our model can effectively search entities with low confidence but conforming to rules, which is of great help for mining high-quality rules to constrain downstream tasks.

Table 2. Results compared to baseline model performance

5.Conclusion

Aiming at the problems of low rule quality and insufficient structural knowledge mining depth in KG rule mining tasks, this paper proposes a KG rule mining method of joint rule pattern under the adversarial generative network architecture. This method models rule patterns by introducing geometric properties, and then mines rule instances under the guidance of rule patterns. The experimental results show that the proposed method can improve the performance of the KG completion task in the bridge management and maintenance field and the medical common sense field, and can also adapt to the KG completion task in the public domain.