1. Introduction

Brain Magnetic Resonance Imaging (MRI) is a cornerstone in contemporary diagnostic practices, providing non-invasive insights into both anatomical structures and functional dynamics [1]. Despite its effectiveness, the fidelity of MRI images is susceptible to motion artifacts, especially pronounced during brain imaging. Even subtle translational shifts resulting from patient movements can introduce distortions, compromising the precision and accuracy of scans and potentially posing diagnostic challenges. Understanding the nature of head motion in brain MRI is crucial; it can be categorized as rigid (involving translation and rotation) or non-rigid/deformable [2], and can occur in-plane or through-plane [3]. In MRI, motion in the scanned object alters acquired raw data/k-space in ways that differ based on various sampling patterns and motion types. For instance, translation motion changes the phase of k-space, while the rotation of the object leads to a rotation in k-space [4].

Various motion correction techniques have been developed, classified into navigation-based, retrospective, and prospective methods. Among these, the self-navigation technique PROPELLER[5] has gained popularity. PROPELLER not only measures in-plane translation and rotation but also effectively rejects data indicative of through-plane motion. However, its application to cartesian data necessitates a higher sampling requirement, posing a limitation.

The Golden-angle Cartesian Randomized Time-resolved (GOCART)[6] acquisition stands out as a highly accelerated cartesian sampling scheme, demonstrating exceptional performance in Dynamic Contrast-Enhanced (DCE) MRI. Despite its advantages, there exists a noticeable gap in the literature concerning the investigation of artifacts specific to GOCART brain MRI.

In response to this gap, our study introduces a simulation framework meticulously crafted to evaluate the efficacy of PROPELLER correction on translational motion within GOCART-sampled data. We simulated translational motion along two directions and varied motion frequencies, exploring diverse temporal resolutions for the sliding temporal window in k-space. This simulation platform emerges as a pivotal tool for pre-clinical testing, offering a unique avenue for the optimization of motion correction algorithms. By addressing the nuanced challenges posed by translational motion in GOCART-acquired brain MRI, our study contributes valuable insights to the enhancement of imaging protocols and, consequently, the diagnostic reliability of this advanced imaging modality.

2. Methods

2.1. Motion simulation

We employed a T1-weighted image of a single slice from BrainWeb as the stationary image for motion simulation. The in-plane spatial resolution was set at 1 x 1 mm², with a slice thickness of 1 mm, and a matrix size of 217 x 181. The motion simulation steps are indicated by the blue rectangles in the flowchart (Figure 1). Initially, a Fourier transform was performed to generate the stationary k-space. Using the shift property of Fourier Transform, translation motion was introduced by applying a phase along both ky and kz through a sine function with an amplitude of 5 pixels. Motion periods (T) ranging from 2 to 20 seconds, in increments of 2 seconds, were employed to simulate various motion frequencies. The phase encoding order followed a predefined GOCART sampling scheme with an undersampling rate of 30%. The repetition time (TR) was set at 5 ms, resulting in a motion-corrupted composite image.

2.2. Motion correction

The motion correction steps are identified by red rectangles in Figure 1. A temporal sliding window was employed to partition GOCART-sampled data, testing temporal resolutions from 0 to 10 seconds with a temporal step of 1 second. Within each temporally windowed k-space data, the central region of the k-space was extracted as a low-frequency region for translation correction. The central region is the fully sampled k-space region. Cross-correlation was computed between each segmented image and the reference image, obtained from the Fourier transform of an average complex k-space across all segmented k-space data. Phases were then estimated by identifying the peak of the cross-correlation image for the y and z directions. To enhance estimation accuracy, sinc interpolation was applied along the y or z direction prior to locating the peak. The estimated phase for each segmented image was subsequently applied to the corresponding k-space, resulting in the motion-corrected composite k-space/image.

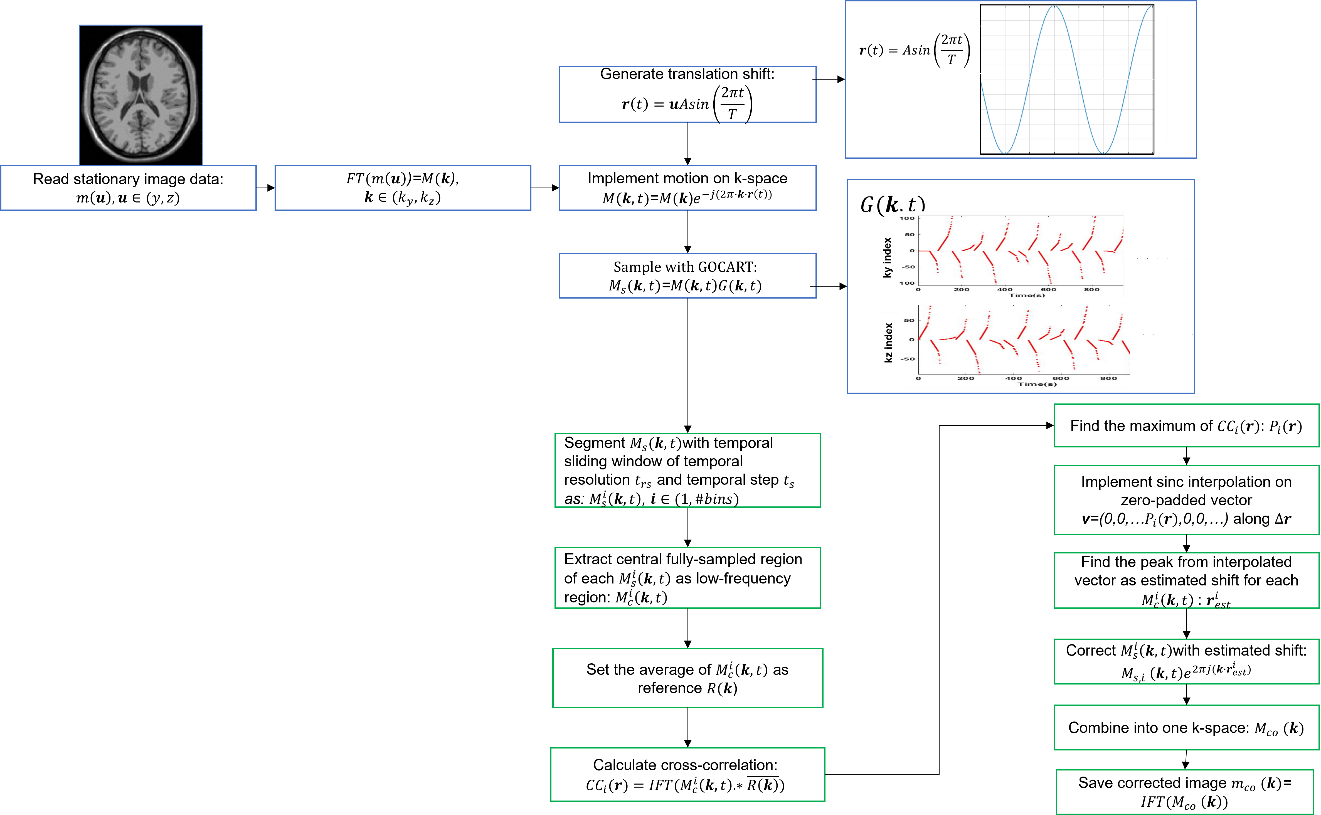
Figure 1. Flowchart of motion correction simulation. The simulation is divided into two parts. The first part is the simulation of translation motion indicated by blue rectangles, and the second part, motion correction, is achieved by estimating the cross-correlation between reference image and each segmented/bin image from GOCART sampling data.

To analyze the correction performance across different temporal resolutions of sliding windows and various motion frequencies, the Normalized Root Mean Square Error (NRMSE) was calculated between the reference stationary image (m) and each corrected image (m_co) across all pixels by

$NRMSE=\frac{{||{m_{co}}-m||_{2}}}{{||m||_{2}}}$

where ${||{m_{co}}-m||_{2}}$ represent the Euclidean norm of the difference between the corrected image and the reference image, and ${||m||_{2}}$ represents the Euclidean norm of the reference image.

3. Results

In Fig. 2, the anatomical map illustrates the reference stationary image, motion-corrupted image, and the corresponding motion-corrected images. Notably, higher-frequency motion (8s) induces more severe distortions compared to lower-frequency motion (12s), evident in Fig. 2 (b) and (e). Corrected images at temporal resolutions of 4 and 8 seconds for the sliding window are presented in Fig. 2 (c) and (d), respectively, while (f) and (g) represent the same temporal resolutions for the higher-frequency corrupted image (e). The correction performance is notably less effective in the presence of higher-frequency motion distortions compared to lower-frequency counterparts. Intriguingly, the lower temporal resolution (8 seconds) does not outperform the higher temporal resolution, despite its inclusion of more spatial information for motion estimation.

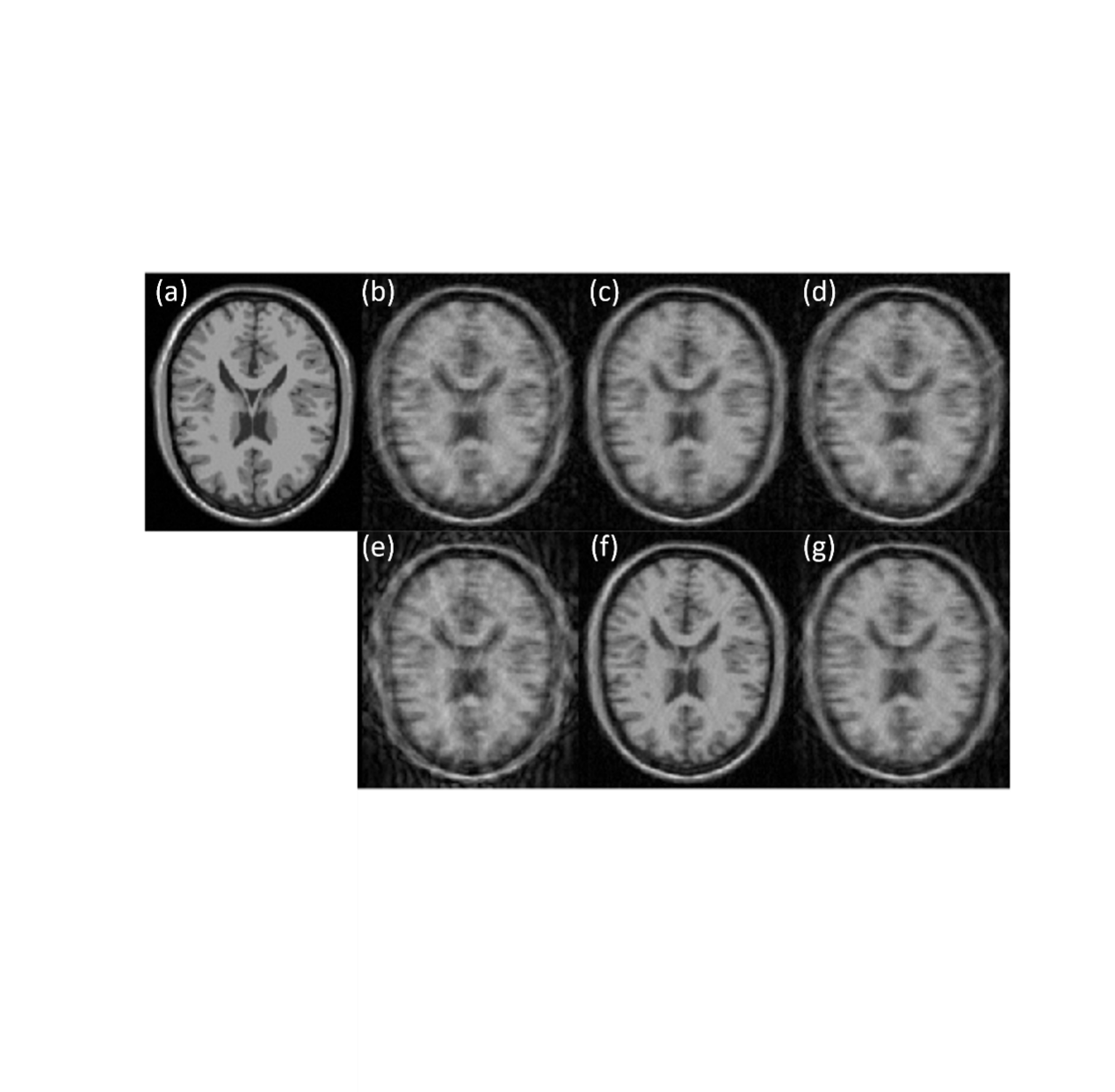
Figure 2. (a) Stationary image. (b) and (e) are simulated motion-corrupted image with motion period of 12 and 8 seconds, respectively. (c) and (f) are motion corrected image with temporal window resolution of 4 seconds; (d) and (g) are the correct image with resolution of 8 seconds.

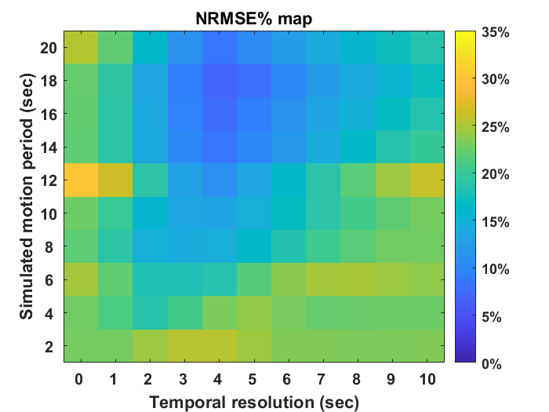
Figures 3 and 4 depict NRMSE maps and plots, illustrating the correction performance at various temporal resolutions for motion-corrupted images with different motion periods/frequencies. Lower temporal resolutions demonstrate improved correction, attributed to a higher density of k-space points acquired in one temporal bin, facilitating better motion estimation with higher spatial resolution. However, extremely low temporal resolutions (>5 seconds) introduce more motion contamination in the k-space, hindering effective correction despite the availability of enhanced spatial information. This limitation is evident in the NRMSE plot, marked by a distinct valley. Furthermore, slower motion frequencies are more effectively corrected, aligning with expectations due to the reduced motion among low-frequency images.

0

Figure 3. NRMSE Map Between Stationary and Corrected Images. Column 0 displays the non-corrected result, while Columns 1 to 10 present corrected results representing different bin temporal resolutions. Each row corresponds to a simulated motion period.

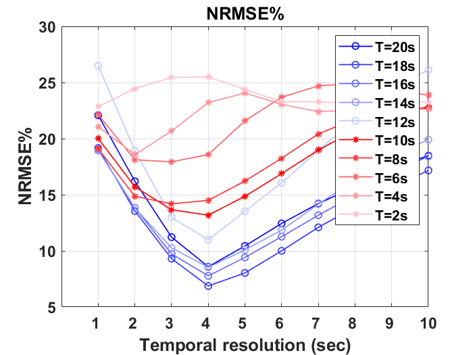
Figure 4. NRMSE Plot. Each line represents different motion periods, and the x-axis indicates the temporal resolution for each temporally segmented bin.

4. Conclusion

In conclusion, this study thoroughly examined the impact of translational motion on brain MRI by employing a simulation framework and motion correction techniques. The application of PROPELLER correction on GOCART-sampled data revealed significant variations in correction performance influenced by both motion frequency and temporal resolution. Notably, lower temporal resolutions (ranging from 3 to 5 seconds) demonstrated improved correction, benefiting from the increased density of k-space points within each temporal bin and thereby providing higher spatial resolution for motion estimation. Conversely, excessively low temporal resolutions (>5 seconds) posed challenges associated with motion contamination in the k-space, thereby limiting effective correction despite the enhanced spatial information. Notably, faster motion (<0.1 seconds) imposed constraints on correction performance, exceeding a threshold of >10% error, irrespective of the employed temporal resolution.

However, it is essential to acknowledge certain limitations within this study. Primarily, only rigid translation in-plane motion, such as rotation, was simulated for the GOCART sampling pattern, potentially limiting the generalizability of the findings. Future work should encompass a broader range of motion types to provide a more comprehensive understanding. Another notable limitation is that multi-slice data should be considered to address potential through-plane motion, which is a common occurrence in brain MRI.