1. Introduction

The internet has become a ubiquitous presence in modern life, serving as both a platform for entertainment, including online shopping, video streaming, and gaming, and a tool for technical tasks such as data processing, programming, and financial analysis. With the vast user base and extensive content, personalizing information for individual users has emerged as a critical challenge. Such challenges are categorized as multi-armed bandit problems [1]. There is a plethora of algorithms aimed at solving these problems, and significant advancements have been made by researchers. For instance, Regularized Thompson Sampling and the Greedy Algorithm have been effectively applied in multi-armed bandit scenarios for dose-finding in clinical trials due to their superior selection performance [1]. Dakdouk Hiba and his team developed the Decreasing-Order-Fair-Greedy algorithm, enhancing performance in Internet of Things (IoT) networks, specifically in Long-Range (LoRa) networks, representing a significant improvement over the Adaptive Data Rate (ADR) algorithm [2]. Additionally, a dynamic combinatorial multi-armed bandit (DCMAB) learning approach was introduced for selecting multi-hop relays in underwater acoustic sensor networks, which efficiently addresses the challenge of learning inefficiency due to sparse information on newly-formed links and achieves minimal propagation delay without prior channel information [2]. In the realm of 5G Massive MIMO, a combinatorial multi-armed bandit (CMAB) strategy was utilized to devise methods for user scheduling and spectrum allocation [3]. Similarly, in Mobile Crowd Sensing (MCS), the multi-armed bandit approach has been adopted for recruiting unknown workers based on credit and quality, leading to the development of a two-stage reward-based Multi-Armed Bandit and a unique credit identification algorithm, enhancing worker selection in reverse auctions [3].

Despite the proliferation of these applications, comparative studies of different algorithms' performance remain scarce, potentially leading to confusion among users about which algorithm best meets their needs. This paper addresses this gap by comparing the performance of five distinct algorithms, focusing particularly on their application contexts. Utilizing the Movie Lens dataset, this study examines the mean regret of each algorithm as an evaluation criterion for their performance, aiming to provide insights that could guide future research [4].

The Movie Lens dataset, essential for this analysis, comprises 18 different movie genres, each assigned a numeric code from 0 to 17. Ratings in this dataset are integers from 1 to 5, with 1 indicating the lowest rating. For the purpose of this study, each movie genre is treated as an "arm," and the corresponding rating as the "reward." This setup remains consistent throughout the paper.

2. Brief introduction to the algorithms

2.1. ETC algorithm

Just as the name of this algorithm, it can be divided into two stages. The first one is Exploration Phase. In this stage, the algorithm will try to explore all the choices (arms) to collect the reward of each arm. Usually, the algorithm will choose the arms randomly or follow a certain strategy such as uniform distribution [5]. The aim of this phase is to acknowledge the potential reward of each arm as more as possible, in order to make wiser decisions in the coming phase. The second stage is Commit Phase. After the Exploration Phase, the algorithm will choose a “best” arm, which is often determined by the mean reward or other statistical quantity according to the information collected before. It is important to point out that once the “best” arm is selected, the algorithm will always choose this arm in the following choices instead of exploring other arms.

Though ETC algorithm is simple and intuitive, it has some limitations. For example, if the Exploration Phase is not long enough or distribution of the rewards changes too fast, the algorithm may not find the “best” arm. Moreover, during the Commit Phase, the algorithm will fail to adapt when the rewards of other arms change as it no longer makes explorations.

2.2. UCB algorithm

The main idea of UCB algorithm is to estimate each arm’s value and then, choose the arm with the highest upper confidence bound. The operational principle of UCB algorithm consists two parts: the mean reward obtained of all the past operations and a term associated with the level of exploration [6]. In specific, this term is usually calculated based on the horizon of the operation and the logarithm of the amount of the total operations. In this case, the value not only takes the historical performance of the bandit into consideration, but also makes aware of the uncertainty of the bandit.

The UCB algorithm successfully achieved a balance between exploration and exploitation, which effectively avoids excessive exploration or exploitation. Moreover, it doesn’t need prior modeling of the environment, so it can be used in circumstances with high uncertainty. Due to its advantages, this algorithm is used in many areas. The logistics planning with an exploration and exploitation structure uses a novel two-stage dynamic pricing model: A multi-armed bandit problem used UCB algorithm to make price optimizations in order to address the issue of dynamic pricing, which needs to both maximize revenue and learn the demand function.6

2.3. TS algorithm

The process of TS algorithm is a bit more complex. Firstly, establish a probability distribution model for each possible arm, typically using Beta Distribution. In the initial stage, if there is no prior knowledge, these distributions can be set as uniform distributions. Then, the algorithm begins the iterative process [7]. In each iteration, the algorithm generates a random sample value for the Beta Distribution of each arm. This random value can be seen as an estimate of the potential value of the option. Next, the algorithm selects the option with the maximum random sample value for execution. After executing the arm, the Beta Distribution of the corresponding arm based on the observed reward will be updated. If a reward is obtained, increase the probability of success (the value of α). If losses are incurred, increase the probability of failure (the value of β). By continuously updating the Beta Distribution and resampling, the algorithm can gradually approach the true value of each arm and find a middle ground between exploration and exploitation.

Due to the characteristics of Beta Distribution, when a certain arm has a good historical performance, its random sample value is more likely to be larger, thus being selected more frequently. Meanwhile, due to the presence of randomness, the algorithm also has the opportunity to explore other options to avoid falling into local optima [8].

It is noted that the TS method is used to a collection of search and optimization "bandits" in Multi-armed bandits, Thomson sampling, and unsupervised machine learning in phylogenetic graph search in order to favor fruitful search strategies [9]. Without any prior understanding of the attributes of the phylogenetic datasets, this technique functions as a type of unsupervised machine learning.7 The superiority of TS algorithm is also proved in Bandit algorithms: A comprehensive review and their dynamic selection from a portfolio for multicriteria top-k recommendation. They argue that TS algorithm makes better selections than the original EXP3 method when it comes for Multiple-play Gorthaur.8.

2.4. Epsilon-Greedy algorithm

The core idea of Epsilon-Greedy algorithm is to set a probability Epsilon, and at each time step or decision point, the algorithm explores with the probability of Epsilon and exploit with a 1-Epsilon probability. Specifically, when the algorithm decides to explore, it ignores the current estimates and rewards and randomly selects an action [10].

This randomness helps to discover excellent actions that may not be noticed, as it neither misses opportunities to discover better actions due to being too conservative, nor frequently attempts ineffective actions due to being too risky.

3. System analysis on each algorithm

3.1. ETC algorithm

To make the results have more credibility, this passage choose the horizon as n=100,000 and set the length m*k of the exploration phase as 10% of n, which means m*k=10,000. The cumulative regret run by ETC algorithm is recorded as the criteria to judge the performance of the algorithm. To avoid extreme situations, this process is repeated 10 times, reshuffling the data each time before the experiment is run. The result is as shown in figure 1.

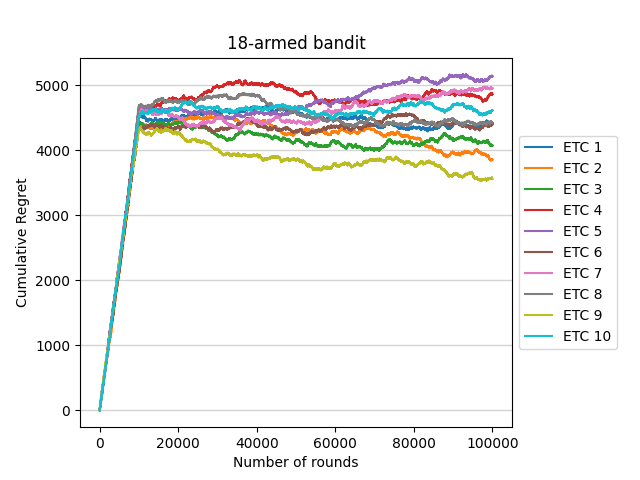
Figure 1. 18-armed bandit (Photo/Picture credit: Original).

Then, with the same setting, the process is repeated for 100 times and plot the average regret together with error bars indicating one standard deviation above and below the mean as shown in figure 2.

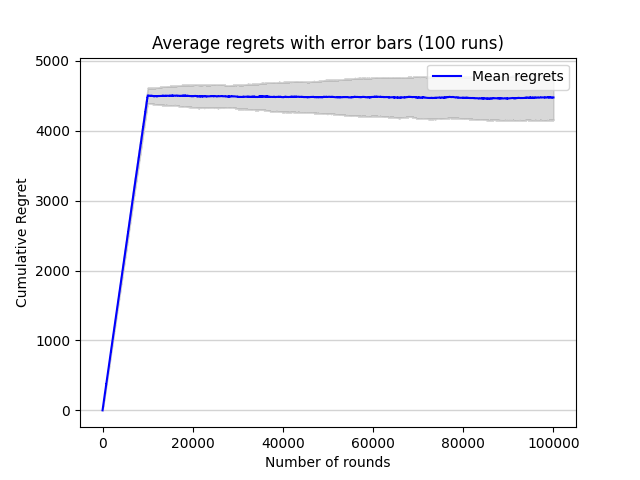
Figure 2. Average regrets with error bars (100 runs) (Photo/Picture credit: Original).

The two plots above illustrate that the cumulative regret of ETC algorithm will become larger but finally get stable as the horizon gets larger.

3.2. UCB algorithm

To ensure the comparability of different algorithms in the following part of this passage, the horizon is set as n=100,000, which is the same as ETC algorithm. The UCB index for arm i at round t-1 is set as

where B is the difference between the maximum possible reward value and the minimum possible reward value. As in the Movie Lens dataset where rewards can be in the interval 1-5, B should be set as 4. As in the previous ETC algorithm, run ten experiments and record the cumulative regret of the UCB algorithm at each round t=1, 2, ..., n in all experiments. The result is as shown in figure 3.

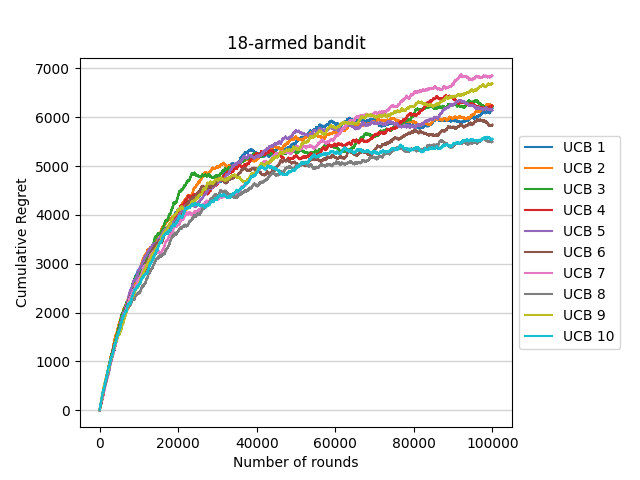
Figure 3. 18-armed bandit (Photo/Picture credit: Original).

Also, the result that the experiment is repeated for 100 times and also with error bars indicating one standard deviation above and below the mean is as shown in figure 4.

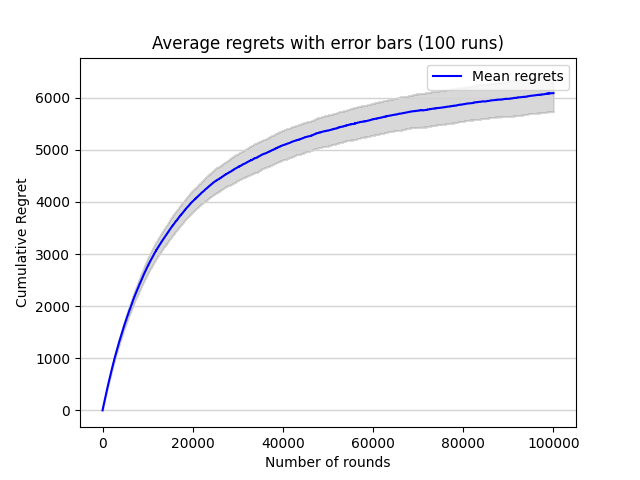
Figure 4. Average regrets with error bars (100 runs) (Photo/Picture credit: Original).

The two plots indicate that the cumulative regret of UCB algorithm will continuously get larger without stop while the horizon gets larger.

3.3. TS algorithm

For this algorithm, the horizon is still n=100,000. The difference is that the algorithm is initialized by choosing each arm once. In other words, for the first k rounds, arm1, arm2, ... , arm k are chosen respectively. Then, the distributions Fi(t), i=1, ..., k for the belief on the mean rewards of arms are updated as follows:

, t=k+1, ...

is the average reward of arm i until round t, B is the same as above for the UCB algorithm, Ti(t) is the number of samples received from arm i until round t, and N (μ, sigema2) stands for the Gaussian distribution with mean miu and variance sigema.

With this setting, 10 experiments are run and the result is as shown in figure 5.

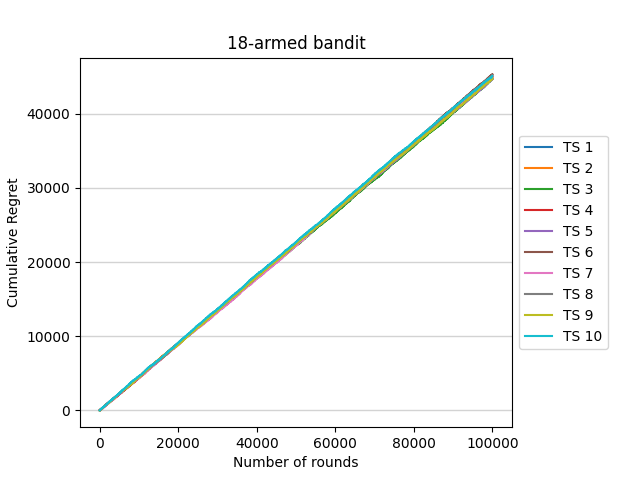
Figure 5. 18-armed bandit (Photo/Picture credit: Original).

Then again, 100 experiments are run and plot the average regret together with error bars indicating one standard deviation above and below the mean as shown in figure 6.

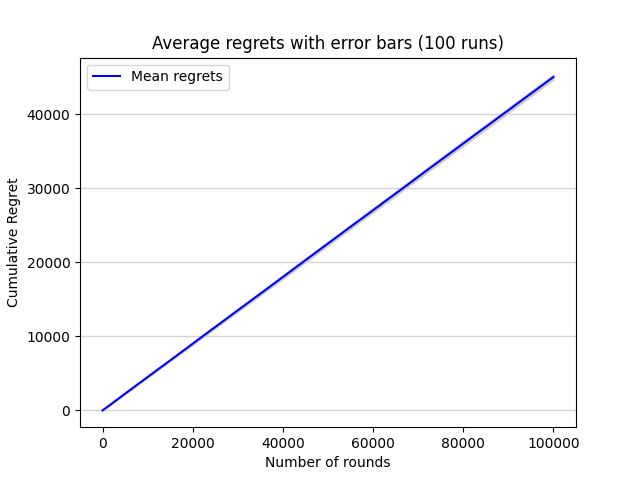
Figure 6. Average regrets with error bars (100 runs) (Photo/Picture credit: Original).

As the error bars are relatively too small compared with the values of the cumulative regret, they can’t be seen clearly. So part of the plot is chosen and enlarged, making error bars clearer to be seen as shown in figure 7.

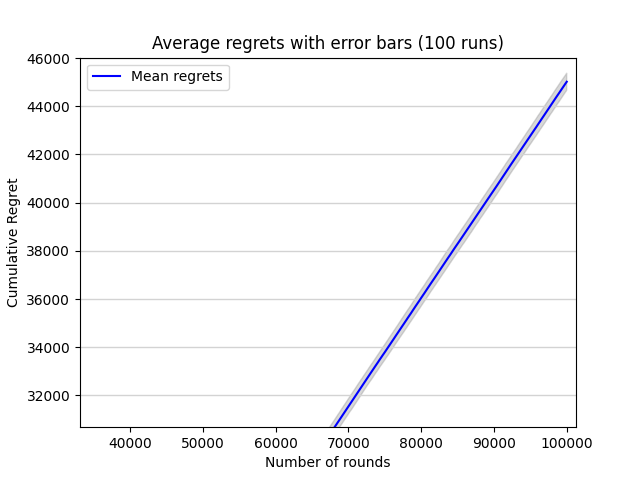
Figure 7. Average regrets with error bars (100 runs) (Photo/Picture credit: Original).

3.4. Epsilon-Greedy algorithm

Except that the value of horizon is still n=100,000, in this particular algorithm, the value of Epsilon is firstly set as 0.1. Due to its speciality and simplicity, this passage only run one experiment as shown in figure 8.

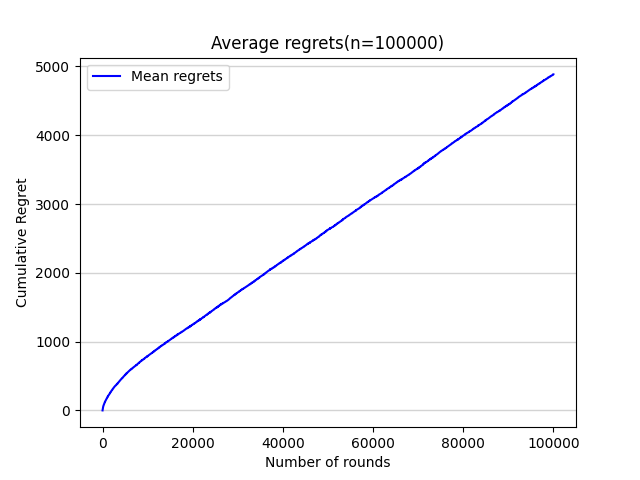
Figure 8. Average regrets(n=100000) (Photo/Picture credit: Original).

Then, this passage adds the annealing Epsilon-Greedy algorithm, which means the value of Epsilon is no longer a constant. With other settings remain the same, the result is as shown in figure 9.

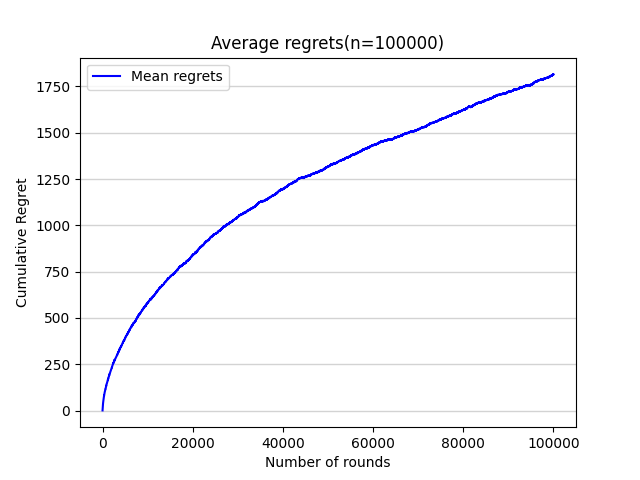
Figure 9. Average regrets(n=100000) (Photo/Picture credit: Original).

3.5. Comparison among algorithms

To make sure the reliability, in this part, all horizons of algorithms are set to 1,000,000 while other settings remain the same. The result based on Python is as shown in figure 10.

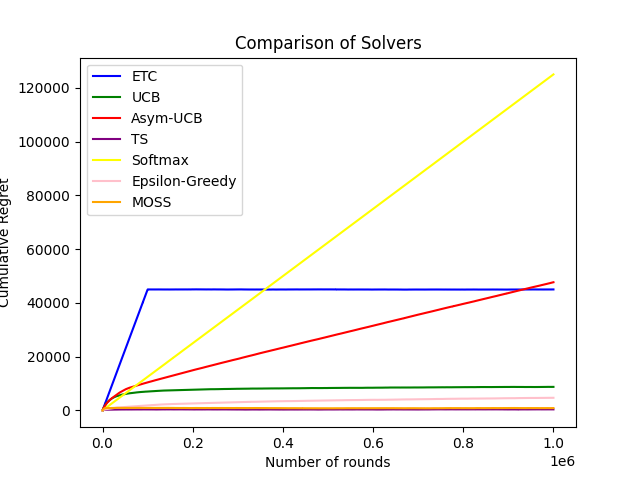
Figure 10. Comparison of Solvers (Photo/Picture credit: Original).

From this plot, it is obvious that ETC algorithm has the largest cumulative regret no matter how large the horizon is, which in other words means that ETC algorithm has the worst performance among the 4 algorithms mentioned before. Then comes UCB algorithm, whose cumulative regret is much smaller than ETC algorithm, but still quite large compared with other two algorithms, making it the second worst algorithm. As the performances of TS algorithm and Epsilon-Greedy algorithm can’t be seen clearly in Picture 10 above, a experiment is run without the ETC algorithm and Softmax algorithm, which is a whole new algorithm not mentioned in this passage for it has little applications in real world life. The result of the new experiment is as shown in figure 11.

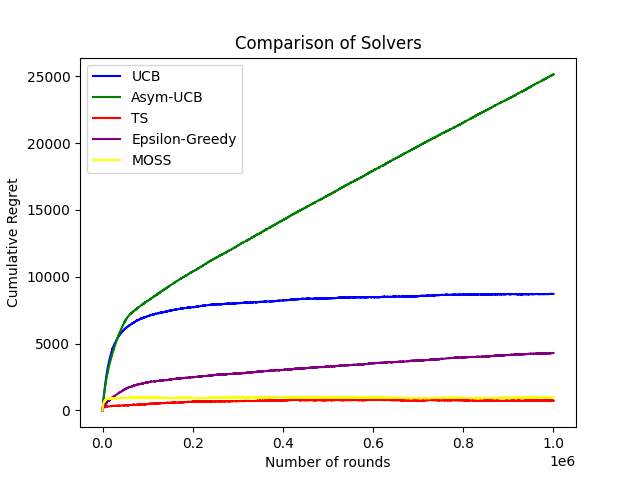
Figure 11. Comparison of Solvers (Photo/Picture credit: Original).

From this plot, it can be seen clearly that TS algorithm (the red line) has the least cumulative regret among multiple algorithms, indicating that it has the best performance.

It is noteworthy that Picture 10 also mentions some other algorithms such Softmax algorithm and MOSS algorithm, and the sub algorithm of UCB algorithm (asymptotically UCB algorithm) is also taken into consideration. By adding these algorithms, this passage hopes to provide a diversified comparison between algorithms instead of merely focusing on the main ones. This also means that some algorithms have yet to be proposed when facing new bandit problems. The suggested Seq meta-algorithm offers the same theoretical guarantees as the MAB policy used in adapting bandit algorithms for settings with sequentially available arms, but it was demonstrated to provide better performance when compared to several classical MAB policies in RM and BAI problems using real-world data.9 Moreover, some existing algorithms need special improvement to better adapt to the real-world situation. A novel version of INF, known as the Implicitly Normalized Forecaster with clipping (INF-clip), was proposed in Implicitly normalized forecaster with clipping for linear and non-linear heavy-tailed multi-armed bandits for MAB problems with heavy-tailed reward distributions.10

4. Conclusion

This study delves into the multi-armed bandit problem and reveals significant performance disparities among different algorithms under identical conditions. Through experiments conducted in Python and illustrated by the accompanying plots, it is evident that the Thompson Sampling algorithm outperforms others, exhibiting the least cumulative regret, while the Explore-then-Commit algorithm shows the poorest performance, with its cumulative regret substantially exceeding that of its counterparts. This analysis addresses a gap in comparative studies of multiple algorithms, providing valuable insights for organizations uncertain about selecting the most effective algorithm. The visual representations facilitate a clearer understanding of each algorithm's performance, aiding decision-makers in choosing the most suitable option. Furthermore, this work establishes a framework for subsequent research into additional algorithms for solving multi-armed bandit problems. However, this study is constrained by its reliance on a single dataset and the examination of only four principal algorithms. Future research should expand the dataset range to enhance the robustness of these comparisons. Moreover, inclusion of more specialized sub-algorithms, such as the asymptotically optimal UCB algorithm, is crucial to ensure a comprehensive evaluation of available strategies.