1. Introduction

Over the last decades, it has become a tendency that a great number of scientists are prone on ferreting a new kind of energy that can replace the significant position of traditional non-regenerated energy resource like nuclear power, gas, and coal for the purpose of satisfying the requirement of the sustainable development. Wind power assumes an increasingly foundational role as a prominent component within the spectrum of sustainable energy sources. Nevertheless, the vigorous character of wind contributes to significant intermittency, randomness, and uncertainty to wind power generation [1, 2]. The integration of wind power on a large scale into the grid poses substantial disputes to the cautious and persistent functioning. Thus, the precise forecast of wind power is the one of the most critical components of operating wind power in the view of its significance in optimizing the efficiency and reliability of renewable energy integration into the electrical grid infrastructure. Nowadays, as the technique and technology advances by leaps and bounds, wind power prediction has been undergoing a rapid development in recent years.

This essay will compare the accuracy of three modern basic algorithm, which is Grey Wolf Optimization( GWO), Grey Model and Sparrow Search Algorithm (SSA) respectively, by observation of mean-square error (RMSE) ,mean absolute error (MAE), , and mean absolute percentage error (MAPE) of system consisted of reinforced algorithm and machine ,such as variational mode decomposition (VMD) and an extreme learning machine (ELM) optimized by an improved grey wolf optimization (GWO), and analysis the reason of the final result in the terms of the main characteristic of origin model. The elementary intention of this research is to discern the most effective algorithm among Grey Wolf Optimization (GWO), Grey Model, and Sparrow Search Algorithm (SSA) in the context of optimizing wind power prediction accuracy. Furthermore, the aim is to elucidate methodologies for enhancing the precision of these algorithms to a considerable extent, thereby ensuring the robust operation of large-scale grid connections. Besides, the improved wind power prediction can result in other benefits like grid stability, integration of renewable energy, market Operations, reduction of system costs and mitigation of environmental Impacts: For example, precise forecasts enable market participants to make informed decisions regarding energy trading, scheduling, and pricing. This promotes market efficiency and transparency, benefiting both producers and consumers. Aside from that, more precise predictions can lead to cost savings for both energy producers and consumers. Energy producers can optimize their operations, reducing the need for costly backup power or inefficient ramping up/down of conventional power plants. Consumers may also benefit from more stable energy prices because of improved grid management. Then by maximizing the utilization of wind energy, greenhouse gas emission and fossil fuels is capable of being dwindled by individuals with the purpose of mitigating climate change. This contributes to a cleaner environment and helps in achieving sustainability goals, and Accurate predictions allow for more efficient energy trading in wholesale markets. Energy traders can make better-informed decisions regarding buying and selling electricity, leading to improved market efficiency and potentially lower costs for consumers.

2. Basic Principles and Methods

2.1. Grey Wolf Optimization (GWO)

2.1.1. Definition of GWO Model

A heuristic enhancement technique that draws inspiration from the collective behaviors observed in grey wolf packs is the Grey Wolf Optimization (GWO) algorithm. Wolf populations in nature. It simulates the collaborative and competitive behaviors of a grey wolf pack when solving problems, optimizing solutions by mimicking the foraging behavior of grey wolves. The figure 1 delicate how the algorism can serve a purpose in limited procedure. The fundamental idea of the algorithm is to treat the solution space of a problem as a grey wolf ecosystem, where the positions of grey wolves represent solution positions, and their fitness represents the quality of the solutions. The algorithm updates the positions of grey wolves by simulating four behaviors in the wolf pack (searching, encircling, chasing, and escaping) to find better solutions [3]. The flowchart of GWO is shown in figure 1.

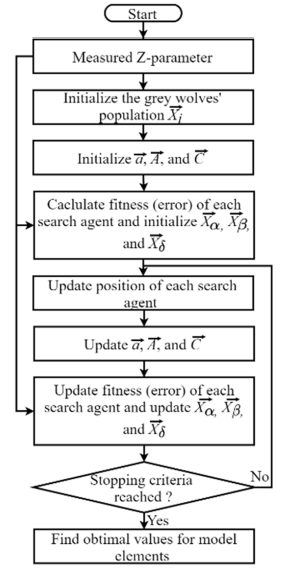
Figure 1. Flowchart of GWO (Picture credit: Original)

2.1.2. Relevant formula about model

In devising the Grey Wolf Optimization (GWO) algorithm, a mathematical framework is established to depict the social structure within wolf packs, wherein the optimal solution is denoted as α. Additionally, the 2nd and 3rd optional explication are labeled as β and δ correspondingly. The residual potential solutions are represented by ω. In the GWO algorithm, the chasing dynamics are influenced by α, β, and δ, with ω coyotes trailing behind leaders. There are three distinct phases in the entire system, which is divided to surrounding, hunting, and attacking.

Firstly, a consortium of wolves systematically encircles its target, the definition of their behavior is following.

D= \( |C\cdot {X_{p}}(t)-X(t)| \) (1)

X \( (t+1) \) = \( {X_{p}}(t)-A\cdot D \) (2)

Equation (1) depicts the outstrip between the individual and the prey, while formula (2) illustrates the position update formula for the grey wolf. In this context, D denotes the wolf’s new status vector, and t represents the current iteration. Additionally, \( X(t) and {X_{p}}(t) \) designate status transmitter for the target and the hyenas respectively. The relevant calculation prescription of A and C are provided below. A and C exemplify the collaborative courses, and follows is their equations are: `

\( {r_{1}}\cdot 2a-a =A \) (3)

\( {r_{2}} =\frac{C}{2} \) (4)

The vector a range from [2, 0] throughout iterations, while \( {r_{1}} \) and \( {r_{2}} \) are vectors with random values between 0 and 1, respectively.

Secondly, the grey wolves can identify the prey's location and strategically encircle them. Once the grey wolves ascertain the prey's position, β and \( δ \) , guided by \( α \) , lead the wolf pack in surrounding the prey. The model concerning the orientation of math for the grey wolf's stalking of prey location can be summarized as follows.

\( D=C\cdot X-{X_{Current}} \) (5)

Here, D display each distance from other individuals; \( X \) denote the current positions; \( C \) are arbitrary carriers, and X represents the contemporary location of dingoes.

\( X \) = \( X-A\cdot (D) \) (6)

\( X(t+1)=0.33{Σ(X_{1}}+{X_{2}}+{X_{3}}) \) (7)

Equation (6) delineates the magnitude and direction of the individual movement step for the ω entity within the wolf pack, directed towards α, β, and δ respectively. Equation (7) establishes the ultimate situation of ω.

The final phase is the attacking stage. When the absolute value of the coefficient is less than 1 (| | < 1), the wolves initiate an attack on the prey, often resulting in converging towards a local optimum. Conversely, whereas the unqualified value of the coefficient is higher than 1 (| | > 1), the bolt breaks away from the casualty, aiming to locate a more optimal prey target, typically associated with the global optimum [4].

2.2. Grey Model

2.2.1. Definition of Grey Model

Grey prediction corresponds to foretelling approach that leverages limited incomplete information to construct mathematical models for prediction. It relies on past and present developmental trends of objective phenomena, employing scientific methodologies to depict and analyze future trends and conditions, forming scientific hypotheses and judgments.one of the usual example is that the application concerning on the forecasting wind power, wind power generation systems may seem irregular, so they can be treated as a grey system for research. The grey system requires minimal historical data for prediction, has an understandable model, and provides high prediction accuracy without sacrificing simplicity in computation. It also has the advantage of not considering distribution patterns.

Grey prediction models are effective for predicting data sequences with very few (e.g. Only 4) and Insufficient data integrity and reliability. thoroughly investigate the essence of the data., Requiring minimal information for modeling, leading to high accuracy, computational simplicity, ease of verification, and negating the necessity to consider distribution patterns or trends changes. However, grey prediction models are generally only befitting for short-term predictions. Furthermore, it is best suited for exponential growth predictions, such as population numbers, flight numbers, water consumption predictions, industrial output predictions, etc.

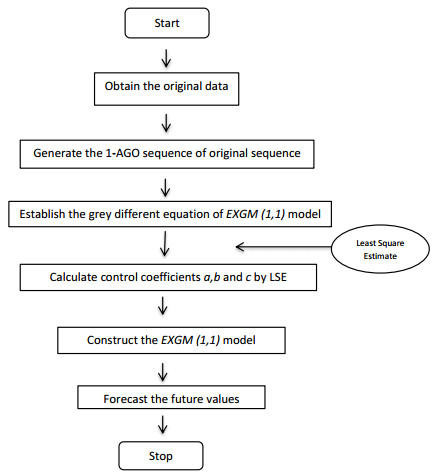
Figure 2. the flowchart of grey model (Picture credit: Original)

2.2.2. Relevant formula about grey model

In math, the modeling process of a grey system is mainly implemented through the following formulas:

1. Grey Autoregressive Model (GM (1,1))

\( [X(t)]=X(t-1)a-(1-a)(1-t)X \) (8)

Where X(t) demonstrate the system's current state at time t, a belong the grey coefficient, with values between 0 and 1, indicating the degree of uncertainty in the system.

2. Grey Prediction Model (GPM):

\( X(t+1) \) = \( aX(t)+(1-a)X(t) \) (9)

2.3. Sparrow Search Algorithm (SSA)

2.3.1. Definition of SSA

SSA, stimulated by the rummaging and anti-carnivore conduct of passerines, stands as a swarm intelligence optimization algorithm. In contrast to conventional multitude intelligence optimization algorithms, it distinguishes itself through remarkable search precision, rapid convergence, elevated stability, and robust parallelism. Despite its underdeveloped advancement and practical utilization, SSA harbors significant prospects and research potential.

2.3.2. Relevant formula about SSA model

The behavior of sparrows is quite complicated due to it can be affected by multiple unknown factors like environment, rival, and mate etc. With aims of predicting their behavior exactly, a series model is following:

1.The position of sparrows can be expressed by using matrix.

\( [\begin{matrix}{X_{n,1}} & {X_{n,2}} & ... & ... & {X_{n,d}} \\ \end{matrix}] \) (10)

N is on behalf of the count of bird; d denotes the figure of magnitudes of the capricious to be ameliorated

2.The physical condition values of entire dissimilar sorts of sparrows can then be represented with the transmitter below

\( [\begin{matrix}f([{X_{n}} & {X_{n,2}} & ⋯ & ⋯ & {X_{n,d}} \\ \end{matrix}] \) (11)

Within the SSA framework, precedency for acquiring forage resources pending the rummage process is given to producers with superior fitness values. Additionally, fabricator, responsible for both food search and population flow, have a broader search range compared to moochers. During every period of iteration, the update of sparrow’s position is following:

\( X_{ij}^{t+1} \) = \( \begin{cases} \begin{array}{c} X_{ij}^{t}\cdot exp\frac{(-i)}{α\cdot {inter_{max}}}if{ R_{2}} \lt ST \\ X_{ij}^{t}+Q\cdot L if { R_{2}}≥ST \end{array} \end{cases} \) (12)

Another type of sparrow functions as a scavenger, adhering to rules (4) and (5). Certain scavengers regularly monitor producers, swiftly relocating to compete for discovered food upon witnessing a producer's success. If successful, they claim the food immediately; otherwise, they persist in following the established rule.

\( X_{ij}^{t+1} \) = \( \begin{cases} \begin{array}{c} Q\cdot exp\frac{(X_{worst}^{t}-X_{ij}^{t})}{{i^{2}}} if i \gt \frac{n}{2} \\ X_{p}^{t+1}+|X_{ij}^{t}-X_{p}^{t+1}|\cdot {A^{+}}\cdot L otherwise \end{array} \end{cases} \) (13)

\( X_{ij}^{t+1} \) = \( \begin{cases} \begin{array}{c} X_{best}^{t}+β\cdot |X_{ij}^{t}-X_{best}^{t}| if {f_{i}} \gt {f_{g}} \\ X_{ij}^{t}+k\cdot (\frac{|X_{ij}^{t}-X_{worst}^{t}| }{({f_{i}}-{f_{w}})+ε}) if {f_{i}}={f_{g}} \end{array} \end{cases} \) (14)

3. Analysis of the effect of algorithm application

3.1. Improved GWO algorithm

3.1.1. The theoretical basis of improved GWO algorithm

Over the past four years since 2020, various enhanced applications of the Grey Wolf Optimization (GWO) have been developed, aiming to enhance the correctness of augury of wind power and optimize the exertion of wind energy. This essay explores a prediction model that integrates Variable Mode Decomposition (VMD) and an improved intelligent optimization algorithm, alongside another approach that combines Variational Mode Decomposition (VMD) with an Extreme Learning Machine (ELM) optimized by an enhanced Grey Wolf Optimization (GWO) algorithm with aims of foretelling wind power. Additionally, a novel prediction model is proposed, merging Grey Wolf Optimization (GWO) with a Bidirectional Long Short-Term Memory Network (Bi-LSTM).

The theoretical enhancements and modifications introduced in improved versions of the GWO algorithm aim to address the algorithm's limitations, enhance its performance characteristics, and expand its applicability to a diverse selection of escalation conundrums. These improvements are often validated through empirical studies, benchmarking against standard test functions, and real-world applications to demonstrate their effectiveness and superiority over the original algorithm.

3.1.2. The effect of using improved GWO algorism.

In 2020, Jiale Ding introduced prediction model that utilizes variational mode decomposition (VMD) and an extreme learning machine (ELM) optimized through an enhanced GWO algorithm for wind power in a brusque term [5]. The performance evaluation of this VMD-improved GWO-ELM model revealed a RMSE of 5.9113%, MAE of 4.6219%, and MAPE of 13.01%. These metrics surpass those achieved by ELM, backpropagation (BP), and the improved GWO-ELM model. Through simulations, it was observed that this contemplated paradigm yields superior accuracy in prophecy of short-term wind power compared to alternative models.

Two years subsequent to 2020, Zhu Changsheng and Zhao Kuipeng introduce a model that integrates Variable Mode Decomposition (VMD) and Enhanced GWO to maximie the Kernel Extreme Learning Machine (KELM) [6]. The final experimental results indicate a diminution in both the RMSE and MAE to 2.62% and 1.94%, respectively. This marks a decrease of 1.03 percentage points and 0.77 percentage points in RMSE and MAE errors compared to the KELM prediction model. These findings suggest that employing VMD decomposition technology for preprocessing original power data aids in noise reduction, thereby bolstering the precision of wind capicity prediction.

In 2024, Hongbin Sun introduces a predictive model on behalf of presaging short-term wind farm output capacity, which integrates adaptive noise reduction CEEMDAN, GWO, and bidirectional long short-term memory network (Bi-LSTM) [7]. From the experimental data, MAPE, MAE, and RMSE are determined to be 3.29%, 0.301%, and 0.154% respectively. Utilizing the GWO algorithm to upgrade the optimization parameter of the Bi-LSTM model has the potential to enhance its predictive capabilities. Additionally, an improved grey model algorithm is explored.

3.2. Improved grey model algorithm

3.2.1. The theoretical basis of improved grey model algorithm

The improved grey model concludes EMD-based gray combined with divergent foretelling model, GM (1, 1, \( {t^{α}} \) ), GM (1,1), all of them have the characteristics that is not limited by the small number of species.

3.2.2. The effect of using improved grey model algorism.

For the EMD-based gray combined forecasting model. This model is proposed by Minghao Ran [8]. From the following table 1, the MAE, RMSE and MAPE can be showed, and the least MAPE is the DGGM model, which is 4 \( \% \) . The EMD-DGM model demonstrates strong appropriate exactitude in both coaching and divination datasets, exhibiting notable adaptability to cyclic seasonal data patterns.

Then, in 2020, Wind power significantly contributes to global electricity generation. It is increasingly crucial for predict wind turbine capacity to create cleaner production. To address this objective, a novel accumulated GM with prioritized contemporary data and temporal power is introduced for wind turbine capacity prediction in short-term. by Jie Xia [9]. Besides, the RMSE of this grey model is 1.63 \( \% \)

Finally, grey prediction models have been identified as an adaptable technique for wind energy forecasting within uncertain systems. Nevertheless, the conventional model is afflicted by the infrequent occurrence of necessary condition failures. a comprehensive modified GM (1,1) model that is contemplated by Muhammad Uzair Yousuf are amalgamated to overwhelm the points of the orthodox procedure [10]. There are 3 distinct categories of case in the process of prediction error of \( {V_{wind}} \) , which is determined by the valve of \( α \) .In the entire category, the case that \( α \) is equal to 0.9 possess least ME, MAE, MSE and RMSE, which is 0.009684 0.489 0.4282 0.6544 respectively. Moreover, its accuracy rate is 97.67 \( \% \) .

3.3. Improved Sparrow Search Algorithm (SSA)

3.3.1. The theoretical basis of improved Sparrow Search Algorithm (SSA)

The Sparrow Search Algorithm (SSA) offers notable merits such as exceptional search accuracy, rapid convergence, robust stability, and effective parallelism. Improving the accuracy of wind power forecasting holds significant importance in addressing the inherent uncertainty and variability inherent in wind energy. Factors like wind speed and orientation are pivotal in determining the power generation of wind turbines. To address these challenges, three distinct algorithms, namely the Sine Cosine Search-Sparrow Search Algorithm (SSSA), SSA-VMD-SE-SPSA-LSTM algorithm, and SSA with Deep Extreme Learning Machine, have been developed replied on modifications to the SSA approach.

3.3.2. The effect of using optimized Sparrow Search Algorithm (SSA)algorism.

Achieving precise and robust ultrashort-term wind power forecasting is imperative for enhancing management of power quality and reliability while concurrently declining the costs associated with backup supply rotation. In 2024, Qingcheng Lin proposed a model optimized through collaborative algorithmic techniques to portend the power of wind, one of the most outstanding algorithms is sine cosine search-sparrow search algorithm, whose MAE, MSE and RMSE is 0.696 1.237 4.187 respectively [11]. In the end, the algorithm that add SSA have more effect on the decrease of the error.

Wind energy, being both environmentally sustainable and renewable, presents challenges to power grid reliability due to the intermittent nature of wind speed and the influence of noise interference. In response, Xueyi Ai propose a two-stage preprocessing strategy alongside an LSTM-based model for short-term wind speed prediction in 2022, according to experiment data, the least MAE MSE RMSE MAPE among, which is namely 0.6681 0.7737 0.8796 0.2298 [12].

In the subsequent stage, a novel approach to wind power forecasting is introduced by Guoqing An in 2021, which integrates the combination of the Sparrow Search Algorithm (SSA) with the Deep Extreme Learning Machine (DELM) model exhibits superior performance in ultra-short-term wind power prognostication, as indicated by experimental results [13]. The coefficient of determination (R²) stands at 0.927, while the RMSE and MAE of ethics are 115.446.and 69.803.

3.4. Comparison of experimental data

The following table 1 shows RMSE, MAE, and MAPE of improved system consisted of reinforced algorithm.

Table 1. Three model accuracy comparing

Upon examination of the provided table, it becomes evident that the Grey Model demonstrate the lowest RMSE at 1.1422%, indicating its superior predictive accuracy. Conversely, the Sparrow Search Algorithm (SSA) demonstrates smaller MAE and MAPE values compared in constriction of other two algorithms, which is 0.687 \( \% \) and 0.2298 \( \% \) respectively. Besides, the comparative analysis of test results reveals that the data pertaining to System A exhibit a relatively diminished degree of volatility, whereas the test outcomes associated with System B demonstrate a markedly elevated level of volatility. This observation suggests that System A displays a greater degree of stability and consistency in its test results compared to System B, which exhibits considerable fluctuations and variability.

4. Conclusion

In pursuit of refining enhancing the precision of wind power forecasting, this essay presents a hybrid prognostic framework predicated on grey wolf optimization, Grey Model (GM) and Sparrow Search Algorithm (SSA). At first, these are these improved models based on GWO, A combined model of the Kernel Extreme Learning Machine (KELM), which integrates Variational Mode Decomposition (VMD) and an Extreme Learning Machine (ELM), is proposed. (KELM) and the model employs CEEMDAN, GWO, and Bi-LSTM for prediction Then, when it comes to grey model, the EMD-based gray amalgamated prognostic model, refined and comprehensive modification to the GM (1,1) model is suggested. Moreover, in the terms of SSA, sine cosine search-sparrow search algorithm, which is called SSSA, A forecasting model utilizing Long Short-Term Memory (LSTM) architecture and combines related to the SSA with DELM. Grey model is suitable for the limited data and effective for predicting data sequences with very few (e.g. Only 4) and low data integrity and reliability. Besides, the Grey Model is known for its simplicity and ease of implementation, requiring minimal parameter tuning.

(2) The benefits of the GWO model encompass efficiency, robustness, simplicity, and versatility, positioning it as a promising optimization technique for addressing complex real-world problems, while it also possesses the drawback like low accurate rate when applying the algorithm to real-world optimization problems.

(3) SSA tends to be relatively simpler compared to GWO, with fewer parameters and a more straightforward algorithmic framework, and less stable as stated by the table.