1. Introduction

The central aim of this paper is to categorise the predominant instruments in musical audio. It opens avenues to distinguish orchestral music, known for its complex arrangements, with a musical impact deemed unique in the sphere of music performance. Orchestral works, like symphonies, can involve about 100 musicians. The instruments used in these compositions typically cover the string, brass, woodwind, and percussion families, with several of these instruments being the focus of this study. This is considered a multi-labelled classification problem [1], compared to other multi-class classifications that simply classify one instrument in musical audio. Wav2Vec 2.0 [2] has proven effective in acquiring speech representations directly from raw audio at 16kHz as shown in Figure 1. This model is applied to discern "instrumental" representations across a range of 11 distinct instruments in this paper. Modifications are made to the model, which involves adjusting the dimensions of the convolutional layers in the feature extraction section and altering the number of hidden layers in the transformer [3] component of the model. The study incorporates data processing techniques like resampling the audio and padding the input into the model. Regarding model evaluation, the paper discusses overall accuracy and accuracy specific to multi-labelled classification. Additionally, it delves into precision, recall, the F1-score, and the utilisation of the confusion matrix for each instrument as crucial metrics for assessing the model's performance.

Figure 1. Musical audio resampled at 16kHz.

2. Literature Review

In the study conducted by Bosch et al. [4], an investigation was carried out focusing on the detection of primary musical instruments within polyphonic audio signals. In this study, a comprehensive assessment was conducted on a spectrum of sound segregation techniques, each varying in complexity, to determine their effect on the precision of instrument identification algorithms. The algorithms evaluated include Support Vector Machines, the Flexible Audio Source Separation Framework, and the Simple Left/Right-Mid/Side (LRMS) Separation method. Additionally, it was established that the inclusion of a sound segregation phase prior to the deployment of the instrument recognition algorithm notably enhances the accuracy of the results, with improvements observed up to 32%. The findings of this study indicate that the efficacy of instrument recognition algorithms is significantly improved when they are trained using features derived from isolated audio streams. As opposed to the approach outlined in their research, this paper leverages a transformer model to solve the classification issue without segmenting instruments.

Gururani et al. [5] addressed the challenge of identifying musical instruments in multi-instrumental compositions with weakly labelled data. They proposed an attention-based framework to enhance classification accuracy under these conditions. This approach addresses the limitations of existing datasets, such as MedleyDB, which offers detailed per-frame annotations but is small in scale, and OpenMIC, which provides basic labels indicating the presence or absence of instruments in music segments but is larger in scale. The study demonstrates that incorporating an attention mechanism enables the model to focus on specific temporal segments relevant to each instrument, significantly improving classification accuracy across all 20 instruments in the OpenMIC dataset compared to conventional models like binary relevance random forests, recurrent neural networks, and fully connected neural networks. The attention model not only outperforms these baselines in classification metrics but also provides interpretative insights by highlighting the audio segments that the model prioritises for instrument recognition. Additionally, the use of an attention mechanism facilitates contextual understanding by selectively emphasising sounds or phonemes essential for comprehending the context, effectively managing long sequences by identifying the most critical parts of the input.

Solanki et al. [6] tackled the challenge of identifying the predominant instrument in real-world polyphonic music, a task that aligns with the focus of this paper. The researchers utilised a Mel spectrogram representation to convert audio data into a matrix form, suitable for processing by a model similar to AlexNet. Their methodology demonstrated remarkable accuracy, achieving a 92.8% success rate in instrument recognition, thus underscoring its potential utility in music information retrieval. However, the study lacks clarity regarding the threshold applied in the Softmax function for label output. Given that the testing set is multi-labelled, varying thresholds could yield different accuracy results. Also, in the context of multi-labelled classification, it remains ambiguous whether the reported accuracy reflects instances where the entire set of predicted labels for a sample precisely matches the corresponding set of true labels.

Mahant et al. [7] conducted research on the automated classification of musical instruments using convolutional neural networks (CNNs) and Mel-frequency cepstral coefficients (MFCCs), employing the Philharmonia dataset that encompasses twenty distinct musical instrument classes. They addressed dataset imbalance by implementing audio data augmentation techniques. Their methodology highlighted the effectiveness of MFCCs in capturing the timbral qualities of musical instruments. The study also discussed the potential of integrating this model into real-time applications due to its compact and efficient structure. Contrasting with their approach, this paper employs raw musical audio as input, which, while more straightforward, introduces greater challenges in resolving the classification problem.

3. Methodology

This section outlines the methodology proposed for the investigation. The objective of this study is to harness the potential of Wav2Vec 2.0, a speech recognition framework adept at deriving speech representations from unprocessed audio.

3.1. Model Development

The Wav2Vec 2.0 model employs a multi-layer convolutional feature encoder that processes raw audio into latent speech representations through temporal convolution, layer normalisation, and GELU [8] activation, with the input normalised to zero mean and unit variance [2]. The output is discretised using a quantisation module that employs product quantisation from multiple codebooks, facilitated by the Gumbel softmax and a straight-through estimator, enabling differentiable codebook entry selection. These discretised representations feed into a transformer-based context network incorporating a convolutional layer for relative positional embedding, superseding fixed embeddings, followed by layer normalisation. The model also uses a masking and contrastive task strategy, masking certain encoder outputs and replacing them with a common feature vector.

The architecture of the Wav2Vec 2.0 is modified by reducing the convolutional layers’ dimensions from 512 to 256, the number of hidden layers from 12 to 4, and attention heads from 12 to 8. Additionally, the model head is modified to include three identical structures, each with a fully connected layer followed by layer normalisation and a dropout layer at a rate of 0.3, preceding the final classifier layer. These changes result in a model comprising 35,445,387 parameters.

3.2. Dataset

The dataset employed in this research is IRMAS [9], specifically designed for training and testing systems intended for the automatic recognition of primary instruments in musical audio. It features a diverse range of instruments, encompassing cello (cel), clarinet (cla), flute (flu), acoustic guitar (gac), electric guitar (gel), organ (org), piano (pia), saxophone (sax), trumpet (tru), violin (vio), and human singing voice (voi). This dataset is an adaptation of the one compiled by Fuhrmann in his doctoral thesis [4]. However, unlike Fuhrmann's approach, in the paper, the testing set is utilised for the phases of training, validation and testing of the model. This deviation is due to the testing set's multiple labels per sample, making it a suitable resource for the proposed methodology of this study. Fuhrmann's testing set is divided in an 8:1:1 ratio, with the specific distribution of this split detailed in Figure 2.

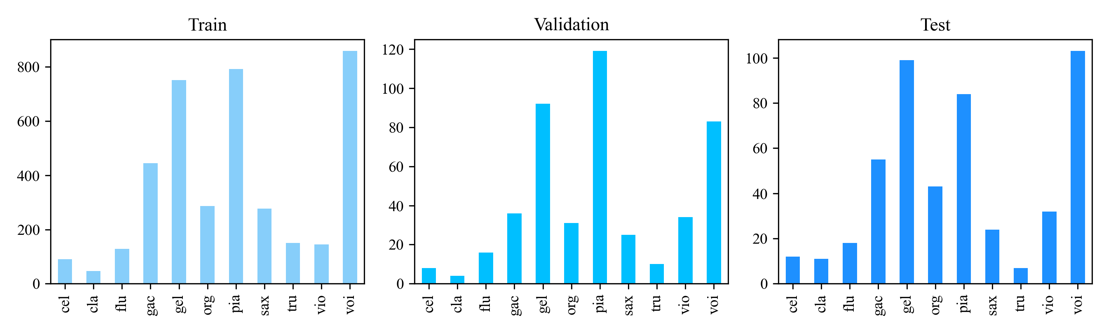
Figure 2. Distribution of the classes in the datasets.

3.3. Data Processing

The process involves critical steps like resampling, padding, and multi-hot encoding. Since Wav2Vec 2.0 requires 16 kHz input, the audio is resampled from 44 kHz using the librosa library [9]. For feature extraction, the Wav2Vec2FeatureExtractor from Hugging Face [10] is utilised. Labels are multi-hot encoded as shown in Table 1, where a "1" denotes the presence of predominant instruments, while "0" indicates their absence, which demonstrates a substantial number of actual negatives in the dataset.

Table 1. Multi-hot encoded labels.

3.4. Loss Function

Given that the task involves multi-labelled classification, Binary Cross-Entropy, is utilised as shown in Equation 1. N represents the total number of observations in the dataset, \( {y_{i}} \) denotes the actual label of the \( i \) -th observation (being either 0 or 1), and \( {p_{i}} \) is the predicted probability of the \( i \) -th observation belonging to class 1. The term \( {y_{i}}\cdot log({p_{i}}) \) contributes to the loss when the actual label \( {y_{i}} \) is 1, with the loss intensifying as the predicted probability \( {p_{i}} \) diverges from 1. Conversely, the term \( (1–{y_{i}})\cdot log(1–{p_{i}}) \) affects the loss when the actual label \( {y_{i}} \) is 0.

3.5. Technical specifications

The experiments were conducted on a system running Ubuntu 20.04 as the operating system. The hardware specifications include a CPU with 10 cores, a GPU with an A100-PCIE-40GB, a memory capacity of 72 GB, and a storage space of 80 GB.

4. Results

The threshold set for predicting the presence of instruments is 0. The evaluation metrics focus on several aspects: training loss and accuracy, accuracy, precision, recall, F1-score, and confusion matrix.

4.1. Training Loss and Accuracy

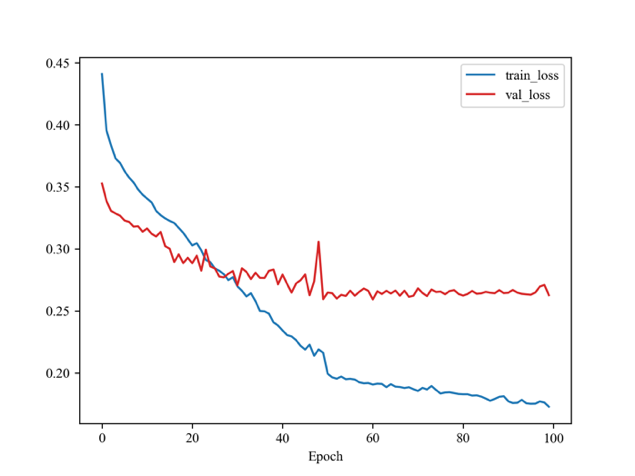
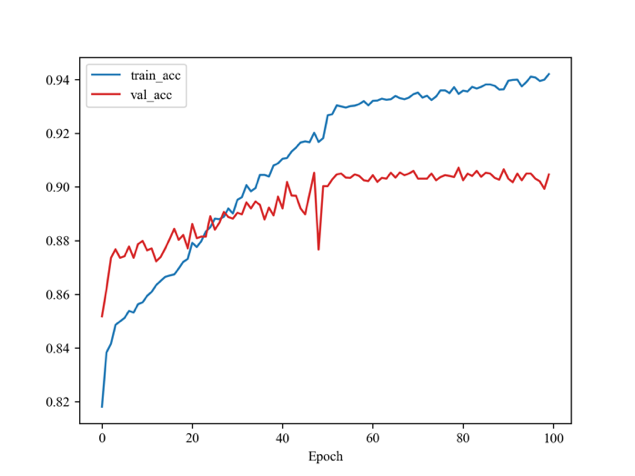
As illustrated in Figure 3, the model’s loss declined rapidly when training, whereas the validation loss decreased slowly and slightly. Figure 4 illustrates a continuous increase in the model's accuracy on the training set. However, the accuracy on the validation set, while initially improving, exhibits an earlier plateau. The model selected is from Epoch 61 where it has the lowest validation loss during training.

4.2. Accuracy, Precision, Recall, and F1-score

Table 2 showcases the accuracy rates for different instruments, ranging from approximately 70% to 96%, indicating variable model performance across instruments. Instruments such as the cello, clarinet, and trumpet exhibit the highest accuracy, while the electric guitar has the lowest within the group. Additionally, in multi-labelled classification problems, accuracy can be measured by a stricter criterion that considers a prediction accurate only if it matches the true labels "exactly". Using this more stringent measure, the model's accuracy is reported at 0.32.

Table 2. Accuracy per instrument.

Table 3 reveals that the model completely fails to identify true positives for the cello and clarinet, as indicated by zero precision and recall scores. This failure may result from inadequate data representation or an inability to distinguish the unique characteristics of these instruments. For the flute, acoustic guitar, and violin, the model shows high precision but varied recall scores, suggesting it accurately identifies these instruments when detected but frequently fails to recognise them. The organ and trumpet display uniformly low performance, highlighting significant recognition challenges. In contrast, the electric guitar, piano, saxophone, and human voice achieve more balanced and moderately high F1-scores, indicating better overall performance.

Table 3. Classification Report.

4.3. Confusion Matrix

In Figure 5 the model's performance for cello and clarinet indicates a significant shortfall, as it fails to correctly identify any of both instruments. All occurrences of cello and clarinet are predicted as negatives, signifying a complete miss in recognising these classes. For instruments like organ and trumpet, the model exhibits a limited ability to identify true positives, coupled with a high count of false negatives. This pattern suggests that the model struggles to detect these instruments when they are present, leading to a low recall. In the case of the piano, acoustic guitar, and electric guitar, there appears to be a more balanced distribution between true positives and false negatives. This suggests a moderate level of accuracy in the model's predictions for these instruments. The higher recall for the instruments indicates a better proficiency of the model in detecting their presence. Across all instruments, there is a consistently high number of true negatives. This implies that the model generally performs well in predicting the absence of an instrument, demonstrating its effectiveness in avoiding false positives.

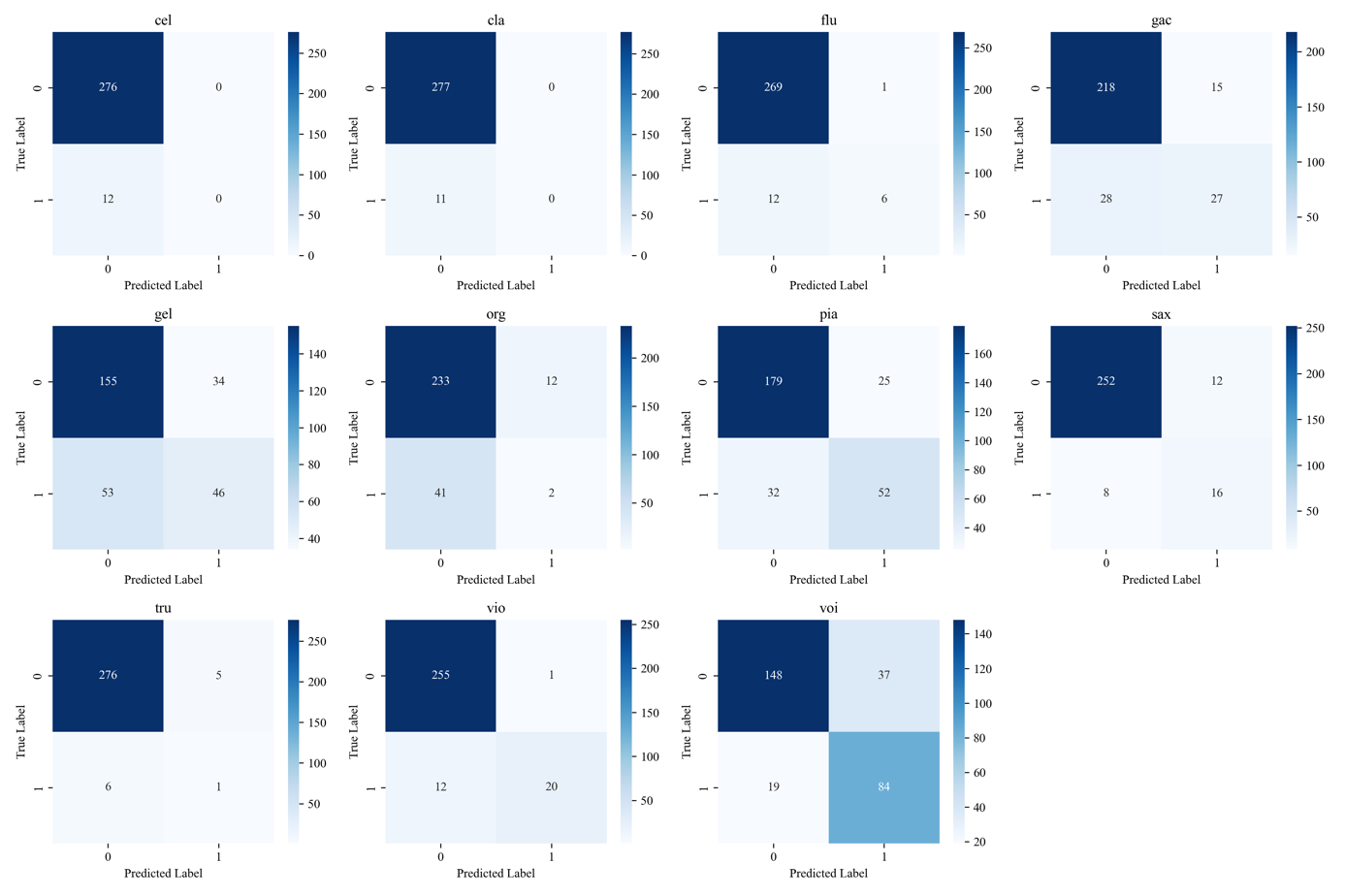
Figure 5. Confusion matrix for each instrument.

5. Discussion

The results indicate that the modified Wav2Vec 2.0 model achieved varying levels of performance across different instruments, and generally performs well in predicting the absence of an instrument. However, as noted in Section 3.2, following the multi-hot encoding of the labels, the dataset exhibits a significant proportion of actual negatives. Consequently, the F1-score, which provides a balanced measure of a model's precision and recall, is more suitable for analysis in this context than considering precision and recall independently. The notably elevated F1-scores associated with the piano, saxophone, violin, and human voice indicate a strong performance, marked by a minimal incidence of misclassifications and a low rate of overlooked true cases, as opposed to cello, clarinet, organ, and trumpet.

The dynamic range and articulation of instruments significantly affect their sonic signature. The piano and saxophone, with their vast dynamic range and the ability to play both staccato and legato, might be easier for the model to identify due to their distinct and variable sound. In contrast, instruments with more subtle articulation changes, like the organ, might pose more challenges.

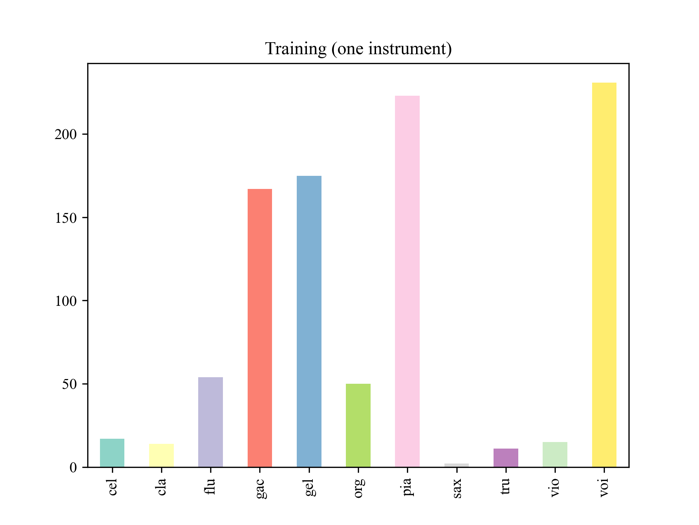
The audibility of an instrument within a musical composition significantly impacts its ability to be recognised. Instruments, such as violins or the human voice, which usually lead the melody at higher volumes, are more readily identifiable due to their dominance in the audio mix. In Figure 6, the relatively sparse number of violins in the training set may cause higher accuracy. Conversely, instruments that are relegated to background roles or serve as harmonic support, like the organ, face detection challenges even though they have a moderate number of training samples, resulting in lower metrics of precision, recall, and F1-score.

6. Conclusion

The results of the study are valuable in enhancing the understanding of transformer models for musical audio analysis and reveal the model's varying effectiveness in identifying different instruments, with notable success in recognising violins, pianos, saxophones, and human voices. These findings underscore the potential of transformer-based models in complex audio recognition tasks. Interestingly, instruments such as the violin and saxophone may not require prior separation for moderate accuracy in training. Despite having the fewest solo samples, the saxophone achieves an accuracy of 0.93 and an F1-score of 0.62. However, the research also identifies areas for further investigation. The model's performance in detecting instruments with a narrower dynamic range and lower volume, such as the organ, or those sparsely represented in the dataset, like the cello and clarinet, needs enhancement by expanding the dataset to improve training and accuracy. Additionally, incorporating timbral and contextual information could refine the model's effectiveness. Exploring the model's adaptability to different audio qualities and formats would increase its application range.