1. Introduction

In today's rapidly developing digital age, online advertising and online learning are becoming more and more common, and the amount of information that users have to receive is exploding. Therefore, decision optimisation is of paramount importance. The problem of information explosion involves various fields, including online advertising, for example, according to E-marketer's data shows that in 2023 the global digital advertising market size of about $837 billion, and in the next few years will continue to maintain the growth trend. In the huge market, enterprises have to face the dynamic data of various online platforms continue to change, in the face of these dynamic and complex data, the multi-armed bandit algorithm can help enterprises to adjust their strategies in real time to achieve the maximum return on investment [1]. In the field of e-commerce, consumers have different preferences and purchase rates for different products, according to the multi-armed bandit algorithm, platforms can accurately push related products and advertisements to improve the purchase rate and satisfaction of users. With the amount of data grows and the computational power continues to improve, the multi-armed bandit algorithm is also constantly improving and perfecting. The combination of the multi-armed bandit algorithm with deep learning, reinforcement learning and other cutting-edge technologies will also have a broader prospect.

The Multi-Armed Bandit (MAB) problem was initially introduced by Robbins in 1952 [2]. MAB is actually a sequential decision model, wherein the objective entails the selection of actions in a stepwise manner to optimize the overall reward acquired over time [3]. It mainly includes the following common algorithms: the greedy algorithm, which always chooses the bandit arm with the highest known expected reward without any exploration process. Currently, there are many strategies to balance the dilemma between exploration and exploitation in the MAB problem, the ε-greedy algorithm, which selects the bandit arm with the highest known expected reward most of the time, but randomly chooses other bandit arms for exploration with a small probability ε [4]. Explore-Then-Commit (ETC), the Upper Confidence Bound (UCB) algorithm, which selects the bandit arm with the highest upper confidence bound, i.e., the current estimated expected reward plus a confidence level, to balance exploration and exploitation; and Thompson sampling (TS), which uses Bayesian methods to update the posterior distribution of the reward for each bandit arm and makes selections based on the posterior distribution. Numerous studies have concentrated on the application of multi-arm bandit algorithms in advertising, exploring different aspects of their usage, such as algorithmic approaches, contextual factors, and personalization potential [5]. Currently, the TS algorithm has surged in popularity, due to its empirical successes and robustness across a wide array of applications [6]. This Bayesian approach to the MAB problem has demonstrated remarkable efficacy in scenarios like large-scale A/B testing and the placement of online advertisements [7].

MAB problem is a fundamental issue in reinforcement learning, which focuses on finding an optimal balance between seeking potential better options and choosing the currently known best option, i.e., between "exploration" and "exploitation". The study of such balancing strategies is crucial for understanding more complex decision-making processes. In reality, there is an inherent contradiction between "exploration" and "exploitation". If only "exploration" is conducted, although it can provide a good estimation of the reward for each item, it consumes a large number of recommendation opportunities, making it impossible to obtain the current optimal recommendation within a limited number of recommendations [1]. Conversely, if only "exploitation" is conducted, it becomes difficult to accurately estimate the expected reward of items, leading to the risk of being trapped in local optimality and failing to identify the item that users are most interested in among all options [1]. Therefore, despite the significant progress made in multi-armed bandit algorithms, there is still considerable potential for exploring their complexity and broader applications.

This article aims to gain a deeper understanding of the MAB algorithm by analyzing several of its variants, and to provide guidance for the future development and wide application of the multi-armed bandit algorithm in various fields.

2. Methodology

2.1. Data sources and clarifications

The experimental part of this article involves an internationally published datasets, MovieLens, which is widely recognized and has been repeatedly applied in the study of multi-armed bandit algorithms. This dataset contains ratings and tags settings for the movie recommendation service MovieLens, which includes five levels of ratings. It includes over 100000 ratings and over 3000 tags for over 9000 movies. These data were created by 610 randomly selected users, and all selected users rated over 20 movies. It does not contain any demographic information. Each user is represented by an id, and no other information is provided. This experiment preprocessed the dataset and only extracted the relevant information required for the experiment.

2.2. Indicator selection

The MovieLens dataset contains some irrelevant data. Therefore, this experiment involves analyzing and preprocessing the dataset to extract the necessary portion for the study. In this experiment, movie genres are selected as the arms, and the user ratings for these genres serve as the rewards for users choosing a particular genre. The performance of various algorithms is analyzed by comparing the average cumulative regret generated by three algorithms under different iteration counts.

2.3. Method introduction

In this paper, three algorithms are employed, namely, ETC, UCB, and TS. The following is an explanation of the three methods.

The ETC algorithm is a straightforward yet efficacious approach to the MAB problem introduced by Perchet et al. in 2015 and then further researched by Garivier et al. in 2016 [8, 9]. The ETC algorithm can be understood as a two-phase strategy, comprising the Exploration Phase and the Commitment Phase. During the Exploration Phase, the algorithm attempts each bandit a certain number of times to gather information about their reward probabilities. The goal of this phase is to understand the performance of each bandit in order to make better choices in subsequent phases. Following the Exploration Phase, the Commitment Phase begins, where the algorithm selects the seemingly best bandit based on the collected data and sticks to it for all subsequent steps. The objective of this phase is to maximize long-term rewards by consistently exploiting the known best bandit. The ETC algorithm is straightforward in its approach, making it easy to understand and implement (Figure 1).

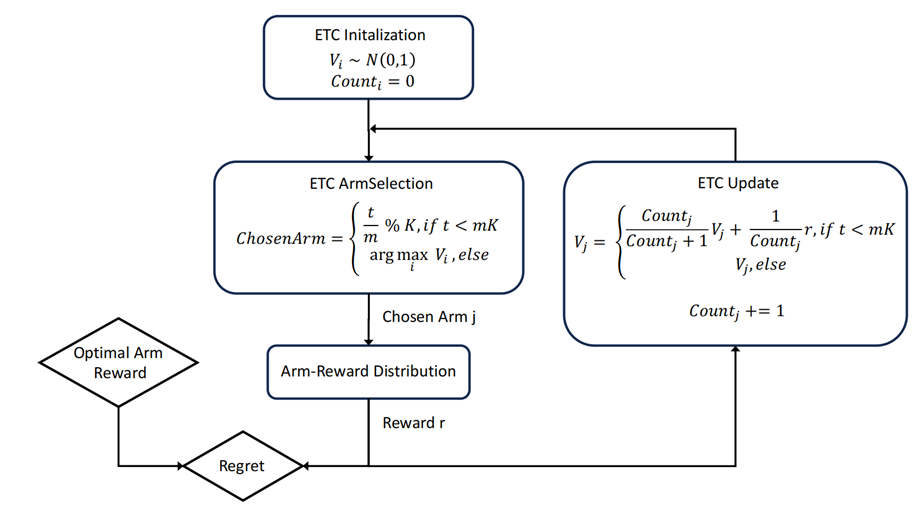
Figure 1. The process of the ETC

The UCB algorithm concluded by Cesa-Bianchi et al. [10]. The fundamental idea of the UCB algorithm is to select the optimal option by calculating the upper confidence bound for each option. Specifically, the UCB algorithm takes into account not only the average reward of each option but also the uncertainty regarding its true reward. This uncertainty is measured by the width of the confidence interval. The wider the confidence interval, the less people know about the option, thus necessitating more exploration (Figure 2).

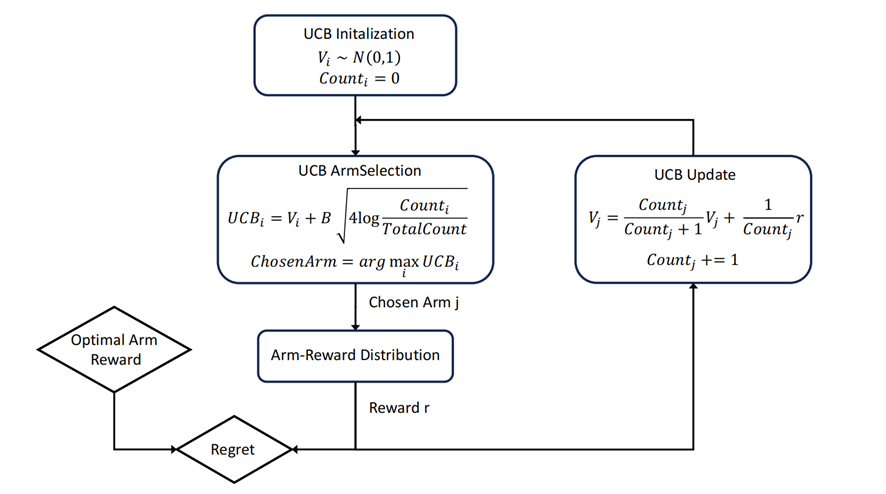
Figure 2. The process of the UCB

Thompson Sampling is a probabilistic algorithm for the MAB problem, as detailed extensively by Agrawal and Goyal [11]. The TS method in the MAB algorithm assumes that the probability of each arm yielding a reward follows a specific probability distribution, typically the Beta Distribution. The Beta Distribution is governed by two shape parameters, a and b, which represent the number of rewards and no rewards, respectively. After each arm is selected and attempted, the a and b values of that arm are updated based on the outcome, thereby updating the underlying Beta Distribution (Figure 3).

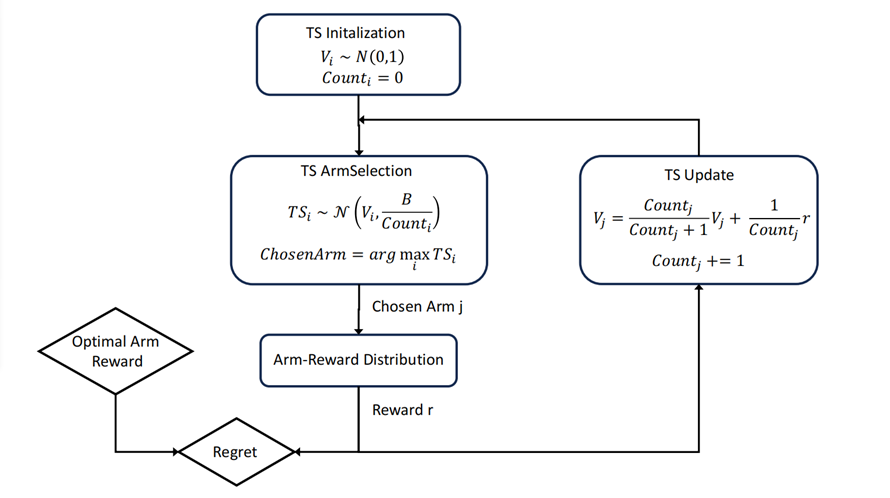
Figure 3. The process of the TS

3. Results and discussion

3.1. The performance of various algorithms

In this experiment, three algorithms (ETC, UCB and TS) were applied to the processed MovieLens datasets under the Python environment. Figure 4 shows the average regret of three methods at time steps of 5,000, 10,000, and 20,000. The x-axis indicates the number of iterations, while the y-axis indicates the average cumulative regret. The error bars indicate one standard deviation above and below the mean, providing a measure of the variability in the results. Figure 5 demonstrates the variance of the three methods when performing 10 experiments with an iteration count of 20,000. Figure 6 shows the cumulative regret of the three methods when setting different hyperparameters.

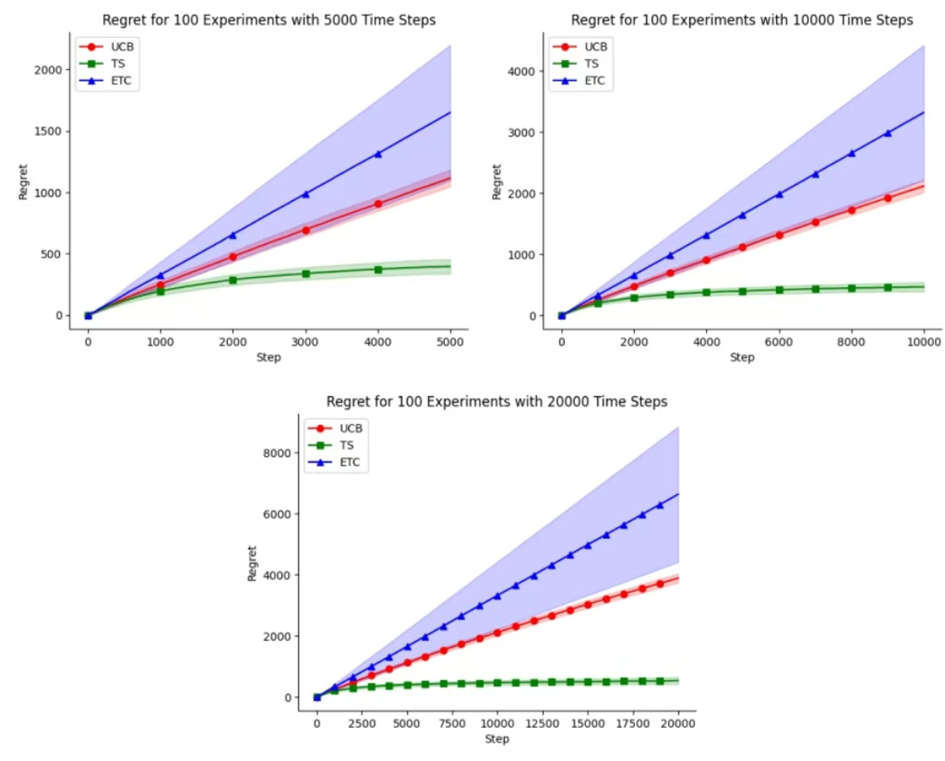
Figure 4. Average Regret of ETC, UCB, TS for 100 Experiments with different Time Steps

Figure 4 shows the cumulative regret of three algorithms at different iteration times in 100 experiments. It can be seen that the cumulative regret of the TS algorithm is significantly lower than the other two algorithms. And its accumulated regret is less affected by the number of iterations compared to the other two algorithms.

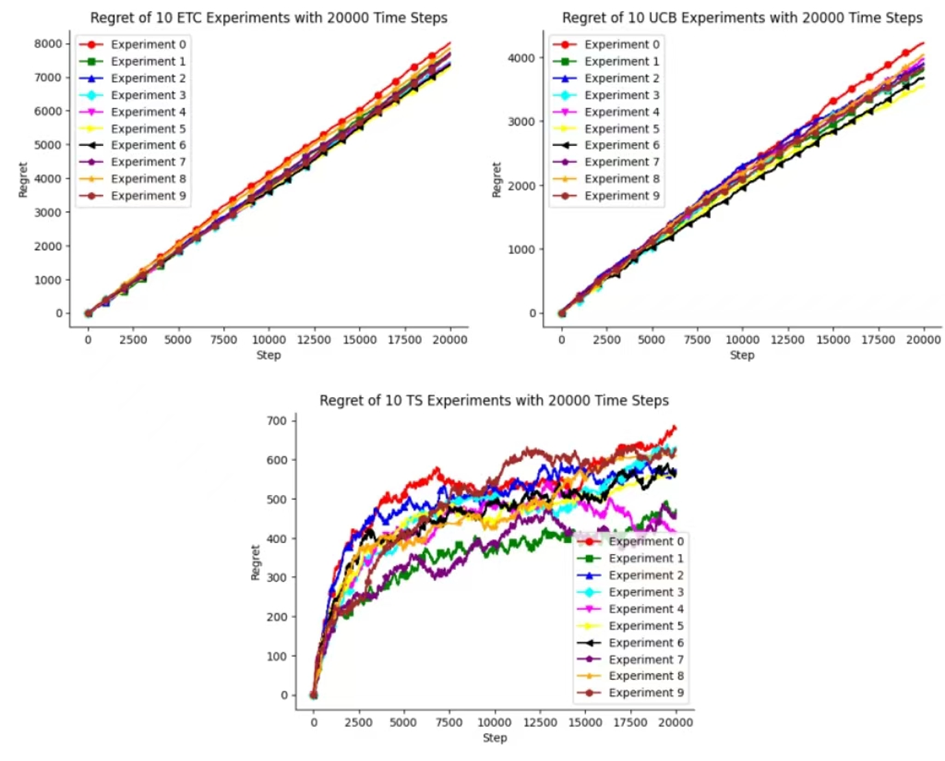
Figure 5. Cumulative Regret of ETC, UCB, TS for 10 Experiments with 20,000 Time Steps

This figure 5 shows the cumulative regret of three methods after 10 experiments with the same number of iterations. Comparing the cumulative regret of three methods, it was found that the TS algorithm has the smallest variance in cumulative regret. So in this experiment, it is obvious that the TS algorithm has more advantages.

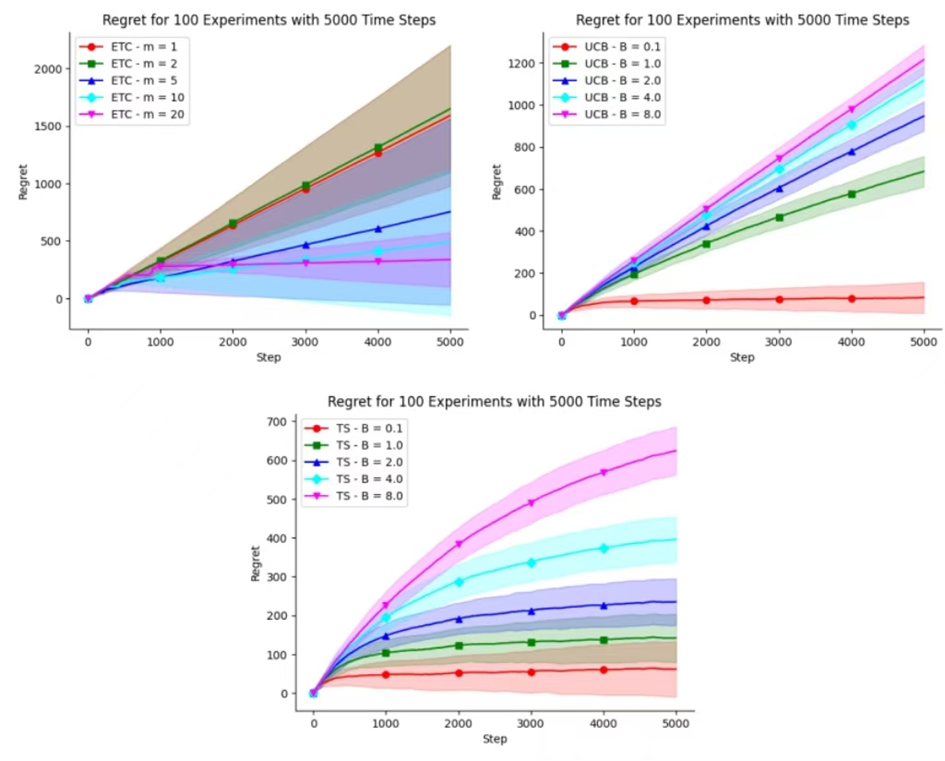
Figure 6. Average Regret of ETC, UCB and TS with different hyperparameters for 5,000 Time Steps

The above figure 6 describes the cumulative regret of three methods when setting different hyperparameters. Setting different hyperparameters during experiments can have an impact on accumulated regret. So for specific research and experiments, appropriate hyperparameters should be adjusted to achieve better experimental results.

3.2. Discussion

Based on Figure 4, as the number of time steps increases, the cumulative regret of the TS algorithm is significantly smaller than that of the other two methods, while the cumulative regret of the ETC algorithm is the largest. Referring to Figure 5, when comparing the variances of the three methods during a small number of experiments, the ETC algorithm exhibits the largest variance. Furthermore, as the number of time steps increases, the variance of the cumulative regret becomes even larger for the ETC algorithm. At this point, the TS algorithm is considered to be the optimal algorithm.

Figure 6 shows that when the hyperparameter m in the ETC algorithm is set to 20, it achieves the lowest cumulative regret. Additionally, as m increases from 1 to 20, the cumulative regret decreases. For the UCB algorithm, when the hyperparameter B is set to 0.1, it achieves the lowest cumulative regret. Furthermore, as B increases from 0.1 to 8.0, the cumulative regret exhibits an upward trend. Similarly, for the TS algorithm, when the hyperparameter B is set to 0.1, it achieves the lowest cumulative regret. And as B increases from 0.1 to 8.0, the cumulative regret also shows an upward trend.

4. Conclusion

This experiment explores and analyzes the different performances of three commonly used MAB algorithms (ETC, UCB, and TS) on the MovieLens dataset. This experiment uses Python to draw charts to represent the cumulative regret of each algorithm. By comparing the images of three algorithms at different iteration times, it was found that as the time step increased, the ETC method had the highest cumulative regret, while the TS method had significantly lower cumulative regret than the other two methods. In addition, it was found that the cumulative regret variance of the TS method was the smallest among the three methods when conducting a limited number of experiments. Ultimately, the TS method demonstrates more stable and superior performance. Additionally, adjusting different hyperparameters has an impact on the cumulative regret of all three methods. So setting reasonable hyperparameters can play a significant role in improving the performance of algorithms.

Another point worth mentioning is that this experiment only studies the processing of MovieLens dataset by three algorithms. However, each MAB algorithm has its unique advantages and disadvantages, and the choice of algorithm depends on specific problems and goals. Further research on the application of MAB algorithms is still needed.

Authors contribution

All the authors contributed equally and their names were listed in alphabetical order.