1. Introduction

Behavior trees (BTs) were originally used by game developers to simplify and structure the behavior design of non-player characters (NPCs) [1]. They originated from the need to overcome the rigidity and maintenance difficulties encountered by finite state machines (FSMs) when dealing with complex and dynamic behaviors. Behavior trees use a hierarchical tree structure with nodes representing behaviors or decision points, through which behaviors can be modularized, reused, and intuitively designed. At the heart of a behavior tree is the root node, which serves as the starting point for the NPC’s decision-making. From this root, the tree branches out into various composite nodes, each dictating the flow of execution through their children. Composite nodes, such as sequences and selectors, determine how the NPC processes a series of actions or decisions. A sequence node, for example, executes its children in order until one fails, while a selector node does the opposite, continuing until one succeeds. Parallel nodes, another type of composite node, execute multiple children simultaneously and can determine success or failure based on custom conditions.

Complementing these are decorator nodes, which have a single child and modify its behavior by adding conditional checks or repeating actions. Examples include inverters, which reverse the success or failure status of their child, and repeaters, which repeat the child’s action until a condition is met. At the leaf nodes of the tree, the actual actions and conditions are defined. Action nodes perform specific tasks, such as moving to a location or attacking an enemy, while condition nodes check specific criteria, like whether the NPC’s health is below a certain threshold. This hierarchical and modular structure allows developers to create and manage sophisticated NPC behaviors efficiently, enabling easy adjustments and expansions without significant changes to the overall architecture. In complex virtual environments, especially multi-agent system (MAS) [2], the coordination of non-player characters (NPCs) is a key challenge. Multiple NPCs need to perform various tasks in parallel, and these tasks may depend on or conflict with each other. Therefore, how to effectively coordinate the behavior of these NPCs to achieve consistent and goal-oriented behavior is an important research area.

This paper focuses on advancing the application of BTs within MAS by reviewing and evaluating three distinct algorithmic solutions to this coordination problem. The goal is to not only improve the understanding of effective NPC behavior management but also to contribute systematic approaches that can aid future developers and researchers in the field. Through these evaluations, this study aims to highlight significant conclusions about the efficacy of these algorithms and discuss their broader implications for both theory and practice in game development and robotic simulations. This work hopes to provide foundational insights that can drive further innovation in the deployment and optimization of behavior trees across various interactive and autonomous systems.

2. Background

There are three approaches to addressing the problem of multi-agent coordination using behavior trees.

2.1. Optimization of Behavior Tree

First, it can be solved by improving the behavior tree itself or improving the communication between behavior trees. For example, event-driven behavior tree introduces a new mechanism for better cooperation among multiple agents. The new mechanism is that the behavior trees receive and send request messages to each other. The use of Emotional Behavior Trees (EBT) allows human emotions to be represented on NPCS by introducing new selectors into the behavior tree. The emotional behavior tree is added to the event-driven behavior tree, and the cooperation between agents is realized by sharing synchronous emotional states when NPCS send requests to other NPCS.

2.2. Behavior Tree Search Algorithms

The second direction is to optimize the behavior tree search algorithm. Optimizing the tree search method enhances the efficiency of multi-agent coordination by streamlining the intention-sharing process among agents. This improvement is not merely about the speed of individual tree searches but about how effectively agents can share and update their intentions. Decentralized sub-goal tree search (Dec-SGTS) [3] for multi-agent system is a decentralized search method that can distribute search tasks among multiple NPCs, reducing communication costs through enhanced modularity and semantics.

2.3. Behavior Tree Communication Algorithm

Meanwhile, the problem can be solved by using local communication methods. The latest algorithms all use indirect communication, because traditional direct communication may cause communication interruptions in large group clusters, and knowledge transfer methods that rely on direct communication may encounter communication limitations. There is an IKT- BT [4] method that allows NPCs to coordinate the behavior of multiple NPCs through indirect knowledge transfer through behavior trees. For example, the behavior of an NPC can trigger an event, and the behavior trees of other NPCs can obtain knowledge of the event through query-response to make appropriate behavior adjustments. This method enhances the collaboration between behavior trees.

3. Optimization Of Behavior Tree

With the increasing complexity in the design of game NPCs, behavior tree faces challenges in scalability and management. In recent years, many papers have been published on strategies for optimizing behavior trees themselves [1]. In this paper, two optimization strategies emotional behavior tree and event- driven behavior tree are discussed.

3.1. Emotional Behavior Tree

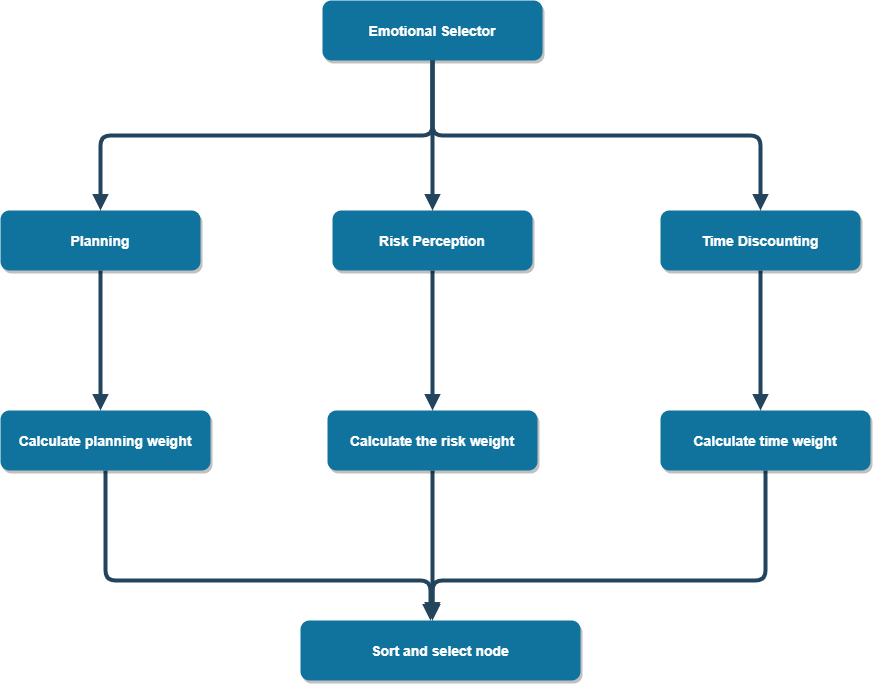
Figure 1. The working mechanism of emotion selector in emotion action tree.

In real life, emotions have a crucial impact on people’s decision-making. Johansson and Dell’Acqua proposed to improve the realism and interactivity of NPCS by introducing an emotion selector into the behavior tree to incorporate emotional factors into the decision-making process of the behavior tree [5].

1) Principle of implementation: Emotion selector is the most core component of emotion behavior tree implementation. It dynamically adjusts the priorities of child nodes and simulates the impact of emotion on decision making according to the current emotional state. The emotion selector combines three main decision influencing factors: planning, risk perception and time discounting, as illustrated in Figure 1.

• Planning: Planning involves the cognitive resources in- vested by NPC in the decision-making process. Different emotional states will affect the planning ability of NPC and have different behavioral tendencies according to different states.

\( {E_{plan}}=\frac{\sum _{i=1}^{Q}p_{i}^{+}}{Q}-\frac{\sum _{j=1}^{R}p_{j}^{-}}{R} \) (1)

Eplan is used to calculate the effect of sentiment on planning effort. Pi+is the influence value of the i-th positive emotion. Pj−is the influence value of the j-th negative emotion. Q is the total number of positive emotions. R is the total number of negative emotions. i is the index of positive emotions, ranging from 1 to Q. j is the index of negative emotions, ranging from 1 to R.

\( {W_{plan,i}}=(1-\frac{1}{1+ω·{plan_{i}}}) \)

\( ·max((1-∅+∅·{E_{plan}}),0) \) (2)

This formula is used to calculate the weight of planning, ω is used to adjust the amount of planning, and ϕ is used to adjust the impact of emotion on planning. plani is the inherent planning value of the i-th child node.

• Risk perception: Risk perception is the NPC’s assessment of action risk. Emotions have a significant impact on how risky an activity is judged to be. Depending on the emotional state, the NPC will choose different risk levels. Positive emotions will make NPCS choose riskier behaviors, and vice versa.

\( {E_{risk}}=\frac{\sum _{i=1}^{M}r_{i}^{+}}{M}-\frac{\sum _{j=1}^{N}r_{j}^{-}}{N} \) (3)

Erisk is used to calculate the effect of sentiment on risk perception. r is the influence value of the i-th positive emotion. M is the total number of positive emotions. N is the total number of negative emotions. i is the index of positive emotions, ranging from 1 to M. j is the index of negative emotions, ranging from 1 to N.

\( {W_{risk,i}}=(1-{E_{risk}}∙δ)·{risk_{i}} \) (4)

This formula is used to calculate the weight of risk perception. δ is used to adjust the effect of sentiment on risk perception. riski is the inherent risk value of the i-th child node. Time discounting: Time discounting refers to the tendency of NPCS to choose immediate but smaller rewards while ignoring delayed but larger rewards when making decisions.

\( {E_{time}}=\frac{\sum _{i=1}^{O}t_{i}^{+}}{O}-\frac{\sum _{j=1}^{P}t_{j}^{-}}{P} \) (5)

Etime is used to calculate the effect of sentiment on time discounting. t is the influence value of the i-th positive emotion. O is the total number of positive emotions. P is the total number of negative emotions. i is the index of positive emotions, ranging from 1 to O. j is the index of negative emotions, ranging from 1 to P.

\( {W_{time,i}}=(1-\frac{1}{1+μ·time}) \)

\( ·max((1-λ+λ·{E_{time}}),0) \) (6)

This formula is used to calculate the weight of time dis-counting. µ is used to adjust the time span and λ is used to adjust the emotional influence. time is the emotional effect delay time Finally, the three calculated weights are added as the total weight, and the child nodes are sorted according to the weight, and the node to be executed is selected according to the probability distribution. These emotions include both positive and negative emotions, such as happiness, fear, anger, sadness, etc. These emotions influence the decision-making process of the NPC by adjusting the weights of the three aspects mentioned above. Moreover, each NPC has a different emotion, and combining this emotion selector with the event-driven behavior tree described below can lead to better coordination between multi-agents.

3.2. Event-driven Behavior Tree

Event-driven behavior tree is another strategy to optimize the behavior tree itself. Event-driven behavior trees (EDBTs) are the result of the various implementations of BTs that have developed over time to meet industry demands and continue to improve in efficiency and capabilities. An event-driven behavior tree addresses these performance problems of behavior trees when managing large-scale and complex behaviors. It solves these problems by introducing new types of nodes as well as changing the way processing is performed inside the tree [6].

1) Mechanisms for event-driven behavior trees: Three new Node types are introduced in EDBT: Request Handler Node, Soft Request Sender Node and Hard Request Sender Node.

Request Handler Node (RH): Receives and processes re-quests from other NPCS.

Soft Request Sender (SRS): It is used to send requests that do not require an acknowledgment (such as notification requests and simple collaborative tasks).

Hard Request Sender (HRS): It is used to send requests that need to be acknowledged and is suitable for critical tasks and complex tasks that require multiple agents to cooperate.

Figure 2. EDBT work flow chart.

Figure 2 shows the work flow of EDBT. Each RH nodes continuously listen and receive requests from other agents, and the received requests are stored in their own mailbox for further processing. When processing is needed, the master selector decides whether to abort the current behavior and pull the request execution from the mailbox based on the current priority and behavior state. The master selector dynamically evaluates the urgency and priority of each request to decide whether to interrupt the current task to handle a new request.

The SRS node sends those requests that do not need to be acknowledged to the target NPC’s mailbox to ensure that the NPC can quickly respond to the event and improve the response speed of the system. SRS requests do not need to wait for confirmations and processing results, thus reducing communication overhead and latency and enabling faster responses than HRS nodes.

HRS nodes send requests that require confirmation and wait for the target NPC to confirm and process the results. HRS nodes coordinate multiple NPCS to perform complex tasks and ensure that critical tasks can be handled efficiently.

2) Methodology for Structuring Agent’s EDBT with Coordination Nodes: The NPC receiving the Request needs to check the mailbox through the Request Handler (RH) node in its behavior tree (BT). When the NPC receives a message, the top-level design of the behavior tree contains a Service Node that periodically calls the checkMailbox method, which drops expired messages and selects available ones. Based on the current priority and behavior status, the RH node decides whether to interrupt the current behavior and processes the new request extracted from the mailbox. By default, this method is disabled when performing important tasks, but it can also be manually enabled and disabled.

Figure 3 describes the EDBT structure for agents using co-ordination node. To satisfy the request processing of the agent, the behavior of the individual is separated, and the order of different types of requests is prioritized. It adopts a structure where the master selector acts as the parent node of both the RH node and the individual behavior node. In addition, the priority order in the graph also ensures that non-critical nodes in individual behavior can be aborted by any request, and non-critical nodes in RH nodes can be aborted by higher priority requests. The Disable CheckMailbox and Enable CheckMailbox task nodes are used to ensure that critical subtrees are not interrupted.

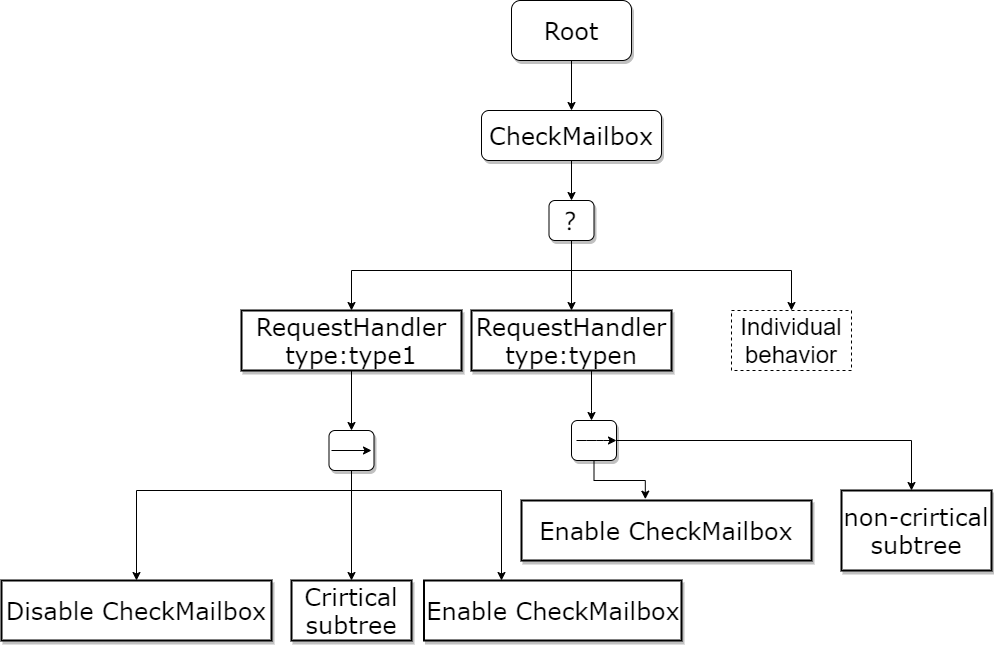
Figure 3. EDBT structure for agents using coordination nodes.

4. Behavior Tree Search Algorithm

4.1. Decentralized Multi-agent Markov Decision Process

1) Markov Decision Process: In a multi-agent system (MAS), the agents’ actions might cause changes in the environment [7]. Every change should be considered by all agents when making their next action decisions. Once developers have created behavior trees with a protocol that controls communication issues for NPCs, the next step is how to figure out an action sequence that fits the current situation and has an impact on the next step. The situation resembles a Markov decision process (MDP). The NPCs use behavior trees to ensure their actions stay within a specific range. After that the task is to compute the probability distribution of their next actions.

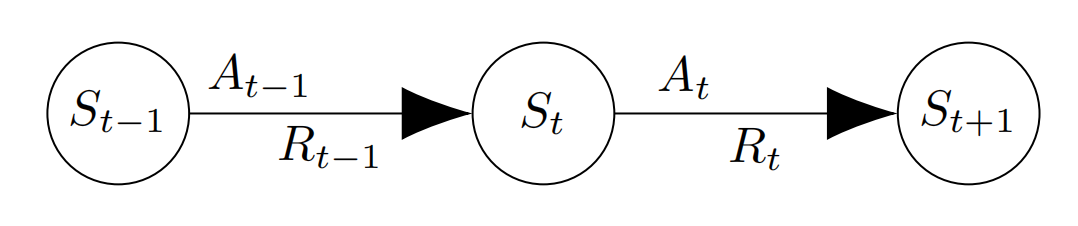
Figure 4. Markov Decision Process.

Figure 4 shows a static Markov decision process, where \( S \) is state, \( A \) is action, and \( R \) is reward. All these variables, \( S \) , \( A \) and \( R \) , are random variables drawn from finite sets. The subscripts of these random variables indicate their corresponding time points, with \( t-1 \) , \( t \) and \( t+1 \) representing the chronological order of events.

\( p \) :

\( p({s^{ \prime }},r|s,a)≜ \) (7)

\( P\lbrace {S_{t+1}}={s^{ \prime }},{R_{t+1}}=r|{S_{t}}=s,{A_{t}}=a\rbrace \)

where \( p \) is state transition probability function. \( p \) is prob-ability. This function refers to calculating the probability of achieving a specific state value \( s \prime \) and \( a \) specific reward value \( r \) at the next time step \( t+1 \) , given the current state \( s \) and the reward \( a \) obtained in the current state. This implies that there is no absolute mapping relationship between these random variables, but rather a certain probability distribution exists.

•Selection Policy In the state transition probability function, it shows the dynamic characteristics of state transitions. However, the task of computing the probability distribution of their next actions has not been solved. Thus, this work turns to the selection policy, which can be used to determine the probability of the next possible actions.

\( π(a|s)≜P\lbrace {A_{t}}=a|{S_{t}}=s\rbrace \) (8)

where \( π \) is selection policy. This function defines the mapping relationship between \( S \) and \( A \) . The function represents the probability of obtaining a specific reward \( a \) at time \( t \) given a particular state value \( s \) at time \( t \) . The term “selection policy” \( π \) refers to the probability distribution between the two random variables \( S \) and \( A \) .

•Value Function Since the functions have demonstrated the probability distribution of actions, finding the best action sequence transforms into another problem: optimizing the functions, which is also referred to as the optimal value function.

\( {G_{t}}={R_{t+1}}+γ{R_{t+2}}+{γ^{2}}{R_{t+3}}+…+{γ^{n}}{R_{T}} \) (9)

where \( {G_{t}} \) is the reward from time t to the end of the game (time T). \( γ(γ∈(0, 1)) \) is discounted factor which is to discount the past. n represents the number of ticks between the current time point and the end of the game, minus one ( \( γ \) ’s exponent starts from 0). For example, the distance between \( t \) and \( t+1 \) is one tick. When the time point of \( R \) is further away from the current time point, its impact on evaluating the value at the current time point decreases. This approach helps to reduce the influence of highly uncertain distant future events on value judgment. In the reward function, only one action sequence is considered. However, all possible sequences should be considered, even if they have different probabilities.

\( {V_{π}}(s)={E_{π}}[{G_{t}}|{S_{t}}=s] \) (10)

where \( {V_{π}}(s) \) is value function using \( π \) selection policy. The function evaluates the quality of the policy. This function indicates that given the probability distribution π between the random variables \( S \) and \( A \) , the true value for a state \( s \) is the expected value of \( {G_{t}} \) under the condition that the state takes the specific values. By comparing the \( {V_{π}} \) values corresponding to different policies \( π \) , the best policy can be selected.

\( {q_{π}}(s,a)={E_{π}}[{G_{t}}|{S_{t}}=s,{A_{t}}=a] \) (11)

where \( {q_{π}}(s,a) \) is the value function, but \( π \) will not determine every mapping relation because \( s \) and \( a \) are used as independent variables. The function evaluates the quality of an action sequence. Based on \( {V_{π}} \) , \( {q_{π}} \) adds the value of the random variable \( A \) to the conditional probability in the expectation calculation, thereby removing the influence of \( π \) . Consequently, it can be used to evaluate the quality of specific values ( \( s \) and \( a \) ) taken by \( S \) and \( A \) . By comparing the \( {q_{π}} \) values corresponding to different values of \( A \) , the best action sequence can be selected.

2) Multi-agent Markov Decision Process: For a single agent, its optimal value function is based on its own objectives. However, in a multi-agent system (MAS), the agents need to work together to achieve a collective goal rather than individual, smaller targets. Thus, the MDP needs to be extended to a multi-agent Markov decision process (MMDP). In addition to defining P (the probability distribution matrix between \( S \) and \( A \) based on \( p \) ), \( π \) , \( {V_{π}} \) and \( {q_{π}} \) for agents, MMDPs also need to introduce the metric of approximate transition dependence to assess the level of collaboration among agents. Specifically, this involves quantifying the impact on an agent’s \( P \) under the condition of actions taken by other agents, and ensuring that this impact remains within a certain range.

\( Δ=P-P \prime \) (12)

where \( ∆ \) is approximate transition dependence. The function represents the difference between the probability distribution of \( S \) and \( A \) without being influenced by the actions of other agents \( P \) and the probability distribution influenced by other agents \( P \prime \) .

3) Decentralized Partially Observable Markov Decision Processes: In an MDP, quantifying the final goal can be addressed through coordination strategies. Most coordination strategies are centralized, using algorithms that employ a global utility function to quantify the system’s collective goal. Using a global utility function to control all the agents in the system is akin to establishing a central control hub from which all decisions are made. If the center makes a mistake, all the agents are affected, leading to a lack of robustness.

If the agents compute their routes independently in a de-centralized manner, the system could become more robust and resilient to individual errors. For example, decentralized partially observable Markov decision processes (Dec-POMDPs), this approach allows for greater flexibility and adaptability, as each agent can respond to changes in the environment without relying on a central control hub. The absence of a central hub is due to coordination between agents being achieved through information exchange methods. In this process, each time an agent decides, it needs to reference information obtained from other agents (which could be observations or actions they have chosen), to avoid decision conflicts and achieve cooperation.

Even if some agents experience interruptions, the others remain unaffected. In the decentralized method, agents still need to communicate their intentions as part of the environmental changes to influence other agents’ decision-making processes.

4.2. Monte Carlo Tree Search

1) Upper Confidence Trees: Initially, when the agent begins the decision-making task, it may be uncertain whether its decision is optimal. This is because each character in the game can only determine if a particular action was the best choice after the game is over and the entire process is reviewed. Thus, the NPCs need to balance exploration and exploitation, trying bold new actions while also leveraging their past experiences. Upper confidence trees (UCT) are one of the methods used to balance boldness and caution in decision-making.

\( UCT(j)={ω_{j}}+\sqrt[]{\frac{2ln{{n_{i}}}}{{n_{j}}}} \) (13)

where \( {ω_{j}} \) represents the average reward of the state presented by node \( j \) . The variable \( {n_{x}} \) represents the number of times node \( x \) has been visited, where \( x \) can be either \( i \) or \( j \) . This function is used to evaluate the goodness of choosing node \( j \) . Both \( i \) and \( j \) nodes represent states. \( i \) node is the parent node of \( j \) node. Since choosing node \( j \) may not lead to the end of the game, there are multiple possible paths to terminal states after choosing \( j \) . Each path has a corresponding sum of rewards, and \( {ω_{j}} \) represents the average of these total rewards. Because nodes \( i \) and \( j \) may have been visited before choosing \( j \) , incorporating visit counts affects the UCT value, helping the agent learn from previously explored paths.

2) Process of Monte Carlo tree search: Monte Carlo Tree Search (MCTS) [8] is widely used in decision-making and game playing scenarios due to its ability to handle uncertainty and explore large decision spaces efficiently.

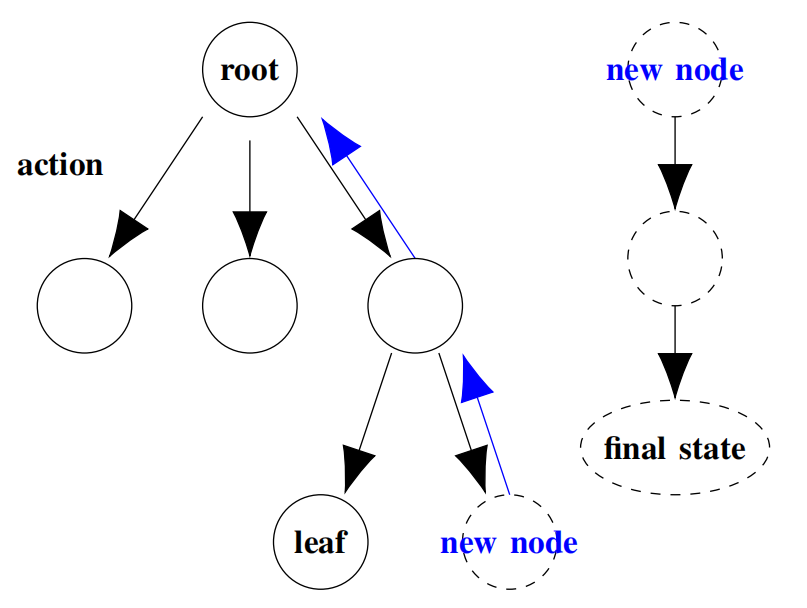
Figure 5. Monte Carlo Tree Search.

Figure 5 shows the process of Monte Carlo tree search, where each node represents a state. Each edge represents an action. The root node represents the initial state, leaf node represents a terminal node (final state) or an unexplored node. The dashed new node on the right of leaf node represents node expanded after UCT selection. A series of dashed nodes connected by action edges on the right represent the process of simulating to a final state using a certain selection strategy. Blue edges denote the backpropagation process.

• Selection Returning to the tree traversal step, starting from the root node, the agent can eventually reach the leaf node by exploring all branches using the UCT algorithm.

• Expansion After reaching the leaf node, if the game is not over, the agent needs to expand the previous node by adding several nodes that represent the next possible states.

• Rollout The agent needs to simulate from the new node to the final state (when the game is over) using a simple random strategy.

• Backpropagation The rollout stage provides a result that can be used to update the nodes along the way back to the root node. This is a change in the weighting of the choice for this pathway.

The overall process begins with traversing from the initial state node (root) to its child nodes, using UCT to select the next promising node until reaching a leaf node. Subsequently, starting from the parent node of the leaf node, a subtree is expanded by adding a new node. The determination of this new node depends on the outcome of simulations, typically involving random selection of subsequent nodes until a final state node is reached, and calculating the sum of rewards along this path. Once the new node is chosen, the process backpropagates from this new node along the path chosen by the selection strategy, updating the visitation counts of all nodes along this path up to the root node.

4.3. Dec-MCTS

Combining the decentralized method (Dec-PoMDP) with Monte Carlo tree search (MCTS) is commonly referred to as Dec-MCTS [9, 10], short for Decentralized Monte Carlo tree search. This algorithm expands MCTS to the multi-agent context by decentralizing the MCTS process, allowing each agent to independently perform its own MCTS search. There are three phases included in the algorithm: local tree search, local intention update, and global intention sharing. In this process, each agent first uses MCTS and references the information received from other agents to generate their own search tree. Then, they update the probability distribution of possible next actions and communicate the updated probability distribution to the other agents. Agents do not make decisions synchronously, so the shared information will only affect agents making decisions subsequently.

4.4. Dec-SGTS

Following Dec-MCTS, each agent will not directly optimize the global utility function but will instead use its local utility function to expand the tree. Decentralized sub-goal tree search (Dec-SGTS) [6] additional contribution usage is rebuilding the tree based on a subgoal-based protocol, abstracting intentions into the probability distribution of subgoal sequences. In higher-dimensional tree search algorithms, this means combining more fundamental, unit-level intentions. For example, in a grid world map abstraction, the basic intentions would be to move one cell in the surrounding grid. However, a subgoal might be to reach an intersection.

1) Subgoal-based Protocol:

• Subgoal Predicate Establish a rule to determine whether a state is a subgoal state [11]. Distinguish between subgoal states that are terminal-related and those that are solely for accelerating the process of reaching the final state.

• Connecting Subgoals The agents need to decide which neighboring subgoal state is the best choice. They use the discounted upper confidence trees (Dec-UCT) algorithm to build a state transition system [12].

• Subgoal-pair Evaluation Evaluating the cost between different subgoal pairs. This evaluation policy will be used to operate the state transition system.

2) Process of Dec-SGTS:

• Phase 1: Local Sub-Goal Tree Search The agent plants a subgoal tree based on the intentions of teammates using discounted UCT (D-UCT).

• Phase 2: Intention Update Use a distributed optimization method to refine intentions based on the current subgoal tree.

• Phase 3: Intention Sharing Use asynchronous communication to transmit intentions between agents.

5. Behavior Tree Communication Algorithm

5.1. Background

In the coordination problem of behavior trees between multiple NPCs, local communication between behavior trees is also a solution. This study discusses local communication between behavior trees. [4] Although the article applies behavior trees in the field of robotics, it is no different from using them in a multi-NPC environment. To reduce direct communication and improve efficient episodic memory management for resource-constrained multi-robot systems, this study introduces two new Behavior Tree (BT) modes: eavesdrop-update and eavesdrop-buffer-update.[4] Traditional direct communication can lead to communication disruption in large swarm clusters and knowledge transfer methods that rely on direct communication may encounter communication throttling issues. To address these problems, the EBU (eavesdrop-buffer-update) mode was developed, allowing agents to store nearby query responses for later updates. Indirect knowledge transfer through behavior trees is called IKT-BT (Indirect Knowledge Transfer Behavior Tree), a new strategy to achieve individual behavior tree-level knowledge expansion through communication with other agents in the group [13].

5.2. Basic Definitions of BT communication

1) Direct Communication and Indirect Communication:

• Direct Communication: One-to-one communication in-volving explicit interaction methods such as Wi-Fi, radio frequencies, etc. Direct communication faces challenges like communication interference, bandwidth bottlenecks, and debugging for each agent.

• Indirect Communication: Information is conveyed by manipulating the environment, such as releasing pheromones, visual cues, observing the actions of other agents, etc. Indirect communication risks information becoming outdated.

2) Eavesdropping:

• Interceptive Eavesdropping: The focus of this study, referring to the interception of already exchanged information.

• Social Eavesdropping: Involves observing the behaviors of other agents to gain information. Figure 6 shows a comparison of the knowledge transfer mechanisms: direct communication (top row) and indirect eavesdropping (bottom row) modalities.

Figure 6. Knowledge transfer mechanisms [4].

3) Intelligent Communication Language (ACL):

• ACL involves the representation, retrieval, sharing, and merging of knowledge. In multi-robot systems (MRS) , it is typically operated through ontology, allowing knowledge to be represented as related and constrained concepts, with functionalities for merging, unifying, and inheriting.

• Relevant systems include the core of CORA, ontology service requests in SO-MRS [14], and the web ontology language OWL.

4) Behavior Trees (BTs):

• Behavior Trees are tick-based structures that traverse the tree each tick [15]. BTs include selector nodes, parallel nodes, decorator nodes, and condition and action nodes. Condition variables are managed by the blackboard, and actions are specified by the action manager.

5) Episodic Memory Buffer Strategy:

• A strategy allowing agents to store and prioritize messages, utilizing knowledge to enhance cognitive and ephemeral long-term behavior in robots.

5.3. Algorithms

1) Representation of Knowledge: Representation of Knowledge Behavior Trees is a mapping from input s to output action a. The return states are threefold: running, success, and failure. The time step is denoted as ∆t. The robot behavior tree includes several components:

The Critical Response Action Tree (Tc), located on the far left of the behavior tree, encompasses critical actions that must be executed. When encountering a critical event, each agent will first attempt to find an appropriate response action from Tc.

The Idle Response Tree (Tf) activates when all left-side subtrees are not executed, covering states such as idle, wait, and other special conditions.

The Common Knowledge (TCK) refers to knowledge shared by all robots, while the Inherent Prior Knowledge (TPK) consists of knowledge each robot possesses before the task begins. Additionally, the New Knowledge Acquired During Tasks (TNK) includes knowledge learned and acquired by robots during task execution.

An Optional Module (Tmod) can be one of TQRA, TQRU, TEU, or TEBU, and operates in parallel with the control tree (Tcontrol).

Finally, the Known State Sequence is used to record and determine the response action sequence of the robot. This sequence helps determine the response action sequence Tka, where Tka is the state-action subtree (knowledge subtree).

2) Concepts of Algorithm: The Query Response concept involves using a knowledge subtree to determine if the robot possesses the relevant knowledge for each query.

Eavesdropping involves capturing data as a triplet containing the message timer value t_m, which is stored in Lbuffer and deleted after a period defined by tm (message discard) .

The Optional Module (Tmod) in the behavior tree can be one of several types:

• TQRA (Query and Response Action): Actions requiring querying and waiting for a response.

• TQRU (Query and Response Update): Actions requiring querying and immediate updating.

• TEU (Eavesdrop and Update): Actions involving im-mediate updates based on eavesdropped information.

• TEBU (Eavesdrop Buffer and Update): Actions that buffer eavesdropped information, updating only when a gap is discovered.

3) Algorithms Realization: The overall query count of QRU is evidently lower than QRA, making it advisable to combine QRU with other algorithms wherever possible.

The first algorithm combines EU with QRU. It continuously checks if the query state sequence sq is present in the listening buffer Lbuffer. If Lbuffer is not empty, for each message meve in Lbuffer, it retrieves the message information s. If s is not in the known state list Lks (i. e. , it is unknown), it retrieves the action subtree Ta of the message, constructs the sequence sq and Ta, merges T_k with Tcontrol at T_K,

adds s to the known state list Lks, and finally adds Ta to the known action list Lka. Then, Lbuffer is cleared. The second algorithm combines EBU with QRU. The updating process is like the first algorithm. However, while the first continuously polls Lbuffer for queries and updates until Lbuffer is empty, the second checks Lbuffer only when there is a query s_q. It can be mathematically proven that the overall query count of indirect communication is lower than direct communication. Furthermore, EBU has fewer update counts compared to EU. Therefore, the algorithm that combines EBU with QRU theoretically performs the best.

5.4. Results and Comparison of Algorithms

In this paper [4], the communication algorithm optimization of the behavior tree is tested by designing robots to collect different types of resources in an obstacle scene and send them to different fixed collection areas. The results show that indirect communication, such as EU and EBU, is better than direct communication, such as QRA and QRU. In general, EU>EBU>QRU>QRA. Under the same communication range, the collection rate of the QRU mode is slower than that of EU and EBU, which can be attributed to the query-response delay within the group. For EU and EBU modes, EU performs slightly better than EBU at lower communication ranges, but both modes show similar trends at larger range values. The updates in EBU that utilize knowledge from the message buffer increase with the increase of communication range, while EU tends to saturation. Although EU performs better than EBU, when memory constraints are imposed, the EBU group effectively converts information from messages to knowledge as needed, rather than unnecessarily updating its knowledge, which may never be used. Therefore, EBU and EU each have their own advantages and disadvantages.

6. Conclusion

6.1. Summary of Three Directions

1) Optimization of Behavior Tree: Emotional behavior tree and event-driven behavior tree are both strategies to optimize the behavior tree itself, but they each have different advantages. The implementation of emotional behavior tree improves the realism and interactivity of NPC behavior, and makes NPC more intelligent, but it lacks the cooperation between multiple NPCs. The event-driven behavior tree im-proves the interaction and cooperation between multiple NPCs by dynamically responding to external events. If these two optimization strategies can be combined, a more intelligent and flexible behavior tree model can be developed. For example, sentiment selectors are added to the structure of EDBT.

2) Behavior Tree Search Algorithms: The behavior tree search algorithms were employed to find an optimal action sequence for agents to execute. Due to the dynamic nature of the decision-making process, researchers cannot simply use classic tree search methods for selection. Therefore, they applied the Monte Carlo tree search algorithm to address the optimization problem. The final algorithm mentioned in this section, Dec-SGTS, integrates multiple techniques, evolving from Dec-MCTS, a classic algorithm for Markov decision process problems. Dec-SGTS not only uses the Monte Carlo tree search to update state trees but also employs a sub-goal protocol to enhance modularity and semantics, making the decision-making process more akin to that of humans.

3) Behavior Tree Communication Algorithm: This study explores the use of local communication in behavior trees to solve the coordination problem between behavior trees in multi-NPC environments, drawing on applications in the field of robotics. To reduce the problems caused by direct communication and improve the efficiency of resource-constrained systems, two new behavior tree modes are introduced: eavesdropping update (EU) and eavesdropping buffer update (EBU). Traditional direct communication is prone to communication interruptions and bandwidth bottlenecks, while the EBU mode allows agents to store nearby query responses for update when needed, thereby achieving indirect knowledge transfer [4] (IKT-BT). Behavior trees play a key role in this process, managing different nodes and conditions through a structured tick mechanism. Experimental results show that indirect communication modes outperform direct communication modes in performance, especially in large groups, where EU and EBU can effectively utilize information in the eavesdropping buffer to achieve more efficient knowledge update and transfer. Overall, although EU performs slightly better in low communication range, EBU shows better adapt-ability and efficiency by selectively updating knowledge when memory is limited. Therefore, EU and EBU each have their own advantages, and the appropriate mode can be selected according to needs in specific applications.

6.2. Scenarios for the Applicability of Three Directions

The system combining Emotional behavior Tree (EmoBT) and Event-driven behavior Tree (EDBT) is highly adaptable and dynamic responsive, especially suitable for complex and dynamic game scenarios. These systems can adapt agent behavior based on emotional states and real-time events to enhance the game experience. Based on the characteristics of Monte Carlo tree search algorithm, which include being dynamic, decentralized, and making decisions step by step, this improvement is particularly effective in systems with many agents. The game process should be long enough to allow agents to learn and improve. Additionally, during the game, there should be certain behaviors (decision directions) that may not align with immediate benefits but are in line with ultimate and collective benefits. Optimizing the communication algorithms between behavior trees, however, is necessary when agents require high levels of coordination, need to share state or information, or when it is crucial to avoid communication bottlenecks and delays.

6.3. Limitations and Future Works

Although this study has made some progress in the application and optimization of behavior tree technology, there are still some limitations and shortcomings. For instance, the integration of emotional behavior trees and event-driven behavior trees has not yet been extensively tested and validated in actual systems, and their effectiveness and potential issues in complex systems require further investigation. Additionally, the robustness of the current behavior tree search algorithms in handling extreme cases and abnormal states needs to be improved. For behavior tree communication algorithms, how to ensure communication efficiency while securing the accuracy and safety of information is also an important direction for future research. Future research could delve into the following areas: first, exploring the deep integration of emotional behavior trees and event-driven behavior trees to assess their performance in various gaming and simulation environments; second, developing more efficient behavior tree search algorithms to enhance decision-making speed and accuracy in dynamic and uncertain environments; and lastly, optimizing behavior tree communication algorithms, especially for use in multi-agent systems, to improve their performance in large-scale real-time systems.

Acknowledgement

Chenyu Hu, Ruiyuan Wu, Xiaojie Deng contributed equally to this work and should be considered co-first authors.