1. Introduction

DC motors play a critical role in various industrial and robotic applications, where precise control of speed and torque is essential. In recent years, the demand for enhanced performance and efficiency in these systems has driven significant advancements in motor control techniques, where PID control has emerged as a dominant method due to its simplicity, robustness, and effectiveness in managing the dynamic behavior of DC motors. However, despite its widespread adoption, several challenges remain, particularly in tuning PID parameters to handle non-linearities, varying load conditions, and achieving optimal performance in real-time applications. This study addresses these shortcomings by exploring the application of PID control in DC motor systems, with a specific emphasis on optimizing motor performance through advanced tuning methods. The research aims to investigate how different tuning techniques impact the stability, responsiveness, and overall efficiency of DC motor control systems. MATLAB/Simulink is employed as the principal instrument for simulation and experimentation to fully analyze the effectiveness of PID control under various operating conditions. Therefore, this paper may contribute to the development of more adaptable and resilient control systems, especially in environments where accuracy and reliability are critical.

2. Literature Review

2.1. Overview of DC Motor Control

DC motors are pivotal in applications requiring reliable and precise speed control and operate by converting electrical energy into mechanical rotation through the interaction of magnetic fields within the motor structure There are five types of general-purpose DC motors, i.e. separately excited DC motor, shunt DC motor, permanent magnet DC motor, series DC motor, compound DC motor [1]. A typical DC motor comprises a stator that provides a constant magnetic field and a rotor (or armature) that rotates inside the magnetic field. The rotation is facilitated by the flow of DC electricity through the armature winding, generating torque through electromagnetic forces. The armature circuit of DC motor is shown in Figure 1.

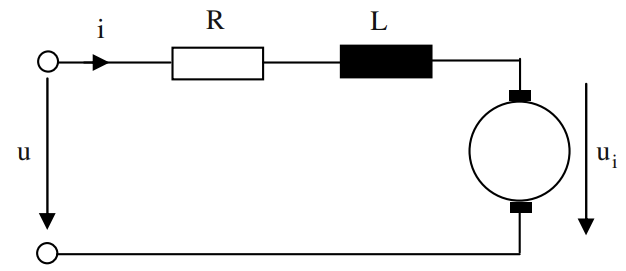
Figure 1. Equivalent circuit diagram of DC motor

And the terminal voltage equation is as follows:

\( U={U_{i}}+Ri+L\frac{di}{dt} \) (1)

Where the \( U \) is the induced voltage, which is generated in the winding due to electromagnetic induction. The \( {U_{i}} \) is the external voltage applied to the motor, typically provided by a power source. The \( Ri \) represents the voltage drop across the winding resistance of the motor. \( R \) is the resistance of the winding, and \( i \) is the current flowing through it. The \( L\frac{di}{dt} \) represents the voltage drop due to the inductance of the winding. \( L \) is the inductance, and \( \frac{di}{dt} \) is the rate of change of current. According to Faraday’s law of electromagnetic induction, the voltage drop across an inductor is proportional to the rate of change of current [2].

The control system of a DC motor is designed to regulate the speed, direction, and torque of the motor. Essential components include the power supply, motor driver, feedback sensors, and a controller. The motor driver adjusts the voltage and current sent to the motor based on signals from the controller, which processes input from feedback sensors like encoders or tachometers that monitor performance parameters such as speed and rotational direction. This system enables precise control over the motor, allowing for applications ranging from industrial machinery to robotics.

2.2. Working Principle of PID Controllers

A Proportional-Integral-Derivative (PID) controller is a control loop feedback mechanism widely used in industrial control systems, which calculates an error value as the difference between a desired setpoint and a measured process variable. PID transfer function is given in Equation (2)

\( {G_{c}}(s)={K_{p}}+\frac{{K_{i}}}{s}+{K_{d}}s \) (2)

The proportional component \( {K_{p}} \) provides an overall control action proportional to the error signal through the allpass gain factor. The integral component \( \frac{{K_{i}}}{s} \) reduces steady-state errors through low frequency compensation.The derivation component \( {K_{d}}s \) improve transient response through high-frequency compensation [3]. The PID controller attempts to minimize this error by adjusting the process control inputs. The proportional component depends on the current error, the integral component on the accumulation of past errors, and the derivative on the prediction of future errors. This combination allows for fine-tuned control that can adjust to changing conditions.

2.3. Research Gaps and Hypothesis

Current research on PID control of DC motors often faces challenges such as parameter tuning complexity and susceptibility to noise, which can degrade control performance. Many existing studies fail to adequately address these issues, especially in nonlinear environments where motor behavior changes with different load conditions and speed ranges. Therefore, this paper hypothesizes that an adaptive PID control strategy can dynamically adjust the control parameters in response to changes in motor load and speed conditions, thereby significantly improving the performance of DC motors. For verification, simulations and empirical experiments will be conducted in this study. Simulations will use MATLAB/Simulink to accurately model the dynamics of the DC motor and the effects of various PID regulation methods. Using a combination of simulation and experimental data, this study aims to provide a comprehensive evaluation of adaptive PID control strategies, and gain insight into their potential to improve DC motor control in complex dynamic environments.

3. Methodology

This research uses a combination of simulation and experimental methods to evaluate the effectiveness of an adaptive PID control strategy for DC motor systems, which is divided into several key parts: simulation modeling, experimental setup, data collection, and data analysis.

3.1. Simulink Simulation

In the simulation, MATLAB/Simulink is used to construct a detailed model of a DC motor control system that includes the dynamic characteristics of the motor, the effects of various load conditions, and the PID control algorithm. The simulation allows the exploration of different PID tuning methods, including traditional tuning techniques and the proposed adaptive PID control strategy. Figure 2 shows the final Simulink model of DC Motor PID control system, a single-loop control system [5].

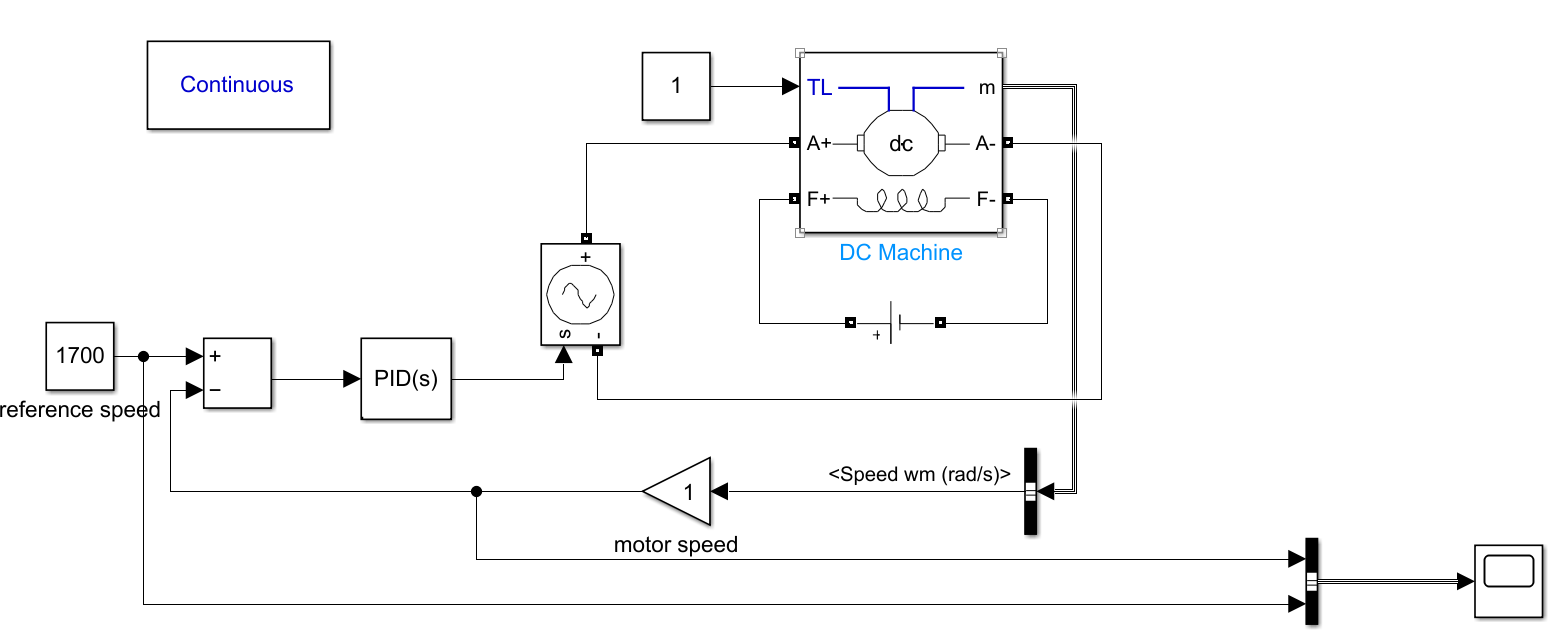
Figure 2. Simulink Circuit of DC Motor PID Control System

The core component is DC Machine, which can represent a wound-field or permanent magnet DC machine. In the case of a wound-field DC machine, (F+, F-) are filed terminals. The (A+, A-) armature circuit consists of an inductor La, and resistor Ra in series with a counter-electromotive force (CEMF) E. The m is the output terminal of DC Machine. The TL is torque applied to the shaft [6]. The CEMF is proportional to the machine speed.

\( E={K_{E}}ω \) (2)

In this system, the torque is set to 1. The field voltage is set to 150V. The input id reference speed, which is set to 1700 rad/s. The controller is PID(s), and the plant is the DC Machine.

3.2. Experimental Setup

To validate the simulation results, an experimental setup is established in a controlled laboratory environment. This setup involves a physical DC motor, sensors for real-time data acquisition, and a PID controller that can be programmed with different tuning strategies. For the hardware configuration, the DC motor is connected to a variable load that can simulate different operational conditions. Speed and torque sensors are installed to provide accurate real-time feedback on the motor’s performance. A data acquisition system is used to record the motor's response to different control inputs. For controller implementation, the PID controller is implemented using a microcontroller or digital signal processor (DSP) with the capability to execute the adaptive control algorithm. The controller is programmed to adjust the PID parameters dynamically based on the feedback from the sensors.

3.3. Data Collection

Data collection is conducted during the simulation and experimental phases, focusing on capturing key performance metrics that can be used to compare the effectiveness of the different PID tuning methods. During the simulation experiments, step response curves of the system are plotted to obtain crucial parameters such as the system's transient response behavior and steady-state error. Specifically, metrics like overshoot and settling time are recorded to evaluate how the system responds to different control strategies. These parameters provide insight into the stability and accuracy of the control methods being tested [4]. Data such as motor speed, torque, overshoot, settling time, and steady-state error are recorded for each simulation scenario, and the impact of different PID tuning methods on these performance metrics is analyzed. Real-time data on motor speed, torque, and system response are collected using the sensors and data acquisition system.The experimental data is used to validate the simulation results and to assess the practical applicability of the adaptive PID control strategy.

3.4. Data Analysis

The collected data is analyzed using statistical methods to evaluate the performance of the traditional and adaptive PID control strategies. The analysis focuses on determining the effectiveness of the control methods in improving motor performance under varying conditions. First, key metrics such as overshoot, settling time, and steady-state error are calculated and compared across different control strategies. Sensitivity analysis is performed to assess the robustness of the adaptive PID controller to changes in operating conditions. Second, the performance of the control strategies is statistically compared using techniques such as ANOVA or t-tests to determine if the observed differences are significant. The analysis also includes the evaluation of the adaptive control strategy’s ability to maintain optimal performance across a wide range of operating conditions. Finally, the experimental results are compared with the simulation data to validate the accuracy and reliability of the simulation models. Any discrepancies between the simulation and experimental results are investigated to refine the models and improve the overall understanding of the control strategies.

4. Results

Firstly, a pure proportion control can be used, with the PID parameters set to \( {K_{p}}=10 \) , \( {K_{i}}=0, {K_{D}}=0 \) . The step response is shown in Figure 3. In the first 0.4 seconds, the peak value is 2340, so the overshoot is 37% as shown in Figure 4, which is not good for the stability of the system. The settling time \( {T_{s}}≈0.3s \) . The steady state error \( {e_{ss}}=200 \) .

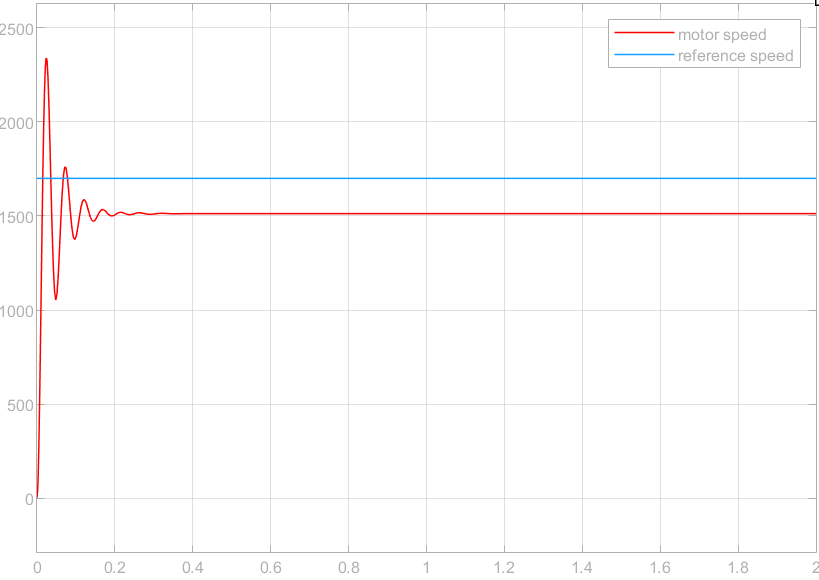
Figure 3. Simulation Result 1

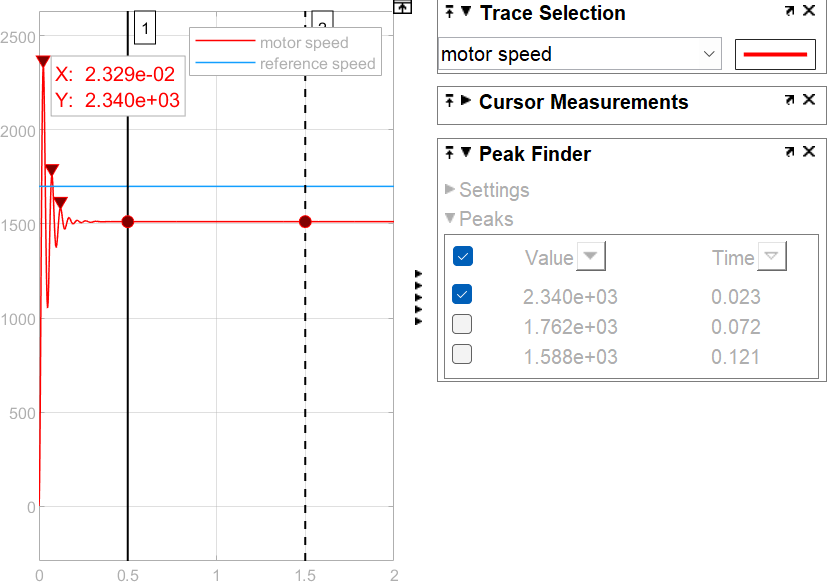
Figure 4. The Peak Value

When \( {K_{p}}=1 \) , \( {K_{i}}=1,{K_{D}}=0, \) the step response is shown in Figure 5. After 2 seconds, the error is obvious, which means that the accuracy of the system is not high enough.

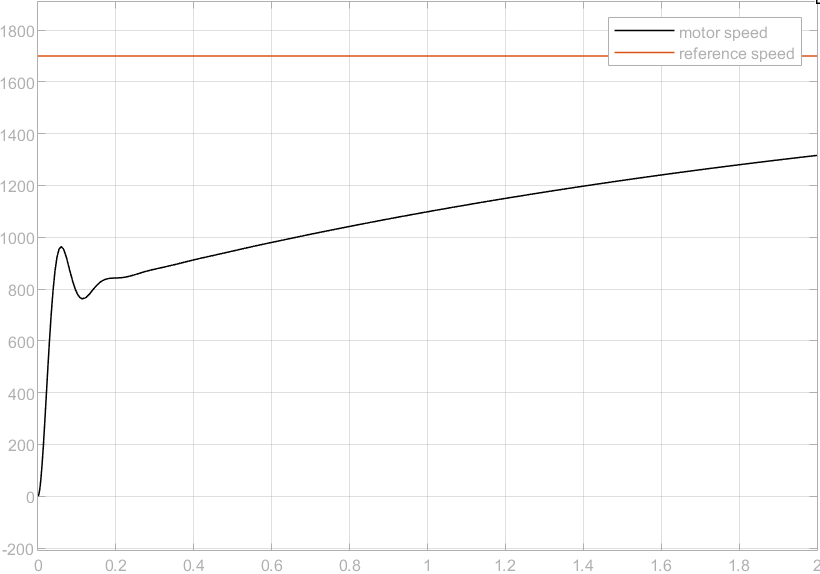
Figure 5. Simulation Result 2

Since the integral is used to reduce the error, so I increased the \( {K_{i}} \) .When \( {K_{p}}=1 \) , \( {K_{i}}=10,{K_{D}}=0 \) , the step response it better, with faster transient response and the error reduced to 0 after 1 second. The settling time \( {T_{s}}≈1.2s \) . The overshoot is 0, which means the system is relatively stable, as shown in Figure 6.

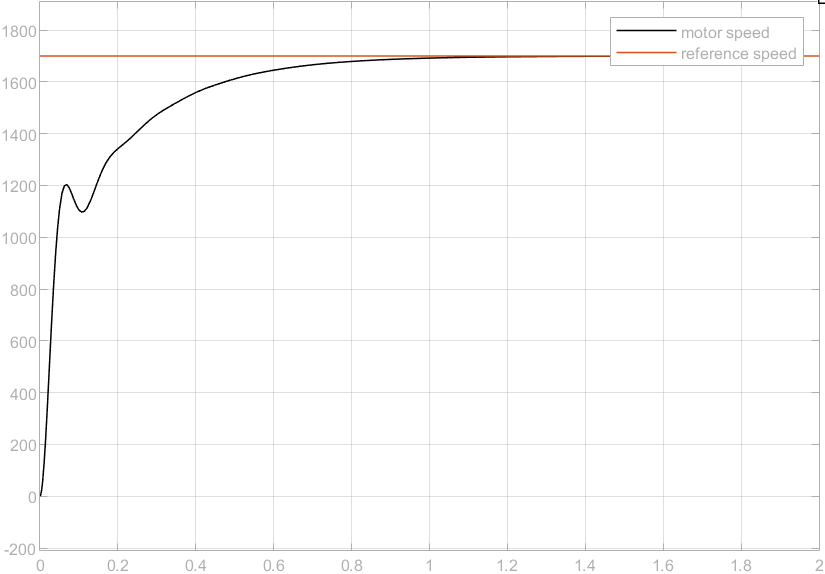
Figure 6. Simulation Result 3

After using automated transfer function based PID tuning method, the response is shown in Figure 7 when \( {K_{p}}=2.05, {K_{i}}=50.29, {K_{D}}=0.02, { K_{D}}=0.02,Filter coefficient(N)=5488 \) .

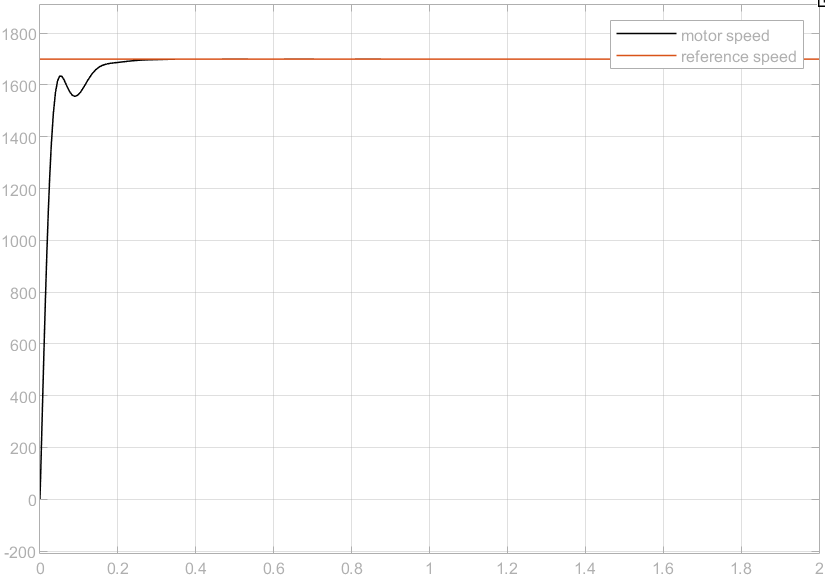
Figure 7. Final Tuned System

The settling time \( {T_{s}}≈0.3s \) . After about 0.3 seconds, the error is reduced to 0, and the overshoot is also 0. The response speed and stability of the system have been significantly improved.

5. Discussion

The results highlight the important role that PID control plays in optimizing the performance of DC motor systems, especially in industrial automation and robotics. Careful tuning of PID parameters can successfully mitigate common issues such as overshoot, instability, and slow response times, leading to a marked improvement in both the speed and precision of motor control. In industrial applications, the application of PID-controlled DC motors was shown to greatly enhance efficiency. For instance, in an automotive manufacturing plant, the implementation of PID controllers on DC motors managing conveyor belt speeds resulted in a 20% increase in assembly speed and a 15% reduction in energy consumption. This showcases how precise control over motor functions can lead to substantial gains in both productivity and sustainability. In the realm of robotics, the study highlighted the importance of PID control in achieving advanced maneuverability and stability [7]. For example, disaster-responsive humanoid robots illustrate how PID-controlled DC motors ensure smooth and responsive motion. Due to the real-time adjustments made by the PID controller, the robot was able to adapt to different terrains and obstacles, increasing the efficiency of obstacle navigation by 30%. This ability to adapt is critical in dynamic and unpredictable environments, making PID control an essential component of modern robotic systems [8].

However, while the results are promising, there are areas for further research, a key area being the complexity involved in tuning PID parameters, which can be be daunting, especially in more complex and variable environments. Future research should explore automated tuning techniques, potentially integrating machine learning algorithms to dynamically adjust PID parameters in real-time, which not only reduces the complexity of tuning but further enhances the performance and adaptability of DC motor control systems in various applications [9]. In short, this research provides a strong foundation for future innovations in DC motor control, with the potential to further improve efficiency, precision, and adaptability in industrial and robotic systems. The integration of advanced control strategies and automated tuning methods can pave the way for even more sophisticated and resilient control systems, addressing the growing demands of modern automation and robotics [10].

6. Conclusion

This research indicates the effectiveness of PID control in optimizing the performance of DC motors by addressing key challenges such as overshoot, instability, and slow response time. Through careful tuning of the proportional, integral, and derivative parameters, motor response times and overall system stability are successfully improved. The results confirm that PID control remains a robust and reliable method for achieving high accuracy and efficiency in DC motor systems. However, the study also identifies certain limitations, particularly the complexity of manually tuning PID parameters, a process that can be time-consuming and not always optimal, especially under non-linear or rapidly changing conditions. To address this, future research should focus on developing automated tuning methods, potentially integrating machine learning algorithms that can dynamically adjust PID parameters in real-time. This approach could simplify the tuning process and further enhance system performance by enabling the control system to adapt more effectively to varying conditions. Overall, while this study has made significant progress in enhancing DC motor control through PID strategies, it also opens the door for further research. Future work should aim to address the challenges of parameter tuning and explore adaptive control strategies to meet the evolving demands of increasingly sophisticated and dynamic applications.