1. Introduction

Gomoku is a traditional board game that has captured the interest of players worldwide due to its simple rules and deep strategic complexity. Although it is not as complex as chess and Go, Gomoku presents significant challenges in terms of strategic planning and move prediction. The objective is to be the first to align five stones of the same color in a row, either horizontally, vertically, or diagonally, on a 15x15 board. This game has a rich history and is played in both casual and competitive settings, with various rule sets that add complexity, such as the "forbidden move" rules in competitive play to balance the advantage of the first player.

The development of artificial intelligence (AI) for Gomoku has progressed significantly, particularly with the advent of advanced search algorithms and machine learning techniques. One prominent approach is using Alpha-Beta Pruning. Alpha-Beta Pruning is a search technique that speeds up the decision-making process by reducing the number of nodes evaluated in the game tree without compromising the accuracy of finding the optimal move. By pruning branches that do not need to be explored, the algorithm can more efficiently identify the best possible moves [1, 2].

The use of Alpha-Beta Pruning in Gomoku AI offers several advantages. First, it is computationally efficient, making it suitable for real-time game decision-makin. This efficiency is crucial for Gomoku, where the number of possible moves increases exponentially with the board's size and the progression of the game [3, 4]. Second, Alpha-Beta Pruning can be easily combined with value evaluation algorithm to evaluate the desirability of different board states, allowing the AI to focus on promising lines of play [5]. Value evaluation algorithm can be designed based on various factors, such as the number of consecutive stones in a row, potential threats from the opponent, and defensive strategies. These algorithms help the AI not only to search more efficiently but also to simulate a more human-like approach [6, 7].

Moreover, the application of Alpha-Beta Pruning in Gomoku AI provides a foundation for further enhancement using machine learning techniques. For instance, deep learning techniques can help refine the evaluation function used by the Alpha-Beta algorithm. This combination can lead to a more nuanced understanding of game states, as deep learning models can learn complex patterns and strategies from a large dataset of historical games [8]. Additionally, reinforcement learning can be used to train the AI through self-play, continuously improving its performance by learning from past experiences and adjusting its strategies accordingly [9].

In recent years, the success of AI systems like AlphaGo, which defeated human champions in the game of Go, has demonstrated the potential of combining traditional search algorithms with machine learning techniques [10]. While Gomoku has a simpler rule set compared to Go, the challenges it presents are significant enough to warrant a similar approach. The development of a Gomoku AI using Alpha-Beta Pruning not only contributes to the field of game AI but also provides insights into efficient problem-solving techniques applicable to other domains.

This paper explores the implementation of a Gomoku AI using the Alpha-Beta Pruning search algorithm. This paper will discuss the basic principles of the Alpha-Beta Pruning technique, its integration with value evaluation algorithm, and potential enhancements using machine learning. Through this exploration, this paper aims to demonstrate how a traditional search algorithm can be adapted and enhanced to tackle the strategic challenges posed by Gomoku, providing a robust and efficient AI solution for this timeless game.

2. Methodology

2.1. Minimax algorithm

The Minimax algorithm is a depth-first search algorithm used in zero-sum games, where the total benefit for both parties is zero. This means that when one party gains an advantage, the other party loses an equal amount. In the set of possible moves, each player will choose the move that best for them and worst for their opponent. The game between the two parties can be represented as a decision tree. If the current level is the player's decision state, the player will choose the node that maximizes their benefit, which is called the MAX level. If the current level is the opponent's decision state, the player will choose the path that minimizes the opponent's benefit, which is called the MIN level.

Thus, in the constructed decision tree, the nodes can be classified as MAX nodes (in the MAX level), MIN nodes (in the MIN level), and the leaf nodes. Each leaf node is scored by an evaluation function, and then the values are assigned to each node from bottom to top. MAX nodes take the maximum value among their child nodes as their current value, while MIN nodes take the minimum value among their child nodes as their current value.

For example, here is a three-tier game tree with the square representing the first hand (choosing the most valued situation) and the circle representing the second hand (choosing the least valued situation), and the estimated values of the leaf nodes are 3, 15, 2, 14, 0, 14, 5, 7. In the MAX layer the largest child node is selected, while the smallest child node is chosen in the MIN layer. Ultimately, the search targets the leaf node with a value of 14 (Figure 1).

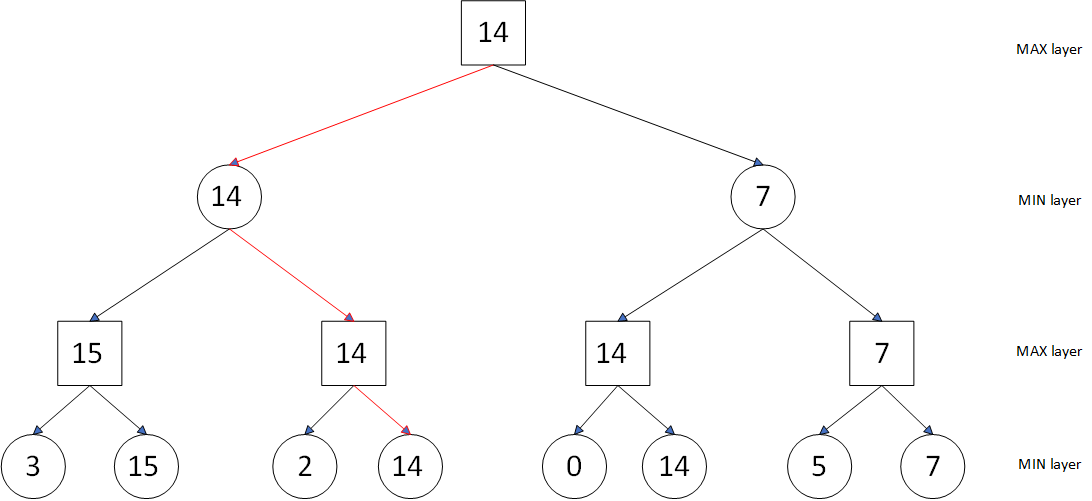
Figure 1. Minimax Algorithm Diagram

2.2. Negamax algorithm

The Negamax algorithm is a variation of the Minimax algorithm, simplified by taking advantage of the zero-sum nature of games like Gomoku. For the player, the best strategy is equal to the opponent's worst strategy. Thus, by negating the payoff of the opponent, that is, converting the minimum to the negative of the opponent's maximum, the problem can be transformed into a maximization search problem. For example, here is a three-tier game tree with the same leaf nodes as Figure 1 and 2. But in this tree there is only the MAX layer. In each layer, the largest child node is selected, its value is negated, and the resulting negative number is then propagated to the parent node. Ultimately, the search still targets the leaf node with a value of 14.

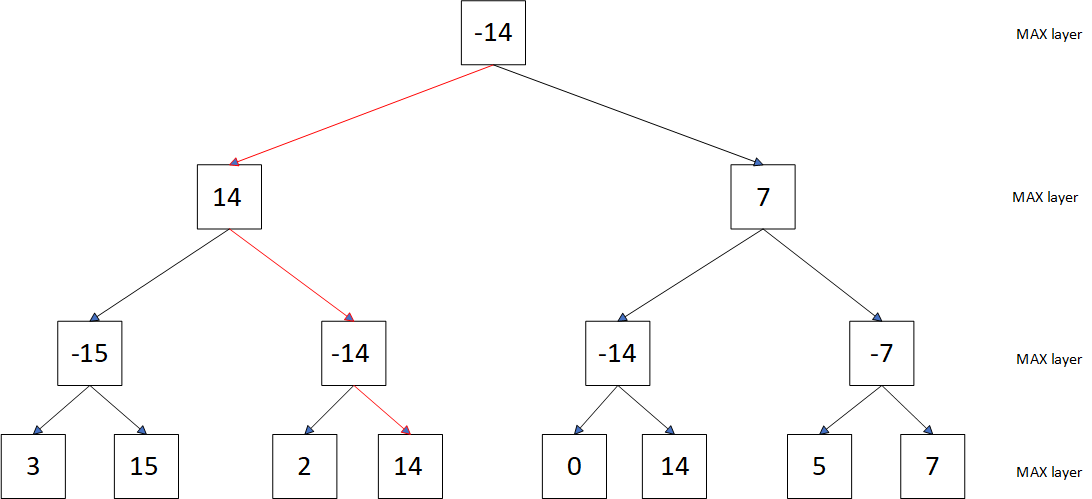
Figure 2. Negamax Algorithm Diagram

2.3. Alpha-beta pruning algorithm

The Alpha-Beta Pruning algorithm is an enhancement of the Minimax algorithm that significantly improves computational efficiency by reducing the nodes evaluated in the search tree (Table 1). Alpha represents the lower limit of the current node, and Beta represents the upper limit. During the traversal of the search tree, if the Alpha value of a node is greater than or equal to the Beta value, then the subtree of the node does not need to be searched again, because the value passed down from the parent node is already greater than or equal to (or less than or equal to) a larger (or smaller) value, which can no longer affect the answer. When implemented, the α and β values are continuously updated to the child node, and after the child node has been searched back to the parent node to continue updating the α and β values (Figure 3).

Table 1. Alpha-Beta Pruning Algorithm

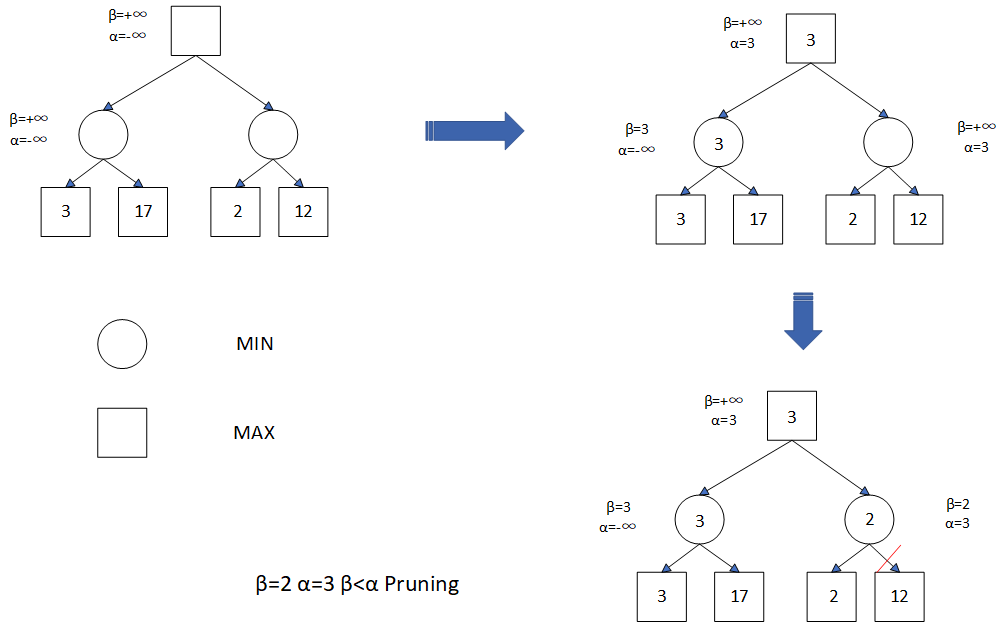
Figure 3. Alpha-Beta Pruning Algorithm

3. Results and discussion

3.1. Value evaluation function

The value evaluation function is designed to assess the board state at any given point in the game. It calculates a score based according to the current positions on the board, helping the AI decide the most advantageous move. The scoring rules are shown in the table 2 below. The AI finds the score shape by traversing the entire board, calculates its score against the opponent based on the score shape, and the value is its score minus the opponent's score.

Table 2. Score Rule

3.2. Search algorithm

The search algorithm is a vital part of the Gomoku AI, responsible for evaluating potential moves and determining the optimal strategy. The algorithm employed in the AI is a combination of the Negamax algorithm with Alpha-Beta pruning. Given the search depth and the state of the board, the AI traverses all possible moves and simulates the state of the game after each move. When the search depth is reached or the tie is out, AI calculates the score by the value evaluation function, constructs a search tree with the Negamax Algorithm, uses Alpha-Beta Pruning Algorithm to improve the search efficiency and finally find the best drop point. Additionally, in the search process, AI will give priority to searching the grid around the spot on the checkerboard, triggering the pruning operation earlier to improve efficiency.

3.3. AI performance

The implementation of the Alpha-Beta Pruning algorithm within the Gomoku AI provided significant improvements in both computational efficiency and the quality of move selection. The algorithm was tested by simulating multiple games between the AI and a human player. One of the key metrics evaluated was the number of AI search nodes, which directly correlates with the AI’s response time.

Consider the Gomoku illustrated in Figure 4, where the AI controls the white chess, and the human player controls the black chess. It is evident that with a search depth set to 3, the AI is capable of defeating players with a certain level of proficiency. Moreover, the implementation of the pruning in the Gomoku AI markedly enhances the efficiency of the decision-making process. As depicted in Figure 5, the number of searches conducted by the Gomoku AI can reach several thousand, with the pruning action becoming more frequent and increasing progressively with the number of games played. By employing the Alpha-Beta Pruning algorithm, the computation time for the Gomoku AI can be maintained within 2 seconds, significantly improving the AI's decision-making speed.

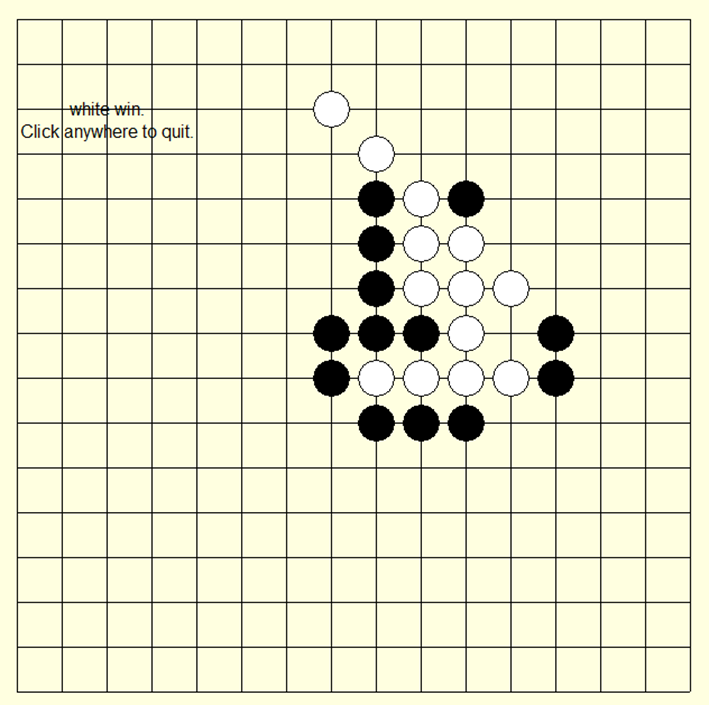
Figure 4. Human vs AI Gameplay Interface

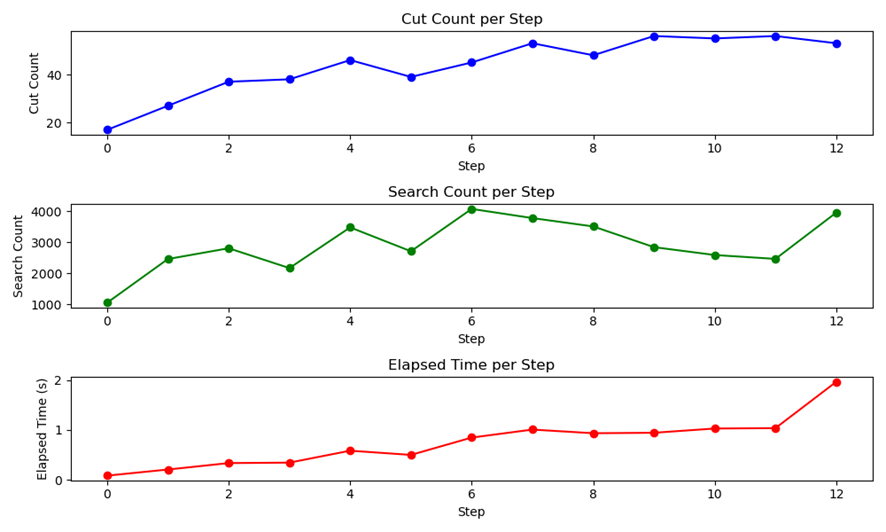
Figure 5. Algorithm Performance Efficiency

4. Discussion

4.1. Limitations

The primary limitation of the current AI search algorithm is its computational complexity. As the search depth increases, the number of possible game states grows exponentially. This results in significant computational time, especially when the depth is set to a higher value to achieve better accuracy and performance.

Also, the algorithm uses a fixed search depth, which means it does not adapt based as the game progresses. In some situations, a deeper search might be necessary, while in others, a shallow search would suffice. This lack of flexibility can either lead to unnecessary computation or suboptimal decision-making.

4.2. Potential improvements

Potential improvements for the AI algorithm focus on incorporating reinforcement learning (RL) techniques. By integrating RL, the AI could learn from past games, adapting its strategies to improve performance over time. Unlike traditional search algorithms, which rely on predefined evaluation functions, an RL-based approach would enable the AI to develop its own evaluation criteria by maximizing cumulative rewards. This could result in a more sophisticated decision-making process, allowing the AI to handle complex game situations more effectively. Additionally, combining RL with deep learning could further enhance the AI's ability to recognize patterns and make more accurate predictions, leading to a more robust Gomoku AI.

5. Conclusion

This paper presents the implementation of a Gomoku AI utilizing the Alpha-Beta pruning algorithm combined with the Negamax algorithm, achieving a balance between computational efficiency and accuracy in move selection. With a search depth of 3, the AI successfully outperforms opponents with moderate skill levels. And the operation of pruning algorithm greatly improves the search efficiency, and the calculation time of AI is controlled within 2 seconds. However, limitations such as fixed search depth and increasing computational complexity as the game progresses are significant challenges. These constraints can lead to suboptimal decisions or unnecessary computations depending on the game state. Despite these limitations, there is considerable potential for further enhancement. By incorporating reinforcement learning (RL) and deep learning techniques, the AI could adapt its strategies through self-play, improving its performance over time. This integration would enable the system to make more flexible and right decisions. Such advancements not only improve the Gomoku AI’s strategic capabilities, but also provide valuable insights in other real-time decision-making tasks within games and other domains.