1. Introduction

Multilayer films and glasses are pivotal in modern materials science, finding extensive applications across fields such as architecture, electronics, and optics. These technologies leverage the principle of coating surfaces with multiple film layers to tailor optical and thermal properties, such as controlling the light's reflection, transmission, and absorption. In the realm of architecture, multilayer glass, enhanced by multilayer film techniques, offers superior thermal insulation and UV protection. This advancement is crucial as it aligns with the escalating push towards green building practices and energy efficiency [1,2,3].

Current Research Status: The challenge of controlling ultraviolet transmission through multilayer films and glasses is not merely a matter of enhancing indoor comfort but is also critical for health protection, shielding against the harmful effects of UV rays on skin and eyes. The nonlinear dynamics of light transmission through these materials, influenced by various factors across a spectrum of sunlight wavelengths, makes a single analytical model insufficient. Recent advancements in optimization algorithms like particle swarm optimization (PSO) have shown promise in tackling such complex, nonlinear issues effectively. Notable applications include its use by M. H. P. Swari to significantly enhance prediction accuracy in system components availability [4,5], and by W. Fei, who combined it with gray wolf optimization to improve path planning in robotics [6], showcasing the algorithm’s robustness and adaptability in diverse fields.

Study Content: This paper focuses on designing a three-layer window glass structure to minimize UV transmission into indoor spaces, optimizing the thickness of each layer using particle swarm optimization (PSO). The study constructs a model to calculate UV transmittance specifically in the 300-400 nm range, utilizing this model as a fitness function in the PSO process. The algorithm aids in exploring the complex variable space to pinpoint the optimal thickness configuration that minimizes UV penetration. Detailed discussions in the paper will cover the fundamentals of PSO, its application in this research, the development of the optimization model, and a comparative analysis of the experimental results against traditional glass designs. The conclusion will synthesize the findings and propose directions for future research, aiming to further enhance the efficiency and application of multilayer glass technology in sustainable building designs [7,8].

2. Method Introduction

The optimal solution for the glass thickness combination is found in this work by applying particle swarm optimization. PSO, or particle swarm optimization, is a swarm intelligence program that finds the best answer based on studies on avian predators. Searching the region surrounding the bird that is closest to the food is the easiest and most efficient way for birds to find food [9]. PSO is inspired from this and guides the search direction of individuals through information sharing among individuals in the group. So as to achieve the purpose of optimization.

2.1. Basic principles of pSO

The steps involved in particle swarm optimization are as follows:

Set the beginning position and velocity of the particle swarm to a random value, and use the best position that each particle has ever had in the past for each particle. Fitness function is calculated to obtain the fitness value, and its value indicates the quality of the particle.

Consider a D-dimensional search space with n particles in its population:

\( X=({X_{1}}{,X_{2}}{,...,X_{n}}) \) (1)

A D-dimensional vector is represented by each particle:

\( {{X_{i}}=({X_{i1}}{,X_{i2}}{,...,X_{iD}})^{T}} \) (2)

The i-th particle's velocity is:

\( {{V_{i}}=({V_{i1}}{,V_{i2}}{,...,V_{iD}})^{T}} \) (3)

Individual extreme value:

\( {{P_{i}}=({P_{i1}}{,P_{i2}}{,...,P_{iD}})^{T}} \) (4)

Group extreme value:

\( {{P_{g}}=({P_{g1}}{,P_{g2}}{,...,P_{gD}})^{T}} \) (5)

Iterative update: For each particle, update its speed and position according to the velocity update formula and position update formula.

Speed update formula:

\( V_{id}^{k+1}=ωV_{id}^{k}+{c_{1}}{r_{1}}(P_{id}^{k}-X_{id}^{k}){{c_{2}}r_{2}}(P_{id}^{k}-X_{id}^{k}) \) (6)

Location update formula:

\( X_{id}^{k+1}=X_{id}^{k}+V_{id}^{k+1} \) (7)

The one that regulates the continuity of particle velocity is \( ω \) , which is the inertia weight. The algorithm is capable of balancing both local and global search by modifying the inertia weight. If the inertia weight is smaller, local search is facilitated, whereas global search is facilitated by a larger inertia weight;

\( k \) is the quantity of present iterations;

\( {c_{1}} \) and \( {c_{2}} \) are non-negative constants. \( {c_{1}} \) measures the degree of dependence of particles on their own historical best position (individual experience). Greater \( {c_{1}} \) will make particles more inclined to return to their own best position. \( {c_{2}} \) measures the degree of dependence of particles on the optimal position of the group (group experience), and larger particles typically gravitate toward the group's ideal location;

\( {r_{1}} \) and \( {r_{2}} \) are dispersed at random intervals in [0,1]. At the same time, the particle position and speed are limited to a certain interval to prevent blind search.

Individual best and group best update: Particles update their individual best position and group best position in each iteration by comparing their current fitness value to their previous best fitness value. Update the individual best to the present place if the fitness value is greater now than it was in the past. In the meantime, the algorithm compares each person's best fitness value to update the group's optimal position. This mechanism ensures that particle swarm can share information and utilize collective intelligence to accelerate convergence to the optimal solution. This dual update strategy combines the advantages of local search and global search: individual best updates drive particles to find better solutions in their personal historical experience, while group best updates utilize collective experience to guide particles towards the global best solution. This synergistic effect enables particle swarm optimization algorithm to perform well in multivariate optimization problems, effectively avoiding local extremum traps and improving global search capabilities. The particle swarm optimization approach may swiftly identify the best solution in a complicated solution space by iterating and updating generation by generation.

Termination condition: The algorithm terminates when the global optimal fitness value hits a predefined threshold or when the maximum number of iterations is reached. then lastly produce the finished goods.

2.2. Algorithm parameter setting

\( {c_{1}} \) and \( {c_{2}} \) are set to 1.49445. In the particle swarm optimization algorithm, they operate as convergence factors and are set at 1.49445, a value derived from theoretical analysis and extensive experimental validation [10]. This can effectively balance exploration and development, ensuring the stability and efficiency of PSO.

The number of evolution is positioned to 300. 300 iterations are usually sufficient for particle swarm optimization to find and converge to a better solution, while avoiding excessive waste of computational resources.

The population size is set to 20. Setting it to 20 can reduce computational complexity while maintaining diversity. A smaller population size may lead to local optima, while a larger size increases computation time and resources.

The velocity range is [-0.001,0.001] and the position range is [0.003,0.010]. Setting the speed range smaller helps with detailed search and improves the accuracy of the solution. The position range can ensure that the solution is within a reasonable and practical range, that is, within the actual thickness range of the glass used. According to the research of Yasin, F. et al., the width of window glass is generally 5-6mm, and 6mm window glass has relatively good anti-ultraviolet transmission performance. In this study, the search range was expanded to 3-10mm to ensure that the multi-layer glass structure has better UV-weakening properties [11].

3. Building the Multilayer Glass Model

3.1. Glass structure

Since ultraviolet light with a wavelength below 400nm is harmful to health, this study selected three layers of glass as building window glass, and used particle swarm optimization (PSO) to optimize the thickness of each layer (L1, L2, L3), so that the least ultraviolet light can enter the room, that is, to reduce the transmittance of ultraviolet band. To bolster the protective effect, two air layers are positioned between the glass layers, creating a five-layer composite structure. This design not only optimizes UV blocking but also enhances thermal and acoustic insulation properties. The first layer of glass incorporates ultraviolet absorbing materials, substantially reducing the initial transmission of UV rays; The first air layer acts as a thermal shield, reducing heat transfer and enhancing energy efficiency. The second layer of glass further reduces UV transmission while maintaining high visible light transmittance, ensuring optimal natural lighting. The second air layer strengthens the overall thermal insulation and provides additional soundproofing. The third layer of glass acts as the final UV barrier, ensuring maximum UV blocking and safety. This structure combines the advantages of glass and air layers, offering comprehensive UV protection and environmental comfort solutions for buildings.

3.2. UV transmittance calculation

In this research, the wavelength range of sunlight is 300-2000nm, while the wavelength range of ultraviolet light is 300-400nm. This study simulates the solar spectrum in the range of 300-2000nm using Gaussian formula. FWHM is the width distributed at half of its maximum value, \( σ \) is the standard deviation, \( {λ_{0}} \) is the sunlight wavelength corresponding to the maximum light intensity, \( {I_{0}} \) is the maximum light intensity, and \( {L_{n}} \) is the thickness of the nth piece of glass.

The formula for calculating the transmittance of sunlight vertically incident on the nth layer of glass from the air is:

\( {T_{n}}=\frac{{I_{t}}}{{I_{i}}}=\frac{{(1-R)^{2}}}{{(1-R)^{2}}+4R{sin^{2}}(k{L_{n}})} \) (8)

Incident light formula:

\( σ=\frac{FWHM}{2\sqrt[]{2ln2}} \) (9)

\( {I_{i}}={I_{0}}*{e^{-\frac{{(λ-{λ_{0}})^{2}}}{2{σ^{2}}}}} \) (10)

The reflectivity formula of the two interfaces:

\( R={(\frac{n-{n_{0}}}{n+{n_{0}}})^{2}} \) (11)

The formula of Wave number:

\( k=\frac{2πn}{λ} \) (12)

The outgoing light is generated by the incident light passing through three layers of glass, and the outgoing light formula is:

\( {I_{t}}={I_{i}}*{T_{1}}*{T_{2}}*{T_{3}} \) (13)

The three-layer glass model is shown in Figure 1:

Figure 1. Three-layer glass model (Photo credit: Original).

\( {I_{t3}} \) in figure is the final transmitted light \( {I_{t}} \) passing through the three layers of glass mentioned above.

3.3. Fitness function

In the optimization of particle swarm optimization algorithm, the fitness function is the sum of light intensity through three layers of glass in 300-400nm, and the optimization objective is the minimum sum of ultraviolet light intensity through three layers of glass. This setting effectively ensures that the fitness function can well measure the ability of multi-layer glass models to resist ultraviolet rays.

4. Optimized Result

The refractive indices of glass and air in this study are 1.5 and 1.0, respectively. The maximum light intensity is set at 1000, and the FWHM is set at 500 nm. The wavelength of sunlight that corresponds to the maximum light intensity is roughly 580 nm.

The iterative connection between fitness and evolutionary algebra is shown in Figure 2:

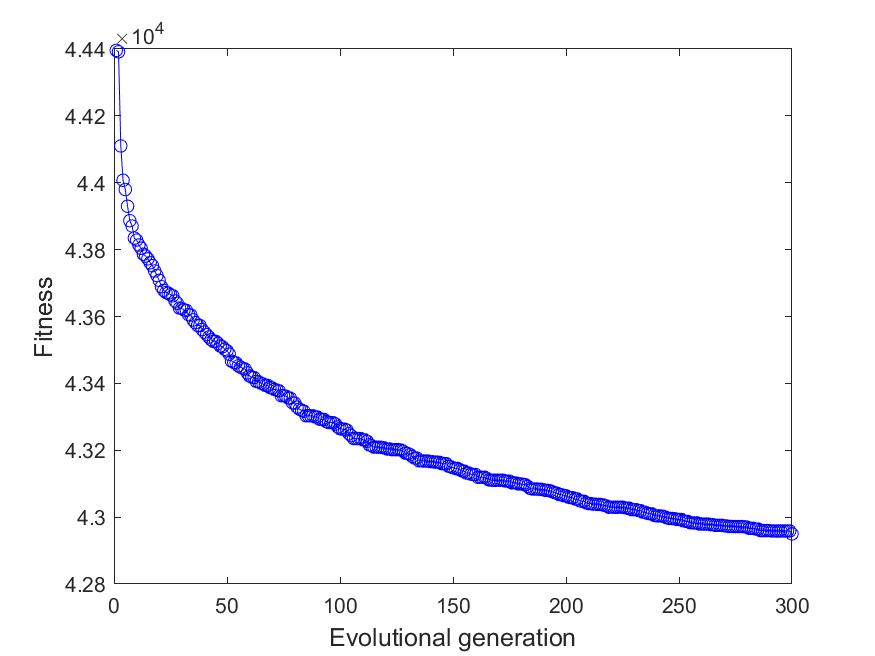
Figure 2. Iterative relationship between evolutionary algebra and fitness (Photo credit: Original).

Finally, the optimization results are obtained: L1 is 0.0069m, L2 is 0.0068m, L3 is 0.0075m, the optimal individual fitness within 300 generations, that is, the minimum sum of ultraviolet light intensity through the three layers of glass is 42244.7768, and the sum of incident ultraviolet light intensity is 55562.9581.

The relationship between the wavelength of sunlight and the transmitted light intensity through the three layers of glass is shown in Figure 3:

Figure 3. Relation between the wavelength of sunlight and the intensity of transmitted light passing through three layers of glass (Photo credit: Original).

The comparison between the transmitted light intensity and the incident light after the ultraviolet band passes through the three layers of glass is shown in Figure 4:

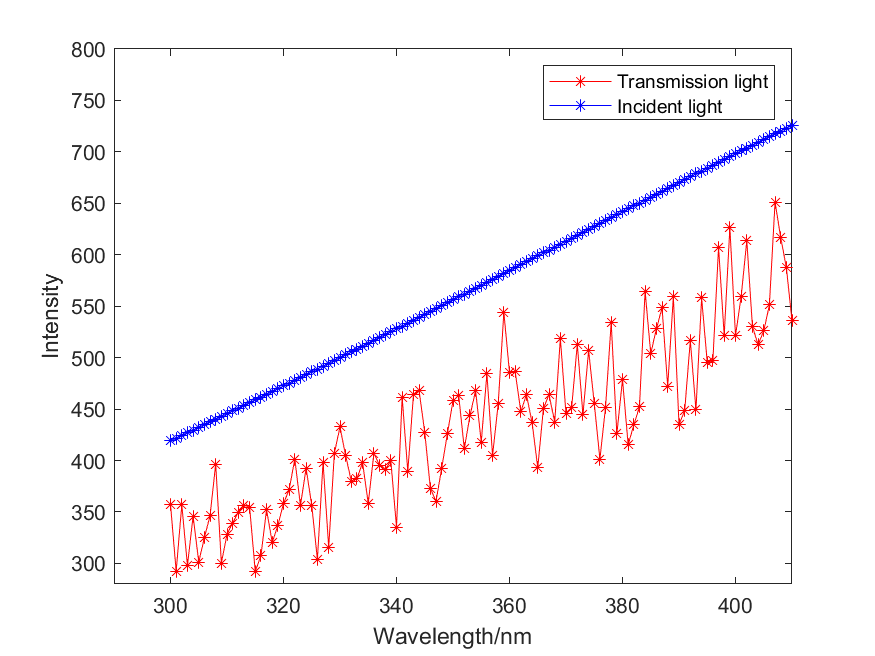
Figured 4. Comparison of transmitted light intensity and incident light after ultraviolet band passes through three layers of glass (Photo credit: Original).

5. Conclusion

This study successfully employed the particle swarm optimization technique to determine the optimal thicknesses for a three-layer window glass structure, aimed at minimizing ultraviolet transmission to enhance indoor human health protection. The optimization process yielded thicknesses of L1 = 0.0069m, L2 = 0.0068m, and L3 = 0.0075m, which effectively reduced the total ultraviolet light intensity passing through the glass to 42244.7768 from an initial intensity of 55562.9581. This significant reduction highlights the efficacy of the particle swarm optimization method in designing complex multilayer glass structures and underscores its potential as a practical solution for UV protection in window glass applications.

Several research avenues can further enhance the utility and applicability of multilayer glass designs. Future studies could explore the impact of various glass materials on UV blocking properties to identify the most effective combinations for UV protection. Additionally, considering the implications of climate change on glass performance, targeted optimizations could be conducted to adapt multilayer glass for different environmental conditions, thus enhancing its practical application across varying climates. Extending these optimization techniques to large-scale architectural projects could also provide valuable insights into their long-term practical and economic benefits. Such investigations will not only advance the field of multilayer glass design but also contribute significantly to safeguarding human health in built environments.