1. Introduction

By reading brain activity and turning it into control signals, a Brain-Computer Interface (BCI) represents an advanced technological approach, facilitating direct communication between the human brain and external devices, eliminating the need for peripheral nerves or muscles [1]. Visual stimuli with frequencies above 6 Hz provoke periodic electroencephalogram (EEG) responses that include both the fundamental and harmonic frequencies of the stimulus [2]. These particular reactions are called steady-state visual evoked potentials (SSVEPs). SSVEPs have been widely used in several domains, including as neuroengineering and clinical and cognitive neuroscience [3]. SSVEP-based BCI systems have garnered significant interest for research and practical use due to their high signal-to-noise ratio (SNR), swift information transfer rate (ITR), and user-friendliness requiring minimal training.

As Figure 1 illustrates, the SSVEP-BCI system is mainly made up of four parts: an EEG acquisition device, a control object, a signal processing module, and a visual stimulation source [4]. Similar to other HCI systems, SSVEP-BCI aims to maximize ITR by striking a compromise between signal duration and recognition accuracy. Machine learning (ML) and deep learning (DL) based approaches are the two categories into which previous research has divided feature extraction and classification algorithms.

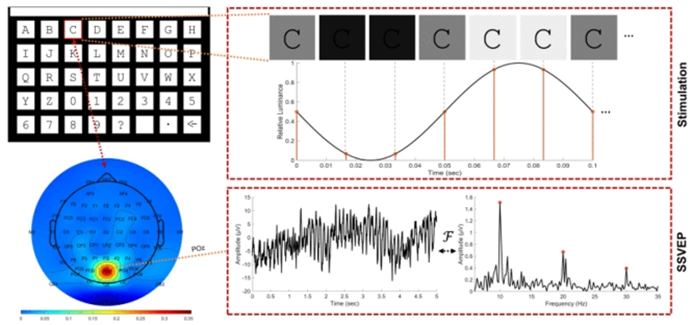
Figure 1. Principle of SSVEP-BCI system [4].

Many traditional machine learning approaches rely on manual feature selection and custom classifier design. One of the commonly used techniques in this area is Canonical Correlation Analysis (CCA) [5]. This method involves classifying SSVEPs by assessing the correlation of EEG signals with reference sinusoidal templates that match the stimulus frequencies. In an effort to enhance this method, Taejun et al. proposed Filter Bank Canonical Correlation Analysis with Dynamic Windows (FBCCA-DW), an adaptive method that optimizes classification by dynamically adjusting the window length of the temporal signal [6]. Their approach, when applied to a public dataset, achieved an Information Transfer Rate (ITR) of 146.81 bits per minute, utilizing only 1.53 seconds of EEG data for processing.

However, in the case of manual feature selection in machine learning techniques, the researcher's experience is paramount. Conversely, deep learning (DL) techniques have become increasingly prevalent in the BCI field, owing to their capacity to manage intricate nonlinear processes and autonomously derive features from raw EEG data [7]. The limitations of human feature selection are mitigated by DL models by the acquisition of multidimensional feature knowledge. Through the development of multidimensional feature knowledge, DL models are able to offset the limitations associated with human feature selection. For instance, Li et al.'s deep learning model Convolutional Correlation Analysis (Conv-CA) makes advantage of machine learning's notion of correlation coefficients [8]. This approach utilizes dual concurrent convolutional neural network (CNN) pathways to extract features from EEG and 3D reference signals, yielding superior outcomes. Following the computation of correlation coefficients among the features, a fully connected layer is employed to perform classification. Similar to this, Zhao et al. created a "filter bank CNN" that works incredibly well on publicly available datasets and illustrates the benefits of harmonic correlation on classification accuracy [9]. This is accomplished by employing filters from various frequency bands to gather correlation data between several harmonics. Moreover, the filter bank-based SSVEPformer (FB-SSVEPformer) by Chen et al. pioneered the use of the Transformer architecture for classifying SSVEPs [10].

This paper introduces the Filter Bank and Fourier Transform CNN (FBFCNN), a novel approach for SSVEP classification. The FBFCNN model feeds the real and imaginary components of the spectrum into a CNN, preprocesses SSVEP signals using filter banks, and uses an FFT approach to conduct time-frequency domain data changes. The proposed FBFCNN model outperforms other models in classification on SSVEP datasets.

2. Method

2.1. Baseline methods

Canonical Correlation Analysis (CCA). CCA is a traditional machine learning technique that is often employed in SSVEP-based BCIs to categorize SSVEPs [11]. In order to select two spatial filters that optimize the correlation between the SSVEP and template signals, CCA solves an optimization problem given SSVEP data and a template signal.

\( ρ(X,Y)=\underset{{w_{x}},{w_{y}}}{max}{\frac{E[w_{x}^{T}X{Y^{T}}{w_{y}}]}{\sqrt[]{E[w_{x}^{T}X{X^{T}}{w_{y}}]E[w_{y}^{T}Y{Y^{T}}{w_{y}}]}}} \) (1)

, where \( ρ(X,Y) \) stands for \( X \) and \( Y \) ’s maximal canonical correlation.

2.1.1. Complex Convolutional Neural Network (C-CNN). 2020 saw the proposal of the CNN model known as C-CNN by Ravi et al. It has two hidden layers. Its input is the complex spectrum of data that has been FFT-transformed, and it goes through two convolutional layers. Research has shown that C-CNN outperforms other standard methods [12].

2.1.2. Filter Bank Convolutional Neural Network (FBCNN). Prior studies have demonstrated that integrating filter banks with deep learning or machine learning models can significantly improve the efficacy of SSVEP classification [13]. The C-CNN model achieved robust performance in SSVEP classification tasks, indicating that the complex spectrum derived from FFT analysis provides superior outcomes compared to the magnitude spectrum alone.

2.2. FBFCNN model

Figure 2 illustrates the two principal components of the FBFCNN model introduced in this research: a convolutional neural network (CNN) that processes the complex frequency spectrum obtained from FFT-transformed data, and a filter bank that pre-processes the SSVEP input by applying multiple filters to segment the signal.

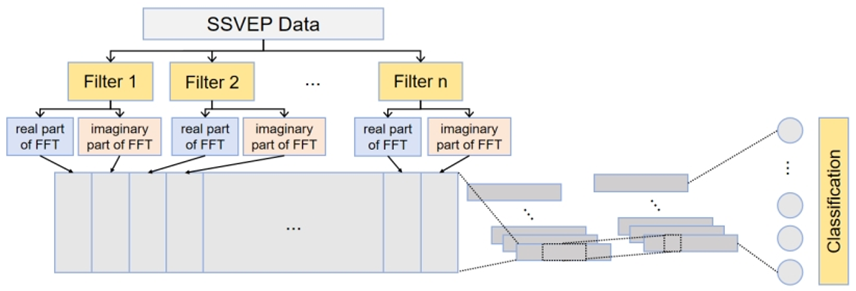
Figure 2. Architecture of FBFCNN model (Figure Credits: Original).

The filter bank consists of N filters, each of which has a distinct zero-phase IIR filter passband. With the use of this filter bank, SSVEP data can be divided into several sub-band components for independent investigation of the data's harmonic content. These components can then be combined to improve classification accuracy.

The stimulation bandwidth is ≤ 8 Hz for the majority of SSVEP BCI systems, including the publicly available datasets used in this research. The filter bank's passbands begin at n × 8 Hz and go up to 88 Hz, where maximum performance is attained when n ∈ [1, 2,..., n] [14]. The FBFCNN model's filter bank architecture is consistent with Chen's research. Following the filtering procedure, the data is Fourier transformed, and the real and imaginary components are handled independently for additional examination.

In the complex spectrum convolutional neural network, two convolutional layers precede a fully connected layer. Large kernels with a stride of 1 are used in the first convolutional layer to extract FFT features from each channel and combine them into a new feature set for additional processing. Batch normalization is used to accelerate training and enhance model stability. The rate of dropout is set at 0.5 to prevent overfitting. Using smaller kernels with a larger stride, the second convolutional layer compresses the length of the input and extracts local attributes. Every component from the levels before it is connected to N neurons in the last completely connected layer, each of which represents a target class.

3. Results

3.1. Dataset and preprocessing

Using the Nakanishi dataset, this study assessed the performance of the suggested FBFCNN algorithm [15]. This dataset comprises SSVEP data from 10 healthy participants with either normal vision or vision that has been corrected to normal. Twelve flashing visual stimuli at various frequencies (f0 =9.25 Hz, Δf = 0.5 Hz) and phases (Ø0=0, ΔØ = 0.5π) were shown to each individual. Eight electrodes were used to gather the SSVEP data, with a sampling rate of 2048 Hz. Every participant finished 15 blocks of the experiment, in which they had to gaze at a randomly selected visual stimulus for four seconds, as determined by the stimulus program. Each participant completed 12 trials total, covering all 12 goals. Subsequently, an infinite impulse response filter was used to downsample all data epochs to 256 Hz after band-pass filtering them from 6 Hz to 80 Hz.

3.2. Training details

The training loss for the target recognition task was determined using the negative log-likelihood loss function (NLLoss) [16]. Assuming that each parameter is represented by, the total loss was estimated as follows:

\( Loss(θ)=\frac{1}{Ω}\sum _{i=1}^{Ω}NLLoss(O_{i}^{j}-\overline{O}_{i}^{j}) \) (2)

, where Ω denotes the number of trials, \( O_{i}^{j} \) is the prediction result for the i-th trial, and \( \overline{O}_{i}^{j} \) represents the input data for the j-th subject. The model parameters were optimized using the Adam optimizer, configured with a batch size of 512 and a learning rate of 0.01 [17]. Training was performed over 600 epochs, with early stopping applied to halt the process if the validation loss failed to improve after 30 consecutive epochs.

3.3. Quantitative performance

3.3.1. Accuracy. Accuracy is defined as the proportion of correctly identified samples relative to the overall test sample count. As indicated in Table 1, this study evaluated the FBFCNN model's accuracy across a range of participants in comparison to other benchmarks including CCA, C-CNN, and FBtCNN. The findings show that for SSVEP data, the FBFCNN model achieves a smaller standard deviation and higher classification accuracy.

Table 1. Performance on different subjects.

3.3.2. Information transfer rate. Sophisticated signal processing and machine learning techniques are necessary for signal decoding—the process of removing pertinent information from EEG data—in order to guarantee that BCI devices function as intended. Accuracy and Information Transfer Rate (ITR) are two important measures that are frequently used to evaluate the performance of a BCI system based on SSVEP. The probability of accurately detecting the target stimulus is represented by accuracy, and the quantity of information supplied by the BCI system within a specific time frame is measured by ITR. The formula below is used to compute the ITR [18]:

\( ITR=\frac{60}{T}({log_{2}}{N}+P{log_{2}}{P}+(1-P){log_{2}}{[\frac{1-P}{N-1}]}) \) (3)

, where T represents the mean time needed to issue a command, P denotes the accuracy, and N signifies the number of targets.

The ITR performance of FBFCNN was compared to CCA, C-CNN, and FBtCNN across various subjects, as shown in Figure 3.

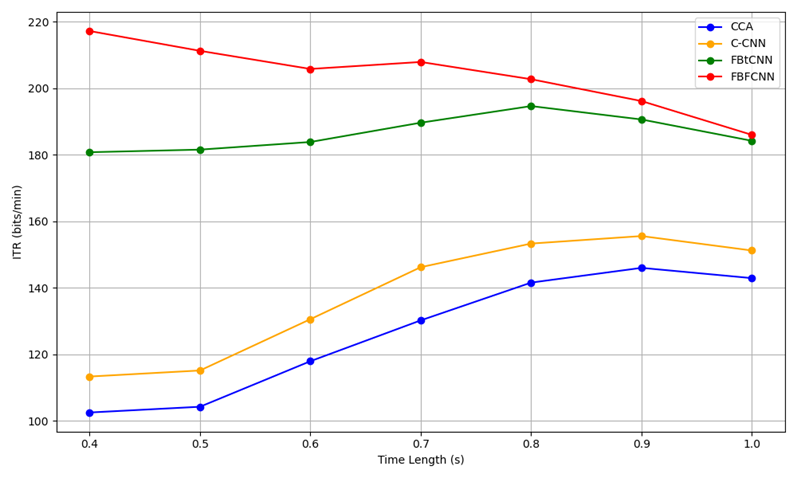
Figure 3. ITR performance over time (Figure Credits: Original).

The ITR data plot shows that the FBFCNN can classify SSVEP signals with high accuracy in a short time, achieving higher communication efficiency.

3.3.3. Confusion matrices. An important technique for assessing how well categorization models work is a confusion matrix. With each row denoting an actual class and each column denoting a predicted class, the table contrasts expected and actual results. Accuracy, precision, and recall are just a few of the performance metrics that can be computed by examining the data in a confusion matrix. These metrics are essential for determining how successful a model is.

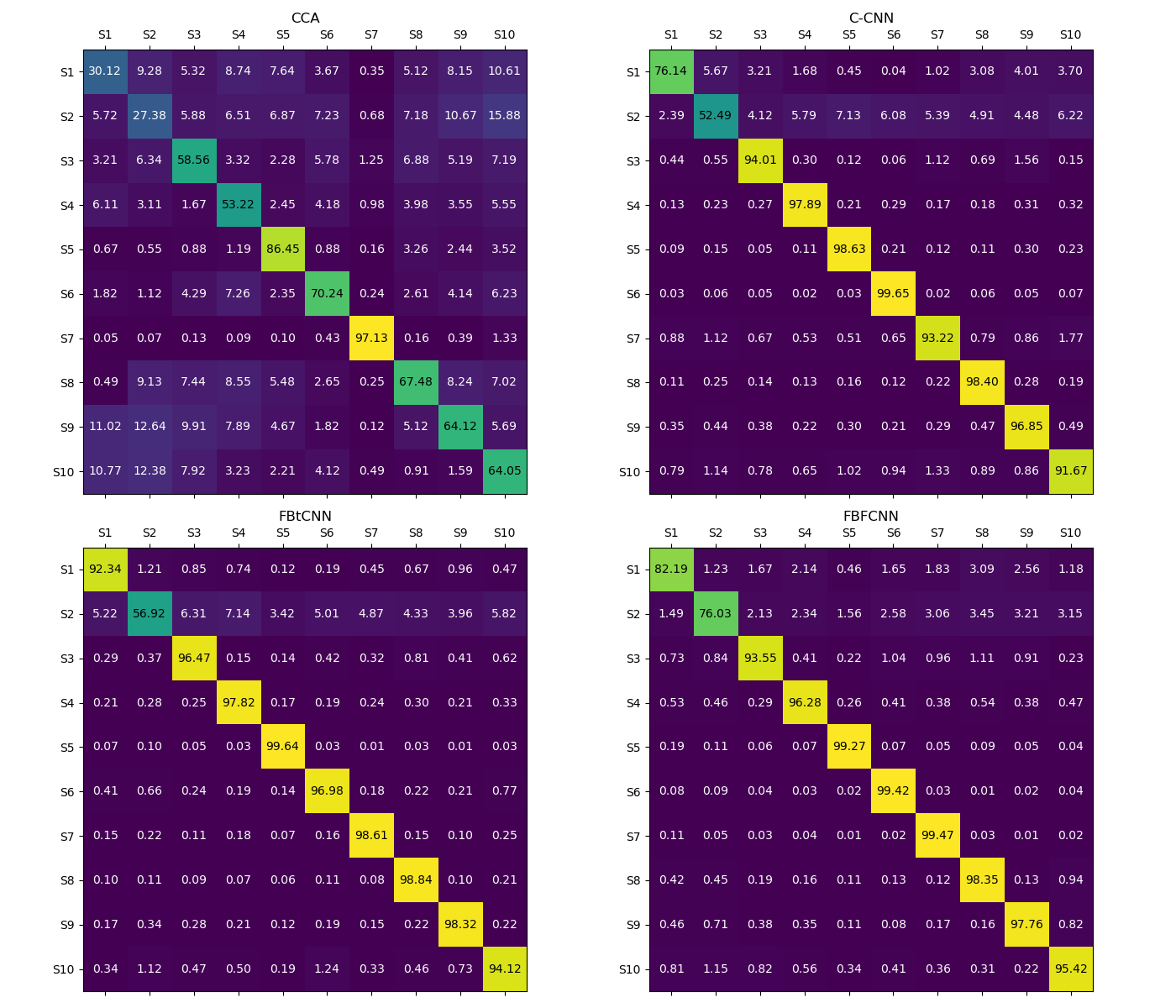
Figure 4. Performance of confusion matrices (Figure Credits: Original).

From the confusion matrix in Figure 4, it can be seen that FBFCNN has a higher accuracy and a lower recall.

4. Discussion

Although the FBFCNN model shows promising results in classifying SSVEPs, it has some limitations that should be addressed. First, the model's complexity can result in higher computational costs, making it less practical for real-time use on devices with limited resources. Future research could focus on optimization methods like pruning or quantization to lower computational demands without compromising accuracy. Additionally, the model has been trained and validated on specific datasets, and its ability to generalize to other EEG signal types or alternative BCI paradigms is yet to be confirmed. Broadening the testing scope to encompass a more diverse array of datasets and EEG signals may provide a more comprehensive evaluation of the model's performance.

In addition to overcoming the existing limitations, future studies could explore the integration of more sophisticated neural network architectures to enhance the model's ability to detect intricate temporal and spatial patterns within EEG signals. Additionally, integrating domain adaptation techniques could enhance the model's robustness across varying subjects and recording conditions, making it more adaptable for use in real-world BCI systems. This would further increase its practical utility by ensuring consistent performance in diverse environments and user scenarios.

5. Conclusion

The author of this work suggested a brand-new method for categorizing SSVEPs in BCI systems: the FBFCNN. The FBFCNN model employs the Fourier Transform to convert EEG signals into the frequency domain, where real and imaginary components are captured for input into a CNN. This procedure begins with preprocessing the data using a filter bank. Based on public SSVEP datasets, the results demonstrate that the FBFCNN works better than conventional approaches, obtaining greater accuracy and ITR. These results demonstrate FBFCNN's promise as a reliable and effective technique for brain signal decoding in real-time for BCI applications. Subsequent research endeavors will center on refining the model to minimize computing expenses, examining its applicability to diverse EEG datasets, and incorporating supplementary neural network structures to amplify its efficacy. In order to advance SSVEP-based BCIs and create more efficient and user-friendly devices, the FBFCNN model offers a viable path.