1. Introduction

Electrocardiogram (ECG) is a crucial diagnostic tool for heart diseases, recording the heart’s electrical activity to detect abnormalities like arrhythmias and myocardial ischemia, emphasizing its clinical importance. [1]. With technological advancements, automated ECG analysis has become a research focus in cardiology. However, there remains room for improvement in both accuracy and robustness [2].

Previous studies, such as the work of Avinash L. Golande and T. Pavankumar, have introduced CNN and LSTM-based approaches for automated ECG classification. While these methods perform well in most scenarios, they still struggle with noise robustness [3]. Another study employed LSTM for ECG signal analysis, effectively capturing the temporal features in ECG data. However, due to its high computational complexity and sensitivity to long-term dependencies, this approach leads to increased computational costs [4].

This paper presents a novel approach using SNN to address the aforementioned challenges. The method merges CNN with LIF spiking neurons to enhance noise handling and improve classification performance in ECG signals. The following sections include a flowchart of the proposed method and a diagram of the neural network architecture, illustrating the design and structure.

The method’s design is based on a deep learning framework, particularly integrating CNN with SNN. The architecture combines convolutional layers and LIF spiking neurons to enhance feature extraction and classification performance for ECG signals. Adaptive learning rates and regularization strategies are employed to ensure robustness and efficiency when handling large-scale ECG data.

This study's main contributions can be summarized as below: (1) A novel SNN-based framework, SNN Net, is proposed for ECG anomaly detection, which effectively addresses the noise issue in ECG signals during the data preprocessing stage using wavelet transform. (2) SNN Net achieves a test accuracy of 97.98% on the MIT-BIH Arrhythmia Dataset, outperforming traditional LSTM architectures.

2. ECG Signal Preprocessing

The preprocessing of ECG signals is a crucial step in ensuring accurate diagnosis. One of the most effective methods for denoising ECG signals is the application of wavelet transform. This chapter will introduce the Application of Wavelet Transform and Denoising as well as how to process ECG datasets.

2.1. Dataset Attributes: Analysis of the MIT-BIH Arrhythmia Dataset

Widely utilized for ECG-based arrhythmia detection, the MIT-BIH Arrhythmia Dataset consists of 48 recordings from 47 individuals, captured using two leads at a sampling rate of 360 Hz. Derived from Lead II and Lead V1, the recordings have a 360 Hz sampling rate and are digitized at 11-bit resolution. Each record is manually annotated by cardiologists, identifying the R-peaks and various arrhythmia types. The dataset includes 15 different arrhythmia categories, with common types such as premature ventricular contraction (PVC), right bundle branch block (RBBB), left bundle branch block (LBBB), atrial premature contraction (APC), normal beats (N). Each record consists of approximately 108,000 data points. Pre-processing and data augmentation are often necessary due to the imbalance in arrhythmia classes. The dataset is extensively used in deep learning applications and machine learning for arrhythmia classification and ECG signal analysis. [5].

2.2. Application of Wavelet Transform and Denoising

Wavelet transform is highly effective in separating cardiac signals from noise. This method applies thresholding to attenuate noise, improving ECG signal quality and ensuring accurate analysis of cardiac dynamics. [6,7].In the proposed framework, The denoising process uses wavelet thresholding to remove noise while preserving the waveform's morphological characteristics. [7]. This preparatory step is crucial for ensuring that the ECG signals used in further analysis are as clean and accurate as possible, thereby improving the reliability of the diagnostic outcomes.

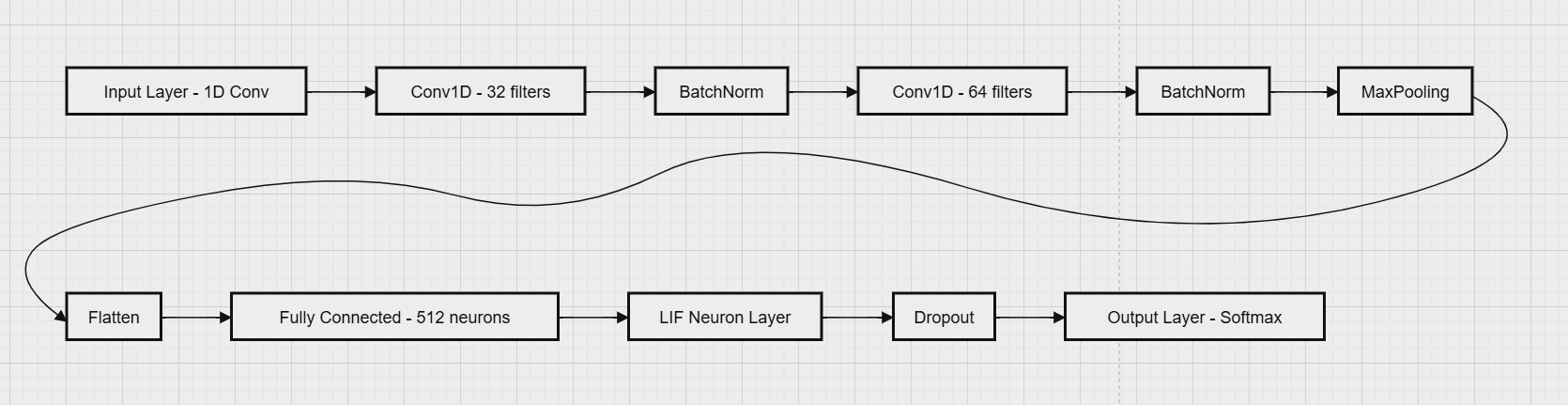
Figure 1. Flowchart of the Proposed Method (Insert Flowchart)

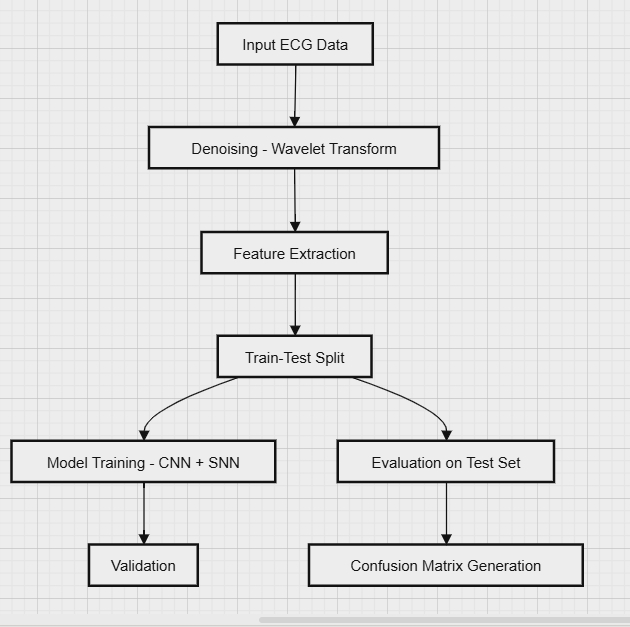
Figure 2. Network Architecture Diagram (Insert Architecture Diagram)

2.3. Dataset Processing and Feature Extraction

Processing ECG datasets is vital to ensure the accuracy and representativeness of cardiac activity in subsequent analyses. Given that ECG signals are often noisy and irregular, careful preprocessing is required to extract meaningful features for classification. The segmentation of ECG signals is particularly important as it allows for the identification of individual heartbeats within a continuous recording. These features often include temporal and morphological characteristics of the ECG waveform, which are essential for accurate diagnosis [8]. The use of time-frequency analysis methods, such as wavelet transform, can also enhance feature extraction by providing a more detailed representation of the signal's frequency content. Figure 3 illustrates the segmented heartbeats as depicted by Python.

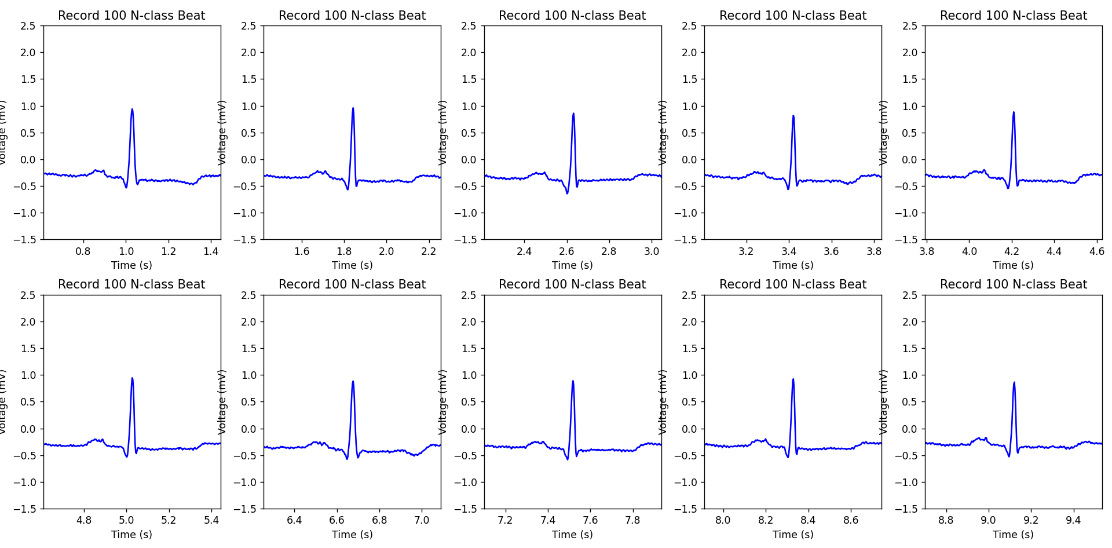
Figure 3. Segmented heartbeats from N and V classes in the MIT-BIH Arrhythmia dataset

3. Application and Limitations of the LSTM Model

3.1. LSTM Model Architecture Design

The architecture features two bidirectional LSTM layers, each with 64 hidden units, designed to capture both short- and long-term dependencies in ECG signals. The first layer, with return sequences enabled, processes immediate temporal dependencies in both directions. [9].

In each LSTM cell, the input gate controls the influence of the current input \( x_t \) and the previous hidden state \( h_{t - 1} \) ​ on the cell state:

\( i_t=\sigma(W_i\bullet \left[h_{t - 1},x_t\right]+b_i) \) (1a)

The forget gate regulates how much of the previous cell state \( C_{t - 1} \) ​ is retained:

\( f_t=\sigma(W_f\bullet \left[h_{t - 1},x_t\right]+b_f) \) (1b)

Next, a candidate cell state \( \overline{c_t}​ \) ​ is calculated to generate the new cell state:

\( \overline{c_t}=\ \tanh{(W_C\bullet \left[h_{t - 1},x_t\right]+b_C)} \) (1c)

The updated cell state \( C_t \) ​ is a combination of \( C_{t - 1} \) and the candidate cell state, modulated by the forget and input gates.:

\( C_t=\ f_t\ast C_{t - 1}+i_t\ast \overline{c_t} \) (1d)

Finally, The output gate determines how much of \( C_t \) is transferred to the hidden state \( h_t \) ​:

\( o_t=\sigma(W_o\bullet \left[h_{t - 1},x_t\right]+b_o) \) (1e)

\( h_t \) ​ is the LSTM cell's output, combining the output gate with the current cell state:

\( h_t=\ o_t\ast \tanh(C_t) \) (1f)

The second LSTM layer continues this bidirectional processing to identify and capture longer-term trends within the signal. Following the LSTM layers, a fully connected Dense layer with a softmax activation function is applied, which maps the processed data to the final output [10]. This architecture is particularly well-suited for classifying various types of cardiac events, such as arrhythmias, by leveraging the temporal information contained in the ECG signals. The framework is illustrated in Figure 4.

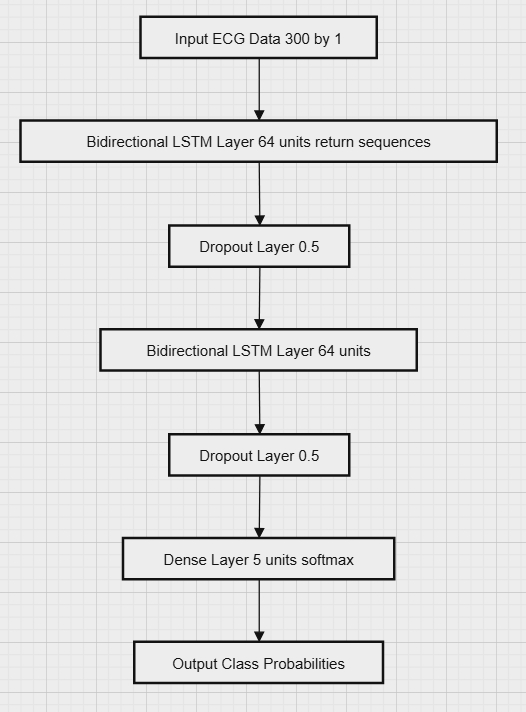
Figure 4. Architecture of the LSTM Model Used for ECG Signal Classification

3.2. Performance of LSTM in ECG Signal Classification

The LSTM model was trained for 10 epochs with a batch size of 16, using two bidirectional LSTM layers and a softmax layer to classify ECG signals into five categories. It achieved 93.47% training accuracy, 94.36% validation accuracy, 94.65% test accuracy, and a test loss of 0.1786. Despite high accuracy, the model struggled with specific arrhythmias.

Table 1. Training and Validation Performance of LSTM Model on ECG Signal Classification

4. Introduction of the SNN Model

4.1. Structure and Design of the SNN Model

The architecture in our study integrates CNN with SNN [11]. The framework is illustrated in Figure 1. The CNN layers extract spatial features from the ECG data, preparing it for the SNN layers, which consist of LIF neurons. The LIF model has been identified through research as a capable spiking neural model for describing a range of biological phenomena. [12]. As computational units, LIF neurons can simulate both Turing machines and traditional sigmoidal networks, representing signals through delta functions[15], where inputs and outputs are written as

\( x(t)=\sum _{j=1}^{n}{\delta(t\ - {\ \tau}_j\ )}\ \) for spike times \( {\ \tau}_j \) (2a)

Each unit carries out a limited range of fundamental operations—such as delaying, weighting, spatial summation, temporal integration, and thresholding—integrated into a unified system capable of performing various computational tasks, such as binary classification, adaptive feedback, and temporal logic. Figure 7(a) illustrates the standard LIF neuron model [13]. This neuron model has the following component: (1) \( N\ \) inputs, representing induced currents in the input synapses xj(t)x_j(t)xj​(t), where each input is a continuous time series that may consist of spikes or continuous analog signals; (2) an internal membrane potential \( V_m(t) \) ; (3) a single output state \( y(t) \) . [14]

Each input is weighted independently by \( \omega_j \) , which can be positive or negative, and delayed by \( \tau_j \) , producing a time-shifted input signal[14]. These inputs are then summed spatially (pointwise), producing an aggregate input. This aggregate input generates an applied current between adjacent neurons, which can be represented as:

\[ I_{app}​(t)=\sum _{j=1}^{N} ω_{j}​x_{j}​(t - τ_{j}​)​ \] ​ (2b)

In this model, the input signals are processed by applying weights and time delays, and then summed to form the applied current \( I_{app}(t) \) . This current passes through an integrator, and then through an activation function module, generating the output \( y(t) \) . Once the neuron's membrane potential hits the threshold, it triggers an output and the system is subsequently reset.

The dynamics of the network are influenced by the weights \( \omega_j \) and delays \( \tau_j \) , enabling the programming of a neuromorphic system. The behavior of individual neurons is determined by internal parameters, such as the resting potential \( V_L \) and the membrane time constant \( \tau_m \) . The membrane potential \( V_m(t) \) is affected by three factors: passive current leakage, active current pumping, and external inputs that cause changes in membrane conductance over time. By incorporating a set of digital conditions, the standard LIF model for a single neuron can be derived:

\[ \frac{dV_m(t)}{dt}=\frac{V_{L}​}{τ_{m}} - \frac{V_{m}(t)}{τ_{m}}+ \frac{1}{C_{m}}I_{app}(t) \] (2c)

In this equation, \( \frac{dV_m(t)}{dt}\ \) represents activation, \( \frac{V_{L}​}{τ_{m}} \) represents active pumping, \( \frac{V_m\left(t\right)}{\tau_m} \) represents leakage, \( \frac{1}{C_m}I_{app}\left(t\right) \) represents external inputs.

If \( V_m\left(t\right)\ \text{>}\ V_{thresh} \) , then release a pulse at \( t_f \) and set \( V_m\left(t\right)\ \rightarrow \ V_{reset} \)

The behavior of an LIF neuron, as illustrated in Figure 7(b). When the membrane potential \( V_m(t) \) reaches or exceeds the threshold \( V_{thresh} \) ​, the neuron generates a spike, represented as \( \ y\left(t\right)=\ \delta(t - t_f) \) ,with \( t_f \) being the time of spike firing, and \( V_m\left(t\right) \) is reset to \( V_{thresh} \) . A refractory period follows, during which \( V_m\left(t\right) \) slowly returns to the resting potential \( V_L \) , making it more difficult, though not impossible, to fire another spike. As a result, the output of the neuron is a continuous spike series, expressed as \( y\left(t\right)=\ \sum _{i}{\delta(t - t_i)} \) , where \( \ t_i \) represents the spike times. [14]

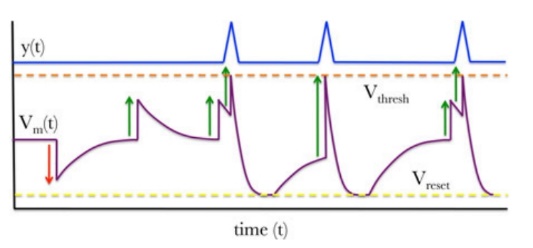
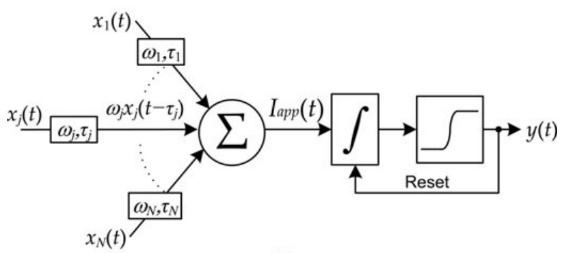
Figure 6. (a) The leaky integrate-and-fire neuron functional description. (b) A depiction of spiking dynamics in an LIF neuron.

4.2. Performance of SNN in ECG Signal Classification

The SNN model underwent training for 10 epochs with a batch size of 16, achieving 99.39% training accuracy, 99.17% validation accuracy, and 97.98% test accuracy, with a test loss of 0.0932. Using Leaky Integrate-and-Fire neurons, the SNN outperformed the LSTM model in handling ECG signal timing patterns, though its higher computational complexity may affect real-time performance.

Table 2. Training and Validation Performance of SNN Model on ECG Signal Classification

5. Results

5.1. Comparison of Classification Accuracy and Loss

The comparison between the LSTM model before optimization and the SNN model after optimization shows clear improvements in both accuracy and loss. The LSTM model recorded a test accuracy of 94.65% and a test loss of 0.1786, whereas the optimized SNN model exceeded this with a test accuracy of 97.98% and a significantly reduced test loss of 0.0932. These findings demonstrate the SNN model's superior capability to capture both spatial and temporal patterns in ECG data, resulting in more accurate classifications.

5.2. Comparison of Confusion Matrices

The confusion matrices further illustrate the performance improvements after optimization which is shown in Figure 9 and Figure 10. The optimized SNN model not only facilitated higher accuracy and lower loss but also demonstrated enhanced capability in distinguishing between ECG signal categories, especially in noisy or complex cases. This comparison underscores the effectiveness of the optimization in improving model performance for ECG signal classification.

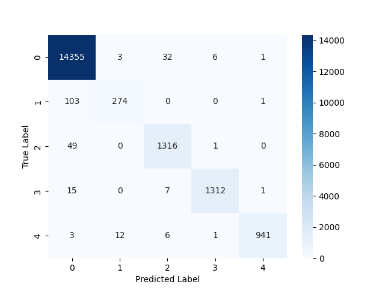
Figure 7. LSTM Model Confusion Matrix for ECG Signal Classification

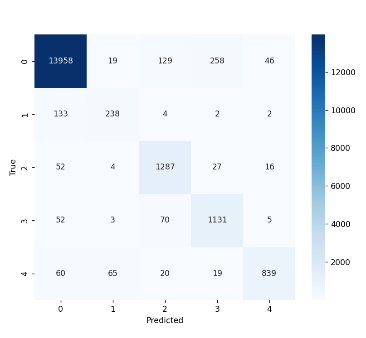
Figure 8. SNN Model Confusion Matrix for ECG Signal Classification

6. Conclusion

Two ECG classification models –LSTM and SNN—were developed and evaluated in this study. Both performed well, with the LSTM excelling in capturing temporal dependencies but requiring more computational resources. The SNN, being more resource-efficient and biologically inspired, is suitable for low-power applications like embedded systems, though it slightly lags in accuracy due to complex feature extraction. While LSTM currently outperforms SNN, future research should optimize SNN architectures, explore hybrid models, improve training algorithms, and investigate neuromorphic hardware and transfer learning for better generalization.