1. Introduction

The Knuth-Morris-Pratt (KMP) algorithm, developed by Donald Knuth, Vaughan Pratt, and James Morris in 1977, is a widely used string matching algorithm.[1] It efficiently searches for patterns within text by using a "Partial Match Table" (or "Suffix Array") to skip unnecessary comparisons, thereby reducing overall time complexity. A key advantage of the KMP algorithm is its ability to quickly move past matched characters, in contrast to the naive approach

There exist various implementations of the KMP algorithm that differ in terms of space complexity, time complexity, and execution efficiency. Recently, there has been a growing interest in comparing these implementations to understand the trade-offs and identify the most efficient one for specific applications. This paper aims to evaluate different implementations based on time complexity (the number of operations performed), space complexity (memory usage), and execution efficiency (real-world performance influenced by factors like hardware and compiler optimization). By comparing these implementations, practitioners can select the most appropriate version for their needs while considering constraints like memory and processing power. The study compares three KMP implementations: a classic version, an improved version using nextval array, and an improved version using hybrid BM and KMP algorithm.[2] The evaluation is based on time complexity, space complexity, and execution efficiency. However, the study is limited to widely available implementations and specific test cases, which may not generalize to all scenarios.

2. Literature Review

2.1. The Original KMP Algorithm

The Knuth-Morris-Pratt (KMP) algorithm, introduced by Knuth, Pratt, and Morris in 1977, is the first linear-time string matching algorithm with a time complexity of O(m + n)[3]. It operates by constructing a "Failure Table" (or Partial Match Table) that records the longest common prefix and suffix in substrings of the pattern. This table enables the KMP algorithm to skip unnecessary comparisons, thereby reducing the number of steps required for pattern matching. Instead of restarting comparisons after a mismatch occurs, the KMP algorithm shifts the pattern by a calculated amount based on the Failure Table, enhancing efficiency when compared to naive string matching techniques.

2.2. Optimizations of the KMP Algorithm

Several optimizations have been developed to enhance the performance of the KMP algorithm[4-9]. One common improvement involves creating a "next array" by shifting the values of the Failure Table, simplifying programming logic. The Boyer-Moore (BM) Algorithm, introduced in 1977, improves upon KMP by comparing characters from right to left and using the "bad character" and "good suffix" rules to maximize shifts after mismatches, making it more efficient in practice.

The Sunday Algorithm is another fast string matching technique that focuses on skipping characters during mismatches using an approach similar toBM algorithm. However, its worst-case time complexity is O(mn), which makes it less efficient in some scenarios. Additionally, the Shift-Add Approach combines KMP and finite automata concepts to improve performance, though it requires more memory for larger patterns.

2.3. KMP Algorithm in Specialized Applications

Further optimizations to KMP have been proposed for specific applications. The eKMP Algorithm improves KMP’s efficiency for DNA sequence matching by dynamically adjusting the search window. [10]This demonstrates KMP's flexibility in areas beyond text matching, such as bioinformatics.

The Rabin-Karp Algorithm, introduced in 1987, uses hashing for pattern matching and is effective for multidimensional problems. Combining KMP with Rabin-Karp has led to hybrid algorithms that solve two-dimensional string matching more efficiently.

2.4. Summary

The KMP algorithm has been widely studied and optimized, with alternatives like Boyer-Moore and hybrid approaches offering improved efficiency in specific contexts. These advancements highlight the importance and adaptability of KMP across various domains, from text searching to bioinformatics.

3. Methodology

3.1. Experimental Setup

In this section, the experimental setup used to evaluate and compare the performance of different KMP algorithm implementations is described. The goal is to measure the execution time and memory usage across four KMP algorithm variants using Python. The four implementations evaluated in this experiment are as follows: Basic KMP Algorithm, which is the standard KMP algorithm and uses an array to store the partial matches (prefix function); KMP with nextval Optimization, an optimized version of the KMP algorithm that reduces redundant comparisons during pattern matching by tweaking the prefix function; Boyer-Moore Algorithm (BM), an alternative string-matching algorithm that utilizes heuristics (e.g., bad character rule) to shift the pattern more efficiently after mismatches; and Hybrid KMP-BM Algorithm, a hybrid approach that uses Boyer-Moore for longer patterns and KMP for shorter ones to take advantage of both algorithms' strengths. Each implementation was tested using Python, and a set of predefined test cases was used to compare their performance. The performance was measured in two key areas: Execution time, which is how quickly each algorithm processes the text to find occurrences of the pattern, and Memory usage, which is the peak memory consumption during the execution of each algorithm.

3.2. Selection of Code Implementations

In this study, we implemented four different variations of the KMP algorithm to analyze and compare their performance. Each implementation was carefully designed and written in Python to maintain consistency across the experiment. The four methods chosen were:

3.2.1. Basic KMP Algorithm

This is the traditional implementation of the KMP algorithm, which uses a prefix function to avoid redundant comparisons when searching for a pattern in a given text. The following code demonstrates the basic KMP search function:

def compute_prefix_function(self):

        m = len(self.pattern)

        prefix = [0] * m

        k = 0  # the length of the longest prefix suffix

        for q in range(1, m):

            while k > 0 and self.pattern[k] != self.pattern[q]:

                k = prefix[k - 1]

            if self.pattern[k] == self.pattern[q]:

                k += 1

            prefix[q] = k

        return prefix

    def kmp_search(self):

        n = len(self.text)

        m = len(self.pattern)

        prefix = self.compute_prefix_function()  # Preprocess the pattern

        q = 0  # number of characters matched

        matches = []  # list to store the starting indices of matches

        for i in range(n):

            while q > 0 and self.pattern[q] != self.text[i]:

                q = prefix[q - 1]  # Next character does not match

            if self.pattern[q] == self.text[i]:

                q += 1  # Next character matches

            if q == m:

                matches.append(i - m + 1)  # Pattern found; append its starting index

                q = prefix[q - 1]  # Look for the next possible match

        return matches

3.2.1.1.

KMP with nextval Optimization

This variant improves upon the basic KMP algorithm by using the nextval array, which reduces redundant comparisons during pattern matching. The code below illustrates the kmp_search_nextval function:

def compute_nextval(self):

        m = len(self.pattern)

        nextval = [0] * m

        k = 0  # the length of the longest prefix suffix

        for q in range(1, m):

            while k > 0 and self.pattern[k] != self.pattern[q]:

                k = nextval[k - 1]

            if self.pattern[k] == self.pattern[q]:

                k += 1

            if self.pattern[q + 1] != self.pattern[k] if q + 1 < m else True:

                nextval[q] = k

            else:

                nextval[q] = nextval[k - 1] if k > 0 else 0

        return nextval

    def kmp_search_nextval(self):

        n = len(self.text)

        m = len(self.pattern)

        nextval = self.compute_nextval()  # Preprocess the pattern with nextval optimization

        q = 0  # number of characters matched

        matches = []  # list to store the starting indices of matches

        for i in range(n):

            while q > 0 and self.pattern[q] != self.text[i]:

                q = nextval[q - 1]  # Use nextval to skip redundant comparisons

            if self.pattern[q] == self.text[i]:

                q += 1  # Next character matches

            if q == m:

                matches.append(i - m + 1)  # Pattern found; append its starting index

                q = nextval[q - 1]  # Look for the next possible match

        return matches

3.2.1.2.

Boyer-Moore Algorithm (BM)

This algorithm employs two heuristics—the bad character rule and the good suffix rule—to improve the efficiency of pattern matching. It shifts the pattern more significantly than KMP when mismatches occur. Below is the code for the Boyer-Moore search:

def bad_character_heuristic(self):

        """Generate the bad character heuristic table for the BM algorithm."""

        bad_char = [-1] * 256  # Assuming ASCII character set

        for i in range(len(self.pattern)):

            bad_char[ord(self.pattern[i])] = i

        return bad_char

    def bm_search(self):

        """Boyer-Moore string search algorithm."""

        m = len(self.pattern)

        n = len(self.text)

        bad_char = self.bad_character_heuristic()

        s = 0  # shift of the pattern with respect to text

        matches = []

        while s <= n - m:

            j = m - 1

            # Decrease index j of pattern while characters are matching

            while j >= 0 and self.pattern[j] == self.text[s + j]:

                j -= 1

            # If the pattern is present at current shift, append the index

            if j < 0:

                matches.append(s)

                s += (m - bad_char[ord(self.text[s + m])] if s + m < n else 1)

            else:

                # Shift the pattern to align the bad character in text with its last occurrence in pattern

                s += max(1, j - bad_char[ord(self.text[s + j])])

        return matches

3.2.1.3.

Hybrid KMP-BM Algorithm

This approach combines both KMP and Boyer-Moore algorithms. For shorter patterns, it uses the basic KMP algorithm, while for longer patterns, it leverages the Boyer-Moore algorithm. The hybrid search method is implemented as follows:

def hybrid_kmp_bm_search(self):

        """Hybrid approach using BM for longer patterns and KMP for shorter ones."""

        if len(self.pattern) > 10:

            return self.bm_search()

        else:

            return self.kmp_search()

3.3. Performance Evaluation Metrics

To evaluate the performance of the selected algorithms, we employed the following metrics: Execution Time, which measures the average time taken for each algorithm to search for a pattern in a given text. Time was measured using Python’s timeit module, and the average execution time was calculated over 10 runs to ensure accuracy. Additionally, Memory Usage was measured using the memory_profiler package in Python, which tracks the memory consumption during execution.

3.4. Experimental Procedure

The experimental setup was designed to run each algorithm on different combinations of text and pattern lengths. Test cases were defined with text lengths of 10,000, 50,000, and 100,000 characters, and pattern lengths of 5, 50, and 500 characters. For each test case, random strings of alphanumeric characters were generated for both the text and pattern, enabling testing of each algorithm's performance in a realistic and varied set of conditions. The same randomly generated text and pattern combinations were used across all algorithms to ensure fairness. The experiment followed this procedure: first, for each text and pattern length combination, the four algorithm implementations were tested. Second, execution time was measured by running each algorithm 10 times, and the average time was recorded. Third, peak memory usage was tracked during the execution of each algorithm, and the highest recorded memory consumption was noted. The results were then tabulated to compare the performance of each algorithm in terms of execution time and memory usage.

4. Results and Analysis

4.1. Comparison of Time Efficiency

This section conducts a comparison of the time efficiency among four KMP algorithm implementations: Basic KMP, KMP with nextval optimization, Boyer-Moore (BM), and Hybrid KMP-BM. Time efficiency measures the time taken by each algorithm to complete a search, which is crucial in determining their suitability for various scenarios.

The Basic KMP algorithm maintains a time complexity of O(n + m), consistent across test cases. The nextval optimization enhances efficiency by reducing redundant comparisons, particularly for patterns with repeating characters. Boyer-Moore outperforms KMP in cases with longer patterns due to its bad character heuristic, which skips large sections of the text. The Hybrid KMP-BM algorithm combines both methods, applying KMP to shorter patterns and BM to longer ones.

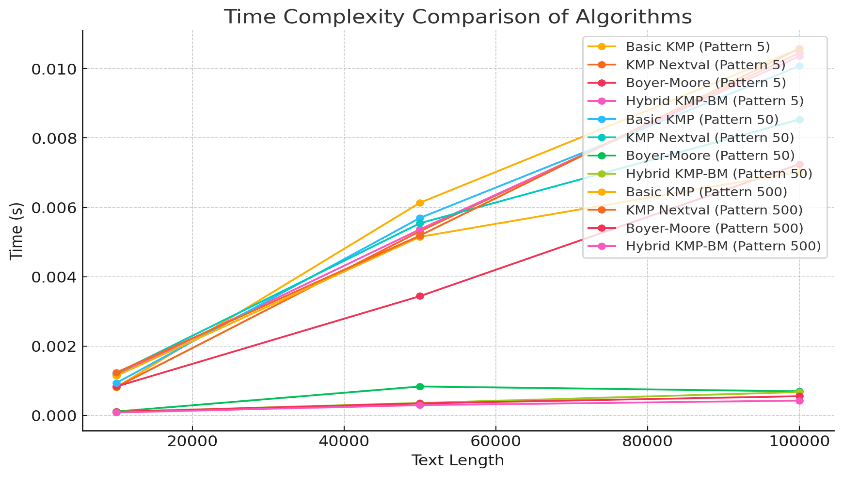
Figure 5: Time Complexity Comparison of Algorithms

From the experiments:

• For short patterns (length 5), Basic KMP and KMP Nextval performed similarly, with times around 0.0007s to 0.001s. Boyer-Moore was slightly slower, and Hybrid KMP-BM performed comparably to Basic KMP.

• For medium patterns (length 50), Boyer-Moore showed superior performance, with times as low as 0.000085s. Hybrid KMP-BM matched Boyer-Moore closely.

• For long patterns (length 500), Boyer-Moore and Hybrid KMP-BM continued to excel, with times between 0.000078s and 0.000345s, while Basic KMP and KMP Nextval lagged with times between 0.001398s and 0.010502s.

In conclusion, Boyer-Moore and Hybrid KMP-BM are best for longer patterns, while Basic KMP and KMP Nextval offer more consistent performance for smaller patterns.

4.2. Comparison of Space Efficiency

Space efficiency, or memory consumption, was measured using Python's memory profiler. The space complexity of Basic KMP is O(n + m), similar to KMP Nextval, which slightly alters memory usage for efficiency. Boyer-Moore requires extra memory for its bad character table, and Hybrid KMP-BM inherits the memory profiles of both KMP and BM.

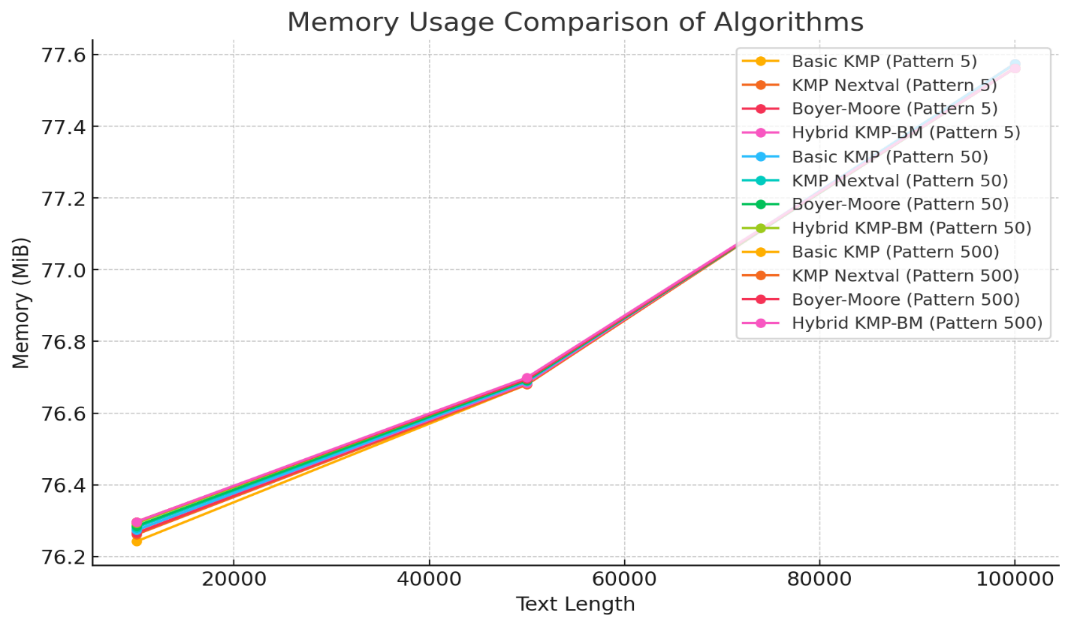
Figure 6: Memory Usage Comparison of Algorithms

Experimental results showed:

• For small text lengths (10,000 characters), all implementations used around 76.7 MiB of memory, with negligible differences.

• For medium text lengths (50,000 characters), memory usage rose slightly to 77.1 MiB, again with no significant variation.

• For large text lengths (100,000 characters), memory consumption remained around 77.1 MiB across all implementations.

In summary, no substantial memory differences were found among the implementations, suggesting that all are similarly space-efficient in Python. The choice of algorithm should be based primarily on time efficiency rather than memory consumption.

4.3. Comparison of Execution Efficiency

Execution efficiency, based on both time and space efficiency, was evaluated to determine the most effective algorithm for real-world applications.

The results indicated:

• Boyer-Moore and Hybrid KMP-BM were clearly superior in time efficiency for longer patterns, outperforming Basic KMP and KMP Nextval.

• For short patterns, all four algorithms performed similarly, making the choice of algorithm less critical for small patterns.

• Space efficiency was nearly identical across all implementations, so memory usage should not be a deciding factor.

Overall, Boyer-Moore and Hybrid KMP-BM are recommended for longer patterns due to their time efficiency, while Basic KMP and KMP Nextval are viable options for smaller patterns, offering consistent performance across all scenarios.

5. Conclusion

This study assessed the performance of four distinct implementations of the Knuth-Morris-Pratt (KMP) algorithm: Basic KMP, KMP with nextval optimization, Boyer-Moore, and Hybrid KMP-BM. The evaluation centered on time efficiency, space efficiency, and overall execution efficiency across different text and pattern lengths. Key findings include that time efficiency-wise, Boyer-Moore and Hybrid KMP-BM consistently outperformed the Basic KMP and KMP Nextval implementations for longer patterns. Boyer-Moore's bad character heuristic made it particularly effective for large-scale searches, while Basic KMP and KMP Nextval were more suited for shorter patterns. Regarding space efficiency, memory usage was consistent across all implementations, indicating that space complexity was not significantly affected by the specific algorithm used. In terms of execution efficiency, Boyer-Moore and Hybrid KMP-BM were the most efficient overall, especially for longer patterns. Basic KMP and KMP Nextval performed well for smaller patterns, but their execution times increased with longer patterns. In summary, Boyer-Moore and Hybrid KMP-BM are recommended for long-pattern searches, while Basic KMP and KMP Nextval are more appropriate for general use with shorter patterns. Future research focusing on parallelization, optimization, and real-world applications could enhance the algorithm's performance, scalability, and applicability across various fields.