1. Introduction
Decarbonization has been a major challenge for mankind[1, 2]. It demands a rethinking of the energy systems and requires the reduction of fossil-based energy sources and the adoption of clean energy. Hydrogen emerges as a promising fuel because of its high specific energy, renewability and its ability to be generated and consumed without the emission of greenhouse gasses[3]. However, the use of hydrogen is impeded by the lack of safe and cost-effective systems for H2 storage and transportation, with implementations on mobile (e.g. vehicular) platforms sometimes being more challenging than stationary applications[4]. To encourage research in this field, the US Department of Energy (DOE) has set the 2025-year (5.5 wt%, 40 g/L) and ultimate (6.5 wt%, 50 g/L) goals for storage systems[5]. To achieve this, significant attention has been paid to storage in solid adsorbent as an alternative to compression in high-pressure tanks[6, 7]. Solid adsorbents, such as metal hydrides, possess potential to exceed the storage capacities of physical storage methods at lower pressures and thus reduced cost [4, 8].
Metal-organic frameworks (MOFs) are a class of reticular coordinate materials composed of periodically arranged metal clusters and organic linkers[9]. Due to their reticular nature, MOFs are mostly crystalline and have unique properties compared with conventional solid materials (amorphous MOFs do exist but are not the focus of investigation in this work)[10, 11]. The porosity and high specific surface area make it ideal for the adsorption of small molecules, such as drugs, gasses, and metal complexes, leading to applications in drug delivery[12], gas storage and separation [13-15], and catalysis[16-18].Hydrogen storage as an applicational concern has been considered since the start of this class of materials marked by the development of MOF-5[19, 20]. Over the years, increasingly high-performance MOFs have been discovered, but the progress still falls behind the expectations outlined by the Department of Energy for adsorption rates. Thus, it is a pressing demand to develop materials with superior performance.
Computational screening approaches have significantly accelerated MOF materials design in the past years[21]. In silico materials design allows the researchers to exhaustively explore MOF materials that are not experimentally accessible[22]. A typical high throughput computational screening (HTCS) workflow starts with the generation of a MOF database covering diverse topology and compositions, followed by molecular modeling and calculation of target properties using classical or quantum mechanical methods[21-25]. Subsequently, top-performing MOFs are proposed for further experimental validation, with successful cases such as NU-800 for methane storage[26] and SBMOF-1 for Xe/Kr separation[27]. Such computational efforts in the past years, combined with experiments, have contributed to the construction of MOF databases (e.g., CoRE[28] MOF, hMOF[29]) with high quality crystal structures and properties, enabling the data-driven discovery of MOF materials[30,31]. Machine learning has received significant attention in materials science research, with great success in predicting materials properties, generating novel materials, and unraveling structure-property relationships[32-36]. There are several ways to represent a MOF structure including geometrical properties[37], string representations[38], energy grids[39], and graphs[40]. Among those, crystal graph convolutional neural network (CGCNN) is a widely used model for the prediction of the properties of inorganic crystals[40]. It represents a crystal structure as a graph comprising nodes for atoms and edges as bonds. CGCNN has been the basis of a multitude of graph neural network models for crystalline materials design, including the currently released MOFTransformer model[41]. By integrating ML into a HTCS workflow is anticipated to further facilitate the MOF design and discovery.
Herein, we propose a HTCS workflow, integrating molecular modeling and machine learning, and synthesizability ranking for designing MOF materials for H2 storage. We first analyzed the compositions of metals and metal clusters in experimental MOFs with superior H2 storage capacity. We then selected the most frequent metal clusters for the generation of a MOF database in combination with a range of organic linkers. The generated structures were then optimized to yield reasonable crystal structures. The volumetric and gravimetric H2 storage of the MOF prototypes were predicted by a MOFTransformer model trained on experimental MOFs with GCMC-determined H2 storage capacity. Through the study of a MOF database comprising of 2201 prototypes, we identified top performing MOFs with H2 storage capacities higher than MOF-5 and IRMOF-20. A free energy ranking of these MOFs showed the high synthetic likelihood for experimental testings. We found that the most abundant metal in these MOFs is Cu, indicating the importance of metal type choice in designing MOFs for H2 storage. In addition, we were able to examine the structure-property relationship indicating that the topology and geometry of MOFs are strongly associated with the H2 storage capacity, with a preference of low density and high surface area. It is anticipated that the HTCS workflow can be readily applied to MOF screening purposes for diverse applications, which can greatly accelerate MOF materials design compared with traditional experimental MOF screening protocol.
2. Methods
2.1. Structure Analysis of CoRE MOF
Prior to constructing the MOF database, we first investigated the structure composition of MOFs with high H2 storage capacities. On one hand, such analysis can help us understand the metal chemistry that dictates the ability of MOFs to absorb H2[42]. On the other hand, metals that usually possess poor H2 storage capacity can thus be discarded in subsequent MOF generation and screening to save computational resources. The dataset we used is reported by Ahmed and Siegel[43], which includes the CSD codes of the MOFs from multiple databases (CoRE MOF, hMOF etc.) and GCMC-calculated usable volumetric capacity and gravimetric capacity. The H2 storage capacity is calculated under pressure swing between 100 and 5 bar at 77K[43].
We focused on computation-ready experimental metal-organic framework (CoRE MOF) database as it is one of the most comprehensive MOF databases available open-source with over 14000 MOFs[28]. In total, we found around 6000 MOFs with matching crystal structures to the database mentioned before. To find the metals in the MOFs, we decomposed MOF structures using MOFID[44], which outputs the metal, linker, as well as the topology of a MOF with a given CIF file. Among the top-performing experimental MOFs, the abundance of metals was plotted and ranked as a histogram to identify the metals for subsequent study.
2.2. Hypothetical MOF Structure Generation
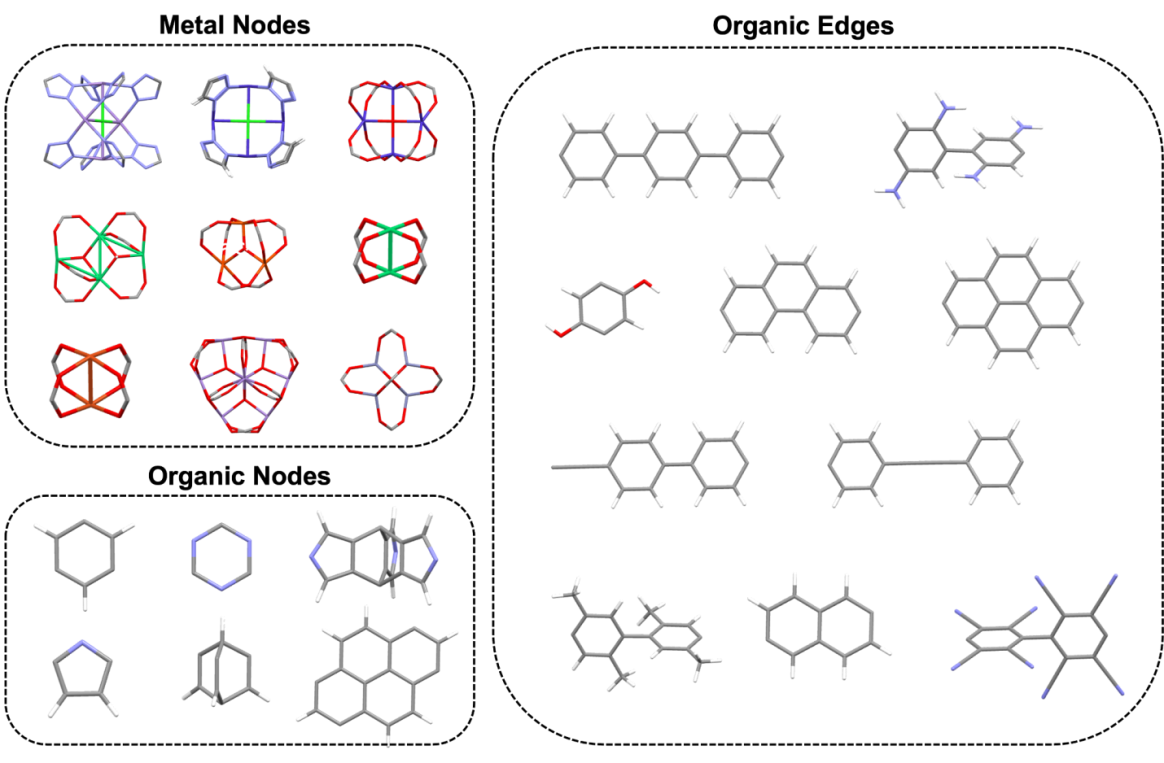
Figure 1: The building blocks for MOF database generation in ToBaCCo. The examples of the metal node, organic nodes and edges are visualized by Mercury.
In total, 10 metal clusters, 13 organic nodes and 36 organic linkers were selected to generate the MOF database for our study. Some example nodes and linkers are shown in Figure 1. The ToBaCCo code[29, 45] was used to create hypothetical MOF structures. Within the ToBaCCo code, there is a list of topology nets referenced from the Reticular Chemistry Structure Resource Database (RCSR)[46]. In practice, the code places the nodes and edges onto the reticular nets once a compatible topology is found, which is followed by a short structure minimization before outputting the CIF file. It should be noted that the MOF composition in this study is not exhaustive, and that one can easily generate more building units and structures. To ensure the synthetic feasibility of the generated MOF prototypes, we limit the edge combination in the ToBaCCo code as this implementation would usually lead to MOF unit cells with multiple different nodes and organic linkers[47]. We obtained a MOF database with 2201 structures using the selected building units and all the topologies included in the code.
2.3. Structure Optimization by MD Simulations
Since the ToBaCCo code generates MOFs purely relying on the geometry matching, the resulting structures may include severe atomic overlap or structure strains, which will lead to inaccuracy of the MOF geometric property calculations[48]. Thus, we used molecular dynamics (MD) simulation to relax the unit cells of the generated MOFs. MD simulation analyzes physical movements of atoms through simulating their interactions and dynamic evolution of the system. In our work, MD simulations were conducted using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) developed by Sandia National Laboratory[49]. The cif2lammps tool was used to generate the input files for LAMMPS with implementation of the UFF4MOF force field[50] containing corrected parameters for copper-paddle wheel metal nodes to represent the interatomic interaction. For structure energy minimization, a multi-stage scheme was performed. First, the box size and atom coordinates were minimized simultaneously. Secondly, the atomic coordinates were relaxed by fixing the box. The structure relaxation was stopped after three integrations. The final structures were then converted back to CIF format to give the final hypothetical MOF dataset. This dataset served as the basis of machine training and filtering for subsequent steps.
2.4. Calculation of MOF Geometrical Properties
To enable the relationship between H2 storage capacity and MOF structure, we obtained the MOF structural information using Zeo++[51], a software package specialized for the calculation of geometric parameters of crystalline porous materials. This is achieved through the application of Voronoi decomposition, which generates a graph representation of the void space in a given recursive structure. The most prominent among the parameters are density, pore sizes, surface area. A probe size of 1.86 Å is used in accordance with the diameter of N2, which is commonly used in experimental determination of MOF surface area. The specific properties we calculated include the largest cavity diameter (LCD), gravimetric surface area (GSA), density, and void fraction.
2.5. Hydrogen Storage Prediction by MOFTransformer
In principle, we can use grand canonical Monte Carlo (GCMC) simulations to calculate the H2 capacity of the generated MOFs. However, it is computationally demanding when the MOF space is large. Alternatively, machine learning offers an efficient and feasible way to determine the target properties of the newly generated MOFs. MOFTransformer is a deep-learning model specialized in predicting various properties of MOF materials[41]. It is pretrained on over 1 million MOF structures to learn the underlying structural properties of MOFs. Through subsequent fine-tuning with specifically curated datasets oriented towards MOFs with properties in hydrogen uptake, the model is readied to evaluate the hydrogen storage capacities of the generated hypothetical MOFs[52]. The graph representation and energy grid embeddings are used to represent a MOF structure. The crystal graph is derived from CGCNN[38] and the energy grids[53] are calculated with methane as a simulated probe molecule using the Universal Force Field (UFF)[54] and Transferable Potentials for Phase Equilibria (TraPPE)[55] Force Field.
The data set used for training includes 5920 MOFs with gravimetric capacity and volumetric capacity labels as reported in ref[43]. The corresponding crystal structures are taken from the CoRE MOF dataset. A ratio of 0.7:0.15:0.15 was used to split data into training, validation, and test data sets. The batch size was set to 36 to accumulate the training gradient and the maximum epochs was 500. The training was conducted on 1 GPU node (NVIDIA GeForce RTX 4090) with CUDA version of 12.2. We visualized the training progress using the tensor board built in PyTorch to ensure the convergence of the loss and to avoid overfitting during the model training.
2.6. Synthesizability Evaluation of Proposed MOF Structures
2.6.1. Structure Equilibration
All simulations and calculations were performed using molecular dynamics in LAMMPS, with a time step of 1 fs. The parameterization of MOFs was obtained using the same protocol for the structure optimization. The resulting topologies were first energy minimized using the conjugate gradient algorithm to eliminate any forces on atoms larger than 1 x 10-15 kcal/mol.Å, followed by a short NPT equilibration under 0 bar and 300 K maintained by Nose-Hoover barostat and thermostat, respectively, over a course of 200 ps. Then the box was further relaxed using the fix box/relax code which allowed the adjustment of the simulation box. The volume was then saved for final analysis, and the final structures were saved for subsequent free energy calculations.
2.6.2. Free Energy Calculation by the Frenkel Ladd Path
To compute the free energy of a solid, we employed the Frenkel Ladd path described in detail in the work by Freitas[56]. Briefly, the FL free energy is computed by thermodynamic integration (TI) from an Einstein crystal to a fully interacting solids. With the addition of the analytical free energy of the reference Einstein crystal, we can obtain the absolute free energy of MOF crystals for synthesizability comparison. The employment of free energy has been reported to well predict whether the MOF can be synthesized in experiments. Einstein crystal describes a system in which each atom is coupled to its defined equilibrium position by a harmonic potential using a force field representation. During the TI process, an initial system is switched to a final system using a scaled potential energy
\( H(λ)=λ{H_{1}}+(1-λ){H_{0}} \) (1)
where is a coupling parameter within [0,1]. The system corresponds to an Einstein crystal (U0) when = 0 and to a fully interacting MOF solids (U1) at = 1. The free energy between the two states can be calculated using
\( ΔF=\int _{0}^{1}〈\frac{∂U}{∂λ}〉dλ \) (2)
where \( 〈\frac{∂U}{∂λ}〉 \) is the ensemble average at a specific \( λ \) point. Since the free energy of an Einstein crystal is known and we can compute the absolute free energy F of a MOF solid,
\( F= ΔF+3{k_{B}}T\sum _{i}^{N}ln{(\frac{ħω}{{k_{B}}T})} \) (3)
where is the vibration frequency associated with each atom, ħ is the reduced Plank’s constant, and N is the number of atoms. The vibrational frequency is controlled by the force constant associated to each atom. In an Einstein crystal, the force constant can be arbitrary but more reliable results can be acquired when the reference state resembles the real solid. Thus, we used a uniform constant of 10 kcal/mol/Å2 for all atoms, which has been reported to perform well for MOF solids.
To enhance the computational efficiency, a non-equilibrium switching method was used, where becomes a time-dependent value. The free energy associated between Einstein crystal and the final solid can be estimated by the average work done by a forward switching and backward switching,
\( ΔF=\frac{1}{2}(W_{0→1}^{irr}-W_{1→0}^{irr}) \) (4)
where W is the irreversible work during the non-equilibrium switching. Finally, we add a correction term to compensate the translation entropy loss when we removed the center of mass translation of the solid,
\( {F_{correction}}={k_{B}}Tln(\frac{{n_{r}}}{V} {(2π{k_{B}}T\sum _{i}^{N}\frac{μ_{i}^{2}}{{α_{i}}} )^{\frac{3}{2}}}) \) (5)
where \( {μ_{i}}= {m_{i}}/\sum _{i}{m_{i}} \) , and \( {n_{r}} \) is the number of unit cell replications used in the simulation, and 𝑉 is the equilibrium volume.
3. Results and Discussion
3.1. Structure Analysis of CoREMOF
Due to the modular nature, MOF materials, in principle, can be assembled from diverse metal nodes and organic linkers, leading to an infinite number of MOF prototypes[57]. To make our computational screening tractable, we first analyzed the structure compositions of top-performing MOFs from a subset of experimental crystals and then selected the top metal nodes for subsequent structure generation. The distributions of usable volumetric capacity (VC) and gravimetric capacity (GC) are shown in Figure 2a, 2b. The majority of the MOFs are distributed over a region with moderate usable VC while over a region with low usable GC. In our study, a VC threshold of 35 g/L and a GC threshold of 3.5 wt% are used to determine the best MOFs, which comprises 27.3% of the MOFs. The metal composition of as-selected structures is shown in Figure 2c. It is obvious that Zn and Cu are the most prevalent metals existing in the optimal MOFs for H2 storage, indicating that Zn or Cu may offer metal sites that interact with H2. Thus, we hypothesize that utilizing the most frequent metal types for constructing the hypothetical MOF structures may increase the possibility of identifying MOFs with higher performances and reduce the computational efforts on poor performance of MOFs composed of less frequent metals. To this regard, the top six metals, including Zn, Cu, Co, Ni, Mn, and Fe, are selected leading to a total of 10 metal clusters with distinct topologies.
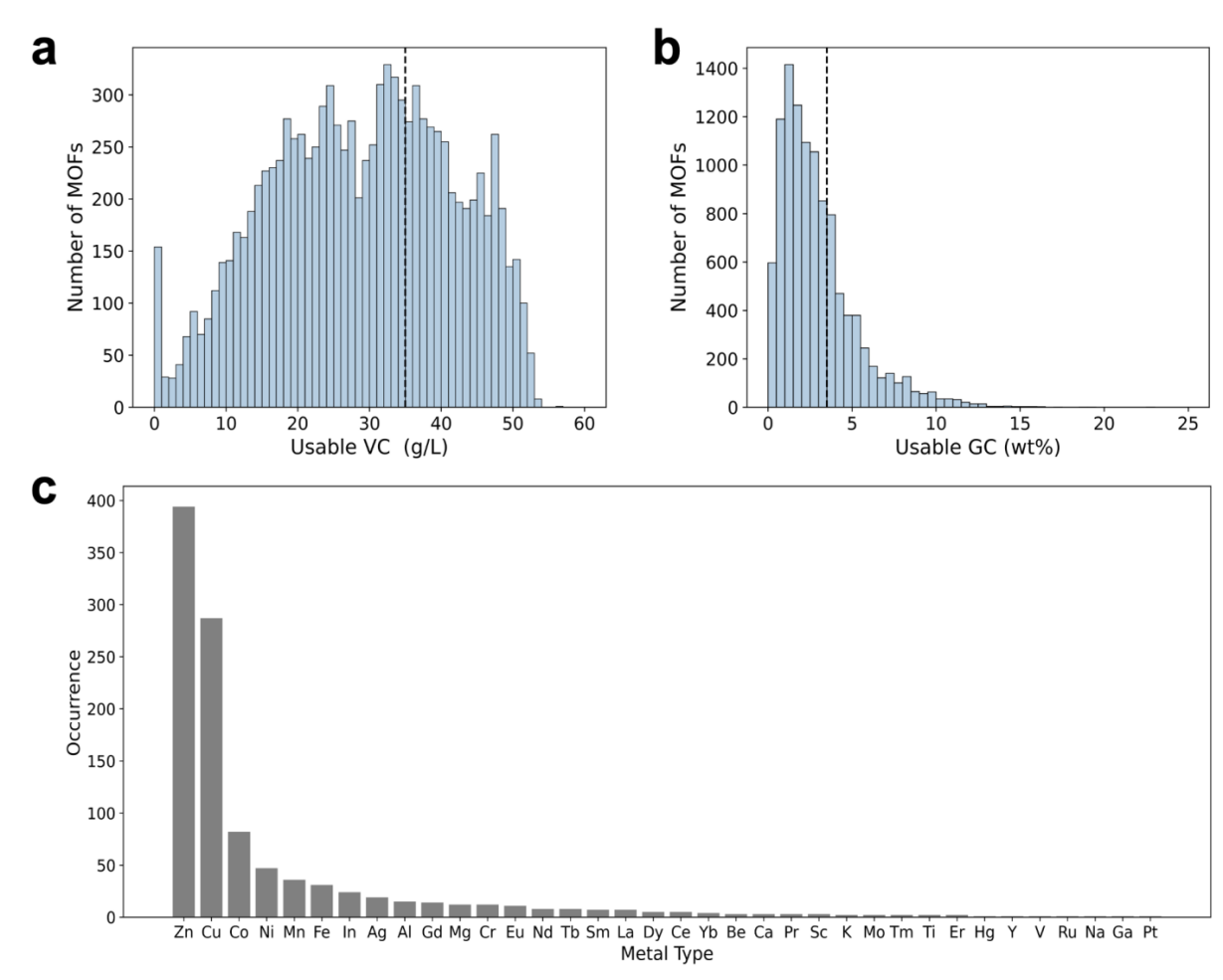
Figure 2: Analysis of MOFs from the experimental MOFs. The histogram plots of (a) usable volumetric H2 capacity and (b) usable gravimetric H2 capacity. The dashed lines are the arbitrary thresholds used to select the top-performing MOFs. (c) The occurrence of metals in the selected MOFs.
3.2. Generation and Structural Optimization of MOFs
During the MOF generation, we enforced the resulting MOFs to contain only one metal type under the consideration of synthesis feasibility. In addition, we leave out the linkers with sulfur atoms because they do not or rarely appear in the CoRE MOF database. The MOF structures created by ToBaCCo may be distorted from a usual crystal structure with long bonds or atomic overlap, which hinders the performance of subsequent machine learning algorithms when converting the MOFs to graph and energy grid representations. Therefore, we use MD simulations to optimize all the MOF prototypes. As shown in Figure 3a, the as-generated structures have long distances between the connecting site of the metal cluster and that of the linker. After geometry optimization by force field calculations, this structural distortion can be eliminated (Figure 3b). Ideally, density functional theory calculation would be used for such purposes, while it is quite computational expensive especially in the context of high throughput screening. The MD simulation with the use of the UFF4MOF force field is adequate as proven by literature[58].
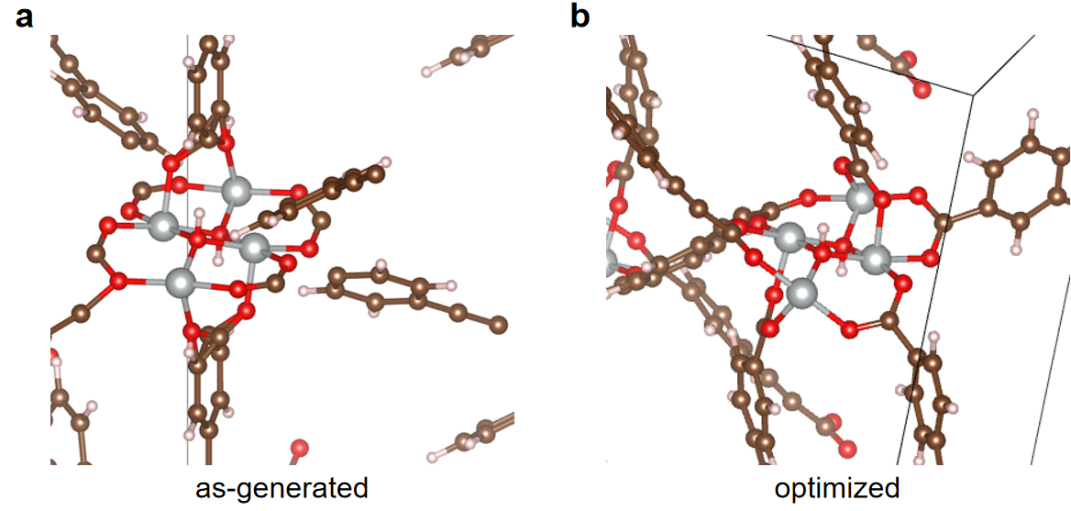
Figure 3: One example shows the MOF structure generated by ToBaCCo without geometry optimization (a) as compared with the structure after geometry optimization (b).
3.3. H2 Storage Capacity Prediction by MOFTransformer
The MOFTransformer model is one of the state of art models for porous materials capable of tasks of regression, classification and so forth. The model is trained separately for VC capacity and GC capacity. Figure 4 shows the scatter plots of the comparison between predicted and calculated H2 storage capacity. The gray dots, which represent the training data, are well aligned on the diagonal line indicating that training data has been well fitted. To examine how the model extrapolates to the unseen data, the results of the test data set for VC and GC are shown as blue in Figure 4a and 4b. It is obvious that the regression performance for the test data is not as good as the training set with more scattered dots along the diagonal line. This is expected because the trained model has never visited the MOF structures in the test set. For VC, the R2 of the test set is 0.862 and the mean absolute error (MAE) is 2.663 g/L; and for GC, the R2 of the test set is 0.870 and the MAE is 0.394 wt%. These results suggest that the MOFTransformer model is properly trained to predict the corresponding properties in our self-constructed MOF database.
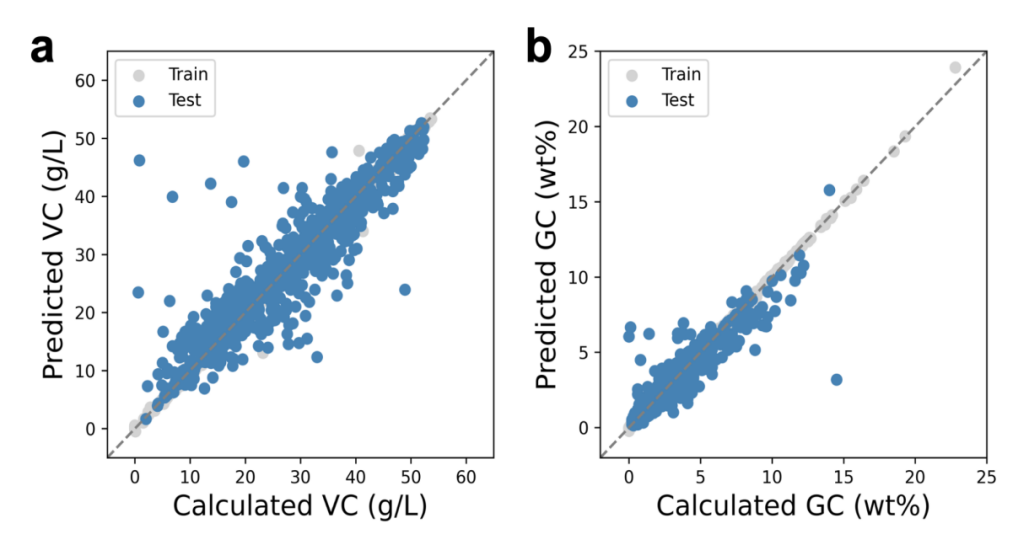
Figure 4: The scatter plot shows the comparison between predicted and calculated (a) VC and (b) GC for MOFs in the data set. The gray dots are MOFs in the training set and the blue dots are the MOFs in the testing set.
3.4. Relationship Between H2 Storage Capacity and MOF Geometric Properties
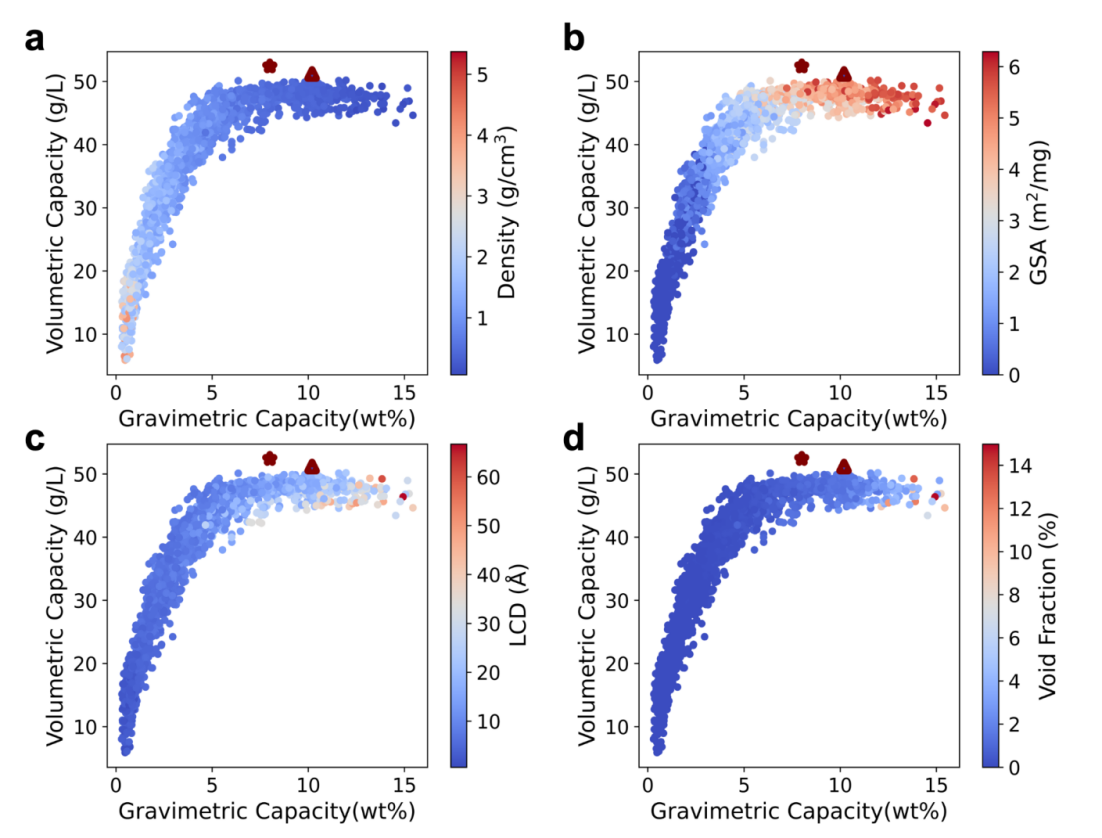
Figure 5: Relationship between H2 capacity and MOF geometric properties. The predicted VC is plotted against GC, with the color bars showing the (a) density, (b) GSA, (c) LCD, and (d) void fraction of the MOFs. The star and the triangle dots show the MOF-5 and IRMOF-20, respectively, as the reference.
With the optimized MOF database comprising 2201 MOF prototypes and the fine-tuned MOFTransformer models, we then proceeded to predict the VC and GC. One advantage of high-throughput screening in a large MOF space is that it allows us to investigate the relationship between H2 storage capacity and MOF structures. For such purpose, we extracted the MOF geometric properties for all optimized MOFs. As shown in Figure 5, VC increases as GC increases and then plateaus when GC reaches around 5 wt%. The majority of the high-performing MOFs have a density lower than 2 g/cm3 (Figure 5a). It is reasonable because a large void volume would offer more space for adsorbed H2 molecules, leading to low density MOF structures. This also aligns with the relationship for LCD and void fraction shown in Figure 5c and 5d, due to the strong correlation between density and void fraction and LCD in MOFs. Notably, we find that the GC is highly related to the GSA of MOFs (Figure 5b), with the majority of the top-performing MOFs possessing GSA values larger than 3.0 m2/mg.
Generally, in our MOF database, the majority of MOFs still reside in the poor or moderate H2 storage area. We find that MOFs with larger pores, lower densities, larger void fractions would usually have higher GC and VC values. However, when the MOF reaches a certain condition (e.g., density < 2g/cm3), the VC reaches a plateau while the GC continues to increase to ~ 15 wt%. Based on this, it can be envisioned that MOFs with densities beyond the lower bound of our dataset, may start to show degrading VC performances due to the increasing unoccupied volumes in these low-density MOFs. Therefore, to design MOFs with both high VC and GC performances, the region where VC plateaus and GC continues increasing should be targeted as in our study. However, we cannot make the conclusion that the VC values studied here is the limit due to the finite MOF space we explored.
3.5. Proposed Structures
The star- and triangle- shaped dots represent MOF-5 and IRMOF-20 as reference structures (Figure 5). Despite the fact that the VC of our generated MOFs fall below those of MOF-5 and IRMOF-20, we do identify a region of MOFs with GC exceeding the reference structures. To define a metric to screen the top MOFs, we use a simple product of GC and VC to rank the MOFs, which is inspired by the fact that researchers prefer MOFs with both high GC and VC. Finally, we were able to select the top 5 performing MOFs as summarized in Table 1 and visualized in Figure 6. As shown in Table 1, we can see that the GC and VC of the proposed structures fall in the upper right tip region in Figure 5, indicating the ability of the product of GC and VC to identify best-performing MOFs. Another parameter to select top MOFs is to sum the ranks for GC and VC for each MOF. This is similarly guided by the idea that both indices should be considered when evaluating the adsorption of MOFs. The top 5 MOFs selected this way are shown in Table 2:
Table 1: Proposed MOF structures selected from the whole database with their additional properties.
Ranking | Topology | Metal SBU Type | GC (wt%) | VC (g/L) | Density (g/cm3) |
1 | umx | 3c-Cu | 15.16 | 48.95 | 0.21 |
2 | ete | 3c-Cu | 15.24 | 46.88 | 0.10 |
3 | sod | 4c-Cu | 15.05 | 46.78 | 0.22 |
4 | etc | 3c-Cu | 14.92 | 46.36 | 0.061 |
5 | cdsa | 3c-Cu | 15.44 | 44.63 | 0.091 |
Table 2: Top-performing proposed MOF structures selected from the whole database with their additional properties according to ranking of GC and VC.
Ranking | Topology | Metal SBU Type | GC (wt%) | VC (g/L) | GC Ranking | VC Ranking | Density (g/cm3) |
1 | bod | 3c-Cu | 13.84 | 49.21 | 13 | 31 | 0.070 |
2 | wjh | 4c-Cu | 13.20 | 49.31 | 22 | 25 | 0.18 |
3 | umx | 4c-Cu | 15.16 | 48.95 | 3 | 45 | 0.21 |
4 | umf | 4c-Cu | 11.96 | 50.18 | 66 | 2 | 0.20 |
5 | unc | 4c-Ni | 11.80 | 49.51 | 78 | 17 | 0.27 |
Surprisingly, we find that the metal type consistently to be Cu instead of Zn in the top 5 structures. Copper-based SBUs are the second most abundant in top performing MOFs in the CoRE MOF database, which implies that MOFs with copper as metal clusters may be underexplored experimentally for H2 storage purposes and that attempts to synthesize copper-based MOFs may lead to better MOF materials. Nickel, the fourth most abundant metal in the CoRE MOF database, might also be underrepresented in prior investigation on H2 storage MOFs. In many cases, Ni-based MOFs perform comparably with Cu-based MOFs with the same topology. Additionally, consistent with the results in Section 3.4, the proposed MOFs have low densities, exhibiting large pores and channels in the structures (Figure 6).
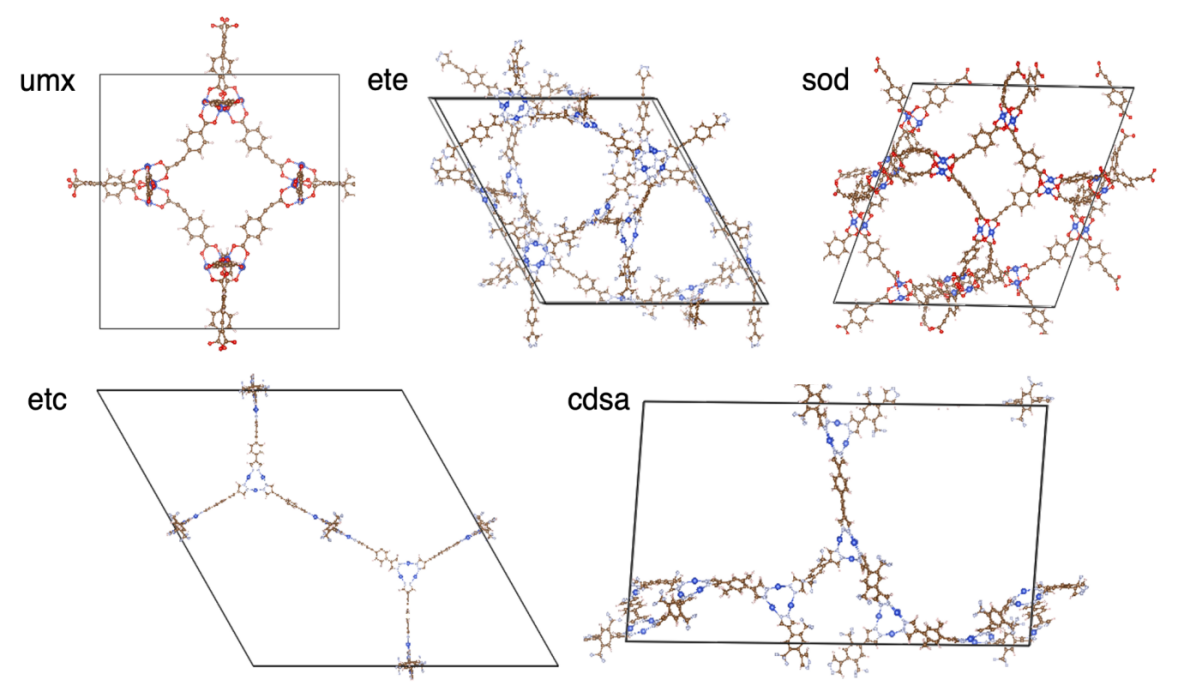
Figure 6: Five top-performing MOFs for optimal H2 storage identified from our database as listed in Table 1. The metal type for all five structures is Cu.
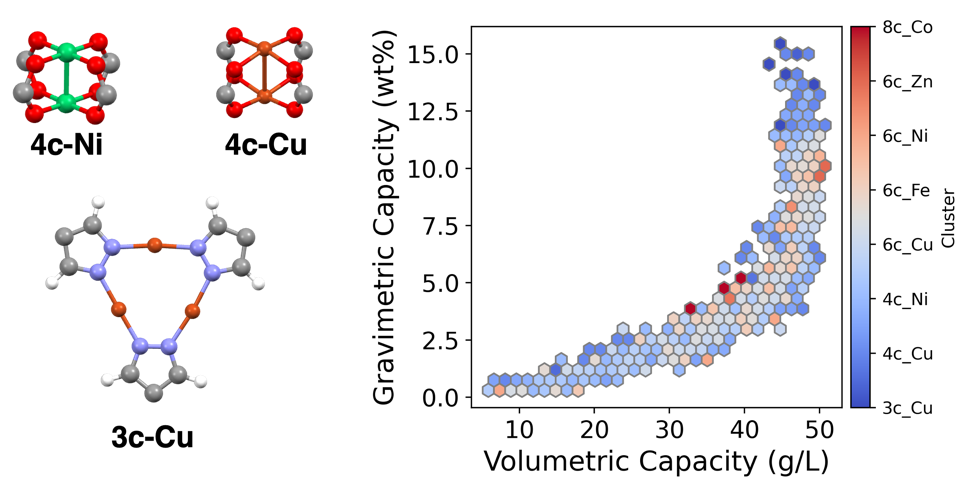
Figure 7: The frequent clusters in top-performing MOFs as revealed from the high throughput screening. The 3c_Cu cluster, shown as the bluest color, persistently cluster in the upper corner region with high hydrogen storage capacity.
From the above results, the top-performing MOFs are also overwhelmingly based on 4c-Cu, 4c-Ni, and 3c-Cu. There is compelling evidence that in addition to the superiority of Cu-based SBUs in H2 storage, 3c-Cu SBUs consistently exhibit better performance compared to 4c-Cu SBUs as shown in Figure 7. The MOFs with 3c-Cu SBUs are consistently in the high-performance region. This might be accredited to the fact that 3c-Cu is a SBU that contains 3 Cu atoms with coordination number of each being 2. In comparison, 4c-Cu is a SBU that has two Cu atom with coordination number of each being 4. The lower coordination number for 3c-Cu suggest that it can provide more open metal sites for MOF to interact with H2 and thus increase the adsorption[42]. Despite only accounting for 1% of all hypothetical MOFs tested, it appears disproportionately frequently on the top of the list, with 5 occurrences in the top 20. Thus, future experiments attempts may devote more attention to low coordinated Cu metal clusters for constructing MOFs with optimal hydrogen storage.
3.6. Can the Proposed MOFs be Synthesized?
The next question we seek to answer is whether these MOFs are likely to be synthesized experimentally. Despite the potency of HTVS to discover high performing MOFs, the generated hypothetical MOFs from previous workflows are noted for their vacant frameworks and low densities, and thus are not guaranteed to be synthesized in labs. This suggests probable deviation of experimental results with computational prediction, which has been seen in a number of HTVS work where the predicted MOFs are not the one synthesized in experiments. Thus, it is critical to evaluate the synthesizability of the proposed MOFs to refine the HTVS workflow[24, 25, 58].
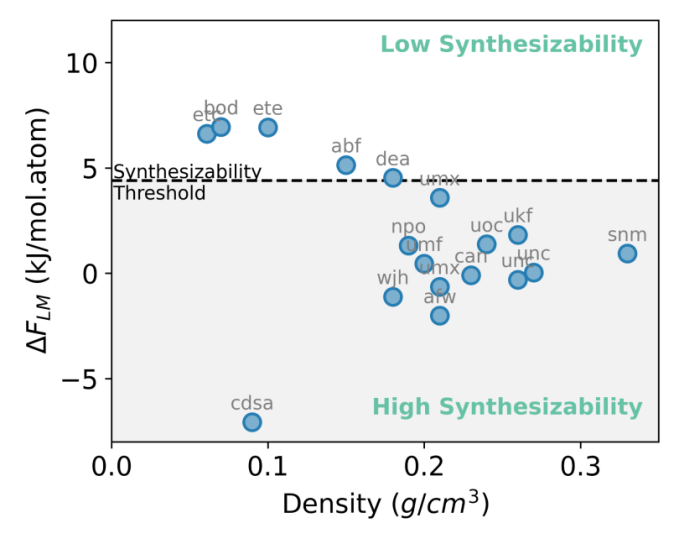
Figure 8: Free energy profiles of the top 18 MOF structures from the ranking from Table 1 and 2. The free energy is linearly transformed according to the work by Anderson[59] treating all MOFs as the Cu MOF set for simplicity. The dashed line indicates the threshold for synthetically probable MOFs.
The Frenkel Ladd Path free energies of the top 10 MOFs in each ranking were computed to rank the synthesizability of MOFs (in total 18 structures as bod appears in both and sod too skewed) (Figure 8). Notably, the Frenkel Ladd Path did not apply successfully onto every top-performing MOF. For example, the MOF enumerated in Table 1 that sod topology was too unstable and skewed to be calculated by our simulation pathway, and thus its absolute free energy result is absent. By defining a free energy threshold of 4.4 kJ/mol.atom, under which MOFs are likely to be synthesized, we note that the majority of the proposed MOFs possess high synthetic likelihood, with the wjh, umx, unc, umf, and npo (Table 1, 2) being the top 5 stable MOFs. Although above the threshold, the etc, bod, ete structures still have low free energies. In addition, we also observe that the free energy, i.e., synthesizability, has a strong correlation with density[59],which is in accordance with experimental findings that a closely packed crystals are favored to porous materials.
The further evaluation of the synthesizability of proposed MOFs strengthens our computational prediction of the top-performing and high-synthesizability MOFs. The free energy ranking also guides the experimentalists to prioritize the attempts on MOFs that are of higher synthesizability when comparable H2 storage capacities are identified.
4. Conclusions and Discussions
In summary, we propose a high throughput screening workflow for discovering MOFs with optimal H2 storage capacities. The workflow starts with the construction of a user-defined hypothetical MOF database followed by MD simulations for structure optimization. Then, we fine-tune a pre-trained MOFTransformer model as a surrogate model to predict the target properties of interest (i.e., H2 storage capacity) and to identify top-performing MOFs. The MOF geometric properties are also computed to allow for the investigation of structure-property relationships. In addition, the workflow utilized machine learning models for property estimation, which is highly efficient in the purpose of high throughput screening. We also performed prediction of MOF stability (i.e., synthesizability) for the top ones using free energy calculation, showing that the proposed structures generally have high synthesizability. Although having limited data, we observe that dense structures are characterized by higher stability. Essentially, the workflow holds great promise for MOF screening because it can be readily applied to other applications, such as gas separation and conductivity, as long as there are experimental or computed properties for a large MOF database. We foresee that with the advancement of cheminformatics and databases, leveraging molecule modeling and machine learning techniques can open up new avenues for materials design.
Through the study of 2201 MOF prototypes that we generated in this work, we find that MOFs with low density and high surface areas are preferred for H2 storage. This agrees with experimental findings and intuitions because lower density can offer space for H2 storage while high surface area can maximize the interaction between MOFs and H2 molecules. In addition, we identified 5 best-performing MOFs with GC higher than MOF-5 and IRMOF-20. Unfortunately, the VC does not outperform those but are of similar values. Notably, the top MOFs all use copper as the metal clusters, in particular the 3c-Cu cluster. This emphasizes the importance of low coordination Cu cluster in future computational and experimental screening of MOFs for hydrogen storage. In addition, the Frenkel Ladd path free energy calculation revealed that the majority of the MOFs we proposed are of high synthesizability and thus are promising for experimental tryout.
Despite its findings, however, we note that this work is still limited both in terms of breadth of the scope of the MOFs considered in the generation process and the evaluation of the properties of these generated MOFs. Firstly, this work only considered a limited selection of SBUs, and only considered MOFs constructed with one type of metallic center and linker each. Considering the reported high performance of mixed-metal MOFs[60, 61] and the multitude of topologies made available, further research may take these additional possibilities into account. Moreover, current MOFs often possess sub-ambient or even cryogenic too low to be practically applicable in real-life settings, especially onboard individual vehicles[62]. Further research could devise novel algorithms to simulate and predict the working temperature of generated MOFs as well. Another characteristic worth investigating is the structural durability, or resistance to structural collapse. MOFs are crystalline, but with repeated filling and depleting of solution molecules, it may generate an amorphous phase, undermining the framework’s ability to store hydrogen[63].
References
[1]. Papadis, E.; Tsatsaronis, G. Challenges in the decarbonization of the energy sector. Energy 2020, 205, 118025. DOI: https://doi.org/10.1016/j.energy.2020.118025.
[2]. Daehn, K.; Basuhi, R.; Gregory, J.; Berlinger, M.; Somjit, V.; Olivetti, E. A. Innovations to decarbonize materials industries. Nature Reviews Materials 2022, 7 (4), 275-294. DOI: 10.1038/s41578-021-00376-y.
[3]. Odenweller, A.; Ueckerdt, F.; Nemet, G. F.; Jensterle, M.; Luderer, G. Probabilistic feasibility space of scaling up green hydrogen supply. Nature Energy 2022, 7 (9), 854-865. DOI: 10.1038/s41560-022-01097-4.
[4]. Eberle, U.; Felderhoff, M.; Schüth, F. Chemical and Physical Solutions for Hydrogen Storage. Angew Chem Int Edit 2009, 48 (36), 6608-6630. DOI: 10.1002/anie.200806293.
[5]. DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles. 2023. DOI: https://www.energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles.
[6]. Huang, Y.; Cheng, Y.; Zhang, J. A Review of High Density Solid Hydrogen Storage Materials by Pyrolysis for Promising Mobile Applications. Industrial & Engineering Chemistry Research 2021, 60 (7), 2737-2771. DOI: 10.1021/acs.iecr.0c04387.
[7]. Wang, Y.; Xue, Y.; Zuttel, A. Nanoscale engineering of solid-state materials for boosting hydrogen storage. Chem Soc Rev 2024, 53 (2), 972-1003. DOI: 10.1039/d3cs00706e From NLM PubMed-not-MEDLINE.
[8]. Chen, S.; Jelic, J.; Rein, D.; Najafishirtari, S.; Schmidt, F. P.; Girgsdies, F.; Kang, L.; Wandzilak, A.; Rabe, A.; Doronkin, D. E.; et al. Highly loaded bimetallic iron-cobalt catalysts for hydrogen release from ammonia. Nat Commun 2024, 15 (1), 871. DOI: 10.1038/s41467-023-44661-6 From NLM PubMed-not-MEDLINE.
[9]. Furukawa, H.; Cordova, K. E.; O’Keeffe, M.; Yaghi, O. M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341 (6149), 1230444. DOI: doi:10.1126/science.1230444.
[10]. Fonseca, J.; Gong, T. H.; Jiao, L.; Jiang, H. L. Metal-organic frameworks (MOFs) beyond crystallinity: amorphous MOFs, MOF liquids and MOF glasses. J Mater Chem A 2021, 9 (17), 10562-10611. DOI: 10.1039/d1ta01043c.
[11]. Yaghi, O. M. Reticular Chemistry-Construction, Properties, and Precision Reactions of Frameworks. Journal of the American Chemical Society 2016, 138 (48), 15507-15509. DOI: 10.1021/jacs.6b11821.
[12]. Luo, T.; Ni, K.; Culbert, A.; Lan, G.; Li, Z.; Jiang, X.; Kaufmann, M.; Lin, W. Nanoscale Metal–Organic Frameworks Stabilize Bacteriochlorins for Type I and Type II Photodynamic Therapy. J Am Chem Soc 2020, 142 (16), 7334-7339. DOI: 10.1021/jacs.0c02129.
[13]. Alezi, D.; Belmabkhout, Y.; Suyetin, M.; Eddaoudi, M. MOF crystal chemistry paving the way to gas storage needs: Aluminum-based soc-MOF for CH4, O2, and CO2 storage. Abstr Pap Am Chem S 2016, 251.
[14]. Jiang, S. Y.; Sun, H.; Gong, K.; Huang, X.; Zhu, Y. H.; Feng, X.; Xie, J.; Liu, J. Y.; Wang, B. Metal-Organic Frameworks for Breakthrough Separation of 2-Butene Isomers with High Dynamic Selectivity and Capacity. Angew Chem Int Edit 2023. DOI: 10.1002/anie.202302036.
[15]. Yaghi, O. M. Systematic design of pore size and functionality in isoreticular MOFs. Abstr Pap Am Chem S 2004, 228, U780-U780.
[16]. Sadakiyo, M. Support effects of metal-organic frameworks in heterogeneous catalysis. Nanoscale 2022, 14 (9), 3398-3406. DOI: 10.1039/d1nr07659k.
[17]. Wang, Q.; Astruc, D. State of the Art and Prospects in Metal-Organic Framework (MOF)-Based and MOF-Derived Nanocatalysis. Chemical Reviews 2020, 120 (2), 1438-1511. DOI: 10.1021/acs.chemrev.9b00223.
[18]. García-García, P.; Müller, M.; Corma, A. MOF catalysis in relation to their homogeneous counterparts and conventional solid catalysts. Chemical Science 2014, 5 (8), 2979-3007. DOI: 10.1039/c4sc00265b.
[19]. Rosi, N. L.; Eckert, J.; Eddaoudi, M.; Vodak, D. T.; Kim, J.; O'Keeffe, M.; Yaghi, O. M. Hydrogen storage in microporous metal-organic frameworks. Science 2003, 300 (5622), 1127-1129. DOI: DOI 10.1126/science.1083440.
[20]. Bordiga, S.; Vitillo, J. G.; Ricchiardi, G.; Regli, L.; Cocina, D.; Zecchina, A.; Arstad, B.; Bjorgen, M.; Hafizovic, J.; Lillerud, K. P. Interaction of hydrogen with MOF-5. J Phys Chem B 2005, 109 (39), 18237-18242. DOI: 10.1021/jp052611p.
[21]. Daglar, H.; Keskin, S. Computational Screening of Metal-Organic Frameworks for Membrane-Based CO2/N2/H2O Separations: Best Materials for Flue Gas Separation. J Phys Chem C 2018, 122 (30), 17347-17357. DOI: 10.1021/acs.jpcc.8b05416.
[22]. Moghadam, P. Z.; Chung, Y. G.; Snurr, R. Q. Progress toward the computational discovery of new metal-organic framework adsorbents for energy applications. Nature Energy 2024. DOI: 10.1038/s41560-023-01417-2.
[23]. Lin, Y. C.; Cheng, R. H.; Liang, T. G.; Wu, W. X.; Li, S.; Li, W. Understanding the influence of secondary building units on the thermal conductivity of metal-organic frameworks via high-throughput computational screening. Phys Chem Chem Phys 2023. DOI: 10.1039/d3cp04640k.
[24]. Altintas, C.; Erucar, I.; Keskin, S. High-Throughput Computational Screening of the Metal Organic Framework Database for CH4/H2 Separations. Acs Appl Mater Inter 2018, 10 (4), 3668-3679. DOI: 10.1021/acsami.7b18037.
[25]. Ponraj, Y. K.; Borah, B. High-Throughput Computational Screening of Metal-Organic Frameworks for the Separation of Methane from Ethane and Propane. J Phys Chem C 2021, 125 (3), 1839-1854. DOI: 10.1021/acs.jpcc.0c09117.
[26]. Gomez-Gualdron, D. A.; Gutov, O. V.; Krungleviciute, V.; Borah, B.; Mondloch, J. E.; Hupp, J. T.; Yildirim, T.; Farha, O. K.; Snurr, R. Q. Computational Design of Metal-Organic Frameworks Based on Stable Zirconium Building Units for Storage and Delivery of Methane. Chem Mater 2014, 26 (19), 5632-5639. DOI: 10.1021/cm502304e.
[27]. Banerjee, D.; Simon, C. M.; Plonka, A. M.; Motkuri, R. K.; Liu, J.; Chen, X. Y.; Smit, B.; Parise, J. B.; Haranczyk, M.; Thallapally, P. K. Metal-organic framework with optimally selective xenon adsorption and separation. Nature Communications 2016, 7. DOI: ARTN 1183110.1038/ncomms11831.
[28]. Chung, Y. G.; Haldoupis, E.; Bucior, B. J.; Haranczyk, M.; Lee, S.; Zhang, H.; Vogiatzis, K. D.; Milisavljevic, M.; Ling, S.; Camp, J. S.; et al. Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019. Journal of Chemical & Engineering Data 2019, 64 (12), 5985-5998. DOI: 10.1021/acs.jced.9b00835.
[29]. Majumdar, S.; Moosavi, S. M.; Jablonka, K. M.; Ongari, D.; Smit, B. Diversifying Databases of Metal Organic Frameworks for High-Throughput Computational Screening. Acs Appl Mater Inter 2021, 13 (51), 61004-61014. DOI: 10.1021/acsami.1c16220.
[30]. Boyd, P. G.; Chidambaram, A.; García-Díez, E.; Ireland, C. P.; Daff, T. D.; Bounds, R.; Gladysiak, A.; Schouwink, P.; Moosavi, S. M.; Maroto-Valer, M. M.; et al. Data-driven design of metal-organic frameworks for wet flue gas CO capture. Nature 2019, 576 (7786), 253-+. DOI: 10.1038/s41586-019-1798-7.
[31]. Rosen, A. S.; Notestein, J. M.; Snurr, R. Q. Realizing the data-driven, computational discovery of metal-organic framework catalysts. Curr Opin Chem Eng 2022, 35. DOI: ARTN 3510.1016/j.coche.2021.100760.
[32]. Suh, C.; Fare, C.; Warren, J. A.; Pyzer-Knapp, E. O. Evolving the Materials Genome: How Machine Learning Is Fueling the Next Generation of Materials Discovery. Annu Rev Mater Res 2020, 50, 1-25. DOI: 10.1146/annurev-matsci-082019-105100.
[33]. Oda, H.; Kiyohara, S.; Mizoguchi, T. Machine learning for structure determination and investigating the structure-property relationships of interfaces. J Phys-Mater 2019, 2 (3). DOI: ARTN 03400510.1088/2515-7639/ab15c8.
[34]. Sun, B. C.; Barnard, A. S. Visualising multi-dimensional structure/property relationships with machine learning. J Phys-Mater 2019, 2 (3). DOI: ARTN 03400310.1088/2515-7639/ab0faa.
[35]. Altintas, C.; Altundal, O. F.; Keskin, S.; Yildirim, R. Machine Learning Meets with Metal Organic Frameworks for Gas Storage and Separation. Journal of Chemical Information and Modeling 2021, 61 (5), 2131-2146. DOI: 10.1021/acs.jcim.1c00191.
[36]. Yao, Z.; Sánchez-Lengeling, B.; Bobbitt, N. S.; Bucior, B. J.; Kumar, S. G. H.; Collins, S. P.; Burns, T.; Woo, T. K.; Farha, O. K.; Snurr, R. Q.; et al. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nature Machine Intelligence 2021, 3 (1), 76-86. DOI: 10.1038/s42256-020-00271-1.
[37]. Chong, S.; Lee, S.; Kim, B.; Kim, J. Applications of machine learning in metal-organic frameworks. Coordination Chemistry Reviews 2020, 423. DOI: ARTN 21348710.1016/j.ccr.2020.213487.
[38]. Cao, Z. L.; Magar, R.; Wang, Y. Y.; Farimani, A. B. MOFormer: Self-Supervised Transformer Model for Metal-Organic Framework Property Prediction. Journal of the American Chemical Society 2023. DOI: 10.1021/jacs.2c11420.
[39]. Bucior, B. J.; Bobbitt, N. S.; Islamoglu, T.; Goswami, S.; Gopalan, A.; Yildirim, T.; Farha, O. K.; Bagheri, N.; Snurr, R. Q. Energy-based descriptors to rapidly predict hydrogen storage in metal-organic frameworks. Mol Syst Des Eng 2019, 4 (1), 162-174. DOI: 10.1039/c8me00050f.
[40]. Xie, T.; Grossman, J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys Rev Lett 2018, 120 (14). DOI: ARTN 14530110.1103/PhysRevLett.120.145301.
[41]. Kang, Y. H.; Park, H.; Smit, B.; Kim, J. A multi-modal pre-training transformer for universal transfer learning in metal-organic frameworks. Nature Machine Intelligence 2023, 5 (3), 309-318. DOI: 10.1038/s42256-023-00628-2.
[42]. Sengupta, D.; Melix, P.; Bose, S.; Duncan, J.; Wang, X.; Mian, M. R.; Kirlikovali, K. O.; Joodaki, F.; Islamoglu, T.; Yildirim, T.; et al. Air-Stable Cu(I) Metal-Organic Framework for Hydrogen Storage. J Am Chem Soc 2023, 145 (37), 20492-20502. DOI: 10.1021/jacs.3c06393 From NLM PubMed-not-MEDLINE.
[43]. Ahmed, A.; Siegel, D. J. Predicting hydrogen storage in MOFs via machine learning. Patterns (N Y) 2021, 2 (7), 100291. DOI: 10.1016/j.patter.2021.100291 From NLM PubMed-not-MEDLINE.
[44]. Bucior, B. J.; Rosen, A. S.; Haranczyk, M.; Yao, Z. P.; Ziebel, M. E.; Farha, O. K.; Hupp, J. T.; Siepmann, J. I.; Aspuru-Guzik, A.; Snurr, R. Q. Identification Schemes for Metal-Organic Frameworks To Enable Rapid Search and Cheminformatics Analysis. Cryst Growth Des 2019, 19 (11), 6682-6697. DOI: 10.1021/acs.cgd.9b01050.
[45]. Colón, Y. J.; Gómez-Gualdrón, D. A.; Snurr, R. Q. Topologically Guided, Automated Construction of Metal-Organic Frameworks and Their Evaluation for Energy-Related Applications. Cryst Growth Des 2017, 17 (11), 5801-5810. DOI: 10.1021/acs.cgd.7b00848.
[46]. O'Keeffe, M.; Peskov, M. A.; Ramsden, S. J.; Yaghi, O. M. The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, Crystal Nets. Accounts Chem Res 2008, 41 (12), 1782-1789. DOI: 10.1021/ar800124u.
[47]. Yuan, S.; Qin, J. S.; Li, J.; Huang, L.; Feng, L.; Fang, Y.; Lollar, C.; Pang, J.; Zhang, L.; Sun, D.; et al. Retrosynthesis of multi-component metal-organic frameworks. Nat Commun 2018, 9 (1), 808. DOI: 10.1038/s41467-018-03102-5 From NLM PubMed-not-MEDLINE.
[48]. Fung, V.; Zhang, J. X.; Juarez, E.; Sumpter, B. G. Benchmarking graph neural networks for materials chemistry. Npj Computational Materials 2021, 7 (1). DOI: ARTN 8410.1038/s41524-021-00554-0.
[49]. Thompson, A. P.; Aktulga, H. M.; Berger, R.; Bolintineanu, D. S.; Brown, W. M.; Crozier, P. S.; Veld, P. J. I.; Kohlmeyer, A.; Moore, S. G.; Nguyen, T. D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput Phys Commun 2022, 271. DOI: ARTN 10817110.1016/j.cpc.2021.108171.
[50]. Coupry, D. E.; Addicoat, M. A.; Heine, T. Extension of the Universal Force Field for Metal-Organic Frameworks. Journal of Chemical Theory and Computation 2016, 12 (10), 5215-5225. DOI: 10.1021/acs.jctc.6b00664.
[51]. Willems, T. F.; Rycroft, C.; Kazi, M.; Meza, J. C.; Haranczyk, M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Micropor Mesopor Mat 2012, 149 (1), 134-141. DOI: 10.1016/j.micromeso.2011.08.020.
[52]. Hosna, A.; Merry, E.; Gyalmo, J.; Alom, Z.; Aung, Z.; Azim, M. A. Transfer learning: a friendly introduction. J Big Data-Ger 2022, 9 (1). DOI: ARTN 102 10.1186/s40537-022-00652-w.
[53]. Li, Z.; Bucior, B. J.; Chen, H. Y.; Haranczyk, M.; Siepmann, J. I.; Snurr, R. Q. Machine learning using host/guest energy histograms to predict adsorption in metal-organic frameworks: Application to short alkanes and Xe/Kr mixtures. Journal of Chemical Physics 2021, 155 (1). DOI: Artn 01470110.1063/5.0050823.
[54]. Rappe, A. K.; Casewit, C. J.; Colwell, K. S.; Goddard, W. A.; Skiff, W. M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. Journal of the American Chemical Society 1992, 114 (25), 10024-10035. DOI: 10.1021/ja00051a040.
[55]. Bai, P.; Tsapatsis, M.; Siepmann, J. I. TraPPE-zeo: Transferable Potentials for Phase Equilibria Force Field for All-Silica Zeolites. J Phys Chem C 2013, 117 (46), 24375-24387. DOI: 10.1021/jp4074224.
[56]. Freitas, R.; Asta, M.; de Koning, M. Nonequilibrium free-energy calculation of solids using LAMMPS. Computational Materials Science 2016, 112, 333-341. DOI: https://doi.org/10.1016/j.commatsci.2015.10.050.
[57]. Zhou, H.-C. J.; Kitagawa, S. Metal–Organic Frameworks (MOFs). Chemical Society Reviews 2014, 43 (16), 5415-5418, 10.1039/C4CS90059F. DOI: 10.1039/C4CS90059F.
[58]. Islamov, M.; Babaei, H.; Anderson, R.; Sezginel, K. B.; Long, J. R.; McGaughey, A. J. H.; Gomez-Gualdron, D. A.; Wilmer, C. E. High-throughput screening of hypothetical metal-organic frameworks for thermal conductivity. Npj Computational Materials 2023, 9 (1). DOI: ARTN 11 10.1038/s41524-022-00961-x.
[59]. Anderson, R.; Gómez-Gualdrón, D. A. Large-Scale Free Energy Calculations on a Computational Metal–Organic Frameworks Database: Toward Synthetic Likelihood Predictions. Chem Mater 2020, 32 (19), 8106-8119. DOI: 10.1021/acs.chemmater.0c00744.
[60]. Abednatanzi, S.; Gohari Derakhshandeh, P.; Depauw, H.; Coudert, F.-X.; Vrielinck, H.; Van Der Voort, P.; Leus, K. Mixed-metal metal–organic frameworks. Chemical Society Reviews 2019, 48 (9), 2535-2565, 10.1039/C8CS00337H. DOI: 10.1039/C8CS00337H.
[61]. Masoomi, M. Y.; Morsali, A.; Dhakshinamoorthy, A.; Garcia, H. Mixed-Metal MOFs: Unique Opportunities in Metal-Organic Framework (MOF) Functionality and Design. Angew Chem Int Ed Engl 2019, 58 (43), 15188-15205. DOI: 10.1002/anie.201902229 From NLM PubMed-not-MEDLINE.
[62]. Dodson, R. A.; Wong-Foy, A. G.; Matzger, A. J. The Metal–Organic Framework Collapse Continuum: Insights from Two-Dimensional Powder X-ray Diffraction. Chem Mater 2018, 30 (18), 6559-6565. DOI: 10.1021/acs.chemmater.8b03378.
Cite this article
Liu,Z. (2025). High Throughput Virtual Screening of Metal-Organic Frameworks for Hydrogen Storage. Applied and Computational Engineering,123,119-133.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 5th International Conference on Materials Chemistry and Environmental Engineering
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Papadis, E.; Tsatsaronis, G. Challenges in the decarbonization of the energy sector. Energy 2020, 205, 118025. DOI: https://doi.org/10.1016/j.energy.2020.118025.
[2]. Daehn, K.; Basuhi, R.; Gregory, J.; Berlinger, M.; Somjit, V.; Olivetti, E. A. Innovations to decarbonize materials industries. Nature Reviews Materials 2022, 7 (4), 275-294. DOI: 10.1038/s41578-021-00376-y.
[3]. Odenweller, A.; Ueckerdt, F.; Nemet, G. F.; Jensterle, M.; Luderer, G. Probabilistic feasibility space of scaling up green hydrogen supply. Nature Energy 2022, 7 (9), 854-865. DOI: 10.1038/s41560-022-01097-4.
[4]. Eberle, U.; Felderhoff, M.; Schüth, F. Chemical and Physical Solutions for Hydrogen Storage. Angew Chem Int Edit 2009, 48 (36), 6608-6630. DOI: 10.1002/anie.200806293.
[5]. DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles. 2023. DOI: https://www.energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles.
[6]. Huang, Y.; Cheng, Y.; Zhang, J. A Review of High Density Solid Hydrogen Storage Materials by Pyrolysis for Promising Mobile Applications. Industrial & Engineering Chemistry Research 2021, 60 (7), 2737-2771. DOI: 10.1021/acs.iecr.0c04387.
[7]. Wang, Y.; Xue, Y.; Zuttel, A. Nanoscale engineering of solid-state materials for boosting hydrogen storage. Chem Soc Rev 2024, 53 (2), 972-1003. DOI: 10.1039/d3cs00706e From NLM PubMed-not-MEDLINE.
[8]. Chen, S.; Jelic, J.; Rein, D.; Najafishirtari, S.; Schmidt, F. P.; Girgsdies, F.; Kang, L.; Wandzilak, A.; Rabe, A.; Doronkin, D. E.; et al. Highly loaded bimetallic iron-cobalt catalysts for hydrogen release from ammonia. Nat Commun 2024, 15 (1), 871. DOI: 10.1038/s41467-023-44661-6 From NLM PubMed-not-MEDLINE.
[9]. Furukawa, H.; Cordova, K. E.; O’Keeffe, M.; Yaghi, O. M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341 (6149), 1230444. DOI: doi:10.1126/science.1230444.
[10]. Fonseca, J.; Gong, T. H.; Jiao, L.; Jiang, H. L. Metal-organic frameworks (MOFs) beyond crystallinity: amorphous MOFs, MOF liquids and MOF glasses. J Mater Chem A 2021, 9 (17), 10562-10611. DOI: 10.1039/d1ta01043c.
[11]. Yaghi, O. M. Reticular Chemistry-Construction, Properties, and Precision Reactions of Frameworks. Journal of the American Chemical Society 2016, 138 (48), 15507-15509. DOI: 10.1021/jacs.6b11821.
[12]. Luo, T.; Ni, K.; Culbert, A.; Lan, G.; Li, Z.; Jiang, X.; Kaufmann, M.; Lin, W. Nanoscale Metal–Organic Frameworks Stabilize Bacteriochlorins for Type I and Type II Photodynamic Therapy. J Am Chem Soc 2020, 142 (16), 7334-7339. DOI: 10.1021/jacs.0c02129.
[13]. Alezi, D.; Belmabkhout, Y.; Suyetin, M.; Eddaoudi, M. MOF crystal chemistry paving the way to gas storage needs: Aluminum-based soc-MOF for CH4, O2, and CO2 storage. Abstr Pap Am Chem S 2016, 251.
[14]. Jiang, S. Y.; Sun, H.; Gong, K.; Huang, X.; Zhu, Y. H.; Feng, X.; Xie, J.; Liu, J. Y.; Wang, B. Metal-Organic Frameworks for Breakthrough Separation of 2-Butene Isomers with High Dynamic Selectivity and Capacity. Angew Chem Int Edit 2023. DOI: 10.1002/anie.202302036.
[15]. Yaghi, O. M. Systematic design of pore size and functionality in isoreticular MOFs. Abstr Pap Am Chem S 2004, 228, U780-U780.
[16]. Sadakiyo, M. Support effects of metal-organic frameworks in heterogeneous catalysis. Nanoscale 2022, 14 (9), 3398-3406. DOI: 10.1039/d1nr07659k.
[17]. Wang, Q.; Astruc, D. State of the Art and Prospects in Metal-Organic Framework (MOF)-Based and MOF-Derived Nanocatalysis. Chemical Reviews 2020, 120 (2), 1438-1511. DOI: 10.1021/acs.chemrev.9b00223.
[18]. García-García, P.; Müller, M.; Corma, A. MOF catalysis in relation to their homogeneous counterparts and conventional solid catalysts. Chemical Science 2014, 5 (8), 2979-3007. DOI: 10.1039/c4sc00265b.
[19]. Rosi, N. L.; Eckert, J.; Eddaoudi, M.; Vodak, D. T.; Kim, J.; O'Keeffe, M.; Yaghi, O. M. Hydrogen storage in microporous metal-organic frameworks. Science 2003, 300 (5622), 1127-1129. DOI: DOI 10.1126/science.1083440.
[20]. Bordiga, S.; Vitillo, J. G.; Ricchiardi, G.; Regli, L.; Cocina, D.; Zecchina, A.; Arstad, B.; Bjorgen, M.; Hafizovic, J.; Lillerud, K. P. Interaction of hydrogen with MOF-5. J Phys Chem B 2005, 109 (39), 18237-18242. DOI: 10.1021/jp052611p.
[21]. Daglar, H.; Keskin, S. Computational Screening of Metal-Organic Frameworks for Membrane-Based CO2/N2/H2O Separations: Best Materials for Flue Gas Separation. J Phys Chem C 2018, 122 (30), 17347-17357. DOI: 10.1021/acs.jpcc.8b05416.
[22]. Moghadam, P. Z.; Chung, Y. G.; Snurr, R. Q. Progress toward the computational discovery of new metal-organic framework adsorbents for energy applications. Nature Energy 2024. DOI: 10.1038/s41560-023-01417-2.
[23]. Lin, Y. C.; Cheng, R. H.; Liang, T. G.; Wu, W. X.; Li, S.; Li, W. Understanding the influence of secondary building units on the thermal conductivity of metal-organic frameworks via high-throughput computational screening. Phys Chem Chem Phys 2023. DOI: 10.1039/d3cp04640k.
[24]. Altintas, C.; Erucar, I.; Keskin, S. High-Throughput Computational Screening of the Metal Organic Framework Database for CH4/H2 Separations. Acs Appl Mater Inter 2018, 10 (4), 3668-3679. DOI: 10.1021/acsami.7b18037.
[25]. Ponraj, Y. K.; Borah, B. High-Throughput Computational Screening of Metal-Organic Frameworks for the Separation of Methane from Ethane and Propane. J Phys Chem C 2021, 125 (3), 1839-1854. DOI: 10.1021/acs.jpcc.0c09117.
[26]. Gomez-Gualdron, D. A.; Gutov, O. V.; Krungleviciute, V.; Borah, B.; Mondloch, J. E.; Hupp, J. T.; Yildirim, T.; Farha, O. K.; Snurr, R. Q. Computational Design of Metal-Organic Frameworks Based on Stable Zirconium Building Units for Storage and Delivery of Methane. Chem Mater 2014, 26 (19), 5632-5639. DOI: 10.1021/cm502304e.
[27]. Banerjee, D.; Simon, C. M.; Plonka, A. M.; Motkuri, R. K.; Liu, J.; Chen, X. Y.; Smit, B.; Parise, J. B.; Haranczyk, M.; Thallapally, P. K. Metal-organic framework with optimally selective xenon adsorption and separation. Nature Communications 2016, 7. DOI: ARTN 1183110.1038/ncomms11831.
[28]. Chung, Y. G.; Haldoupis, E.; Bucior, B. J.; Haranczyk, M.; Lee, S.; Zhang, H.; Vogiatzis, K. D.; Milisavljevic, M.; Ling, S.; Camp, J. S.; et al. Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019. Journal of Chemical & Engineering Data 2019, 64 (12), 5985-5998. DOI: 10.1021/acs.jced.9b00835.
[29]. Majumdar, S.; Moosavi, S. M.; Jablonka, K. M.; Ongari, D.; Smit, B. Diversifying Databases of Metal Organic Frameworks for High-Throughput Computational Screening. Acs Appl Mater Inter 2021, 13 (51), 61004-61014. DOI: 10.1021/acsami.1c16220.
[30]. Boyd, P. G.; Chidambaram, A.; García-Díez, E.; Ireland, C. P.; Daff, T. D.; Bounds, R.; Gladysiak, A.; Schouwink, P.; Moosavi, S. M.; Maroto-Valer, M. M.; et al. Data-driven design of metal-organic frameworks for wet flue gas CO capture. Nature 2019, 576 (7786), 253-+. DOI: 10.1038/s41586-019-1798-7.
[31]. Rosen, A. S.; Notestein, J. M.; Snurr, R. Q. Realizing the data-driven, computational discovery of metal-organic framework catalysts. Curr Opin Chem Eng 2022, 35. DOI: ARTN 3510.1016/j.coche.2021.100760.
[32]. Suh, C.; Fare, C.; Warren, J. A.; Pyzer-Knapp, E. O. Evolving the Materials Genome: How Machine Learning Is Fueling the Next Generation of Materials Discovery. Annu Rev Mater Res 2020, 50, 1-25. DOI: 10.1146/annurev-matsci-082019-105100.
[33]. Oda, H.; Kiyohara, S.; Mizoguchi, T. Machine learning for structure determination and investigating the structure-property relationships of interfaces. J Phys-Mater 2019, 2 (3). DOI: ARTN 03400510.1088/2515-7639/ab15c8.
[34]. Sun, B. C.; Barnard, A. S. Visualising multi-dimensional structure/property relationships with machine learning. J Phys-Mater 2019, 2 (3). DOI: ARTN 03400310.1088/2515-7639/ab0faa.
[35]. Altintas, C.; Altundal, O. F.; Keskin, S.; Yildirim, R. Machine Learning Meets with Metal Organic Frameworks for Gas Storage and Separation. Journal of Chemical Information and Modeling 2021, 61 (5), 2131-2146. DOI: 10.1021/acs.jcim.1c00191.
[36]. Yao, Z.; Sánchez-Lengeling, B.; Bobbitt, N. S.; Bucior, B. J.; Kumar, S. G. H.; Collins, S. P.; Burns, T.; Woo, T. K.; Farha, O. K.; Snurr, R. Q.; et al. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nature Machine Intelligence 2021, 3 (1), 76-86. DOI: 10.1038/s42256-020-00271-1.
[37]. Chong, S.; Lee, S.; Kim, B.; Kim, J. Applications of machine learning in metal-organic frameworks. Coordination Chemistry Reviews 2020, 423. DOI: ARTN 21348710.1016/j.ccr.2020.213487.
[38]. Cao, Z. L.; Magar, R.; Wang, Y. Y.; Farimani, A. B. MOFormer: Self-Supervised Transformer Model for Metal-Organic Framework Property Prediction. Journal of the American Chemical Society 2023. DOI: 10.1021/jacs.2c11420.
[39]. Bucior, B. J.; Bobbitt, N. S.; Islamoglu, T.; Goswami, S.; Gopalan, A.; Yildirim, T.; Farha, O. K.; Bagheri, N.; Snurr, R. Q. Energy-based descriptors to rapidly predict hydrogen storage in metal-organic frameworks. Mol Syst Des Eng 2019, 4 (1), 162-174. DOI: 10.1039/c8me00050f.
[40]. Xie, T.; Grossman, J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys Rev Lett 2018, 120 (14). DOI: ARTN 14530110.1103/PhysRevLett.120.145301.
[41]. Kang, Y. H.; Park, H.; Smit, B.; Kim, J. A multi-modal pre-training transformer for universal transfer learning in metal-organic frameworks. Nature Machine Intelligence 2023, 5 (3), 309-318. DOI: 10.1038/s42256-023-00628-2.
[42]. Sengupta, D.; Melix, P.; Bose, S.; Duncan, J.; Wang, X.; Mian, M. R.; Kirlikovali, K. O.; Joodaki, F.; Islamoglu, T.; Yildirim, T.; et al. Air-Stable Cu(I) Metal-Organic Framework for Hydrogen Storage. J Am Chem Soc 2023, 145 (37), 20492-20502. DOI: 10.1021/jacs.3c06393 From NLM PubMed-not-MEDLINE.
[43]. Ahmed, A.; Siegel, D. J. Predicting hydrogen storage in MOFs via machine learning. Patterns (N Y) 2021, 2 (7), 100291. DOI: 10.1016/j.patter.2021.100291 From NLM PubMed-not-MEDLINE.
[44]. Bucior, B. J.; Rosen, A. S.; Haranczyk, M.; Yao, Z. P.; Ziebel, M. E.; Farha, O. K.; Hupp, J. T.; Siepmann, J. I.; Aspuru-Guzik, A.; Snurr, R. Q. Identification Schemes for Metal-Organic Frameworks To Enable Rapid Search and Cheminformatics Analysis. Cryst Growth Des 2019, 19 (11), 6682-6697. DOI: 10.1021/acs.cgd.9b01050.
[45]. Colón, Y. J.; Gómez-Gualdrón, D. A.; Snurr, R. Q. Topologically Guided, Automated Construction of Metal-Organic Frameworks and Their Evaluation for Energy-Related Applications. Cryst Growth Des 2017, 17 (11), 5801-5810. DOI: 10.1021/acs.cgd.7b00848.
[46]. O'Keeffe, M.; Peskov, M. A.; Ramsden, S. J.; Yaghi, O. M. The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, Crystal Nets. Accounts Chem Res 2008, 41 (12), 1782-1789. DOI: 10.1021/ar800124u.
[47]. Yuan, S.; Qin, J. S.; Li, J.; Huang, L.; Feng, L.; Fang, Y.; Lollar, C.; Pang, J.; Zhang, L.; Sun, D.; et al. Retrosynthesis of multi-component metal-organic frameworks. Nat Commun 2018, 9 (1), 808. DOI: 10.1038/s41467-018-03102-5 From NLM PubMed-not-MEDLINE.
[48]. Fung, V.; Zhang, J. X.; Juarez, E.; Sumpter, B. G. Benchmarking graph neural networks for materials chemistry. Npj Computational Materials 2021, 7 (1). DOI: ARTN 8410.1038/s41524-021-00554-0.
[49]. Thompson, A. P.; Aktulga, H. M.; Berger, R.; Bolintineanu, D. S.; Brown, W. M.; Crozier, P. S.; Veld, P. J. I.; Kohlmeyer, A.; Moore, S. G.; Nguyen, T. D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput Phys Commun 2022, 271. DOI: ARTN 10817110.1016/j.cpc.2021.108171.
[50]. Coupry, D. E.; Addicoat, M. A.; Heine, T. Extension of the Universal Force Field for Metal-Organic Frameworks. Journal of Chemical Theory and Computation 2016, 12 (10), 5215-5225. DOI: 10.1021/acs.jctc.6b00664.
[51]. Willems, T. F.; Rycroft, C.; Kazi, M.; Meza, J. C.; Haranczyk, M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Micropor Mesopor Mat 2012, 149 (1), 134-141. DOI: 10.1016/j.micromeso.2011.08.020.
[52]. Hosna, A.; Merry, E.; Gyalmo, J.; Alom, Z.; Aung, Z.; Azim, M. A. Transfer learning: a friendly introduction. J Big Data-Ger 2022, 9 (1). DOI: ARTN 102 10.1186/s40537-022-00652-w.
[53]. Li, Z.; Bucior, B. J.; Chen, H. Y.; Haranczyk, M.; Siepmann, J. I.; Snurr, R. Q. Machine learning using host/guest energy histograms to predict adsorption in metal-organic frameworks: Application to short alkanes and Xe/Kr mixtures. Journal of Chemical Physics 2021, 155 (1). DOI: Artn 01470110.1063/5.0050823.
[54]. Rappe, A. K.; Casewit, C. J.; Colwell, K. S.; Goddard, W. A.; Skiff, W. M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. Journal of the American Chemical Society 1992, 114 (25), 10024-10035. DOI: 10.1021/ja00051a040.
[55]. Bai, P.; Tsapatsis, M.; Siepmann, J. I. TraPPE-zeo: Transferable Potentials for Phase Equilibria Force Field for All-Silica Zeolites. J Phys Chem C 2013, 117 (46), 24375-24387. DOI: 10.1021/jp4074224.
[56]. Freitas, R.; Asta, M.; de Koning, M. Nonequilibrium free-energy calculation of solids using LAMMPS. Computational Materials Science 2016, 112, 333-341. DOI: https://doi.org/10.1016/j.commatsci.2015.10.050.
[57]. Zhou, H.-C. J.; Kitagawa, S. Metal–Organic Frameworks (MOFs). Chemical Society Reviews 2014, 43 (16), 5415-5418, 10.1039/C4CS90059F. DOI: 10.1039/C4CS90059F.
[58]. Islamov, M.; Babaei, H.; Anderson, R.; Sezginel, K. B.; Long, J. R.; McGaughey, A. J. H.; Gomez-Gualdron, D. A.; Wilmer, C. E. High-throughput screening of hypothetical metal-organic frameworks for thermal conductivity. Npj Computational Materials 2023, 9 (1). DOI: ARTN 11 10.1038/s41524-022-00961-x.
[59]. Anderson, R.; Gómez-Gualdrón, D. A. Large-Scale Free Energy Calculations on a Computational Metal–Organic Frameworks Database: Toward Synthetic Likelihood Predictions. Chem Mater 2020, 32 (19), 8106-8119. DOI: 10.1021/acs.chemmater.0c00744.
[60]. Abednatanzi, S.; Gohari Derakhshandeh, P.; Depauw, H.; Coudert, F.-X.; Vrielinck, H.; Van Der Voort, P.; Leus, K. Mixed-metal metal–organic frameworks. Chemical Society Reviews 2019, 48 (9), 2535-2565, 10.1039/C8CS00337H. DOI: 10.1039/C8CS00337H.
[61]. Masoomi, M. Y.; Morsali, A.; Dhakshinamoorthy, A.; Garcia, H. Mixed-Metal MOFs: Unique Opportunities in Metal-Organic Framework (MOF) Functionality and Design. Angew Chem Int Ed Engl 2019, 58 (43), 15188-15205. DOI: 10.1002/anie.201902229 From NLM PubMed-not-MEDLINE.
[62]. Dodson, R. A.; Wong-Foy, A. G.; Matzger, A. J. The Metal–Organic Framework Collapse Continuum: Insights from Two-Dimensional Powder X-ray Diffraction. Chem Mater 2018, 30 (18), 6559-6565. DOI: 10.1021/acs.chemmater.8b03378.









