1. Introduction

Deep learning is a subset of machine learning that focuses on using artificial neural networks to model and understand complex patterns in data.

Neural networks are computational models inspired by the human brain. They consist of layers of nodes, each layer transforming the input data through mathematical functions. The first layer receives the raw input data, while hidden layers extract higher-level features. The final layer produces the output, such as classifications or predictions.

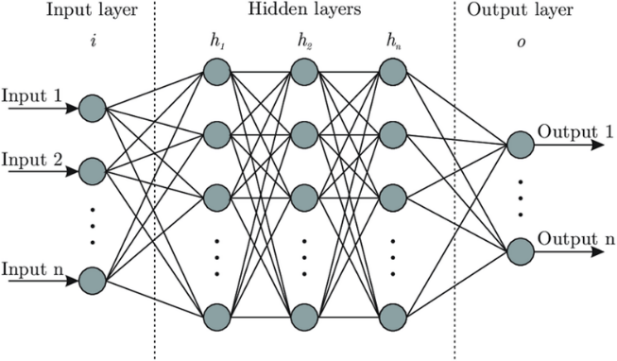
Figure 1: A typical neural network structure.

Neural networks have numerous applications in science and engineering due to their ability to model complex relationships and make predictions based on data. Image Recognition, Natural Language Processing, and Predictive Modeling are some of the popular use cases of neural networks.

However, this traditional neural network structure only focuses on the data it is given and neglects the vast amount of prior knowledge, like laws of physics or some empirically validated rules. This means that traditional neural networks are extremely dependent on the quantity and quality of the training data they are given. However, often, while analyzing complex physical, biological, or engineering systems, the cost of data acquisition is prohibitive, and we are inevitably faced with the challenge of drawing conclusions and making decisions under partial information. In this small data regime, most state-of-the-art machine learning techniques (e.g., deep/convolutional/recurrent neural networks) lack robustness and fail to provide any guarantees of convergence.[1]

The concept of Physics-Informed Neural Networks (PINNs) was proposed to solve the mentioned problem by M. Raissi, P. Perdikaris, and G.E. Karniadakis [1]. Physics-Informed Neural Networks utilize artificial neural networks to solve problems governed by partial differential equations (PDEs) or other physics laws.

PINNs extend traditional neural networks by computing things like partial derivatives of the output variables in terms of the input variables. Then, we use the results to create additional loss functions called physics losses that are governed by PDEs or other physics laws so that the neural network is physics informed. Physics losses and data losses are combined to form the total loss. The neural network will try to satisfy both the data and the physical constraints.

By incorporating the laws of physics, PINNs have several advantages. The first is higher data efficiency. By computing the input and output variables, we are creating more data from the original data set to work with, and we have additional information from the physics or PDEs, so the trained model can be more accurate while using less training data. The second is that the method is intuitive and easy to explain since the mathematics are from established laws of physics, which are much less abstract and easier to understand than a pure neural network.

PINNs can be used in a lot of fields where there are established laws that are described in math, like physics, geophysics, biomedicine, etc.

2. Applications of PINN in Various Fields

2.1. Biomedical Engineering

MRI image plays an important role in the medical field, especially in the diagnosis and treatment of cardiovascular diseases. However, traditional MRI image processing methods have some limitations, mainly in terms of low resolution and noise interference. The resolution of MRI images is usually low, which makes it difficult to clearly show the fine structure of blood vessels and complex blood flow patterns, which restricts the accurate reconstruction of vascular structure and hemodynamics. MRI images are susceptible to the interference of various types of noise, such as equipment noise, motion artifacts, physiological noise, etc. These noises will mask the real vascular structure and blood flow information, thus affecting the accuracy of diagnosis. The emergence of physical information neural networks provides a new idea to solve these problems.

PINNs can incorporate the Navier-Stokes equations (partial differential equations describing fluid motion) to construct constrained deep neural networks. Through training, PINNs can learn to remove noise from MRI data and reconstruct clearer and more accurate vascular structures and hemodynamics. PINNs can also construct DNNs constrained by the Navier-Stokes equations to efficiently remove noise from MRI data and perform physically consistent reconstructions, ensuring mass and momentum conservation at arbitrarily high spatial and temporal resolutions[2]. Trained PINN models can also automatically segment arterial wall geometry and infer important biomarkers such as blood pressure and wall shear stress. This information is critical for assessing vascular function and predicting heart disease risk, providing physicians with a more accurate basis for diagnosis and treatment. In the field of tissue engineering, cell growth and tissue development can be predicted by PINNs. PINNs can be used to predict the process of cell growth and tissue development, providing important guidance information for tissue engineering. This helps to develop more effective tissue engineering methods, such as constructing artificial blood vessels and tissue organs. PINN technology brings new opportunities for MRI image processing and is expected to revolutionize the diagnosis and treatment of cardiovascular diseases in the future.

2.2. Geophysics

PINNs are used to solve a wide range of complex geophysical inversion problems. PINNs provide high-resolution information on subsurface structures by tightly integrating with full-waveform inversion, an advanced seismic data processing method. At the same time, PINNs are integrated with simulations of subsurface flow processes and rock physics models that describe how the physical properties of rocks affect seismic wave propagation. Through this integrated application, PINNs can extract key subsurface properties such as rock permeability and porosity from seismic data, which are critical for oil exploration, groundwater management, and other subsurface resource development[3].

The application of PINNs in seismology has also been further extended, especially in combining deep neural networks (DNNs) with numerical partial differential equation (PDE) solvers. This combination allows PINNs to effectively solve a wide range of seismic inversion problems. For example, in velocity estimation, PINNs can provide an accurate velocity structure of the Earth's interior, which is critical for seismic wave propagation simulations and seismic risk analysis. In fault rupture imaging, PINNs help to reveal fault networks and potential rupture zones in the subsurface, which is important for understanding earthquake mechanisms and assessing seismic hazard risks. In addition, seismic localization is another application area that benefits from PINNs. By accurately determining the location of the origin of a seismic event, PINNs help to monitor seismic activity and support seismic early warning systems, and PINNs can extract detailed information about the source of an earthquake over time from seismic records, which is irreplaceable for the study of the dynamics of the earthquake process and the characteristics of the source of the earthquake.

2.3. Revealing Edge Plasma Dynamics through Deep Learning of Partial Observations

Revealing Edge Plasma Dynamics through Deep Learning of Partial Observations Predicting turbulent transport at the edges of magnetic confinement fusion devices is a long-term goal spanning several decades, and currently, there are significant uncertainties in the particle and energy constraints on fusion power plants. PINNs can accurately learn, by only partially observing synthetic plasma, turbulent field dynamics consistent with two-fluid theory for plasma diagnostics and model validation in challenging thermonuclear environments[2].

2.4. Material science

By embedding the laws of physics into the training process of neural networks, an innovative solution is provided to break through the limitations existing in traditional research methods, e.g., in the field of fluid dynamics, where the acquisition of experimental data is often costly and may become infeasible due to technological constraints in some cases. In such cases, PINNs enable accurate predictions of fluid behavior based on limited experimental data and known physical laws. This embedding of physical knowledge not only significantly enhances the generalization ability of the model, enabling the model to maintain high predictive performance on new and unseen data, but is also particularly suitable for data-scarce environments and can improve the predictive accuracy and reliability of the model with limited samples[4]. In the application of stress analysis, PINNs provide a powerful tool for engineers and researchers by simulating the stress distribution of a material when subjected to external forces. This approach not only predicts the response of materials under complex loading conditions but also optimizes the design process and reduces reliance on physical experimentation, resulting in cost savings and shorter R&D cycles. In addition, PINNs help predict the fracture patterns and processing of materials when subjected to cyclic loading or extreme conditions, which is critical to understanding the fatigue life and reliability of materials[5]. By modeling crack initiation, extension, and eventual fracture, PINNs can provide a scientific basis for material design and improvement, leading to improved material performance and durability.

2.5. Energy

PINNs have skillfully combined the efficient learning capabilities of neural networks with precise descriptions of the laws of physics to transform the field of renewable energy. In the development and utilization of renewable energy, PINNs can accurately predict the geographical distribution of energy sources and provide a scientific basis for the siting and layout of power generation systems such as wind and solar, thereby optimizing the performance of these energy facilities. In addition, PINNs can also simulate and predict the energy demand in different regions and periods, which is important for rationalizing energy production, storage, and distribution and realizing the efficient use of green energy. In the field of petroleum engineering, PINNs can help engineers simulate complex fluid flows in reservoirs, which is crucial for understanding the behavior of reservoirs, predicting the transport paths of hydrocarbons, and optimizing extraction strategies[6]. The simulation of PINNs allows for more effective planning of well locations and selection of extraction methods, thereby improving the efficiency and economics of oil extraction. In addition, the application of PINNs in the field of environmental science provides a new perspective on environmental protection and sustainable development. It can be used to simulate and predict climate change trends, including changes in key climate factors such as temperature, precipitation, wind speed, etc., providing a solid scientific basis for formulating environmental protection policies and responding to climate change. Through the simulation results of PINNs, policymakers can better understand the impact of human activities on the environment and thus take effective measures to reduce environmental pollution, protect natural resources, and promote the construction of an ecological civilization.

3. Current Challenges in PINN Application

3.1. Difficulty in learning high-frequency components

PINNs have difficulty in learning high-frequency functions, which is due to the frequency bias that may occur during the training process of the neural network. High-frequency features usually cause the gradient to become very steep, making it difficult for PINNs to accurately penalize the PDE constraint term. To solve this problem, techniques such as domain decomposition, Fourier features, and multi-scale DNNs can be used to help the network learn the high-frequency components.

3.2. Computational overhead for multi-physics field problems

Learning multiple physics fields at the same time may consume a large number of computational resources[2]. To address this problem, each physical field can be learned individually and then coupled together, or the physical fields can be learned in smaller domains using fine-scale simulation data.

3.3. Non-convexity of the loss function

PINNs usually involve training large neural networks whose loss function usually consists of multiple terms and is, therefore, a highly non-convex optimization problem. During the training process, the terms in the loss function may compete, resulting in an unstable training process with no guarantee of convergence to the global minimum. To solve this problem, more robust neural network architectures and training algorithms need to be developed, such as adaptively modifying the activation function, sampling data points, and residual evaluation points during the training process. Also, loss functions for PINNs are mainly defined in a point-valued manner, which may be effective in some high-dimensional problems but may fail in some special low-dimensional cases, such as the diffusion equation for non-smooth conductivity/permeability.

3.4. Lack of rigorous mathematical analysis

There is a lack of rigorous mathematical analysis to understand the capabilities and limitations of physically constrained neural networks such as PINNs, e.g., the approximation capabilities of neural networks. New theories need to be developed to better understand the training dynamics of PINNs and the stability and convergence of the training process, as well as to analyze the goodness of PDE problems involving random parameters or uncertain initial/boundary conditions.

In the physical sciences and chemistry, full-field data are often required for data-driven modeling, but such data are difficult to obtain experimentally and are computationally resource-intensive. There is a need to develop new methods of data generation and benchmarking to assess the accuracy and speed of learning physical information and to establish meaningful metrics to measure the performance of different methods[7].

3.5. Challenges of new mathematics

New mathematical theories need to be developed to analyze physical information learning models, such as analyzing the convergence of PINNs for solving PDE problems and analyzing the goodness of PDE problems involving random parameters or uncertain initial/boundary conditions.

4. Possible Solutions

In response to the above challenges, researchers have proposed various improvement strategies for PINNs to enhance the model's performance and stability. Causality constraints by adjusting the model's loss function to ensure causality in time-dependent problems, thereby improving the model's stability and predictive accuracy [8]. Hard constraint handling of boundary conditions enables PINNs to more accurately satisfy boundary conditions, thereby enhancing the model's adaptability and convergence [9]. Meta-learning methods can also be applied, allowing the model to perform better in transfer across different physical systems [10]. At last, deep spectral feature aggregation is an improved method for spectral feature aggregation, addressing the issues of PINNs in multiphase fluid modeling and enhancing the predictive accuracy in fluid dynamics problems [11].

5. Numerical Experiment on PINN

To demonstrate the application of Physics-Informed Neural Networks (PINNs) in practical problems, we choose a typical partial differential equation problem—the heat equation. We use PINNs to solve the one-dimensional heat conduction equation.

The one-dimensional heat conduction equation can be expressed as

\( \frac{∂u}{∂t}=α\frac{{∂^{2}}u}{∂{x^{2}}} \)

u(x, t) represents the temperature distribution, x is the spatial coordinate, t is time, and α is the thermal diffusivity coefficient.

To simplify, we set the initial conditions and boundary conditions as follows:

Initial conditions:

\( u(x, 0)=sin⁡(πx) \)

Boundary conditions:

\( u(0, t)=u(1, t)=0 \)

The PINN class uses three hidden layers, each with 20 neurons and the tanh activation function. The pinn_loss calculates the error term of the partial differential equation; initial_condition_loss and boundary_loss compute the losses for the initial and boundary conditions, respectively, to ensure that the model predictions satisfy the physical boundary conditions of the problem. The Adam optimizer is used to minimize the loss function, which combines the losses from the equation, initial conditions, and boundary conditions. After training is complete, predicted values of the temperature distribution are generated, and contour plots of the temperature distribution are created using matplotlib.

In this example, we will optimize PINNs for solving the one-dimensional heat conduction equation through causality constraints and hard boundary condition handling. The compute_loss function introduces a causality_weight, which reduces the influence of time by using an exponential decay function of the time point t. This way, the model will prioritize learning information from earlier time points.In the boundary_loss function, the model is forced to satisfy the zero-temperature requirement at the boundary conditions by selecting a single time point (e.g., t=0).

By incorporating causality constraints and hard boundary conditions, the model's loss function includes both the physical constraints of the partial differential equation and the constraints of the boundary and initial conditions. The final plotted graph represents the variation of temperature distribution u(x,t) concerning time t and space x, which is the numerical solution of the heat conduction equation.

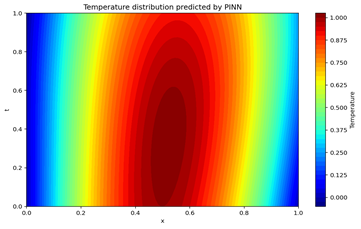
Figure 2: Temperature distribution predicted by PINN without causality and hard constraints.

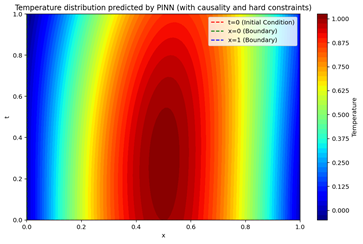
Figure 3: Temperature distribution predicted by PINN with causality and hard constraints.

By incorporating causality constraints and hard boundary condition handling, the model can solve the heat conduction equation more stably. The model converges faster at earlier time points and more accurately satisfies physical conditions at boundary points. This improvement allows the model to better handle boundary conditions and time series data, providing beneficial enhancements for the application of physics-informed neural networks in more complex problems.

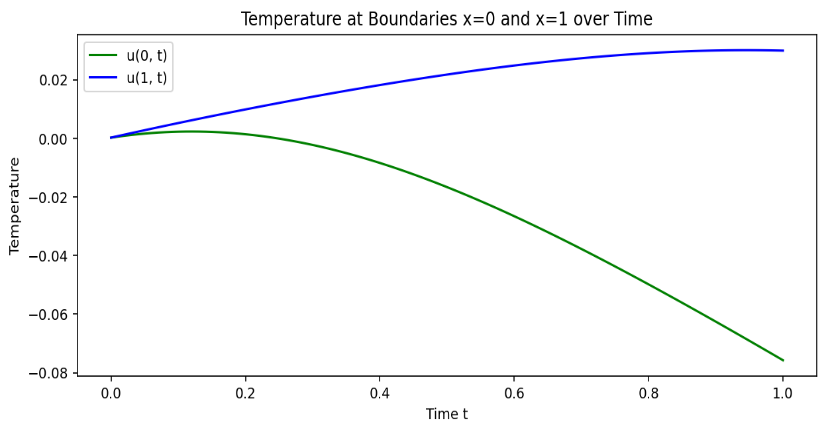
Figure 4: Boundary temperature curve before optimization.

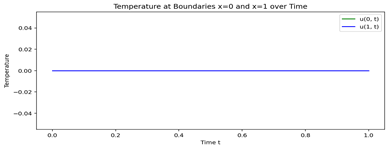
Figure 5: Boundary temperature curve after optimization.

The model before optimization did not adequately adhere to the boundary conditions, exhibiting certain flaws that prevented it from accurately representing the actual situation. In contrast, after optimization, the use of hard boundary condition handling ensured that the model adhered to the boundary conditions, resulting in more accurate predictions.

6. Conclusion

Physics-Informed Neural Networks (PINNs) represent a groundbreaking advancement in bridging the gap between traditional machine learning models and the governing laws of physics. By embedding physical constraints into neural network architectures, PINNs offer unparalleled capabilities in solving partial differential equations and modeling complex physical systems with limited data. This paper has highlighted their diverse applications across various fields, including biomedical engineering, geophysics, material science, and renewable energy. From improving MRI image reconstruction and seismic data interpretation to enhancing stress analysis and energy optimization, PINNs demonstrate their potential to revolutionize scientific and engineering practices.

In conclusion, PINNs offer a transformative approach to integrating physics and machine learning, paving the way for innovative solutions in data-scarce environments. Future efforts should focus on overcoming current challenges, developing more efficient architectures, and expanding their applicability to increasingly complex multi-physics problems. By continuing to refine and expand this technology, PINNs have the potential to unlock new frontiers in scientific discovery and industrial applications.