1. Introduction

In the rapidly evolving digital environment, the need for robust and secure data encryption technology has become critical. As technology continues to advance and adversaries become more computationally powerful, traditional encryption methods face increasing challenges. This has prompted researchers and practitioners to begin exploring alternative encryption methods.

As a highly nonlinear system, neural networks have chaotic complexities within them[1]. Moreover, the inherent nonlinear properties of neural networks, such as unpredictability, randomness and sensitivity to initial values, make them ideal candidates for the development of new encryption algorithms[2]. At the same time, the adaptive and highly fault-tolerant properties possessed by neural networks also facilitate the implementation of cryptography.

The intersection of neural networks and cryptography is one of the key developments in the field of information security. This convergence began in the early 1990s when researchers first explored the possibility of using neural networks for cryptographic purposes. Although research in neural networks and cryptography hit a low point around 1995, in 2002, German scientists Kinzel and Kanter[3,4] implemented a neural network-based public channel key negotiation process using mutual learning synchronization, making the birth of narrow-sense neural cryptography. Kanter and Kinzel's pioneering work on synchronized key exchange in neural networks marks an important milestone in this journey, demonstrating that neural networks can provide new approaches to cryptographic challenges. Subsequently, in recent years there has been a steady stream of completely new neural network models that have been involved in the convergence of the field of cryptography. Currently, there are various neural network models such as Hopfield neural network[5-7], cellular neural network[8-12], convolutional neural network[13,14], adversarial neural network[15,16], etc., which have achieved a large number of results and many iterations in the field of cryptography such as image encryption and cryptographic algorithms.

Despite the growing interest in the intersection of neural networks and cryptography, reviews synthesizing the application and differential analysis of different neural network models in cryptography are still scarce. While several reviews have examined specific aspects of neural cryptography or specific neural network architectures, there is a clear gap in the literature when it comes to analyzing the differences between different neural network models.

The aim of this paper is to analyze the current state of research and applications in the field of encryption based on different neural network models. By examining the strengths, weaknesses and uniqueness of various neural network architectures, this paper will shed light on their application in image encryption and the associated security implications. This paper will begin with an introduction to the fundamentals of neural networks, which will provide a solid foundation for understanding the mechanisms of encryption using neural networks. Then, this paper will explore specific neural network models for encryption, such as chaotic neural networks, cellular neural networks, convolutional neural networks, and adversarial neural networks. For each neural network model, this paper will highlight the unique advantages and potential drawbacks of each approach, and the analysis includes a discussion of the key factors that determine the security and performance of these encryption schemes.

By synthesizing the relevant literature and providing a structured analysis, this review aims to provide a valuable resource for researchers, developers, and policymakers interested in exploring the intersection of neural networks and crypto. The insights gained from this review can inform the design of more secure and efficient cryptographic solutions and provide guidance for future research directions in this rapidly evolving field.

2. Image Encryption Model

The research in this paper focuses on four mainstream neural network image encryption models: chaotic neural networks, convolutional neural networks, cellular neural networks, and generative adversarial networks.

2.1. Chaotic Neural Network (CNN)

Chaotic neural network combines the characteristics of chaos theory and artificial neural network, its chaotic characteristics can generate highly complex and unpredictable pseudo-random sequences, suitable for image encryption in the key generation and perturbation operation, which is most typical of Hopfield neural network, the current mainstream classification:

(1) Chaotic neural network based on weights perturbation: utilizing chaotic sequences to dynamically adjust the neural network weights, making the network state uncertain.

(2) Chaotic neural network based on input perturbation: encryption of images by chaotic mapping of input data.

(3) Hybrid chaotic neural networks: deep fusion of chaotic mapping with neural network models, e.g., embedding chaotic perturbations in convolutional layers.

A typical encryption algorithm framework is shown in Figure 1.

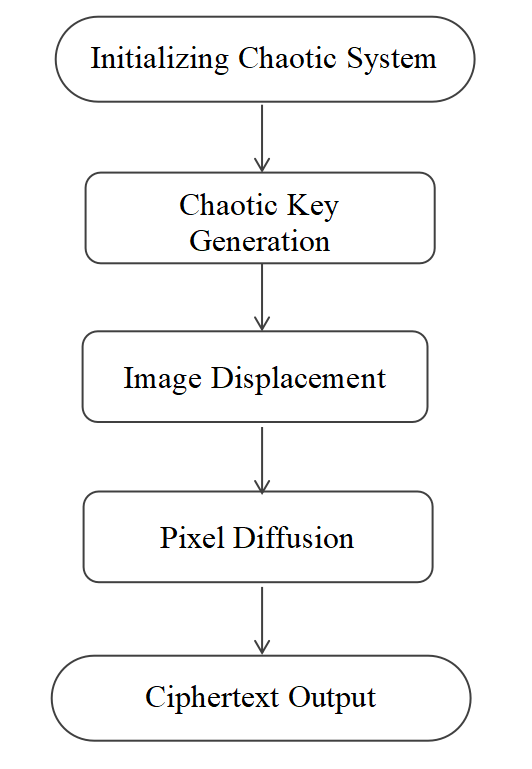
Figure 1: Typical chaotic neural network encryption algorithm (Picture credit: Original)

The initial chaotic system can be based on different chaotic systems to generate initial chaotic sequences, combined with image features to generate dynamic keys, using chaotic sequences to displace the ranks of the image pixels, and finally the chaotic sequences with the original pixel values for element-by-element arithmetic.

2.2. Cellular Neural Networks (CNN)

Cellular neural network is a locally interconnected neural network that can process signals in real time and efficiently, and is suitable for processing image data. The current mainstream classification:

(1) Continuous-Time Cellular Neural Networks: simulating a continuous dynamic system and uses differential equations to describe the evolution of the network state. It is suitable for dynamic encryption processes, such as encryption of real-time image streams, utilizing continuous dynamic characteristics to achieve high complexity encryption operations.

(2) Discrete-Time Cellular Neural Networks: Running at discrete time steps, differential equations are used to describe the update of the network state. It is suitable for encryption of static digital images, with the advantages of efficient computation and simple implementation.

(3) Adaptive Cellular Neural Networks: Network parameters (e.g., template parameters) are dynamically adjusted based on the input image or external key to enhance the randomness and security of encryption.

A typical encryption algorithm framework is shown in Figure 2.

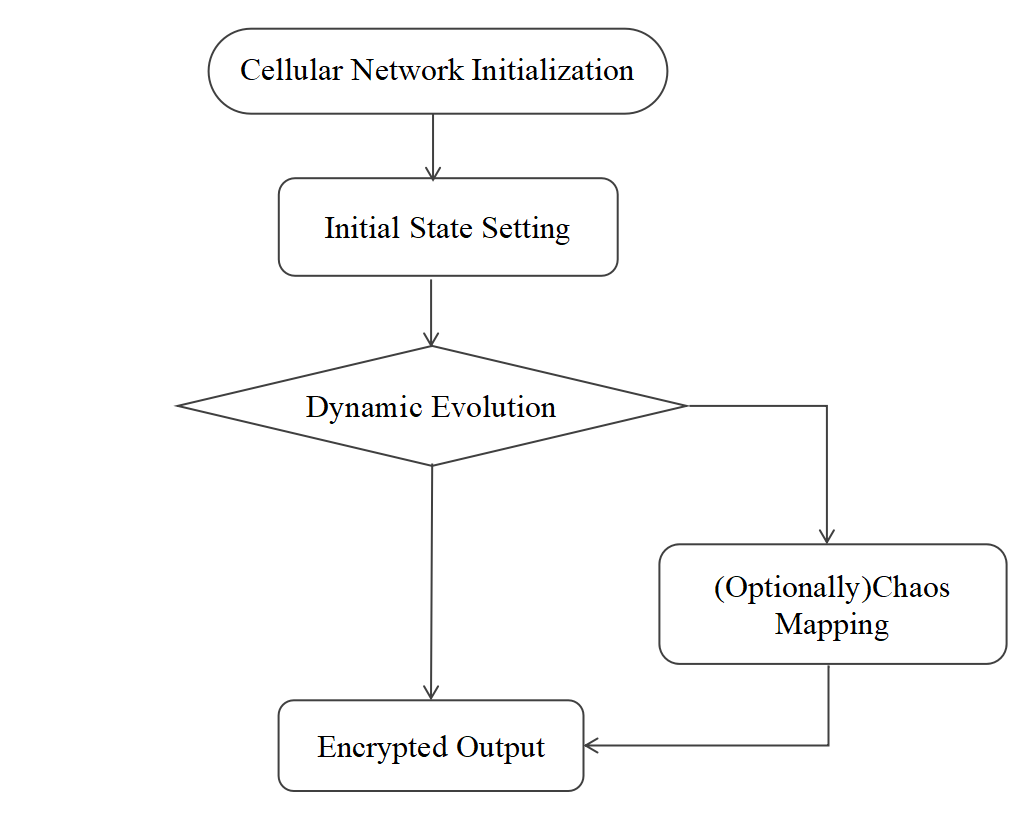
Figure 2: Typical cellular neural network encryption algorithm (Picture credit: Original)

Initially define the cellular network topology and connection templates, take the image pixel values as initial inputs, and iteratively update the cell state according to the CNN dynamic equations.

2.3. Convolutional Neural Network (CNN)

Convolutional neural networks are able to automatically learn and extract features from images through their variable parameter convolution, pooling, and fully-connected layers, focusing primarily on nonlinear mapping and feature extraction capabilities to enhance the complexity and security of cryptographic algorithms. Current mainstream classification:

(1) Single-Layer Convolution Encryption: Basic cryptographic operations on images, such as permutation and diffusion, are implemented through a single convolutional layer.

(2) Multi-Layer Convolution Encryption: The strength and security of image encryption is enhanced by multilayer convolutional operations utilizing the multilevel feature extraction capability of deep CNNs.

(3) Hybrid Convolution Encryption: Combining convolutional neural networks with other cryptographic techniques (e.g., chaotic mapping, traditional encryption algorithms) improves the overall security and complexity of cryptographic systems.

A typical encryption algorithm framework is shown in Figure 3.

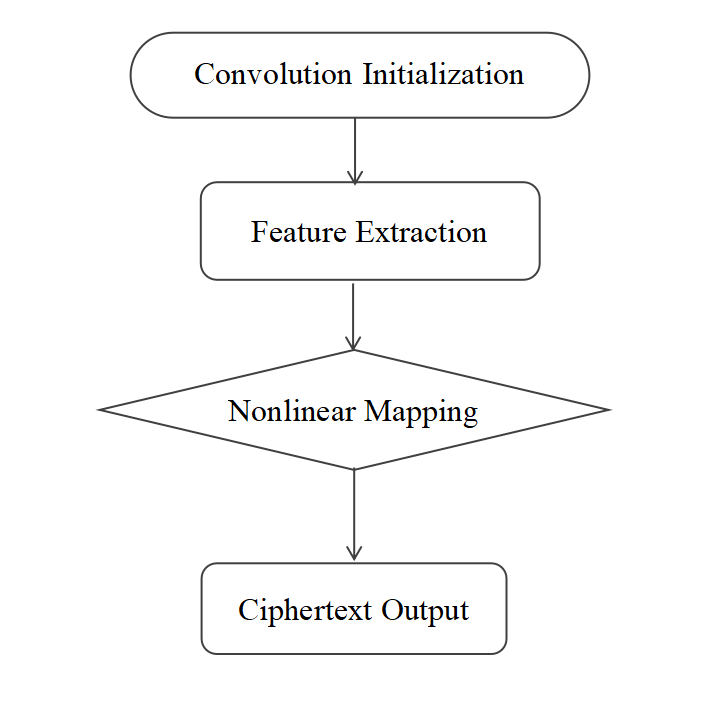
Figure 3: Typical convolutional neural network encryption algorithm (Picture credit: Original)

Construct a convolutional neural system, set the number of convolutional layers, pooling layer and activation function, use the convolutional layer to extract image features and discretize the image, introduce activation function and chaotic mapping for nonlinear encryption of image features.

2.4. Generative Adversarial Networks (GAN)

Generative Adversarial Networks (GANs) provide innovative solutions for image security by being able to generate highly complex and indistinguishable cryptographic patterns through the adversarial game mechanism of generators and discriminators. By learning the data distribution and generating highly random and unpredictable cryptographic mappings, GAN can significantly improve the security of traditional cryptographic algorithms. Especially in areas such as adversarial attacks and image reconstruction, GAN shows unique advantages and potential. Current mainstream classification:

(1) Adversarial Perturbation Encryption GAN: The generator network generates specific perturbation vectors which are confusing and unpredictable. The generated perturbation vectors are superimposed on the original image to form the encrypted image.

(2) Distribution Transformation GAN: The generator maps the original image to the target ciphertext distribution, and the discriminator distinguishes the mapped ciphertext from the true ciphertext.

(3) Direct Ciphertext Generation GAN: The generator network directly outputs the encrypted image, and the discriminator network is responsible for distinguishing the ciphertext from the original image. Through the adversarial training of the generator and the discriminator, a high quality and difficult to restore ciphertext image is generated.

A typical encryption algorithm framework is shown in Figure 4.

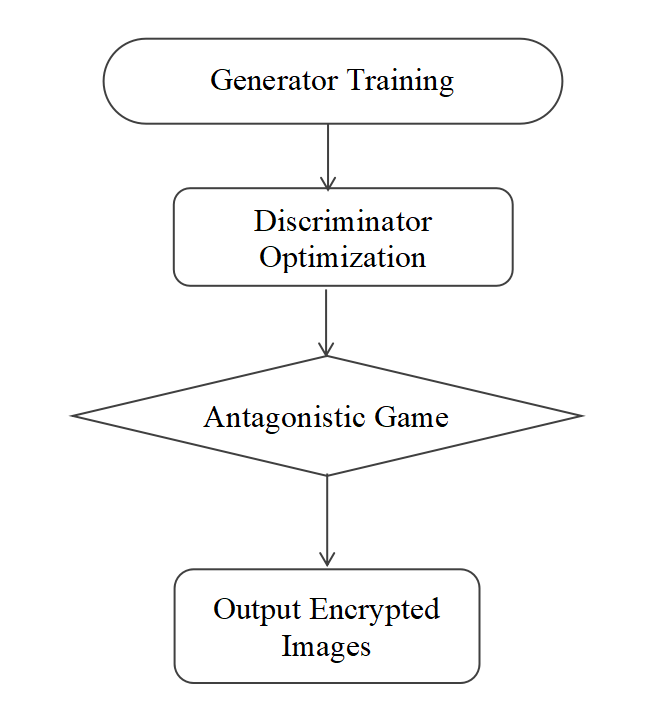
Figure 4: Typical generative neural network encryption algorithm (Picture credit: Original)

Input image \( x \) and random noise \( z \) , generator \( G(z,x) \) generates pseudo-ciphertext, discriminator D(x) evaluates whether the input image is real data or pseudo-ciphertext, by alternately optimizing the generator and the discriminator, the pseudo-ciphertext generated by the generator approximates the ciphertext that cannot be distinguished by the discriminator, and encrypts the input image using the trained generator.

3. Analysis of Variances

In this paper, we compare four neural network encryption algorithms from two aspects, one in terms of cryptographic primitives and the other in terms of encrypted image quality. Cryptographic primitive comparison is mainly based on four aspects: key space size, key sensitivity and neighboring pixel correlation. Cryptographic image quality comparison is mainly based on three aspects: noise resistance of cryptographic images, visual entropy of cryptographic images, and image distortion[17].

3.1. Key Space Analysis

3.1.1. Chaotic Neural Networks

Chaotic neural networks generate keys through chaotic mapping, and commonly used chaotic systems such as Logistic mapping, Henon mapping, and Lorenz system. Due to the special characteristics of chaotic mapping, small changes in the initial conditions and parameters can lead to drastic changes in the trajectory of the system, and this property makes chaotic neural networks have a large key space.

Suppose an \( N \) dimensional chaotic system is used, in which the initial conditions and control parameters of each dimension can be adjusted independently. Then the key space of the whole chaotic system \( K \) can be expressed as:

\( K=\prod _{i=1}^{N}(\frac{{X_{max}}-{X_{min}}}{ΔX})×(\frac{{α_{max}}-{α_{min}}}{Δα}) \) (1)

where \( {X_{min}} \) and \( {X_{max}} \) are the minimum and maximum values of the initial condition, respectively, and \( ΔX \) is the step size of the initial condition; \( {α_{min}} \) and \( {α_{max}} \) are the minimum and maximum values of the control parameter and maximum values of the control parameter, and \( Δα \) is the step size of the control parameter. Due to the high sensitivity of the parameters in chaotic systems, even very small step sizes of \( ΔX \) and \( Δα \) can significantly increase the size of the key space. In addition, literature studies have shown that the key space of a chaotic system is not only related to the dimension of the system, but also closely related to the choice of parameters and the specific realization of the system.

3.1.2. Cellular Neural Network

Cellular Neural Networks key in image encryption depends on initial state, connection weight matrix and input weight matrix. The size of the key space is closely related to the structural complexity of the network (e.g., number of cells, range of connections) and the range of parameters of the weight matrix. The key space consists of an initial state \( {K_{S}} \) , a connection weight matrix \( {K_{W}} \) , an output weight matrix \( {K_{U}} \) .

Suppose there are \( N \) cells in the network, each cell can take \( M \) discrete values, each connection weight \( {w_{ij}} \) can take \( P \) different values, each cell is connected to \( C \) neighbors, the output weight \( {u_{ik}} \) can take Q different values, and each cell receives \( D \) inputs. Combining the above three components, the overall key space \( K \) of the cellular neural network can be expressed as:

\( K={K_{S}}×{K_{W}}×{K_{U}}={M^{N}}×{P^{N×C}}×{Q^{N×D}} \) (2)

Cellular neural network constructs a large key space through multi-dimensional parameters and complex network structure, which significantly improves the security of image encryption system.

3.1.3. Convolutional Neural Network

The encryption mechanism of a convolutional neural network usually relies on the weights (convolutional kernels and biases) of the network. These weights are determined by the training data, so the size of the key space depends on the size of the network, the number of layers, the number of convolutional kernels, and the size of each convolutional kernel.

Assuming that a convolutional neural network has \( L \) layers with \( K \) convolutional kernels per layer, each of size \( m×n \) , the size of the weight matrix is \( W=L×K×m×n \) and the key space can be represented as:

\( S={d^{L×K×m×n}} \) (3)

The weights of a CNN are obtained through a training process and are not randomly generated. In practice, weight values usually follow a specific distribution, which further reduces the effective key space. Compared to chaotic neural networks, their key space is relatively small and may be less resistant to attacks.

3.1.4. Generative Adversarial Network

The size of the key space for generating the adversarial network is related to the dimensionality of the random noise; the higher the dimensionality of the noise, the larger the key space.

Assuming that the GAN employs a \( D \) dimensional random noise vector \( z=[{z_{1}},{z_{2}},…,{z_{D}}] \) and each dimension \( {z_{i}} \) can take \( V \) discrete values, then the key space \( K \) of the whole noise vector can be expressed as:

\( K={V^{D}} \) (4)

The key space of a GAN depends not only on the high dimensionality of the random noise vectors, but also on the complexity of the generator network structure. In addition, GAN optimizes the generator and discriminator through the adversarial training mechanism, which makes the generated encrypted images have higher randomness and complexity.

3.2. Key Sensitivity Analysis

3.2.1. Chaotic Neural Network

Chaotic neural networks are very sensitive to initial conditions and parameters of chaotic systems. Even small changes in the key can lead to drastic changes in the encryption results. This property makes chaotic neural networks highly secure.

Assuming an iterative process \( {x_{n+1}}=f({x_{n}},θ) \) using a chaotic mapping, if \( Δ{x_{0}} \) is a change in the initial value, the error growth after \( N \) iterations can be expressed as:

\( Δ{x_{N}}=f({x_{N-1}},θ)-f({x_{N-1}}+Δ{x_{0}},θ) \) (5)

Initial small deviations are rapidly amplified after many iterations, leading to significant differences in the final encryption results.

3.2.2. Cellular Neural Network

Cellular neural networks exhibit high sensitivity to small changes in the initial state and weight matrix, a property that is amplified by the dynamic evolutionary process of the network.

Assuming that the input image is II, the initial state of the network is \( S(0) \) , the connection weight matrix is \( W \) , and the input weight matrix is \( U \) , the evolution of the cellular neural network can be described as follows:

\( S(t+1)=f(W\cdot S(t)+U\cdot I+B) \) (6)

\( f \) is the activation function. Any small perturbation of the initial conditions or parameters \( ΔS(0) \) , \( ΔW \) , \( ΔU \) will be amplified in subsequent iterations.

3.2.3. Convolutional Neural Network

Convolutional Neural Networks have relatively low key sensitivity in image encryption. Even a small change in the convolutional kernel does not lead to significant changes in the encrypted image. This property is mainly due to the stable weights of CNNs obtained through large-scale data training, which makes them less sensitive to key changes than chaotic neural networks.

Assume that the convolution kernel is \( W \) , the input image is \( I \) , and the convolution operation is \( O=W*I \) . If X, the change in the output is:

\( {O^{ \prime }}=(W+ΔW)*I \) (7)

Due to the training optimization property of convolutional neural networks, small changes in the weights do not significantly affect the final encryption result

3.2.4. Generative Adversarial Network

The key sensitivity of Generative Adversarial Networks in image encryption mainly depends on the dimensionality of its input random noise vectors and the degree of response of the generator to the noisy inputs.

The key is usually represented as an input random noise vector \( z \) , which the generator G maps it to the encrypted image \( G(z) \) . Assuming a small change \( Δz \) in the noise vector, the change in the output image is \( ΔG \) and \( ΔG \) can be expressed as:

\( ΔG=G(z+Δz)-G(z)≈{∇_{z}}G(z)\cdot Δz \) (8)

where \( {∇_{z}}G(z)\cdot Δz \) denotes the gradient of the generator with respect to the noise vector \( z \) . If the gradient change of the generator is small, i.e., \( {∇_{z}}G(z) \) low, it means that a small change in the noise vector will result in a small change in the output image as well.

3.3. Analysis of Neighboring pixel correlation

3.3.1. Chaotic Neural Network

Chaotic neural network can effectively break the correlation between neighboring pixels in an image through chaotic perturbation and pixel disruption operations. In the process of image encryption, the change of pixel values is controlled by chaotic mapping, the relationship between neighboring pixels in the original image is disrupted, and the pixel values in the cipher image are basically uncorrelated.

Assuming that the original image pixel matrix is \( I=[{I_{1}},{I_{2}},…,{I_{n}}] \) , and the encrypted image after chaotic discretization is \( {I^{ \prime }}=[I_{1}^{ \prime },I_{2}^{ \prime },…,I_{n}^{ \prime }] \) , the correlation between neighboring pixels is extremely low. The correlation between pixels is extremely low, \( corr({I_{i}},{I_{j}}) \) is almost zero for neighboring pixels \( i \) and \( j \) .

3.3.2. Cellular Neural Network

The cellular neural network effectively destroys the correlation of neighboring pixels in the original image through a dynamic mechanism of local interaction and feedback between cells. Through the complex dynamic evolution, the local pixel distribution of the original image is nonlinearly perturbed, which makes the correlation between neighboring pixels decrease dramatically.

3.3.3. Convolutional Neural Network

Convolutional Neural Networks are relatively weak in pixel correlation destruction in image encryption. CNNs mainly rely on their convolutional layers to extract image features. The training optimization process of CNNs makes the network weights relatively stable and does not significantly change the correlation of neighboring pixels in encrypted images.

3.3.4. Generative Adversarial Network

The performance of generative adversarial networks in image encryption is between chaotic neural networks and convolutional neural networks. The depth structure of the generator and the nonlinear activation function help to break the correlation between neighboring pixels in the original image. However, GANs have limited sensitivity to random noise. When the generator response to the noisy input is low, it may not be enough to significantly change the pixel correlation of the encrypted image.

3.4. Analysis of Noise Resistance

3.4.1. Chaotic Neural Network

The chaotic system effectively suppresses the propagation of external noise in the encrypted image. This is mainly attributed to the application of chaotic mapping in the encryption process, the process of which can randomize the pixel values of the image to a certain extent, thus making the encrypted image highly resistant to noise.

Suppose that the encrypted image \( {I^{ \prime }} \) is obtained by processing the original image \( I \) and the encryption parameter \( K \) by the chaotic mapping function \( f \) , i.e: \( {I^{ \prime }}=f(I,K) \) . Assume that the response of the chaotic mapping function ff to small perturbations \( ΔI \) and \( ΔK \) of the input image \( I \) and encryption parameter \( K \) is as follows:

\( Δ{I^{ \prime }}=f(I+ΔI,K+ΔK)-f(I,K) \) (9)

Due to the high sensitivity of chaotic systems, the derivatives of the chaotic mapping functions \( \frac{∂f}{∂I} \) and \( \frac{∂f}{∂K} \) show exponential growth under certain conditions, i.e:

\( Δ{I^{ \prime }}≈(\frac{∂f}{∂I}ΔI+\frac{∂f}{∂K}ΔK){e^{λt}} \) (10)

As the number of iterations increases, small perturbations will be magnified exponentially, resulting in significant changes in the overall state of the cipher image.

3.4.2. Cellular Neural Network

Cellular neural networks achieve complex transformations of input images through their local receptive fields and dynamic evolutionary mechanisms, especially in destroying the correlation of neighboring pixels in an image and enhancing the noise resistance of encryption systems, demonstrating significant advantages.

Assuming that the original image \( I \) and the noise \( η \) are encrypted by a cellular neural network, the whole encryption process can be expressed as follows: \( {I^{ \prime }}=CNN(I,η;Θ) \) . \( Θ \) is the set of network parameters, including the connection weight matrix \( W \) and the input weight matrix \( U \) . Combined with equation 6, the state update for each iteration can be described as:

\( ΔS(t+1)={f^{ \prime }}(W\cdot S(t)+U\cdot I+B)\cdot (W\cdot ΔS(t)+ΔW\cdot S(t)+ΔU\cdot I) \) (11)

Cellular neural networks can effectively break the correlation between neighboring pixels in an image through chaotic perturbation and pixel disambiguation operations, which significantly improves the noise immunity and overall security of the encryption system.

3.4.3. Convolutional Neural Network.

Convolutional neural networks may be more affected by noise during image encryption, especially in shallow layers of convolutional neural networks. Because the convolutional operation is based on local perception, it may not be as effective against the expansion of noise as the chaotic neural network.

If the input image contains noise \( η \) , the encrypted image \( {I^{ \prime }} \) can be expressed as:

\( {I^{ \prime }}=W*(I+η) \) (12)

In practice, shallow convolutional neural networks are more sensitive to input noise.

3.4.4. Generative Adversarial Network

Generative Adversarial Networks show some resistance to noise in the image encryption process. However, in practice, noise may still introduce some bias in the training process, especially if the network is not adequately trained or the training data is not sufficient.

Combined with Eq. 8, if the noise \( η \) has less effect on the output of the generator, i.e., the generator's gradient change to the noisy input is low, then the effect of the noise \( η \) on the encrypted image \( {I^{ \prime }} \prime \) is also low

3.5. Analysis of Visual Entropy

The visual entropy \( H({I^{ \prime }}) \) can be calculated from the distribution of gray values of the image:

\( H({I^{ \prime }})=-\sum _{i=0}^{255}p(i)log⁡p(i) \) (13)

where \( p(k) \) denotes the probability that a pixel with a gray value of \( k \) in the image.

Chaotic Neural Networks (CNNs) are able to significantly increase the visual entropy of encrypted images through their stochastic nonlinear mapping.

Cellular neural networks utilize their highly sensitive network parameters and nonlinear dynamic evolutionary processes to significantly enhance visual entropy.

Convolutional neural networks have a relatively limited effect on visual entropy enhancement in image encryption, and the linear nature of the convolutional operation and the stability of the weights make the gray scale distribution of the encrypted image less variable.

GAN realizes complex transformations of image features through adversarial training of generators and discriminators, thus breaking the gray scale distribution and pixel correlation of images to a certain extent and improving visual entropy.

3.6. Analysis of Image Distortion

Distortion can be measured by calculating the similarity of the images before and after encryption. For example, distortion is measured by the Structural Similarity Index (SSIM):

\( SSIM(I,{I^{ \prime }})=\frac{(2{μ_{I}}{μ_{{I^{ \prime }}}}+{C_{1}})(2{σ_{I,{I^{ \prime }}}}+{C_{2}})}{(μ_{I}^{2}+μ_{{I^{ \prime }}}^{2}+{C_{1}})(σ_{I}^{2}+σ_{{I^{ \prime }}}^{2}+{C_{2}})} \) (14)

where \( {μ_{I}},{μ_{{I^{ \prime }}}} \) denote the mean values of the original image \( I \) and the encrypted image \( {I^{ \prime }} \) , respectively, \( {σ_{I}},{σ_{{I^{ \prime }}}} \) denote their variances, respectively, \( {σ_{I,{I^{ \prime }}}} \) is their covariance, \( {C_{1}},{C_{2}} \) are constants.

Chaotic neural networks usually introduce large distortions. The “chaotic” nature of chaotic systems ensures that the correlation between neighboring pixels in an encrypted image \( corr(I_{i}^{ \prime },I_{j}^{ \prime }) \) is almost zero, which usually leads to a significant decrease in SSIM values.

Cellular neural networks are able to perform complex nonlinear transformations of the input image and noise, resulting in higher image distortion.

Since the convolution operation is based on a local perception mechanism that relies on stable weights obtained by optimization during training, the distortion in image encryption is usually low.

The distortion ability of Generative Adversarial Networks in image encryption is between Chaotic Neural Networks and Convolutional Neural Networks. GAN achieves complex transformations of image features through the adversarial training of generators and discriminators, and is able to destroy the correlation between neighboring pixels in an image to some extent.

3.6.1. Tables

Table 1, Table 2 demonstrate a comparison of the characteristics of four neural networks in six domains.

Table 1: Chaotic Neural Network & Convolutional Neural Network.

Table 2: Cellular Neural Network & Generative Adversarial Network.

4. Conclusion

The paper first introduce four neural network models that have been widely used in the field of image encryption, briefly categorize each model and describe their respective algorithmic frameworks. After the theoretical formula research as well as operations, respectively, four common neural network models in cryptography original language and encrypted image quality and other two major areas, six aspects of the comparison, found that the encryption effect of the neural network model to a large extent by the parameters of the model as well as the specific encryption algorithms, on the whole, chaotic neural networks and cellular neural networks are more sensitive to the initial value of the better encryption effects while convolutional neural networks face certain security challenges in encryption effectiveness due to the constraints of weight distribution, dependence on training data, and openness of model architecture; the diversity of generator weights and the dimensionality of noise vectors in generative adversarial networks together determine the overall encryption effectiveness.

The application of neural networks in the field of encryption is booming, more and more models are appearing, and the application of each model in different fields is more refined, and we hope that this paper can provide a little bit of insight and help to researchers in related fields.