1. Introduction

In the world of today, with the development of communication technology and computer technology, the media data in data communication, such as video and audio, are all digitized. A large amount of data resources also greatly burden memory capacity, and broadband channels. Due to technical limitations, many hardware technologies can not meet storage needs, which promotes the research and development of data compression technology theory. Especially with the rise of multimedia technology, the key problem to be solved is the storage, processing, and transmission of a large amount of data. Data compression technology can effectively solve this problem, which makes the research of data compression technology receive more and more attention. Data compression originated in information theory in the 1940s. The main purpose of data compression is to store and transmit information data in compressed form. The theoretical limit of data compression is information entropy [1]. Before 1977, data compression was mainly a part of information theory. With the development of computer technology, the research of data compression algorithms has been extended to the fields of image processing, speech processing, and so on. It is no longer limited to source coding in information theory.

In 1997, Jacob Ziv and Abraham Lempel proposed a new compression method -- LZ77 in the paper ‘A Universal Algorithm for Sequential Data Compression’ [2]. In 1978, they also published the article ‘Compression of Individual Sequences via variable-rate Coding’ [3] and proposed an improved algorithm of LZ77 -- LZ78, which brought data compression research into a new stage. In 1984, Terry Weleh improved the LZ78 algorithm and gave an implementation method called the LZW algorithm [4]. Current commonly used compression tools such as Winzip are based on these compression algorithms.

The research on data compression technology is still the focus of current researchers, and the pursuit of better compression technology has always been their goal. In 2019, B Han et al. put forward an upgraded LZW prefix coding scheme based on azimuth information [5], which is used to solve the problems caused by high acquisition speed, low data transmission bandwidth and limited hardware resources. Likely, when using uniform probability distribution sampling points to compress digital signals, the compression rate may not be high or the acquisition speed may not match. The compression ratio can be raised by 26.25% using the improved algorithm without increasing the hardware storage space and complexity. In addition, the application of data compression algorithms in various fields has also been greatly developed. In 2019, C Liu and Q Liu proposed a convolutional neural network compression method based on LZW encoding [6]. This method is used to solve the problem that the Convolutional Neural Network(CNN) parameters are large and difficult to be transplanted to the embedded platform. After pruning and quantification, the compression ratio of LZW encoding can reach 25. 338. In 2020, ZJ Ahmed and LE George proposed an efficient compression system employing transform coding and LZW compression technique [7]. This system plays an significant role in reducing the amount of data in image compression. The compression results shows that the compression ratio has been improved and the fidelity is acceptable.

Source coding, or data compression, aims to make each symbol transmitted over the channel carry as much information as possible; The goal of channel coding or error control is to make each symbol as few errors as possible. Shannon’s source-channel separation theory [8] points out that source coding and channel coding can be implemented independently without affecting the system’s overall performance. However, this theory assumes that the coding complexity of source coding and channel coding is infinite, under which the tiny bit error rate can be obtained. In fact, this assumption does not work. If the channel bit error is large, the total output and input may have a large error. Therefore, the error resiliency of data compression algorithm is very important. Especially in the fields with special communication channels such as satellite communication and military communication, the ability to resist channel error is very critical.

Currently, most images and videos are encoded by run-length and entropy coding to improve compression efficiency (mainly Huffman coding). In the process of noisy channel transmission, variable length codes are prone to bit errors. However, if the fixed length code is used, it is difficult to obtain high efficiency in some environments. Therefore, improving the ability to resist channel error is also needed to improve efficiency.

In 2013, Yin Kai optimized some coding algorithm according to the error distribution law of different channel conditions and proposed a joint source/channel coding and decoding method in the paper’Technology of Error Detection&Correction Coding and Decoding in Satellite Image Lossless Compression’ [9]. In 2019, to solve the problem of packet loss in video transmission and improve the error resilience of encoded video, M Kazemi et al. proposed an intra coding scheme to obtain the best rate-distortion performance in the paper’Intra Coding Strategy for Video Error Resiliency: Behavioral Analysis’ [10]. This coding scheme has higher coding bit rates and loss than other intra-coding schemes.

This paper aims to study data compression techniques and common lossless data compression algorithms. The structure of the research is divided into three parts. The first part gives an overview of data compression technology, including its classification and performance indicators. In the second part, two lossless compression algorithms -- Huffman coding as well as Arithmetic coding are studied deeply. At first, the basic principle of Huffman coding is introduced, which leads to the error resiliency problem of Huffman coding. The bidirectional decoder is theoretically explored and experimentally analyzed. Secondly, Arithmetic coding is introduced. The principle of this algorithm is analyzed, and the common ways to resist channel error are summarized. The third part summarizes the thesis and explores the future research direction.

2. Overview of data compression technology

Data compression is a technical method to reduce the amount of data and storage space, and improve the storage, processing efficiency and transmission technology without losing useful information [11]. Data compression was originally an important topic in information theory, where it is called source coding. However, in recent years, data compression is not limited to the research and discussion of coding methods, and has gradually formed a relatively independent system. It mainly studies the methods of data representation, transmission, and transformation, intending to reduce the storage space that data takes up and the time needed for transmission [12].

2.1. Data compression classification

Data compression includes two kinds of compression: lossy and lossless. (1) Lossy compression refers to the reconstruction of compressed data, which is greatly different from the original data, but the way of data expression information is not affected. This algorithm is highly efficient in compression [13]. Lossy compression is mostly used for speech, image, and video compression. (2) Lossless data compression is the reconstruction of the used data. Data after reconstructing is the same as the original data, mainly used for text files, databases, special image data and other similar compressed data. This paper mainly studies lossless data compression.

2.2. Performance indicators of data compression technology

Data compression, in general, is a technique that uses the least number of digits to represent a signal. Data compression methods are mainly measured by compression ratio (compression efficiency), complexity, and anti-channel error capability. The entropy of data before and after compression is compared to determine the compression ratio in information theory. Today, however, there is another way to define the compression ratio: the ratio of the data after compression to the original data. The complexity of a signal compression system refers to the amount of hardware equipment needed to implement the encoding and decoding algorithm. The selection of a data compression algorithm is an important factor. Different algorithms have different complexity in different scenarios. At present, the error resiliency ability of the compression system has become an important index to evaluate the compression system, which is of great significance to overcome bad channel conditions and resist interference.

3. Research on basic lossless compression algorithm and its error resiliency

3.1. Huffman coding

Huffman coding is proposed by David Huffman in 1952. It is a general data compression method, which is the basis of most general compression programs. And it is often used as a step in the compression process. Huffman coding has high efficiency, fast operation speed and flexible implementation. At present, the algorithm has formed the core of today’s compression software [14].

3.1.1. Basic principle. Huffman coding is a statistical compression method. The central idea of this method is to encode symbols according to the probability of occurrence of source data [15] . The basic principle is to construct Huffman trees according to the frequency of character occurrence and use Huffman trees for encoding. The higher the frequency of the value, the shorter the corresponding binary encoding length; The less frequent the value, the longer the binary encoding length. So as far as possible, use fewer symbols to represent the data, to achieve compression effect.

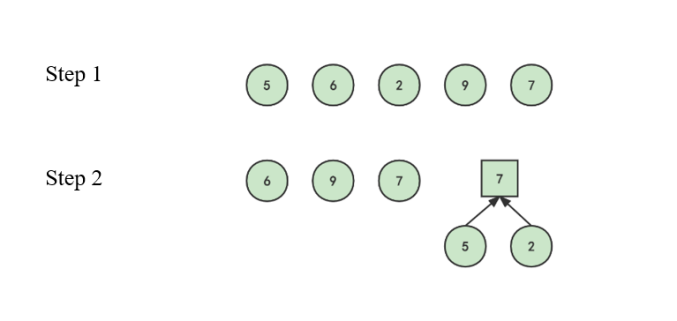
This paper illustrates the specific coding process of Huffman coding through examples. Input: known \( n=5 \) , weight set \( W=\lbrace 5,6,2,9,7\rbrace \) .

Huffman coding process start with arranging source symbols in descending order by weight, Then add the two symbol weights with the lowest weight value to form a new weight value, and rearrange according to the weight value. As shown in step 1 and step in the Figure 1.

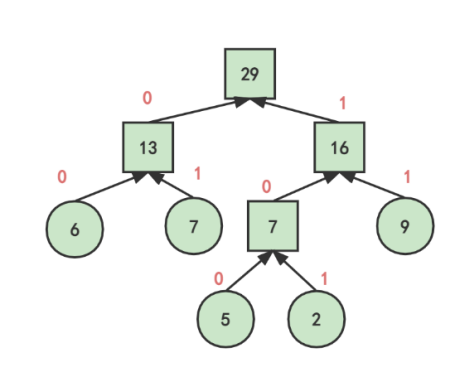
Then, repeat the previous steps until only one weight is left to form a Huffman coding tree. At each pair of merged nodes, the source symbol with high probability is represented by code symbol ‘0’, while the source symbol with low probability is represented by ‘1’. As shown in Figure 3.

Finally, the sequence of ‘0’ or ‘1’ on the branch from the root of the Huffman tree to each leaf node is recorded, so as to obtain the Huffman code of each symbol [16]. As shown in Table 1.

Table 1. The result of Huffman coding.

3.1.2. Research on the error resiliency performance of Huffman Coding

3.1.2.1. Research status of error resiliency in Huffman coding. Huffman coding is a heterologous header code whose correctly transmitted code stream can only be split uniquely [17]. When the bit error occurs, the code segment with bit error and the following code words will have a decoding error. However, due to the unique translatability of Huffman coding, after a few bits, the code-word will be properly re-divided and thus correctly decoded. In other words, Huffman coding does not spread transmission errors. However, for adaptive Huffman coding, when the error occurs, the update of the Huffman codebook at the decoding end may be affected, thus affecting the correct decoding.

Nowadays, there are many pieces of research on the error resistance of Huffman coding. A typical error resistance method, reversible variable length code (RVLCS), is introduced here. The basic idea of reversible variable length codes is that they can be decoded in both forward and reverse directions. Once there is a bit error, even if they jump to the next resynchronization mark in the code stream, reversible variable length codes can still decode the damaged part of the code stream to limit the influence of bit error [18]. For example, Jiangtao Wen and John D. Varasenor introduced a coding scheme that replaces each Golomb-Rice code’s prefixes that begin and ends with ‘1’ and the rest of the prefix is ‘0’. When the prefix length is 1, use 0 to replace it [19]. The suffix and length assignment of RVLCs codes and Golomb-Rice codes are consistent.

3.1.2.2. Bidirectional decodable streams of prefix code-words. This paper introduces a bidirectional decoding method for variable length code (VLC) streams [20]. This method can find the bit error in the code stream, and the coding efficiency is good.

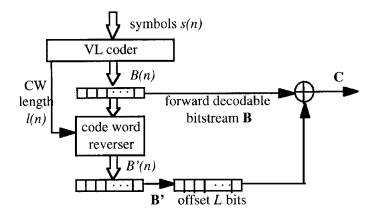
Encoder

Fig. 2 shows the block diagram of the encoder. Divide Symbol \( S(n) \) into several groups and denote by \( B(n) \) , as shown in Formula (1).

The code-word of each code group in \( B(n) \) is flipped and denoted by \( {B^{ \prime }}(n) \) .

\( B=B(1)|B(2)…|B(N) \) \( ={b_{1}}(1)|{b_{2}}(1)|{b_{3}}(1)|…|{b_{1}}(n)|{b_{2}}(n)|…|{b_{l(N)-1}}(N)|{b_{l(N)}}(N)\ \ \ (1) \)

The code-word of each code group in \( B(n) \) is flipped and denoted by \( {B^{ \prime }}(n) \) .

\( {B^{ \prime }}(n)={b_{l(n)}}(n)|{b_{l(n)-1}}(n)|…|{b_{2}}(n)|{b_{1}}(n)\ \ \ (2) \)

As shown in the encoder block diagram, add 0 of \( L \) length after \( B(n) \) , and add 0 of \( L \) length before \( {B^{ \prime }}(n) \) , and perform bit by bit XOR operation on the two groups of code streams to obtain \( C \) , as shown in Formula (4).

\( C=(B(1)|B(2)|…|B(N)|0|…|0) ⊕ (0|…|0|{B^{ \prime }}(1)|{B^{ \prime }}(2)|…|{B^{ \prime }}(N))\ \ \ (3) \)

Since it is bidirectional decoding, the offset needs to meet:

\( L≥{l_{max}}=\underset{n}{max}{l(n)}\ \ \ (4) \)

Decoding in forward direction

Figure 3 shows the block diagram of the decoder. The output of the forward decoder is as follows:

\( (B(n)000…00)=C⊕ (000..00{B^{ \prime }}(n))\ \ \ (5) \)

It can be seen from the above equation, that the last \( L \) bits of \( B \prime \) are the same as the last \( L \) bits of \( C \) . The last L bits of the forward decoding stream are all 0. So the last \( L \) bits of \( C \) are redundant for decoding in the forward direction. Synchronization can be checked according to these properties. If the last \( L \) bits of decoding is not all 0, it means that synchronization has been lost and bit errors has occurred.

Decoding in Reverse Direction

The same is shown in Figure 3. We can first translate the last code group of \( {B^{ \prime }} \) by the character that the last \( L \) bits of \( C \) and \( {B^{ \prime }} \) are the same. Since each code group of \( {B^{ \prime }} \) is the flip of each code group of \( B \) , and we know the length of \( L \) , we can obtain the code stream B. This decoding process continues until a bit error or the beginning of stream \( C \) is encountered.

3.1.2.3. Experimental analysis. This paper uses experiments to verify the correctness of the method. Use Huffman code to encode these characters, flip them according to the principle of bidirectional decodable streams of prefix code-word, and Table 1 is obtained.

Table 2. Symbol code table.

The resulting Huffman code is \( B(n) \) , and the code stream after flipping is \( {B^{ \prime }}(n) \) . Then the operation of equation (4) is carried out by attaching L-length zeros after \( B(n) \) and L-length zeros before \( {B^{ \prime }}(n) \) , the resulting two sets of code streams are subjected to bit-by-bit XOR operations. The process is shown in Figure 5.

According to the principle of forward decoding and the properties of XOR operation, the transmitted bitstream obtained after XOR can be changed into the original bitstream. This indicates that this encoding method can get the correct bit stream.

If a bit error occurs, assume that the error stream is as follows:

1110101001100100111101011111010100001110100010000111101110000111011010001111100011

In comparing the decoder with the code table, an error is reported if the decoded code does not appear in the table. There is no 11 in the code table, but the decoder will consider it a prefix to the symbol A, translate 110 to A, 10 to I, then translate 111 to T, 110 to A, 10 to I, and continue until the whole code-word has been translated. The trailing 6 bits of decoding is not all 0, which means that synchronization has been lost and bit errors has occurred.This indicates that this encoding method can detect the bit error.

3.2. Arithmetic coding

Like Huffman coding, Arithmetic coding is also a lossless compression coding and entropy coding. As an efficient data compression method, Arithmetic coding is widely used in many fields, such as text, image,audio and so on. It is one of the most efficient statistical entropy coding methods so far.

3.2.1. Basic principle. The basic principle of Arithmetic coding is that the encoded message can be represented as an Interval between the real numbers 0 and 1. The longer the message, the smaller the encoded message is, and the more bits are required to represent that interval. This paper shows the basic principle of arithmetic coding through examples.

Set the input source sequence as:

\( u=({u_{1}},{u_{2}},…,{u_{L}}),{u_{l}}∈ \lbrace 0,1\rbrace \ \ \ (7) \)

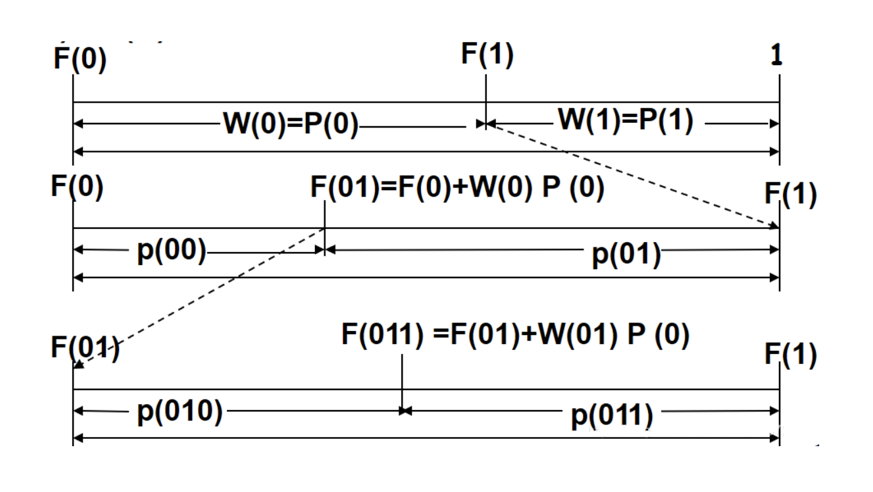
As shown in the figure below, initially, The interval length is \( [0,1) \) . It is divided by \( F(1) \) into two intervals: \( [0,F(1)) \) and \( [F(1),1) \) . The width of the two intervals is \( W(0)=P(0) \) and \( W(1)=P(1) \) , respectively, corresponding to the source symbols 0 and 1. Suppose the first source symbol is 0, and the sequence falls into the interval \( [0,F(1)) \) . Suppose the second source symbol is 1, then the sequence falls into the interval \( [F(0)+W(0)P(0),F(1)) \) . Divide the above interval into two intervals according to probability, the width is \( P(010) \) and \( P(011) \) respectively, and the division line of the interval is \( F(01)+W(01)P(0) \) .

By analogy, the following recurrence relations can be obtained:

\( F({u_{i+1}})=F({u_{i}})+P({u_{i}})F({u_{i+1}})\ \ \ (8) \)

\( W({u_{i+1}})=P({u_{i+1}})=P({u_{i}})P({u_{i+1}})\ \ \ (9) \)

The corresponding interval of the final sequence u is \( [F(u),F(u)+P(u)) \) . Take any value of this interval to get the result of arithmetic coding.

3.2.2. Research on the error resiliency performance of Arithmetic coding. When used with a suitable source model, Arithmetic coding for data compression has been widely accepted as the right method for optimum compression [21]. However, Arithmetic coding is very sensitive to errors [22]. The transmission error of a codeword will affect the decoding of all subsequent codewords, and the error propagation is very serious. The spread of errors is very serious. Therefore, it is very important to study the error resiliency performance of Arithmetic coding.

In order to improve the error resiliency ability of Arithmetic coding, it is a good method to increase redundant data to improve the error detection and correction capability of coding. Source decoding can recover the source symbol according to the compiled binary code. The algorithm uses the automatic synchronization of Arithmetic coding, the knowledge of source statistics and some added redundancy to realize error detection and correction [23].

For example, Boyd et al. [24]proposed two methods to increase redundancy. The first is introducing redundancy by adjusting the coding space so that the encoder never uses some parts. The error will be detected when the number defined by the received encoded string enters the parts that are never used. We call the certain proportion of the current coding interval reduced reduction factor. The reduction factor is used to control redundancy. The second approach is to use a model with two symbols. Encode one of them periodically. When the other is ever decoded, an error occurs.

Chou and Ramchandran [25]placed forbidden symbols to unused code intervals. Then performed Arithmetic coding based on expanded source alphabets. If the forbidden symbol is decoded, there is an error in the transmission.

3.2.3. Comprehensive error detection for Arithmetic coding. The previous paper introduced Boyd’s error detection method by controlling redundancy by controlling reduction factor. Let’s illustrate this approach in detail with an example. This is shown in Figure 5. When the code point falls into the interval \( ({L_{n}},L_{n}^{ \prime }) \) , the interval value is multiplied by a reduction factor R (R between 0 and 1) so that the code point still falls into \( ({L_{n}},{L_{m}}) \) , \( {L_{m}}={L_{n}}+(L_{n}^{ \prime }-{L_{n}})×R \) . The corresponding interval of the code point is reduced, and the interval \( ({L_{m}},L_{n}^{ \prime }) \) becomes redundant. As the coding continues, the redundancy grows. When a bit error occurs during transmission, if a redundant value is transmitted, it indicates a bit error. The smaller the value of R, the faster the redundancy increases and the stronger the error detection performance.

Then select the value of the reduction factor. It can be seen from the above that the growth speed of redundancy and the error detection speed is determined by the reduction factor. First, consider how much redundancy increases by increasing the interval in terms of \( R \) for each bit. If the current interval is of length a, the number of bits to be supplied is \( I(a)=-lo{g_{2}}(a) \) . When the interval is reduced, the number of bits to be provided is \( I(Ra)=I(R)+I(a) \) .

4. Comparison of compression performance between Huffman coding and Arithmetic coding

4.1. Compression performance of Huffman coding

Theoretically, Huffman coding can achieve the best compression effect. However, the actual compression effect often lags behind the theoretical value. This is because information about the Huffman tree must also be stored simultaneously when storing compressed files. This will affect the compression effect. Generally speaking, the impact of the Huffman tree is greater for smaller files and smaller for larger files. At the same time, the compression efficiency of Huffman coding is different for different types of files. The following table shows the results of compression experiments on some files [23].

Table 3. Comparison of compression effects of Huffman coding.

It can be seen from the experimental results in Table 3 that Huffman coding has a good compression effect on bmp files, txt files, wav files, and exe files, and the larger the file, the better the effect.

4.2. Compression performance of Arithmetic coding

Table 4 [23]shows the experimental results of Arithmetic coding for compressing different types of files. It can be seen that the compression effect of Arithmetic coding is different for different file types. Arithmetic coding has a better compression effect on bmp files, txt files, wav files, and exe files, and the larger the file, the better the effect.

Table 4. Comparison of compression effects of Arithmetic coding

Table 4. (continue)

4.3. Comparison of two codes

Huffman coding is a special case of arithmetic coding in essence. But the problem of Huffman coding is that the compression precision is integer bit, while the Arithmetic coding can achieve the compression precision of decimal bit.

Arithmetic coding is more complex to implement, and the compression efficiency is slightly better than that of Huffman. Huffman coding has low implementation complexity (less overhead), and its compression efficiency is slightly lower than that of Arithmetic coding. The common industry practice is optimizing the coding algorithm based on the current Huffman coding to reduce the cost.

The common applications of Huffman coding are JPEG compression coding and AAC, and Arithmetic coding is mostly used in LC3. Table 5 shows the comparison between Hoffman coding and arithmetic coding.

Table 5. Comparison between Huffman coding and Arithmetic coding.

5. Conclusion

With the development of communication and multimedia technology, a large number of data resources put forward higher requirements for compression technology. Data compression technology uses the least amount of data to represent the signal sent by the source to reduce the occupied storage space and improve information transmission rate. The key technology of data compression is excellent coding technology. The capacity to resist channel error is an significant index to reflect the performance of data compression coding. For example, Arithmetic coding with high compression performance has high sensitivity to bit error, which seriously hinders the wide application of Arithmetic coding in wireless multimedia. The quality of wireless multimedia communication can be effectively improved by using certain methods to improve its error-resistant ability. Therefore, it is of great importance to study the error resiliency ability of lossless compression algorithms in common use in communication.

In this paper, the author introduces lossless data compression technology and discusses its basic principle and performance index. The common lossless compression codes are studied, and the main object is their basic principles and error resiliency performance. Huffman coding is the best lossless coding method from the perspective of information entropy. And because of its unique translatability, it can quickly recover from errors. However, the error of adaptive Huffman coding will affect the update of the Huffman coding codebook at the decoding end. This paper introduces the bidirectional decoder with prefixes as a method to solve the bit error. Arithmetic coding has better compression efficiency, but it is very sensitive to error and error propagation is serious. To improve the error resiliency ability of Arithmetic coding, the error detection and correction ability of Arithmetic coding can be improved by adding redundant data.

The next direction of research can be put in the study of lossless compression algorithms in image compression, video compression, and other aspects of the application. In addition, there are still many defects and deficiencies in the research on error resiliency of lossless coding. There should be different characteristics of error resiliency in different applications, which is worthy of further research and practice.