1. Introduction

The prediction of concrete compressive strength is one of the core topics in the field of construction engineering and materials science. As the most widely used building material in the world, the mechanical properties of concrete directly determine the safety, durability and economy of buildings. Traditionally, the determination of compressive strength mainly relies on destructive testing of standard laboratory curing specimens, which is a time-consuming and costly method that takes up to 28 days and is difficult to meet the demand for real-time quality control and construction efficiency in modern engineering [1]. In addition, the strength of concrete is subject to the nonlinear coupling of water-cement ratio, aggregate properties, additive types and curing conditions, etc., and its inner mechanism is complex, so it is difficult for traditional empirical formulas or statistical models to accurately describe the complex relationship between the variables. With the advancement of green building and intelligent construction concepts, how to quickly and non-destructively predict the strength of concrete during the construction phase and reduce the waste of resources through ratio optimization has become a key issue to be solved by the industry. In this context, intelligent prediction methods integrating material science, data analysis and computer technology have gradually become a research hotspot [2].

Machine learning algorithms provide breakthrough solutions for concrete strength prediction. By mining the hidden laws in the historical experimental data, machine learning is able to establish a nonlinear mapping model between the input variables (e.g., cement content, fly ash admixture, age, etc.) and the compressive strength, overcoming the theoretical limitations of the traditional methods [3]. Algorithms such as Random Forest [4] and Support Vector Machine [5] can identify the key influencing factors through feature importance analysis; neural networks, especially deep learning models, exhibit higher prediction accuracy under complex proportioning conditions by virtue of the ability of multilayer nonlinear transformation [6]. In this paper, the kernel limit learning machine is improved based on the vector weighted average algorithm for prediction of compressive strength of concrete.

2. Data set sources and data analysis

We use the open source dataset for experiments, the source of the dataset is kaggle, the dataset contains the content and proportion of the basic components of concrete such as cement, blast furnace slag, fly ash, water, superplasticizers, coarse aggregates, fine aggregates, and age, and the target variable is the compressive strength of concrete, a total of 1,030 pieces of data, this paper selects some of the data to show, as shown in Table 1.

Table 1: Modelling assessment.

It is very important to analyze the relationship between each basic component and the compressive strength of concrete, we use the method of Pearson correlation analysis to calculate the correlation between each cement component and the compressive strength of concrete, calculate the correlation coefficients between them and draw the correlation heat map, as shown in Figure 1, and sorted according to the degree of correlation with concrete, as shown in Figure 2.

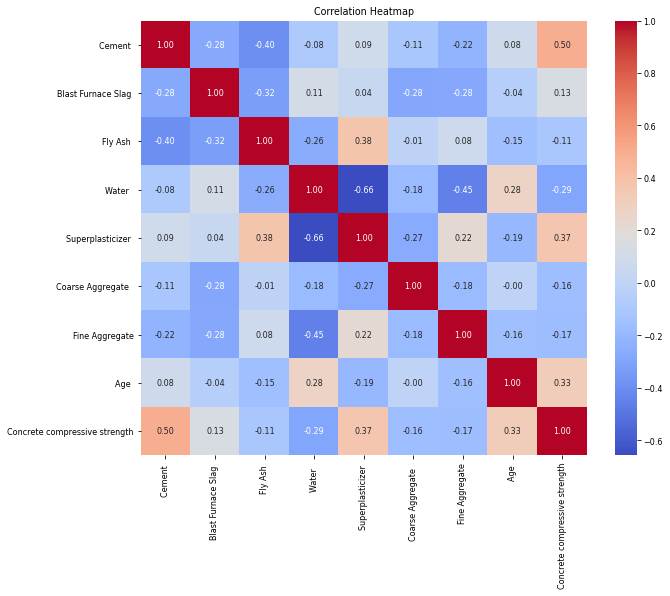
Figure 1: The correlation heat map.

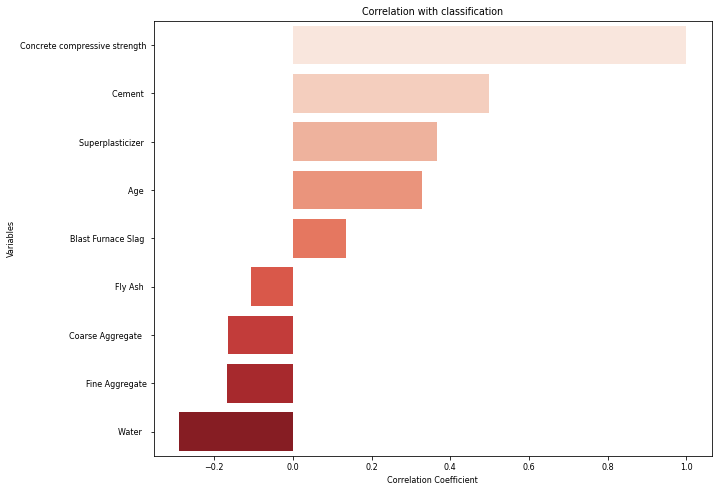
Figure 2: The degree of correlation with concrete.

From the correlation matrix, it can be seen that the most positively correlated variable with the compressive strength of concrete is cement, with a positive correlation coefficient of 0.5; followed by superplasticizer, with a correlation coefficient of 0.37, and age is also an important factor affecting the compressive strength of concrete, with a correlation coefficient of 0.33. It is worth noting that water has a negative correlation with the compressive strength of concrete, with a correlation coefficient of -0.29.

3. Method

3.1. Vector Weighted Average Algorithm

Vector weighted average algorithm is a data fusion method that integrates information from multiple vectors by assigning different weights, and its core idea is to assign specific weight coefficients to each vector according to the difference in importance or reliability of each vector, and then generate the integrated result vector by weighted summation [7]. In the calculation process, each input vector will be multiplied with its corresponding weight, the larger the weight value represents the higher contribution of the vector to the final result, and after all the weighted vectors are superimposed, the sum of the weights is usually normalized to ensure the stability of the result. The key to this algorithm lies in the reasonable setting of the weights, which can either be specified manually based on a priori knowledge or automatically optimized through statistical analysis of data or machine learning models [8]. The pseudo-code of the vector weighted average algorithm is shown in Figure 3.

Figure 3: The pseudo-code of the vector weighted average algorithm.

3.2. Kernel limit learning machine

Kernel Extreme Learning Machine (KELM) is an efficient machine learning model that combines the Extreme Learning Machine (ELM) framework with the kernel method, aiming to improve the generalization ability and stability of traditional ELM through nonlinear mapping, while retaining its fast training characteristics. Traditional ELM avoids the time-consuming gradient descent process in traditional neural networks by randomly initializing the weights of a single hidden-layer neural network and solving the output weights directly analytically, but the randomness of its hidden-layer parameters may lead to fluctuations in the model's performance, and its generalization ability is limited especially under complex data distributions [9].The core improvement of the KELM lies in the introduction of the kernel trick, which implicitly maps the original data to a high-dimensional feature space. thereby bypassing explicit random weight generation and constructing nonlinear decision boundaries directly by measuring the similarity between samples through the kernel function [10]. The schematic diagram of Kernel Extreme Learning Machine (KELM) is shown in Fig. 4.

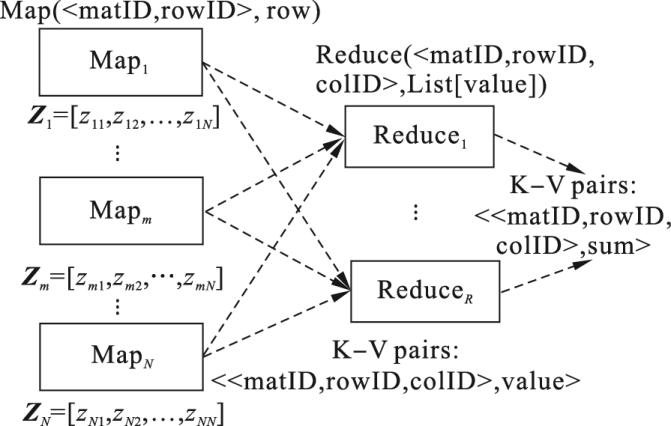
Figure 4: The pseudo-code of the vector weighted average algorithm.

3.3. Kernel limit learning machine optimized for vector weighted average algorithm

The performance of KELM is highly dependent on the selection of the kernel function and its parameters, for example, the bandwidth parameter of the Gaussian kernel determines the degree of local sensitivity of the feature space, which needs to be adjusted according to the characteristics of the data in order to adapt to the nonlinear structure. Compared with the traditional ELM, KELM eliminates the instability caused by the randomness of the hidden layer through kernel mapping, which significantly improves the robustness and consistency of the model, especially in the small-sample or high-dimensional nonlinear tasks.

The algorithm uses a two-level weight update strategy:

1. Sample-level weights: adjusted in real time according to the prediction errors of the samples during training. The samples with wrong prediction will be weighted down to prevent the model from overfitting the local noise; the weights of correctly predicted samples will be gradually increased to strengthen the model's capture of stable patterns.

2. Kernel function level weights: Fusing the outputs of multiple kernel functions (e.g., Gaussian kernel, linear kernel), the weights of different kernels are dynamically adjusted to balance the model's local fitting ability and global generalizability. For example, for data regions with fuzzy boundaries, the algorithm may increase the weight of the Gaussian kernel to capture details; for linearly separable regions, it focuses on the simplicity of the linear kernel.

4. Result

In the experimental setup, the Kernel Extreme Learning Machine (KELM) adopts the radial basis (RBF) kernel function, the regularization parameter C is set to 100 to balance the risk of overfitting, and the kernel parameter gamma is set to 0.1 to control the kernel function bandwidth; the vector weighted averaging algorithm assigns dynamic weights to the training set by calculating the information entropy of the feature vectors in the training set, and the entropy weighting threshold is set to 0.7 to screen the effective features. The dataset was divided into training set and test set according to 7:3, and the optimization parameters were optimized using 5-fold cross-validation; the regression performance was evaluated by mean square error (MSE), mean absolute error (MAE) and coefficient of determination (R²); all experiments were repeated independently for 10 times to take the mean; the data were preprocessed using Z-score standardization to eliminate the effect of magnitude.

The model was introduced for training, and a line graph of the actual values of the training set versus the predicted values of the model was output, with the actual concrete strength in red and the predicted values of our model in blue. The line plot of actual values versus predicted values of the model for the training set is shown in Figure 5, and the line plot of actual values versus predicted values of the model for the test set is shown in Figure 6.

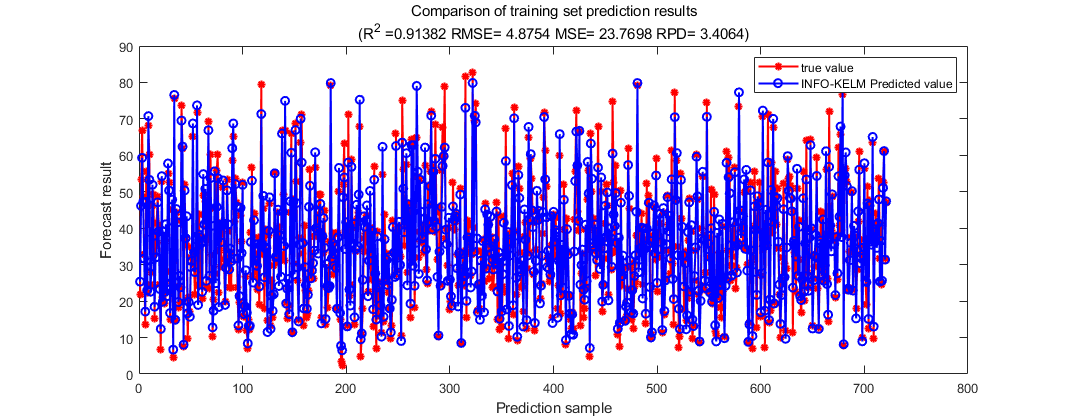
Figure 5: The line plot of actual values versus predicted values of the model for the training set.

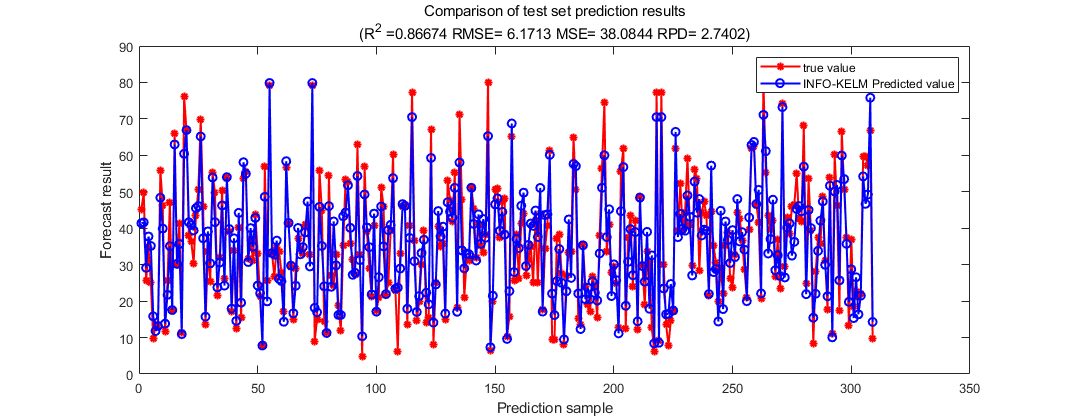
Figure 6: The line plot of actual values versus predicted values of the model for the test set.

From the prediction effect of the training set and test set, our model can predict the concrete compressive strength more accurately from the perspective of quantization.

Secondly, we use the quantitative method to observe more intuitively the prediction ability of our model for concrete strength on the training and test sets. The scatter plot of the actual values of the predicted values in the training set is shown in Fig. 7, and the scatter plot of the actual values of the predicted values in the test set is shown in Fig. 8.

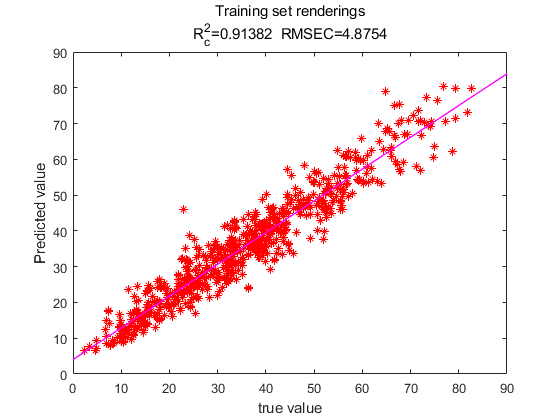
Figure 7: The line plot of actual values versus predicted values of the model for the test set.

Figure 8: The line plot of actual values versus predicted values of the model for the test set.

From the scatter distributions of predicted-actual values in the training and test sets, it is clear that our model is able to predict the concrete compressive strength relatively accurately. From the quantitative point of view, the R2 of the training set is 0.913 and the RMSEC is 4.875, and the R2 of the test set is 0.867 and the RMSEP is 6.171.Among them, the test set is lower than the training set by 0.046 in R2, which indicates that the effect of the test set is reduced compared with the training set, but the value of the reduction is not large, which indicates that the model's ability to generalize is better.

5. Conclusion

This article uses the Newton Raphson algorithm to optimize the XGBoost model and applies it to advertising click prediction tasks. Through the analysis of experimental data, we found that there is a certain correlation between advertising click through rate and multiple variables. Among them, the variable most positively correlated with ad click through rate is ad position, with a correlation coefficient of 0.08; The variable most negatively correlated with ad click through rate is browsing history, with a correlation coefficient of -0.08. These correlation analyses provide important reference for the construction of the model.During the model training process, we observed that the fitness curve of the model showed a significant downward trend, gradually decreasing from the initial 0.184 to 0.148, indicating that the predictive performance of the model continued to improve with the progress of training. This trend further validates the effectiveness of the Newton Raphson algorithm in optimizing the XGBoost model.In addition, this study also reveals the significant impact of advertising location and browsing history on ad click through rates. The position of advertisements is positively correlated with click through rates, indicating that the more prominent the advertisement is on the page, the greater the likelihood of users clicking.