1. Introduction

1.1. Rationale

Disasters including natural or man-made are unavoidable events in human society. In recent years, the frequency and intensity of these disasters have increased. Natural disasters such as floods, storms, tornadoes, wildfires and earthquakes have had a growing impact on densely populated urban areas. Meanwhile, human-made disasters like traffic accidents, industrial accidents and large-scale fires also pose significant threats to human lives [1]. As rapid urbanization and climate change exacerbate the complexity and scale of these events, governments and emergency services face increasing challenges in disaster response.

Fast rescue operations are crucial in disaster situations. According to the studies in the field of Urban Search and Rescue (USAR), the success rate of rescuing trapped individuals is highest within the first 48 hours after a disaster [2]. Beyond this critical time window, the chances of survival for victims decrease sharply, almost reaching zero. Despite deploying essential emergency forces such as firefighters, medical personnel, and police, extreme dangers in disaster areas often put rescuers at great risk.

Conducting manual rescues in unstable debris, toxic environments and unpredictable hazards is not only highly dangerous but also time-consuming. To address these challenges, advancements in robotics provide the possibility to develop search-and-rescue robots [3]. These autonomous machines can effectively replace traditional rescue efforts, reducing the risks to rescuers while completing more efficient and accurate search missions. However, the application of search-and-rescue robots in real disaster scenarios also faces a series of technical challenges, particularly in areas such as environmental sensing, positioning, decision-making and path planning [4]. Among these technologies, the study of path planning algorithms is particularly crucial as it directly determines the robot's ability to autonomously navigate complex environments and complete tasks efficiently. Traditional path planning algorithms, such as the A* algorithm, though working well in known environments, may not meet the requirements for rapid response and adaptability in dynamic or unknown rescue settings [5].

1.2. Research Questions

The efficiency and effectiveness of path planning in search-and-rescue robots have been a focus of research in recent years, particularly in multi-target rescue missions. Robots operating in disaster environments face a number of challenges, including navigating unpredictable terrain, identifying multiple targets, and optimizing paths to maximize rescue efficiency. Thus, the key question this research seeks to address is: How can the efficiency and effectiveness of path planning in multi-target search-and-rescue robots operating in complex environments be improved?

In order to fully answer this question, it is important to consider the sub questions that guide the research: What are the current limitations of traditional path planning algorithms, such as A*, when applied to dynamic, real-world rescue environments?; How can the integration of traditional algorithms like A* and Dijkstra improve real-time adaptability and decision-making in multi-target rescue missions?; How can Simultaneous Localization and Mapping (SLAM) techniques enhance real-time adaptability in complex environments?; What specific improvements can be made to prioritize multiple rescue targets in real-time based on urgency and environmental constraints?

By exploring these sub-questions, the research seeks to develop a comprehensive solution that not only enhances the robot’s ability to navigate complex environments but also improves its efficiency in rescuing multiple targets.

2. Literature Review

2.1. Limitations of Traditional Algorithms

In the field of search-and-rescue robotics, numerous research efforts have focused on improving the efficiency and effectiveness of robots in navigating complex and dynamic environments. The main part of this is the development of algorithms that enable robots to plan optimal paths while accounting for real-time changes and multiple rescue targets. The Dijkstra algorithm, introduced by E. W. Dijkstra, is considered one of the foundational algorithms for finding the shortest path in a network of nodes [6]. This algorithm has served as a starting point for many subsequent path planning solutions due to its reliability in generating optimal paths in static environments. However, its application in dynamic and real-time rescue scenarios reveals certain limitations, particularly when conditions within the environment are subject to rapid change. To overcome the challenges, researchers have sought to extend and refine Dijkstra's algorithm. For instance, Kang, Lee, and Kim proposed an improved version of Dijkstra’s algorithm by integrating it with Particle Swarm Optimization (PSO) [7]. This approach enhances real-time adaptability by optimizing the robot’s path based on dynamic environmental changes, allowing for more efficient navigation during rescue operations. Similarly, Noto also developed an extension of Dijkstra’s algorithm that incorporates advanced strategies in order to efficiently navigate complex environments with multiple obstacles [8].

2.2. Integration of Algorithms

Despite these advancements, Dijkstra’s algorithm continues to face challenges in maintaining real-time adaptability, which has been pushing researchers to explore alternative approaches. One such alternative is the A* algorithm, introduced by Hart, Nilsson, and Raphael. A* builds upon Dijkstra’s work by incorporating a heuristic function that estimates the cost to reach the goal, making it more efficient in larger, more complex environments.[9] While A* has become a popular choice due to its efficiency, it also struggles with handling multiple targets in dynamic rescue missions. To address this, Zhang and Zhao integrated A* with Dijkstra’s algorithm in their study, demonstrating how this combination improved overall pathfinding efficiency in multi-robot rescue scenarios [5]. Their findings highlight the importance of combining traditional algorithms to achieve better coordination with less response time in locating multiple victims during emergencies.

2.3. SLAM Techniques

In addition to advancements in path planning algorithms, the development of Simultaneous Localization and Mapping (SLAM) techniques has significantly contributed to the effectiveness of search-and-rescue robots. SLAM enables robots to map unknown environments while simultaneously determining their own position within those environments, making it a vital tool in disaster scenarios. In their influential work, Grisetti, Kümmerle, Stachniss, and Burgard presented a graph-based SLAM approach that enhances the robot’s ability to handle complex environments [10]. Similarly, Kuswadi, Santoso, Tamara, and Nuh demonstrated the practical application of SLAM in conjunction with the A* algorithm for mobile robots operating in indoor disaster areas, highlighting the effectiveness of this combination in navigating complex environments while avoiding obstacles in real time [11]. This method has proven particularly effective when integrated with algorithms like A*, allowing robots to dynamically adjust their paths in response to newly detected obstacles or targets in real-time. By combining SLAM with advanced path planning techniques, robots are able to have greater autonomy and adaptability, which are crucial for successful completion of rescue missions in unpredictable settings.

2.4. Target Prioritization

Beyond path planning and localization, researchers have also focused on developing strategies for autonomous exploration and target prioritization in rescue missions. Qiu, Chen, Zeng, Xiao, and Zhang investigated target-based exploration strategies specifically designed for search-and-rescue operations [12]. Their study demonstrated that robots equipped with these strategies could dynamically modify their search patterns based on real-time information about the locations and conditions of trapped victims. Similarly, Calisi and Angelelli explored distributed algorithms for autonomous exploration in disaster environments, emphasizing the integration of SLAM technology to optimize area coverage and reduce mission times [13]. This ability to prioritize targets allows robots to drastically improve the speed and efficiency of rescue missions, ensuring that victims in critical condition are rescued first.

The interconnected nature of these studies highlights the importance of combining path planning, localization, and target prioritization to create a comprehensive solution for search-and-rescue robots. By leveraging the strengths of each approach, researchers are paving the way for the development of more efficient, adaptable and ethical robotic systems capable of saving lives in complex and unpredictable disaster environments.

3. Gaps in Understanding

One of the key challenges is the lack of real-time adaptability in traditional path planning algorithms. While algorithms like Dijkstra and A* have shown success in static and predictable environments, their efficiency decreases significantly in dynamic scenarios where conditions change rapidly. Kairanbay and Jani emphasized the need for continuous improvement in the real-time performance of shortest path algorithms to better suit the unpredictable nature of disaster environments [14]. Although multi-objective approaches, such as those proposed by Jin and Razali and Geraghty, show promise, there is still insufficient research on optimizing these algorithms to balance path efficiency and multiple rescue priorities effectively [15,16].

Additionally, while the genetic algorithms have been explored and developed in solving complex optimization problems such as the Traveling Salesman Problem (TSP), there is limited research on applying these algorithms effectively in highly dynamic environments where target locations and obstacles may frequently shift. Razali and Geraghty’s work on selection strategies within genetic algorithms provides a foundation for future research, but there are still rooms to improve the adaptation of these strategies to real-world scenarios with high levels of uncertainty and variability [16]. Addressing these gaps is essential for enhancing the overall effectiveness of search-and-rescue robots in real-world missions, ensuring that they can operate efficiently and reliably in unpredictable and challenging disaster environments.

As the research into search-and-rescue robotics progressed, the initial research question aimed to explore how traditional path planning algorithms could be improved to enhance the efficiency and effectiveness of multi-target rescue missions. While this overarching question remains relevant, the focus has sharpened to address specific challenges in optimizing these traditional algorithms for multi-target path planning in real-world applications. The revised research question focuses on: How can traditional path planning algorithms be improved and integrated to optimize real-time adaptability and target prioritization in multi-target search-and-rescue missions?

4. Methodology

4.1. Common Methods

Research in search-and-rescue robotics relies heavily on a combination of simulation-based testing and real-world experimentation to evaluate the effectiveness of various algorithms and robotic systems. This combined approach aims to better recreate the challenges of real rescue missions, allowing researchers to test and improve various path planning strategies, localization methods, and target detection.

One of the most widely used approaches is the simulation of dynamic environments. Simulation platforms like the Robot Operating System (ROS) allow researchers to create realistic scenarios in which robots must navigate complex terrains, avoid obstacles, and locate multiple targets. A study by Jin introduced a multi-objective A* algorithm in a multi-objective simulation environment, demonstrating how simulations can optimize different path planning objectives simultaneously [17]. Jin’s work highlights the importance of using advanced algorithms in simulated rescue scenarios to enhance robot efficiency and adaptability [17]. Algorithmic integration is also a key focus in the field. Researchers like G. Frare has explored the integration of the Dijkstra algorithm with the Traveling Salesman Problem (TSP) to improve multi-target path planning [18]. Frare’s approach emphasizes the need to combine foundational algorithms with more advanced optimization strategies to handle the complexities of dynamic environments efficiently [18]. Similarly, Chen et al. proposed the SMUG Planner, which focuses on multi-goal planning for mobile robots in challenging environments [19]. Their work underscores the importance of prioritizing safety and goal optimization when testing algorithms in simulated rescue missions.

In addition to simulations, physical testing is also a crucial method for validating the effectiveness of algorithms and robot designs. Kiyani and Khan developed a prototype search-and-rescue robot that was tested in physical environments to assess its real-world performance [20]. This testing allowed them to evaluate the robot’s obstacle avoidance capabilities and adaptability to different types of terrain. Researchers frequently construct maze-like environments using foam boards or other materials to simulate the kinds of challenges that robots are likely to encounter in disaster scenarios. This physical experimentation provides insights into the robot’s ability to perceive and react to unexpected obstacles and dynamically changing target locations.

Data collected from both simulations and physical tests is crucial for the refinement of algorithms and models. Researchers like Colas et al. emphasize the importance of data analysis in 3D path planning and execution for search-and-rescue ground robots [21]. Their approach involves collecting and analyzing quantitative data to refine algorithms continuously and improve the robot’s real-world performance. To measure the effectiveness of integrated systems, metrics such as path efficiency which includes computation time and traveled distance, target prioritization accuracy, and so on are commonly used.

Lastly, the field also incorporates genetic algorithms as a method for solving complex optimization problems in search-and-rescue missions. Studies by Deng, Liu, and Zhou have explored the use of genetic algorithms in solving the symmetric TSP, which is critical for multi-target rescue operations [22]. Razali and Geraghty have similarly analyzed different selection strategies to enhance the performance of genetic algorithms, showcasing their multiple considerations in addressing path planning challenges [16].

4.2. Modified Research Method

Based on the analysis of common methods in this field, the modified research method I have developed consists of three phases: Algorithm Design and Development, Robot Design and Integration, and Experimental Testing and Evaluation. The structuring of these three phases ensures the proper execution of the experiment and the collection of accurate and reliable data.

4.2.1. Algorithm Design and Development

The goal at this phase is to design multiple preliminary improved path planning algorithms, which will be tested in the following simulation tests to identify the optimal performing algorithm. Firstly, I analyzed three classic path planning methods: the Dijkstra algorithm, the A* algorithm, and the Traveling Salesman Problem (TSP) optimization algorithm. The Dijkstra algorithm is a single-source shortest path method based on graph search. It follows a greedy strategy by continuously expanding the node with the smallest cost [23]. While it guarantees an optimal solution, its wide search scope makes it computationally heavy—especially in complex environments, leading to longer calculation times. On the other hand, the A* algorithm builds on Dijkstra by adding a heuristic function (usually based on Manhattan or Euclidean distance) to estimate the cost from the current node to the target [24]. This reduces the search area and improves efficiency. In many cases, especially on large maps, A* runs faster than Dijkstra. However, both algorithms are limited when handling multiple targets because they focus on optimizing a single path without considering the connections between multiple target points. To overcome this, I introduced the TSP optimization algorithm. Its goal is to find the shortest route that visits all target points, thus avoiding unnecessary detours and repeated visits. TSP typically uses the nearest neighbor approach or other optimization strategies to generate a globally optimized route [25]. When combined with Dijkstra or A*, it has the potential to enhance the overall efficiency of multi-target path planning. Therefore, by integrating the A* algorithm, Dijkstra algorithm, TSP algorithm, and Simultaneous Localization and Mapping (SLAM) technology, I plan to develop an algorithm capable of handling multi-target search-and-rescue tasks. This algorithm will not only account for task prioritization but also adapt to dynamic environmental changes.

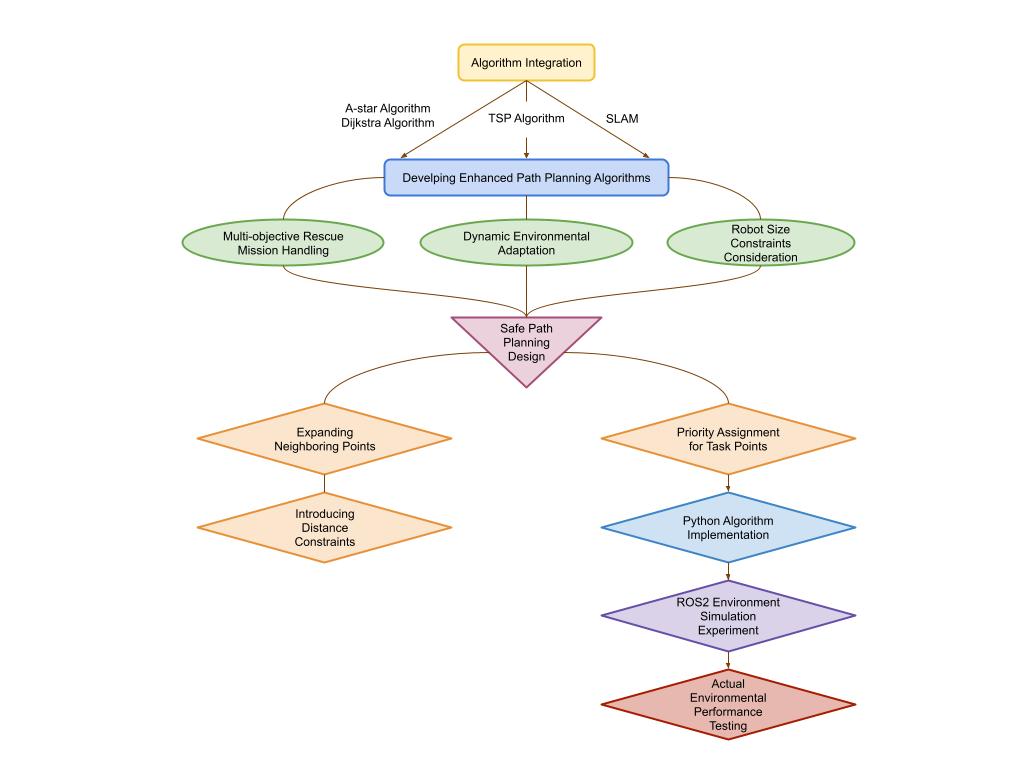
Figure 1: Algorithm Design Flowchart

The Figure 1 above illustrates the thought process of my algorithm design. As illustrated in the flowchart, I have designed two improved algorithms: the A+TSP algorithm and the Dijkstra+TSP algorithm. Based on this, I further consider the robot's physical dimensions and potential obstacles, incorporating a more secure path planning strategy into the algorithm. By expanding neighboring points and introducing distance constraints, the robot can have more choices for its motion direction.

Subsequently, for algorithm implementation and simulation testing, I use PyCharm for coding and simulation to ensure the correctness of the algorithm logic and the feasibility of its implementation. Detailed simulation experiments are conducted in the ROS2 environment under the Ubuntu system to test the algorithm's performances. The simulation experimental setup features a complex virtual maze that mimics the distribution of obstacles and passageways in post-disaster environments. Multiple target points are set up to assess the algorithm’s ability of planning paths in multi-target scenarios. I assign different priority levels to these target points. For instance, green points represent high-priority targets, such as trapped individuals, which the algorithm must visit first. Yellow points indicate lower-priority targets, like valuable items, which the algorithm should try to visit without significantly increasing the overall path cost. This set up better simulates the varying importance of different objectives in real rescue missions. It forces the algorithm not only to find the shortest path but also to balance the priorities of the targets. Finally, based on the results of the simulation tests, I select the best-performing algorithm for subsequent physical validation. Then, I will make necessary debugging and parameter adjustments to further optimize the algorithm. This aims to maximize the performance of the algorithm in complex environments through iterative improvements. The tuning process includes, but is not limited to, adjusting algorithm parameters, optimizing computational efficiency, and improving the accuracy and safety of path planning.

4.2.2. Robot Design and Integration

In the robot design and integration phase, my goal is to develop a robot capable of testing the improved algorithm in physical experiments. I carefully select and integrate various hardware components to meet the algorithm requirements and address the complexity of rescue tasks. Based on a deep understanding of algorithm needs and the complexity of rescue tasks, I select the following components as the robot's core parts (see Fig 2):

- Autonomous intelligent controller for implementing advanced decision-making and executing the path planning algorithm;

- 3irobotix 3i-T1 lidar sensor for high-precision environmental perception and map construction;

- Brushless DC gear motor to provide stable and efficient power output;

- 18650 lithium-ion battery to provide long-duration energy support for the robot.

After selecting suitable components, I proceed with the design and integration of the robot's power system, sensing system, and control system. This aims to achieve robot’s optimal performance by ensuring the compatibility and efficient collaborative work of various systems. Subsequently, integrating the improved path planning algorithm into the robot's control software is another key task of this phase. I need to ensure that the algorithm can seamlessly interact with hardware components, including data collection from sensors and control of the power system, to achieve precise navigation and task execution. Finally, I conduct detailed on-site debugging of the robot to make sure that all systems can work as expected. This step involves adjusting parameters, testing functions, and optimizing performance. The figure below shows the connection setup of the components I designed.

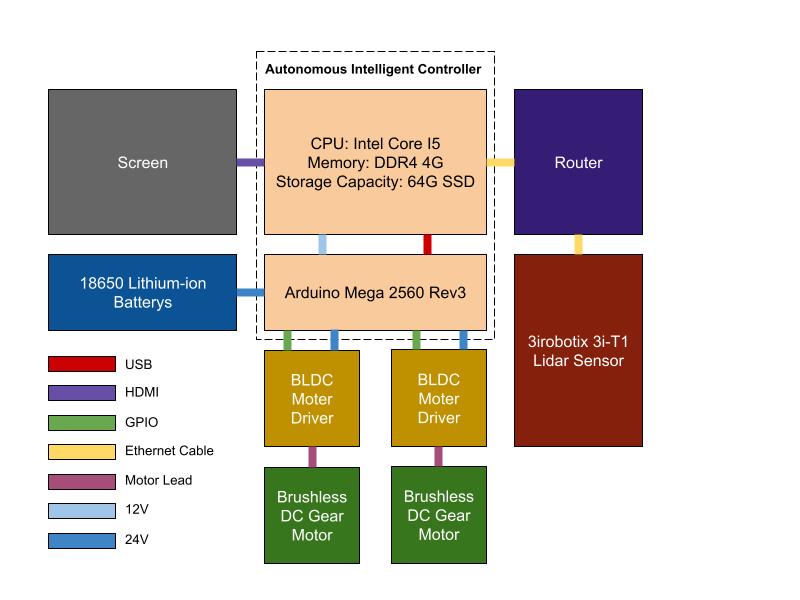
Figure 2: Hardware Connection Diagram

4.2.3. Experimental Testing and Evaluation

In this phase, I create a physical environment to validate the effectiveness and adaptability of the improved algorithms in real-world settings. Unlike the simulated environment, the physical maze experiment better mimics the unpredictable factors that affect a robot's navigation and decision-making in rescue scenarios. This approach allowed me to evaluate the algorithm’s robustness and feasibility under real-world physical conditions.

Firstly, I construct various maze configurations with foam boards in an empty classroom of approximately 10m*8m. These mazes are designed to simulate environments like earthquake rubble or indoor rescue scenes. The mazes include passages and corners of varying widths, and some sections are fitted with additional obstacles to introduce uncertainty. These mazes serve as the basic platform for experiments, used to test the robot's navigation capabilities and task execution efficiency.

The testing plan is conducted in two stages. In the first stage, the robot is placed in the maze, using its sensor system to traverse the maze and construct a planar map of the maze. This step tests the robot's environmental perception and map construction capabilities. After constructing the maze planar map, different task points are marked on the map, and priorities are set for these task points. This step simulates actual rescue mission scenarios, such as areas that need to be prioritized for rescue or locations that require focused search efforts. After setting up the target points, the robot re-enters the maze and executes tasks according to the optimized path planning algorithm. In this stage, the test primarily examined its path planning efficiency, obstacle detection, and the differences between simulation and physical experiments when handling multiple target points. During the experiment, the robot’s path routes, travel distance, and travel time were recorded. If new obstacles appeared, the robot used its LiDAR to update the map in real time and dynamically replan its path, thereby testing its adaptability in an actual setting. The testing also introduces path smoothing techniques by considering the robot's size and potential obstacles. This is able to eliminate unnecessary turns and abrupt path changes, optimizing the robot's trajectory.

5. Data Analysis and Results

5.1. Simulation Results

In the simulation tests, as mentioned in the previous section, I examined the performance of the two improved algorithms under different numbers of target points. I tested Dijkstra, A*, Dijkstra combined with TSP, and A* combined with TSP under scenarios with 1, 2, 4, and 8 target points. For each test, I recorded both the “Path Cost” (the total distance traveled) and the “Time Cost” (the total computation time). Every algorithm was run under the same map conditions, and I documented the generated paths while calculating the path cost and the time cost to evaluate efficiency and stability. Each experiment was repeated several times to ensure the data was reliable and statistically significant. “Path Cost” refers to the total length of the route from the starting point, through all target points, to the final destination. This metric measures how effectively the algorithm plans an optimal path. “Time Cost” is the total time the algorithm takes to compute this path, reflecting its computational efficiency. For search and rescue missions, a lower path cost means the robot can complete the rescue along a shorter route, while a lower time cost indicates that the algorithm provides quicker results—reducing decision delays and improving emergency response.

In the data analysis, I compared the performance of the four algorithms across different numbers of target points by calculating the mean and standard deviation of the metrics I collected.

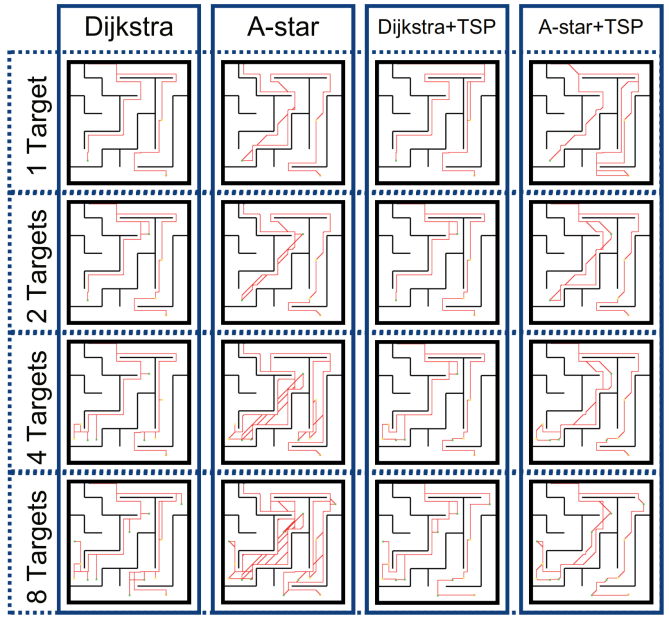
Figure 3: Path Planning Diagrams

The path planning diagrams (Figure 3) illustrated the paths generated by the four algorithms under 1, 2, 4, and 8 target scenarios. With just one target, all algorithms produced similar, direct paths. As the number of targets increased, the paths became much more complex. With two targets, the A* algorithm produced a more compact route compared to Dijkstra. Moreover, both Dijkstra+TSP and A*+TSP showed obvious improvements by minimizing unnecessary detours. When there were four targets, the paths from Dijkstra and A* started to show some backtracking, resulting in longer routes. In contrast, the combined methods provided more systematic paths with a better sequence of visits, reducing redundant travel. In the case of eight targets, the paths generated by Dijkstra and A* became quite redundant, whereas Dijkstra+TSP and A*+TSP achieved significantly shorter and more compact routes—demonstrating the clear advantage of TSP optimization when many targets are involved.

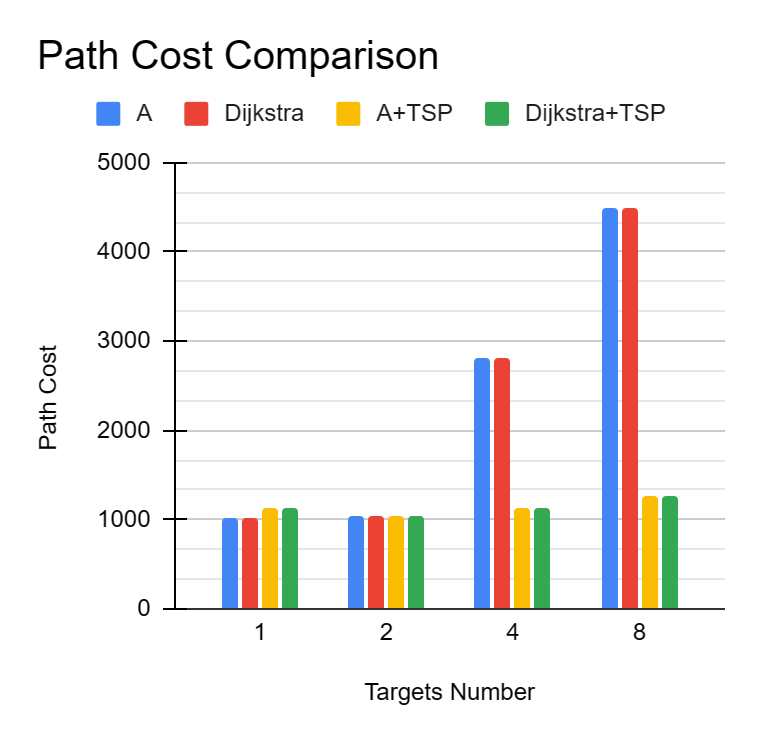
Figure 4: Path Cost Bar Chart

The bar chart (Figure 4) presented the “Path Cost” for each algorithm. With 1–2 targets, all algorithms maintained a similar cost, ranging between 1000 and 1200. This suggests that TSP optimization did not have a significant effect when the target count was low. However, with 4 targets, the path costs for Dijkstra and A* jumped to nearly 3000, while the costs for Dijkstra+TSP and A*+TSP remained much lower. With 8 targets, the path cost for Dijkstra and A* approached nearly 5000, but for the combined methods, it dropped to around 1300—a reduction of about 60%. This clearly indicates that TSP optimization greatly reduces the total path length in scenarios with many targets, especially when integrated with A*.

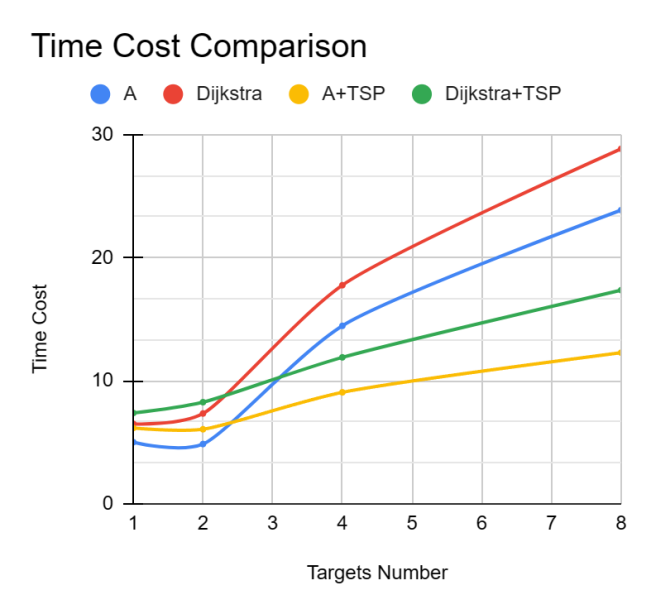
Figure 5: Time Cost Line Chart

The line chart (Figure 5) depicted the “Time Cost” for the algorithms. With 1–2 targets, A* had the shortest computation time, followed by Dijkstra. Since TSP optimization adds extra steps, its computation time was slightly higher when there were fewer targets. With 4 targets, Dijkstra’s computation time surged to around 18 units, while A* took slightly less time. With 8 targets, Dijkstra’s time rose sharply nearly 30 units, whereas A* took about 23 units. In comparison, Dijkstra+TSP and A*+TSP maintained more controlled times, roughly 17 and 12 units respectively. Notably, A*+TSP not only optimized the path but also delivered the best computational efficiency.

The results above showed that while the A* algorithm usually had a faster computation time than Dijkstra, Dijkstra often produced a more optimal path. However, when TSP was integrated, the dynamics changed. With fewer target points, TSP sometimes added extra computational overhead, increasing both the path length and task time. In contrast, when there were many target points, the A*+TSP algorithm can significantly reduce path cost and enhance overall efficiency.

Overall, the improved A*+TSP algorithm demonstrated the best performance in multi-target rescue missions. It showed superior path optimization, lower path costs, and reduced computation time, particularly when a large number of target points were involved. Although TSP optimization may introduce extra computation when target numbers are low, it benefits in complex, multi-target environments. It significantly reduces redundant paths and enhances overall path planning, enabling the robot to visit more targets in less time within effective search and rescue operations.

5.2. Physical Environment Test Results

According to my research plan, after completing the simulation experiments and carrying out initial validations of the algorithm, I further tested the improved algorithm (A*+TSP) in a physical maze environment to assess its effectiveness and adaptability in real-world settings.

Figure 6: Testing Robot

According to my robot design, the testing robot’s hardware platform combined an autonomous intelligent controller, a 3irobotix 3i-T1 LiDAR sensor, and a brushless DC motor drive system, all powered by 18650 lithium batteries (shown in Figure 6). This setup allowed the robot to explore and navigate the mazes successfully. In the beginning, the robot successfully scanned the empty maze using only its LiDAR and odometer and created an initial 2D map. This proved the mapping accuracy and stability of the SLAM system in the physical environment.

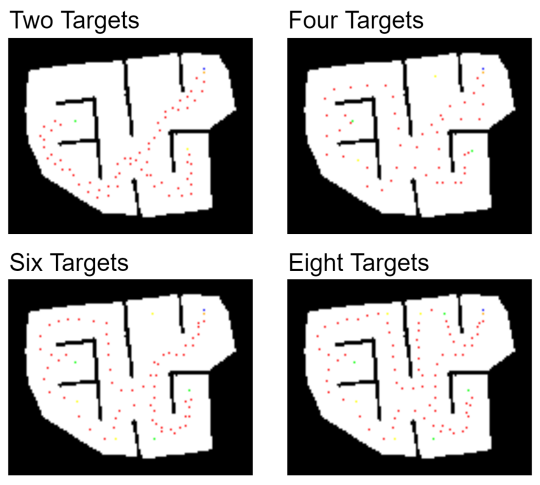
Figure 7: Path Planning Diagrams

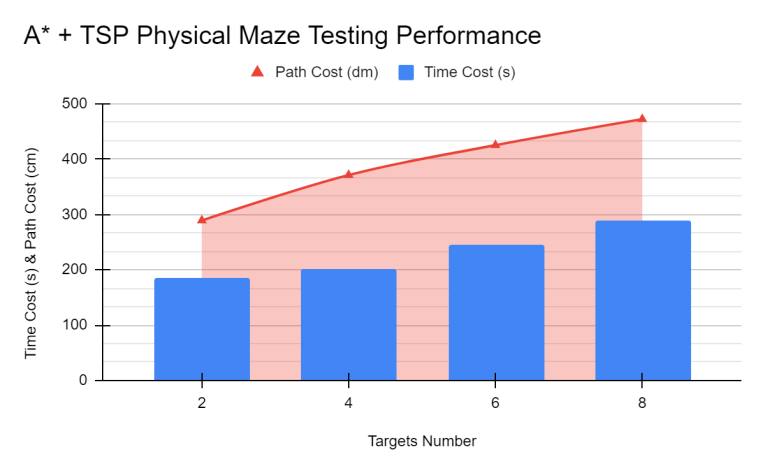
Figure 8: Path Cost & Time Cost Line Chart

The robot entered the maze for the second time. When 2, 4, 6, or 8 target points were marked, the A+TSP algorithm was activated, successfully planning and executing the multi-target path. The path planning diagrams (Figure 6) and the data chart (Figure 7) for different numbers of targets indicate that in scenarios with fewer targets (2–4), the robot’s overall travel distance and completion time were relatively low. This suggests that when there are fewer targets, the A*+TSP algorithm can quickly complete multi-point navigation. As the number of targets increased to 6 or 8, the path coverage expanded significantly, leading to longer travel distances and increased time. Nevertheless, with priority management in place, the robot still visited all target points in the predetermined order efficiently. In the physical environment, obstacles that could not be completely modeled in advance sometimes disrupted the planned route, causing detours or temporary slowdowns. However, thanks to the combined effect of the improved algorithm and SLAM, the robot was able to quickly adjust its path upon detecting new obstacles, without any significant stalling or excessive re-searching. It is worth noting that factors such as sensor noise and ground friction tend to be more pronounced in narrow passages or sharp turns, occasionally causing minor delays in obstacle avoidance. Overall, though, the robot maintained a generally smooth and continuous pace.

During the testing process, I paid special attention to the impact of path smoothing and maneuverability. In the physical environment, the constraints imposed by real-world dimensions are more evident. Without path smoothing techniques, the robot might end up starting and stopping frequently during turns or obstacle avoidance, or even become stuck in corners. To address this, I introduced a path smoothing technique to the algorithm to reduce the impact of sharp turns and cumulative errors. The experimental results confirmed that this improvement effectively lowered the risk of collisions and enhanced route continuity. However, it is also important to note that overly smooth paths may increase the distance needed for path adjustments at complex corners, slightly raising the time for certain segments. This effect was not apparent in the simulation but became a factor in the physical tests. Although the absolute values differed between the physical experiments and the simulations, the overall trends were consistent, demonstrating that the algorithm’s performance in real conditions generally followed the patterns observed in simulation.

Based on the experimental observations and data analysis, it is clear that the A*+TSP algorithm still maintains relatively stable and efficient navigation capabilities in a physical maze for multi-target rescue missions. Although both the path length and time increase as the number of targets grows, the data trend tends to flat through priority management and dynamic replanning, indicating that the algorithm still effectively maintains search efficiency—a conclusion that aligns with the simulation results. One key difference is that the physical environment introduces additional interferences such as sensor noise and mechanical friction, which diversify the sources of error. This suggests that further optimizations in path smoothing and motion control strategies are necessary. Overall, the physical maze experiment confirmed the feasibility and effectiveness of the improved algorithm and offers essential insights for its further development and application in actual search-and-rescue scenarios.

6. Discussion

In this research project, simulation results indicate that the combination of the A* algorithm and the TSP algorithm performs best in multi-target search and rescue tasks, significantly reducing path costs and computation time (Figure 8). In physical tests, the robot was able to reliably execute the improved algorithm and successfully complete tasks in complex environments, validating the feasibility of the improved algorithm. However, in scenarios with fewer target points, the use of the TSP algorithm may increase computational overhead, leading to longer path planning times. This suggests that the algorithm’s advantages are most pronounced in complex multi-target scenarios, while its optimization effects are relatively limited in simpler tasks.

Despite the demonstrated effectiveness of the improved algorithm, there are still some limitations. First, the physical experiments are influenced by environmental factors, such as ground friction and uncertainties in path-smoothing techniques, which may cause some deviations in the robot performances. These deviations caused certain limitations to the physical validation of the improved algorithm. Second, the experimental environment is a relatively controlled maze-like scenario, which has lower complexity and unpredictability compared to real disaster scenarios. Therefore, the algorithm’s adaptability to real-world applications requires further validation.

Additionally, due to time and equipment constraints, the current study primarily focuses on single-robot path optimization. However, the development of multi-robot collaborative search-and-rescue systems is crucial to the advancement of search-and-rescue robot research. Ko and Lau proposed a robot-assisted emergency rescue system that integrates wireless sensor networks, highlighting the advantages of multi-robot cooperation, such as more efficient data collection, faster environmental monitoring, and more precise victim localization [24]. This multi-robot system enables data sharing through the sensor network, facilitating information fusion in dynamic environments and enhancing decision-making capabilities. Moreover, Murphy explored the application of marsupial robots and shape-shifting robots in urban search-and-rescue missions, demonstrating the adaptability and collaborative potential of multi-robot systems in complex terrains [26]. For example, larger robots can carry smaller robots into narrow spaces or transform their shapes to adapt to different rescue environments, significantly increasing the coverage area and efficiency of rescue operations [26]. Therefore, path planning and task allocation in multi-robot systems are key factors in improving overall rescue efficiency. The development in this area will be a potential key focus of the project's next phase.

7. Conclusion

This project successfully developed a search and rescue robotic system based on an improved algorithm and validated the superiority of integrating the A* and TSP algorithms in multi-target path planning. Experimental results demonstrate that the algorithm effectively enhances the robot’s navigation efficiency in complex environments while maintaining low computational costs. The combination of simulation tests and physical experiments further confirms the feasibility of the improved algorithm in real-world applications and provides data support for future optimization of search and rescue robotics.

This project has significant practical value. With the increasing frequency of natural disasters and human-made incidents, efficient search and rescue robots can perform more precise and rapid target search tasks within critical rescue timeframes, thereby reducing the risk of casualties. The improved path planning algorithm not only enhances the search-and-rescue capability of individual robots but also builds a base for future intelligent rescue systems, providing a reliable solution for disaster response.

Future research can further optimize the system in several aspects. First, integrating more advanced SLAM technology could improve the accuracy of environmental mapping, making the robot more adaptable to dynamic and complex rescue scenarios. Second, as mentioned in the previous section, exploring multi-robot collaborative operations could optimize overall rescue efficiency through task allocation and information sharing. Additionally, incorporating increasingly powerful machine learning and AI technologies today could further enhance the intelligence of path planning, enabling robots to develop stronger autonomous learning and adapting capabilities to better handle dynamic changes in unknown environments.