1. Introduction

Truss structures are widely employed in bridge and building engineering due to their advantages of lightweight, high stiffness, and flexible configurations. However, prolonged service durations subject these structures to performance degradation under coupled effects of environmental erosion, external impacts, and fatigue loads, leading to cumulative damage of varying severity. Failure to promptly identify and repair such damage may trigger catastrophic safety incidents, as exemplified by the 2006 collapse of De la Concorde Overpass in Quebec, Canada, where fatigue crack propagation in steel truss web members and inadequate monitoring were identified as primary causes [1]. This underscores the critical engineering significance of structural damage identification research for ensuring operational safety, optimizing maintenance strategies, and extending service lifespan [2].

In the field of structural damage identification, Bayesian methods have achieved notable advancements. Sohn et al. [3] proposed a Bayesian probabilistic framework combined with finite element models to detect the most probable damage locations and severity in structures. Vanik et al. [4] applied Bayesian methodologies to structural health monitoring, identifying damage through simulated data. For complex structural damage identification challenges, Ching and Chen [5] introduced an efficient Markov Chain Monte Carlo (MCMC) algorithm, significantly enhancing computational efficiency. Gao [6] conducted improvement studies on Bayesian model updating methods. Additionally, Mukesh et al. [7] developed finite element model updating techniques for nonlinear systems, offering a novel approach for advancing structural health monitoring technologies based on field-measured data.

Despite groundbreaking progress in the theoretical framework and engineering applications of Bayesian updating mentioned above, existing literature still lacks systematic investigation into the quality of parameter information during Bayesian-based damage identification processes. To address this gap, this study establishes a coupled framework integrating Monte Carlo methods and Bayesian updating, and develops an OpenSees-based finite element model of truss structures for damage identification research. By employing parameter correlation analysis methods, we quantitatively evaluate the sensitivity characteristics of parameter information to target variables and delve into the mechanisms through which information quality influences Bayesian updating processes.

2. Methods

2.1. Introduction of Monte Carlo method

The Monte Carlo method is a numerical computational approach based on stochastic sampling and statistical simulation, whose core principle lies in solving problems through extensive trials [8-9]. It is thus widely applied in fields such as quantifying uncertainty [10], financial sensitivity analysis [11], and engineering risk assessment [12], as well as in structural reliability analysis for calculating failure probabilities in engineering. This study primarily employs rejection sampling, a classical Monte Carlo technique, to generate random samples from the complex distribution of the target structure. The method involves selecting a simple proposal distribution \( q(x) \) and a constant M such that \( M∙q(x) \) envelopes the target distribution \( p(x) \) . Candidate samples are drawn from \( q(x) \) , and their acceptance is determined by the probability \( α=\frac{p({x^{*}})}{M({q^{*}})} \) . This technique is extensively utilized in Bayesian inference.

2.2. Introduction of Bayesian updating method

Bayesian updating is a statistical method based on Bayes' theorem \( P(A|B)=\frac{P(A)P(B|A)}{P(B)} \) . Bayesian updating dynamically refines the probability distribution (posterior distribution) of unknown parameters by integrating prior knowledge with newly acquired data. Its core principle lies in iteratively updating the posterior distribution as additional data becomes available, thereby refining information through data assimilation. Fundamental concepts are detailed in [13]. This study focuses on Bayesian model updating within the context of structural health monitoring (SHM) [14], examining the updating effectiveness for structural damage to explore data information quality issues inherent in Bayesian.

3. Numerical example

3.1. Modelling

A statically indeterminate truss structure model is illustrated in Fig. 1, with the following global geometric parameters:

Total length of the structure: 40 meters, with each member of the lower chord measuring 10 meters in length.

Structural height: 10 meters, where Nodes 7 and 8 are positioned 10 meters vertically above the lower chord, while Nodes 6 and 9 are located at a vertical distance of 5 meters from the lower chord.

All members initially exhibit identical axial stiffness EA.

Structural health monitoring revealed varying degrees of damage in Members 3, 7, and 11: Member 3 (Axial stiffness reduced to 0.9EA), Member 7 (Stiffness degraded to 0.7EA), Member 11 (Stiffness decreased to 0.8EA). It is critical to note that the measured stiffness parameters exhibit random errors, which follow a normal distribution with a mean of 0 and standard deviation of 0.05.

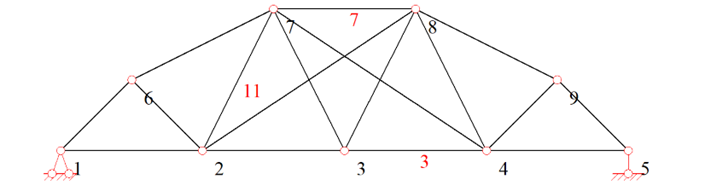
Figure 1: Truss structure

To determine the specific damage outcomes of Members 3, 7, and 11, the structure will be subjected to loading under two predefined schemes:

Loading Scheme 1: Apply vertical downward compressive forces of 100 kN at Nodes 7 and 8, as illustrated in Fig. 2.

Loading Scheme 2: Building upon Scheme 1, introduce an additional vertical upward reaction force of 100 kN at Node 2, as shown in Fig. 3.

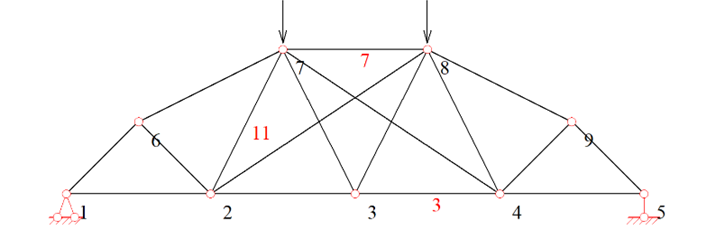
Figure 2: Loading Scheme 1

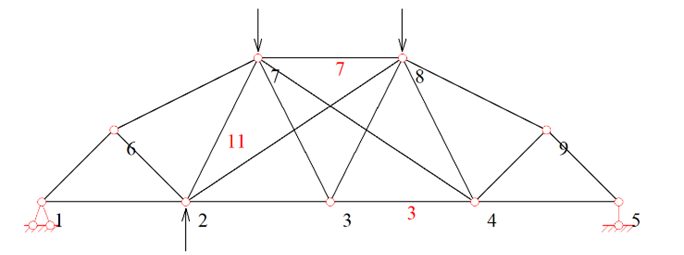
Figure 3: Loading Scheme 2

3.2. Analysis of effect

3.2.1. Comparison of loading test and update results

By integrating Bayesian updating with Monte Carlo methods, a numerical framework was implemented using the OpenSees-based model. Leveraging displacement data from Nodes 2, 3, 4, 7, and 8, 100,000 iterations of rejection sampling were performed on the truss structure under Loading Scheme 1, yielding the structural damage updating results depicted in Fig. 4, Fig. 5, Fig. 6.

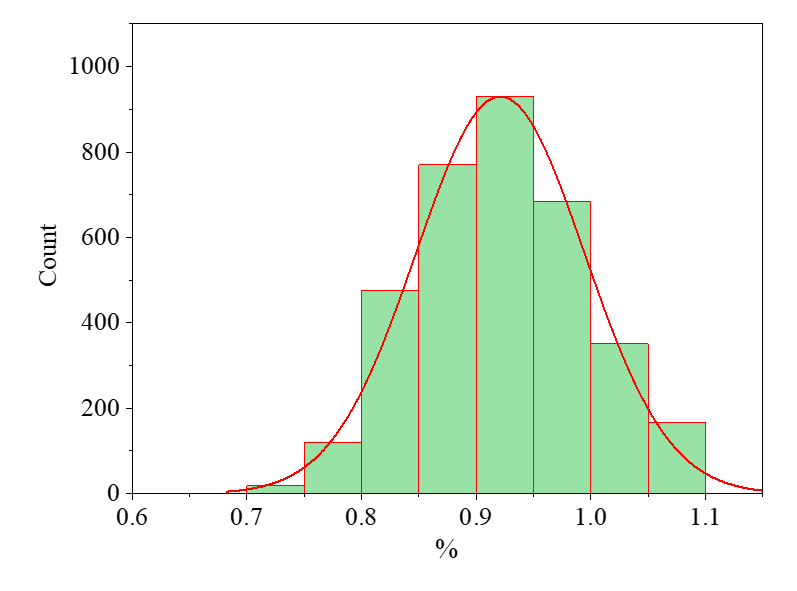
Figure 4: Loading Scheme 1 Member 3 update results

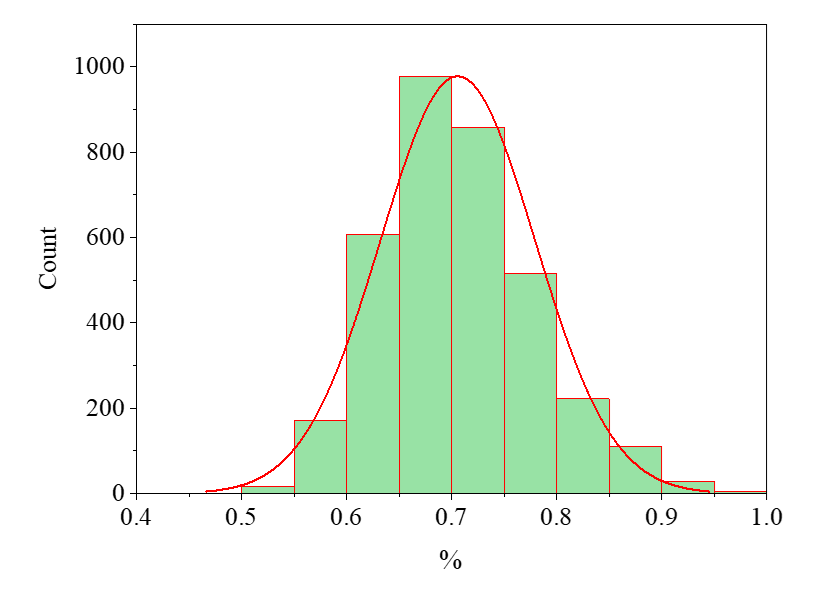
Figure 5: Loading Scheme 1 Member 7 update results

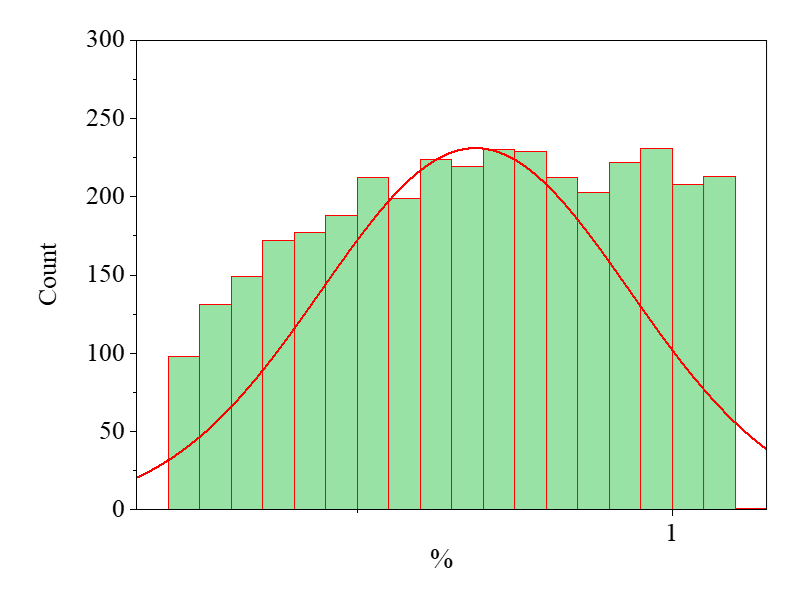
Figure 6: Loading Scheme 1 Member 11 update results

When compared to the preset prior, the structural damage updating effectiveness for Members 3 and 7 demonstrates notable improvement, whereas the updating performance for Member 11 remains suboptimal. To address this limitation, Loading Scheme 2 was proposed to enhance the updating accuracy for Member 11. Employing the same methodology, 100,000 iterations of rejection sampling were conducted on the truss structure under Loading Scheme 2, yielding the structural damage updating results illustrated in Fig. 7, Fig. 8, Fig. 9.

Figure 7: Loading Scheme 2 Member 3 update results

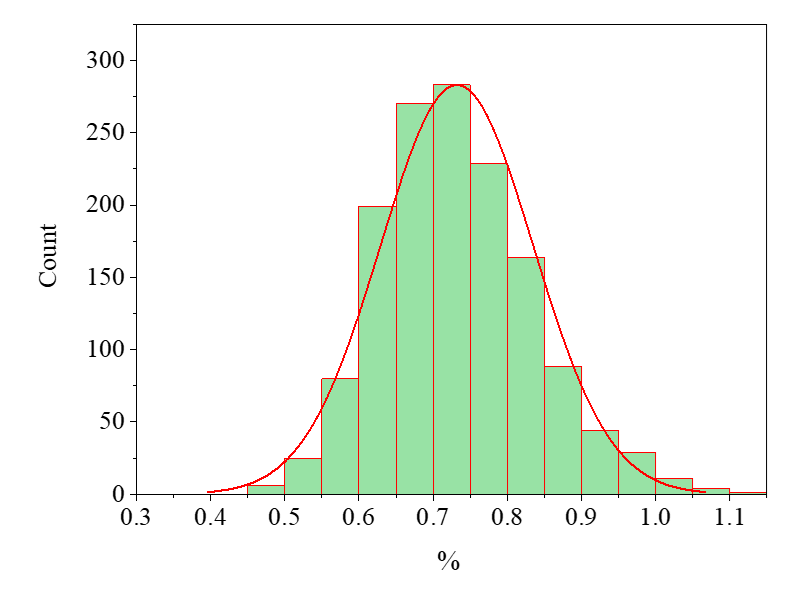
Figure 8: Loading Scheme 2 Member 7 update results

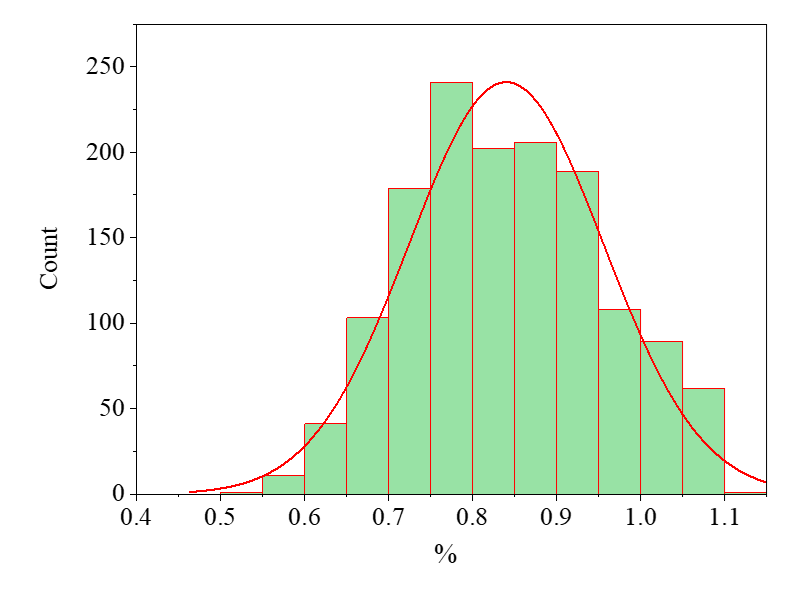
Figure 9: Loading Scheme 2 Member 11 Update result

3.2.2. Correlation analysis based on Bayesian update effect

For Loading Scheme 1, a correlation analysis using the CORREL function was applied to randomly generated displacement samples and the stiffness of members requiring updating, yielding the results summarized in Table 1.

From Table 1, it is evident that the displacement data from the five monitored nodes (2, 3, 4, 7, 8) exhibit weak correlations with the stiffness of Member 11, indicating that these nodes are insensitive to stiffness variations in Member 11 under the first loading scheme. Consequently, the updating results derived from these nodal displacements are highly unreliable.

In contrast, for Loading Scheme 2, the same correlation analysis was performed, with results presented in Table 2. The analysis reveals a significant enhancement in correlations between the stiffness of Member 11 and displacements at Node 2 and Node 7, as visually corroborated by Fig. 10 and Fig. 11. The scatter plots demonstrate a discernible linear relationship, confirming that these nodes exhibit improved sensitivity to stiffness changes in Member 11 under the second loading scheme.

Figure 10: Scatter plot of correlation between Node 2 displacement and Member 11 stiffness

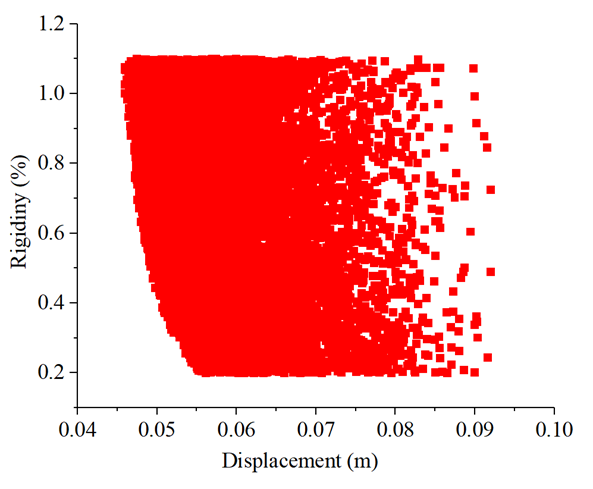
Figure 11: Scatter plot of correlation between Node 7 displacement and Member 11 stiffness

Regarding information quality, under Loading Scheme 2, only the displacements of two highly correlated nodes (Nodes 2 and 7) were utilized for updating Member 11, and the results were compared against those derived from all five monitored nodes. As illustrated in Fig. 12 and Fig. 13, the updating effectiveness for Member 11 based on two-node displacement measurements shows negligible deviation from that achieved using five-node data. This demonstrates that selecting high-correlation, high-quality information while discarding low-correlation, low-quality data can yield comparable or superior updating outcomes while significantly reducing measurement costs.

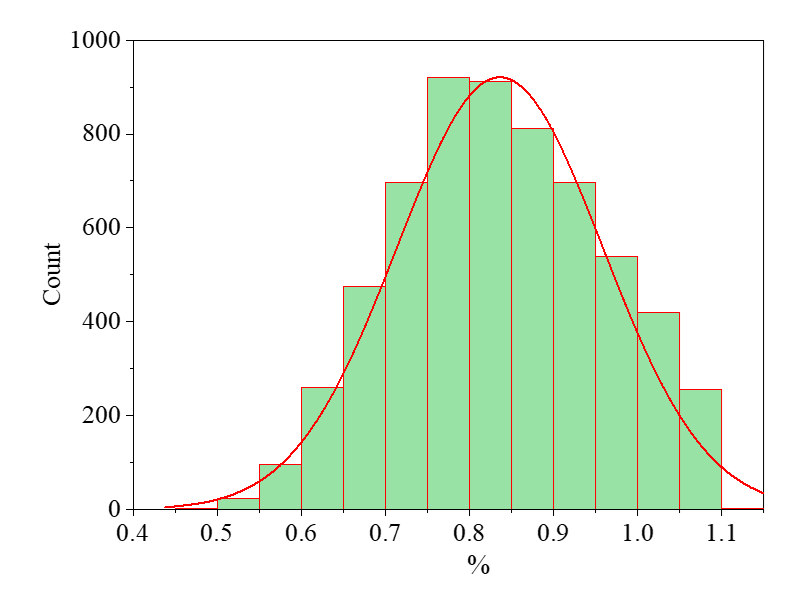
Figure 12: Updated results using only two node displacement information

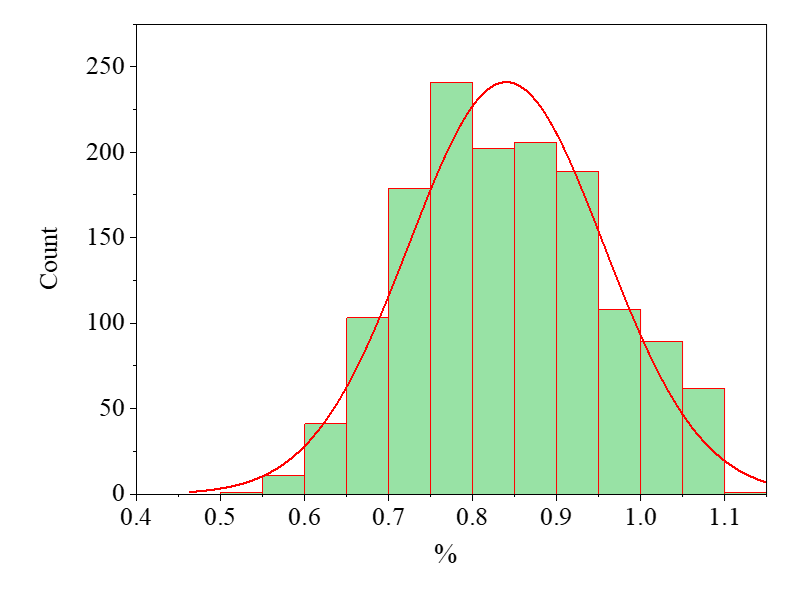
Figure 13: Updated results using five node displacement information

Building upon these findings, Loading Scheme 2 was reapplied using displacement data from all nodes to update the truss structure. A correlation analysis via the CORREL function was conducted between randomly generated displacement samples and the stiffness of members requiring updating, with results summarized in Table 3. The analysis reveals that Members 2 and 6, as well as Members 4 and 9, exhibit nearly identical correlations with the target members requiring updating. This implies that measuring either member from these pairs (e.g., Member 2 or 6) suffices to achieve optimal updating outcomes. Consequently, redundant data with equivalent updating effects can be systematically filtered out without compromising the accuracy of the damage identification process. and 6, as well as Members 4 and 9, exhibit nearly identical correlations with the target members requiring updating. This implies that measuring either member from these pairs (e.g., Member 2 or 6) suffices to achieve optimal updating outcomes. Consequently, redundant data with equivalent updating effects can be systematically filtered out without compromising the accuracy of the damage identification process.

Table 1: Displacement correlation with member stiffness in Loading Scheme 1

Table 2: Displacement correlation with member stiffness in Loading Scheme 2

Table 3: Correlation between all nodal displacements and member stiffness in Loading Scheme 2

4. Conclusion

Given the critical role of structural damage identification in engineering safety assessments, this study establishes a truss structure damage identification model based on a Monte Carlo-Bayesian updating framework, employing Bayesian probabilistic updating methods to elucidate the significant influence of information quality on the damage identification process. The primary contributions are summarized as follows:

1) Inefficiency of Low-Quality Information: Under Loading Scheme 1, Bayesian probabilistic updating analysis reveals the inefficacy of low-quality information (weakly correlated data) in damage updating processes, highlighting its limited contribution to resolving structural uncertainties.

2) Mechanism of Information Quality Impact: By contrasting probabilistic updating outcomes under Loading Scheme 2, the study systematically demonstrates how information quality governs identification accuracy. Findings indicate that prioritizing high-quality (strongly correlated) observational data significantly enhances damage identification efficiency, enabling higher-precision probabilistic updates under constrained resource conditions.

3) Empirical Validation and Future Directions: Empirical results confirm that information quality optimization effectively improves identification performance. However, optimal load augmentation patterns and displacement sensor placement strategies for truss structures remain subjects for further exploration. Subsequent research will focus on algorithmic refinement and extending applications to broader engineering scenarios.