1. Introduction

In recent years, current CFD simulation research on Venturi flowmeters has witnessed significant progress, with numerous scholars making in - depth explorations from different perspectives.

Zhang Yongsheng et al. initiated the use of FLUENT to simulate the transient flow field of Venturi flowmeters and constructed a corresponding mathematical model [1]. Building on this foundation, Liu et al. turned their attention to small - diameter cryogenic Venturi flowmeters. They studied the performance of such flowmeters and explored effective optimization methods [2]. In the context of nuclear power plants, Zhao Erlei et al. addressed the practical problem of measurement fluctuations of Venturi flowmeters in low - flow scenarios and put forward an optimized design [3]. When it comes to the study of multiphase flow, Deng Rong et al. analyzed the water - air two - phase flow in double Venturi tubes using the Eulerian multiphase flow model, enriching the research on the multiphase flow characteristics of Venturi flowmeters [4]. In addition, Yang Jie et al. concentrated on the long - term operation issues of Venturi flowmeters in nuclear power plants. They specifically studied the wear of the main feed water Venturi flowmeters in nuclear power plants [5]. Beyond the traditional research on flowmeters themselves, Zhang Xinwei et al. combined Venturi flowmeters with practical engineering applications. They designed water - fertilizer integration equipment and used CFD to analyze the mixing uniformity in the equipment, expanding the application scope of Venturi flowmeters [6]. Pan, J. et al. analyzed solid-liquid two-phase flow erosion in hydraulic machinery using CFD, focusing on Venturi tubes under varying velocities and sediment conditions, providing erosion prediction insights [7].

Currently, research on the Venturi effect mainly focuses on the measurement of two-phase flow and the Practical Application of Venturi Flowmeters. This paper extends existing research by focusing on single-phase fluid flow in pipeline systems, specifically exploring how pipeline section length, Venturi tube throat diameter, and structural deviations impact flowmeter accuracy. The study emphasizes how roughness and welding flaws affect measurement, contributing to the understanding of Venturi flowmeter behavior.

2. Numerical simulation of venturi tube flow

2.1. Pre-processing on geometric modeling

The Venturi flowmeter is a common differential pressure flowmeter with a variable diameter tube structure, including a throat and two tapered tubes. The structure size is shown in Figure 1 (a).

Size diagram of venturi tube (b) Numerical simulation size diagram

Figure 1: Venturi tube schematic diagram

The inlet pressure measuring point is P₁, and the outlet is P₂, with the pressure difference ∆P. So, measuring ∆P between P₁ and P₂ can determine the flow rate.

Due to the influence of resistance loss,C is introduced to represent the ratio between the actual flow and the theoretical flow. Basing on the Venturi tube in this study, it can be obtained:

\( {q_{m}}=0.03745C\sqrt[]{2ΔPρ} \) (1)

The pressure difference coefficient can be obtained by selecting the fluid density ρ and the average flow velocity v₁ as the basic quantities:

\( {C_{ΔP}}=ΔP/\frac{1}{2}ρv_{1}^{2} \) (2)

When fluid passes through the throat of a Venturi flowmeter, the cross - section shrinks, causing the Venturi effect: increased flow rate and pressure drop. To ensure accurate measurement, the flowmeter design considers sufficient fluid flow distance and wall roughness. An established 3D model, five times the size of the Venturi tube like Figure 1 (b), helps simulate roughness better.

Once the model is set up, the geometric domain is discretized through meshing. For the simple structured Venturi tube, CFD software generates structured tetrahedral meshes. Due to the large and complex flow field in the throat area, boundary-layer meshing is applied to the throat and near-wall surfaces to improve experimental accuracy and reliability. Figure 2 (a) shows the quality of generated tetrahedral and hexahedral meshes, indicating good - quality grids.

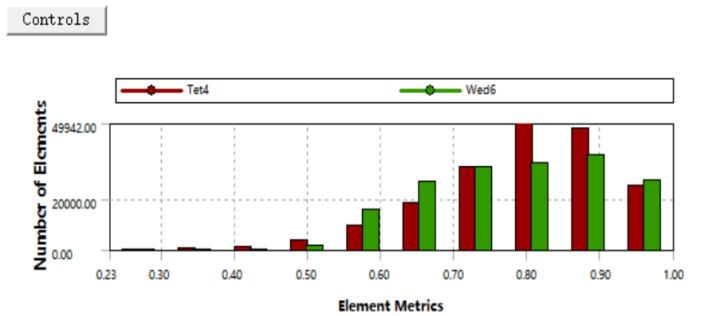
Grid quality diagram (b) Grid independence verification

Figure 2: Grid quality diagram

Before numerical simulation, grid size and quantity independence must be verified to ensure experimental accuracy. This study conducted grid independence analysis based on the Venturi flowmeter's throat center velocity. Figure 2 (b) shows throat center velocity changes across grid numbers, revealing stability after a certain threshold, with errors below 0.13%. Approximately 420,000 grids were selected, with refinement in central and near-wall regions to enhance simulation reliability.

2.2. Venturi tube flow field simulation

Numerical simulations of the Venturi tube flow field under various loads were conducted, calculating the outflow and pressure difference coefficients. Figure 3 analysis indicates that as flow rate increases, the outflow coefficient exhibits a nonlinear growth pattern. The growth rate of the outflow coefficient and the reduction rate of the pressure difference coefficient decelerate and stabilize over time, especially at low flow rates.

The change of outflow coefficient (b) The change of pressure difference coefficient

Figure 3: C and C_ΔP under different working conditions

2.3. Effect of wall roughness

The roughness has a significant effect on the flow field which will increase the flow resistance loss, resulting in an increase in the pressure difference, causing the reading to appear falsely high.

Table 1: Roughness value diagram

The roughness height parameter of the inner surface of the pipe can be Ra or K. In

Table 1: Roughness value diagram, Ra represents the arithmetic mean deviation from the measured (roughness) profile, which can be measured by the electronic average surface roughness instrument. K represents the equivalent uniform roughness in unit length mm. When selecting different Roughness Height parameters, the Roughness Constant is usually set to 0.5 by default.

Figure 4 shows that the pressure difference coefficient and discharge coefficient of the flowmeter change under different roughness and load conditions. The increase of roughness leads to the decrease of pressure an the increase of flow velocity. In particular, the roughness varies significantly in the range of 0 to 0.1 mm.

Figure 5 shows that the roughness of the inner wall of the pipeline increases, the pressure difference measured by the flowmeter increases, and the outflow coefficient decreases. The pressure difference coefficient is the opposite. The roughness has a significant effect on the outflow coefficient in the range of 0 to 0.05 mm. The increase of roughness leads to the increase of flow resistance and pressure difference, and the measurement reading may be inflated. However, the error is only 1.993 %, and the error decreases with the increase of Reynolds number, and the deviation is acceptable.

(a) Roughness height 0mm (b) Roughness height 0.1mm (c) Roughness height 0.3mm

Figure 4: Effect of roughness on velocity distribution

Variation curve of outflow coefficient (b) Pressure difference coefficient curve

Figure 5: The influence curve of roughness on C and C_ΔP

2.4. Influence of pipeline connection on measurement accuracy

Installation of flowmeters and pipe welding may cause deviations that affect measurement. The results show that the different structural parameters of the ratio of the height of the annular baffle to the radius of the pipeline will affect the flow characteristics, pressure difference characteristics and system performance of the Venturi tube, and the mechanism of the structural parameters on the flow characteristics is deeply understood.

Lower than the pipe diameter (b) Higher than the pipe diameter

Figure 6: Structure diagram of flowmeter and pipeline parameter variation

Figure 6 shows the structure of the flowmeter when the pipe diameter is greater than or less than the pipe diameter, and the numerical simulation is carried out.

The unsmooth welding at the pipeline-flowmeter junction increases local flow resistance, disrupting flow field uniformity, leading to higher pressure differences and elevated flowmeter readings. Figure 7 and Figure 8 indicate that a flowmeter diameter smaller than the straight pipe's raises local resistance, particularly at the contraction section's annular baffle. As pipe diameter grows, the flowmeter's throat velocity rises significantly, greatly affecting measurement accuracy.

(a) Lower than the pipe diameter (b) Higher than the pipe diameter

Figure 7: Pressure contour

(c) Lower than the pipe diameter (d) Higher than the pipe diameter

Figure 8: Velocity contour

The data in Figure 9 show that the pressure difference before and after the flowmeter does not change much in the small diameter pipeline. However, in large-diameter pipelines, the pressure difference increases exponentially, mainly due to the increasing influence of local resistance on the flow field. As the height of the pipeline deviation increases, the reading deviation also increases, highlighting the importance of the matching of the pipeline diameter and the flowmeter to measurement accuracy.

(a) Pressure difference diagram (b) C,ΔP diagram

Figure 9: Numerical simulation of flow meter and pipeline structure change

3. Conclusion

Analysis suggests multiple factors lower the outflow coefficient, yet experimental data do not consistently show high readings. Possible reasons include model deviations, insufficient data analysis, and single-factor limitations. The apparent high flowmeter reading may stem from flow rate and wall roughness, but discrepancies between the model and actual results limit the observed degree of false elevation.

To reduce the impact of wall friction and imprecise welding on the readings of a Venturi flow meter, the design should optimize the inner wall material and geometric structure. Selecting smooth materials or applying polishing and coatings to reduce the inner wall roughness and friction, thereby enhancing measurement accuracy. Additionally, optimizing the shape and angle of the converging and diverging sections of the Venturi tube to promote smooth fluid flow, reducing eddies and energy loss. Furthermore, assess the impact of the welding process on measurement accuracy and design specific welding structures and interfaces to ensure precise welding, reducing fluid disturbance and measurement errors. To ensure flowmeter accuracy and reliability, future research should consider more influencing factors and explore comprehensive analysis methods, Like establishing a mathematical compensation model to reduce the interference of different influencing factors on the measurement results, in order to improve the measurement accuracy.