1. Introduction

Seismic signal classification constitutes a critical component of earthquake early warning (EEW) systems, as its accuracy critically determines the timeliness and reliability of warnings, which are paramount to safeguarding lives and mitigating property damage. With the continuous improvement of global seismic monitoring networks, massive amounts of seismic data are collected. However, noise in this data severely interferes with feature extraction, making accurate classification of seismic signal and noise a highly challenging task.

In the field of seismological research, traditional machine learning methods such as Support Vector Machines (SVM) and Random Forests have been extensively investigated and have demonstrated considerable application value and potential in seismic signal classification tasks [1]. developed a SVM classifier based on discriminative features of the data to categorize seismic events occurring in the Tianshan Orogenic Belt of China [2]; utilized the amplitudes of P-waves and S-waves as feature vectors, employing different SVM kernel functions to distinguish between earthquakes and explosions [3]; implemented nonlinear approaches including Random Forests, SVM, and Naive Bayes Classifier (NBC) for seismic event discrimination [4]; trained a Generative Adversarial Network (GAN) to extract primary characteristics of early P-waves, which were subsequently used by Random Forests for waveform classification [5]; applied supervised Random Forests to classify windowed seismic data within continuous data streams [6]; established discriminators using Fisher classifiers, Naive Bayes classifiers, and logistic regression to differentiate between seismic events and seismic waves generated by explosions.

With the advancement of deep learning, methods such as Convolutional Neural Networks (CNN), Long Short-Term Memory networks (LSTM), Transformer, VGG, and AlexNet have been widely applied in seismic signal classification. CNNs were employed using aftershock data from the Wenchuan earthquake to classify seismic events from noise [7]; [8] adopted various approaches including Support Vector Machines (SVM), eXtreme Gradient Boosting (XGBoost), LSTM networks, Residual Neural Networks, and Long Short-Term Memory-Fully Convolutional Networks (LSTM-FCN) to construct binary and ternary classification models for distinguishing tectonic earthquakes, explosions, and mining-induced seismic events; Recurrent Neural Networks (RNN), LSTM networks, and Gated Recurrent Units (GRU) were utilized to extract temporal and frequency information from continuous seismic data, enabling effective detection and classification of seismic events [9]; The CCViT [10] model combines CNNs with Transformer to accurately identify genuine microseismic signals [11]; implemented four distinct CNN architectures, namely AlexNet, VGG16, VGG19, and GoogLeNet for efficient identification of natural earthquakes, explosions, and collapse events; The seismic event classification model presented in [12] integrates waveform data from multiple stations and employs CNNs with Graph Convolutional Networks (GCNs) to enhance classification performance [13]; investigated the classification performance of Multilayer Perceptron (MLP) neural networks for seismic signals in the Agadir region.

Both traditional machine learning methods and deep learning methods have several core limitations. Traditional machine learning methods are highly dependent on feature engineering. Researchers need to rely on profound professional knowledge and rich experience to manually extract and screen suitable features, and this process has a significant impact on the final classification results. Moreover, traditional methods are extremely prone to falling into overfitting, which in turn leads to a decline in classification accuracy. Although deep learning methods have advantages in automatic feature extraction, they also have the problem of insufficient long-range dependence. Seismic signal has complex time series and spatial relationships, while deep learning models often have difficulty effectively capturing and utilizing long-range dependence information. In addition, the Multilayer Perceptron (MLP) has limited capabilities in handling complex nonlinear relationships and has the "black box" problem.

Based on the above issues, this paper proposes a new hybrid architecture, ResNetKAN1D. By introducing a dual attention mechanism into the residual network, including channel attention and spatial attention, it greatly solves the problem of the difficulty in simultaneously capturing the features of seismic signal in both the temporal and spatial dimensions. At the same time, the Kolmogorov-Arnold Network (KAN) is adopted to replace the Multilayer Perceptron (MLP), which avoids the "black box" problem of the MLP and improves the ability of nonlinear modeling. The contributions of this architecture are followings:

(ⅰ) Incorporate dual attention mechanisms to enhance weights for critical regions and channels, improving sensitivity to key features.

(ⅱ) Replace traditional MLP with KAN, creating a hybrid architecture of residual network and KAN. This marks the first application of KAN in seismic signal classification.

(ⅲ) Evaluate the proposed model on the Stanford Earthquake Dataset (STEAD). Results show significant improvements over existing baseline models in accuracy (7.8% increase) and F1 score (0.11% increase).

The remainder of this paper is organized as follows: Section 2 provides an overview of related work. Section 3 describes the proposed methodology. Section 4 presents and discusses the experimental results. Section 5 examines the advantages and limitations of ResNetKAN1D. Section 6 concludes this work.

2. Related work

The attention mechanism is widely applied in the field of deep learning. It enables the model to automatically focus on the key parts of the input data, improving the performance and efficiency of the model. [14] takes the residual neural network as the basic architecture and integrates the channel attention and spatial attention to optimize the network's attention to the key information of seismic waveform signals. In addition, researchers proposed the "Squeeze-and-Excitation" (SE) block [15], which adaptively recalibrates the channel feature responses by explicitly modeling the dependencies between channels; the Convolutional Block Module (CBAM) [16] infers the attention maps along the channel dimension and the spatial dimension and multiplies the attention maps with the input feature maps to achieve adaptive feature optimization. The attention mechanism effectively solves the problem of extracting key features of signals by enhancing the weights of key regions and channels of seismic signals and improves the classification accuracy.

Inspired by the Kolmogorov-Arnold representation theorem, [17] proposed the Kolmogorov-Arnold Network (KAN) as an alternative to the Multilayer Perceptron (MLP). KAN has no linear weights, and each weight parameter is replaced by a B-spline basis function, making KAN superior to MLP in terms of accuracy and interpretability [17]; [18] proposed combining KAN with various pre-trained convolutional neural network models and replacing the traditional MLP with KAN to improve classification performance. KAN enables interpretable nonlinear mapping, captures the complex nonlinear relationships between different features in seismic signal, and models and classifies seismic signal more accurately. It avoids the "black box" problem of MLP and improves the interpretability of the model.

3. Proposed method

The ResNetKAN1D model proposed in this paper is designed for efficient classification of seismic signal. As illustrated in Fig. 1, the model processes raw 3-channel waveform data of size 3×5000 as input data. It first undergoes an initial convolutional layer for preliminary feature extraction, followed by a pooling layer to reduce spatial dimensions. Next, the data passes through four groups of residual blocks (Layer1-Layer4), each composed of multiple residual units. Each unit contains convolutional layers, batch normalization layers, activation functions and dual attention modules. Following the residual blocks, an adaptive average pooling layer adjusts the feature maps to a fixed size. Finally, a KAN classification layer classifies the extracted features.

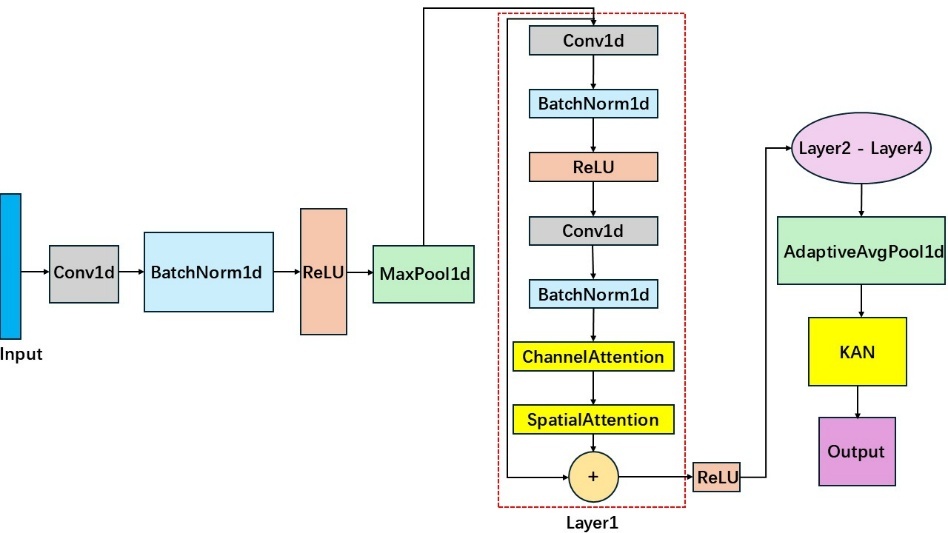
Figure ⅼ: Architecture of ResNetKAN1D

3.1. Feature extraction

The primary function of this model is to extract multi-level and multi-scale features from input data. Taking waveform data shaped [64, 3, 5000] as input data, it first passes through an initial convolutional layer. This transforms the feature map dimensions to [64, 64, 2500]. The output is subsequently processed by a batch normalization layer and activation function. Batch normalization stabilizes data distribution to accelerate model convergence, while the ReLU activation function introduces nonlinearity to enhance model expressiveness. Then the data passes through a pooling layer to reduce spatial dimensions and computational complexity while preserving essential features. After pooling, the feature map dimensions are reduced to [64, 64, 1250]. Next, the data is processed through four groups of residual blocks. Residual blocks are the core of this module, effectively addressing gradient vanishing and explosion issues in deep neural networks, enabling the model to learn more complex and hierarchical features. Each residual block comprises convolutional layers, batch normalization layers, ReLU activation functions, and dual attention modules.

Residual connections facilitate direct information transmission between layers, avoiding information loss in deep networks. Specifically, within each residual block, the input signal is added to the output of the convolutional layer before passing through the activation function. The formula for the residual block is:

\( y=F(x,\lbrace {W_{i}}\rbrace )+x \) (1)

Where \( x \) is input data, \( F(x,\lbrace {W_{i}}\rbrace ) \) is the residual function representing the output after \( x \) through residual layers, and \( \lbrace {W_{i}}\rbrace \) are learnable parameters in the residual block. After processing through multiple residual blocks, the model obtains feature maps at different scales. An adaptive average pooling layer adjusts the feature maps to a fixed size, ensuring consistency of output feature vectors. Following this operation, the feature map shape becomes [64, 512, 1].

3.2. Dual attention module

The dual attention module includes channel attention and spatial attention, with architectures shown in Figs. 2 and 3.

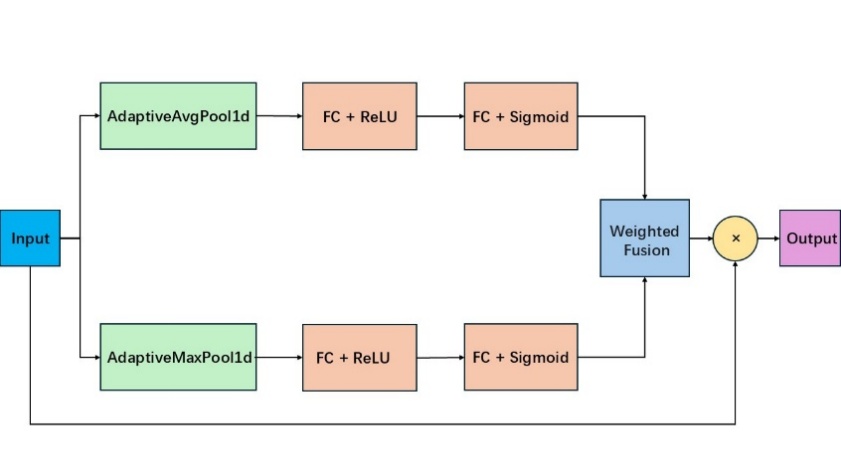
Figure 2: The architecture of channel attention

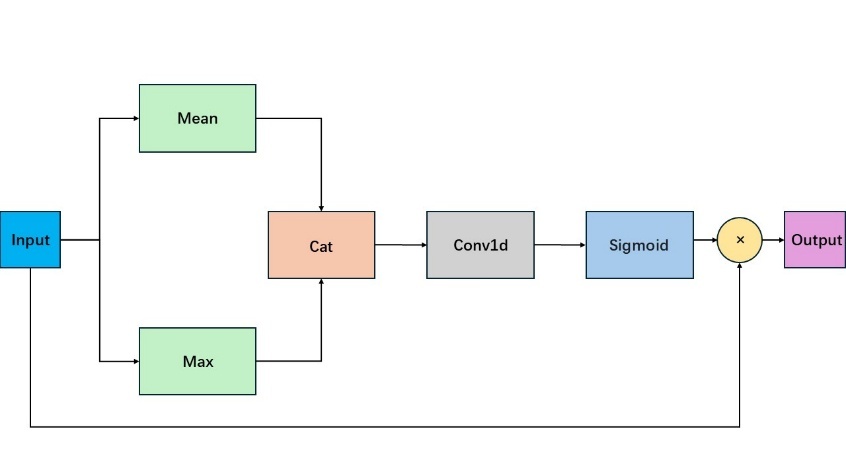
Figure 3: The architecture of spatial attention

3.2.1. Channel Attention (CA)

Channel attention enhances or suppresses features in different channels. It uses global average pooling and global max pooling to obtain average and maximum features for each channel, respectively. These features are input into a sequence of fully connected (FC) layers and activation functions to generate channel attention weights. For input feature \( x \) , after average and max pooling to get \( GAP(x) \) and \( GMP(x) \) , channel attention weights are calculated through FC layers. The input feature is multiplied by these weights to produce weighted channel features, which can be calculated as:

\( CA(x)=x∙σ({W_{2}}∙ReLU({W_{1}}∙[GAP(x);GMP(x)])) \) (2)

where \( {W_{1}} \) and \( {W_{2}} \) are weight matrices of the first and second FC layers, and \( σ \) is the Sigmoid activation function.

3.2.2. Spatial Attention (SA)

Spatial attention focuses on the importance of signal positions within the input data. It performs average and max pooling along the channel dimension to obtain average and max feature maps, denoted as \( Mean(x) \) and \( Max(x) \) , respectively. These maps are concatenated along the channel dimension and input into a convolutional layer to generate spatial attention weights. The input feature is multiplied by these weights to achieve weighted spatial features, as described by the following equation:

\( SA(x)=x∙σ(Conv([Mean(x);Max(x)])) \) (3)

where \( Conv \) represents the convolution operatio.

After processing by the dual attention module, features are optimized in both channel and spatial dimensions, thereby enhancing features critical for classification.

3.3. KAN classification layer

This paper introduces a KAN classification layer utilizing B-spline basis functions to replace MLP. B-spline basis functions are piecewise polynomial functions characterized by local support and smoothness. Compared to traditional neurons, they provide more flexible and interpretable nonlinear mappings, avoiding "black box" issue of MLP.

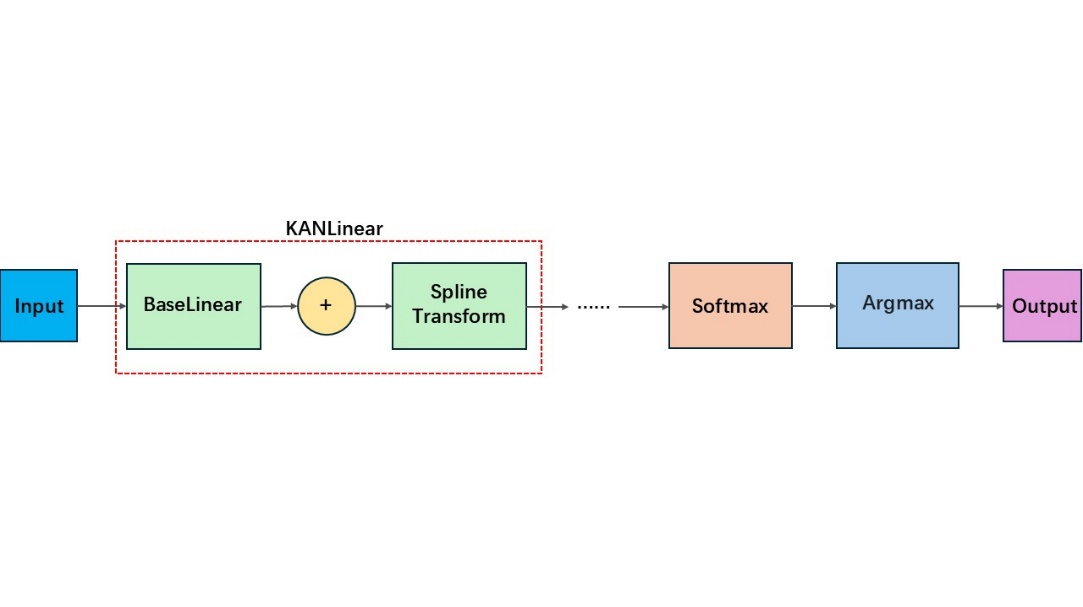
Figure 4: The architecture of KAN

The KAN classification layer consists of multiple KANLinear layers, each contains a base linear layer and a piecewise polynomial layer. The base linear layer performs initial processing of input features through linear transformation, while the piecewise polynomial layer employs B-spline basis functions for further nonlinear transformation to enhance model expressiveness. In a KANLinear layer, the input features are first processed by the base activation function SiLU, which can be calculated as:

\( SiLU(x)=x∙σ(x) \) (4)

Meanwhile, the input features are also used to calculate B-spline basis functions. For each input feature, the model checks whether it lies between two adjacent reference points in the predefined grid. If so, it is marked as "qualified", and these results are converted to the same data type as the input to derive the basis functions, which are then updated using a recursive formula. The calculation formula for the basis function is:

\( {y_{base}}=((x≥Grid[:, :-1])(x \lt Grid[:,1:])).to(x.dtype) \) (5)

where \( Grid \) represents reference point information.

The piecewise polynomial layer performs calculations using the basis functions and piecewise polynomial weights. After reshaping the B-spline basis functions and weights into appropriate forms, a linear transformation is applied to obtain the output \( {y_{spline}} \) . Finally, the output of the KANLinear layer is obtained by summing the outputs of the base linear layer and piecewise polynomial layer, which can be calculated as:

\( Output={y_{base}}+{y_{spline}} \) (6)

The output of each KANLinear layer serves as input to the next layer. The output dimension of the last layer corresponds to the number of classification categories. The Softmax function is applied to the last layer's output to convert it to a probability distribution, and argmax is used for class prediction: category 0 represents noise signal, and category 1 represents seismic signal.

4. Experiments

4.1. Dataset

The Stanford Earthquake Dataset (STEAD)[19] is used for experiments, which is a global seismic dataset designed for seismic signal processing and AI applications, containing 6,800 earthquake events and 5,200 noise events. The dataset is divided into training, validation, and test sets at an 8:1:1 ratio. Data preprocessing includes standardization, P-wave alignment, and random cropping of 50-second signal.

4.2. Comparison with baseline models

Several baseline models are selected as baselines, including ResNet18[20], 1D-CNN[21], AlexNet-1D[22], VGG11-1D[23], and Transformer [24]. These models represent distinct types of deep learning architectures and have been widely applied in seismic signal classification. To ensure fairness and comparability, all baseline models and ResNetKAN1D use the same preprocessing methods and are trained and tested on the STEAD dataset. Table. 1 lists the values of some critical hyper-parameters. Multiple evaluation metrics are used, including Accuracy (Acc), Precision, Recall, and F1-score, which are defined as:

\( Acc=\frac{TP+TN}{TP+FP+FN+TN} \) (7)

\( Precision=\frac{TP}{TP+FP} \) (8)

\( Recall=\frac{TP}{TP+FN} \) (9)

\( F1=2×\frac{Precision×Recall}{Precision+Recall} \) (10)

Table 1: Values of some critical hyper-parameters

The comparison results between ResNetKAN1D and baseline models are shown in Table 2.

Table 2: Benchmark model comparison

As shown in Table. 2, the ResNetKAN1D model demonstrates significant superiority over all baseline models across all evaluation metrics. In terms of accuracy (Acc), it achieves 96.1 ± 0.2%, surpassing the second-best model, ResNet18 (90.3 ± 0.2%), by a notable margin of 5.8%. This indicates that ResNetKAN1D exhibits higher overall classification correctness. Regarding precision, ResNetKAN1D attains a value of 0.95, outperforming ResNet18 (0.88) by 0.07. This improvement suggests that ResNetKAN1D achieves a higher proportion of true positives among predicted positives, thereby reducing misclassification errors. As for recall, ResNetKAN1D achieves 0.96, significantly exceeding ResNet18's 0.87 by 0.09. This demonstrates the enhanced capability of model to identify all positive samples effectively. Furthermore, the F1 score, which represents the harmonic mean of precision and recall, reaches 0.955 for ResNetKAN1D, compared to 0.87 for ResNet18, the highest among the baseline models. This result underscores the superior balance between precision and recall achieved by ResNetKAN1D, highlighting its robust overall performance.

4.3. Ablation study

Ablation experiments evaluate the contribution of each module in ResNetKAN1D. Using ResNet18+MLP as the baseline, we incrementally add channel attention, spatial attention, and KAN modules, or remove them from the full model, and observe performance changes. Results are shown in Table. 3.

Table 3: Result of ablation study

The channel attention mechanism precisely focuses on important feature channels, enabling the model to extract effective information. Taking the baseline model (ResNet18 + MLP) as a reference, its accuracy is 88.7%, with a change of -7.8% compared to the full model, and the F1-score is 0.85. When the channel attention mechanism is introduced, the accuracy increases to 92.3%, and the F1-score rises to 0.91. Removing the channel attention mechanism from the full model, the accuracy drops to 94.2%, with a change of -2.3% compared to the full model, and the F1-score decreases to 0.94.The results indicate that the channel attention mechanism can better capture key features when dealing with seismic signal, which strongly validates the effectiveness of the channel attention module in the model.

The spatial attention mechanism helps the model better capture the spatial relationships in the image and the location information of objects, enabling the model to process the input data more comprehensively. After adding the spatial attention mechanism to the baseline model, the accuracy of the model reaches 91.8%, and the F1-score is 0.90. When the spatial attention mechanism is removed from the full model, the accuracy drops to 95.0%, with a change of -1.5% compared to the full model, and the F1-score decreases to 0.95. This result shows that the introduction of the spatial attention mechanism improves the performance of the model, fully demonstrating the usefulness of this module in the model.

The dual attention mechanism demonstrates a better performance improvement effect compared to a single attention mechanism. When only the dual attention mechanism is used, the accuracy of the model reaches 93.9%, which is higher than that of a single attention mechanism. The two attention mechanisms complement each other, enabling the model to process seismic signal more comprehensively and further enhancing the model's performance. This verifies the effectiveness and advantages of the dual attention mechanism within the model.

By adding the Kolmogorov-Arnold Network (KAN) on the basis of the dual attention mechanism, that is the full model, the accuracy of the model reaches the highest level of 96.5%, and the F1-score is 0.96. This result clearly shows that the combination of KAN and the dual attention mechanism has a significant effect on improving the performance of the model. When KAN is used alone, the accuracy of the model is 90.1%, which is higher than that of the baseline model, indicating that KAN plays a certain role in improving the performance of the model. The experimental results strongly verify the effectiveness of the KAN module in enhancing the performance of the model.

5. Discussion

The ResNetKAN1D hybrid architecture proposed in this study provides an innovative and effective solution for seismic signal classification. By integrating dual attention mechanisms into a deep residual neural network and replacing MLP with KAN layers, the model automatically focuses on key features in seismic signal and enhances nonlinear modeling capabilities. On the STEAD, it achieves an accuracy of 96.1%, precision of 0.95, recall of 0.96, and F1-score of 0.955, outperforming baseline models. The ResNetKAN1D architecture holds considerable promise for earthquake early warning systems, as its high classification accuracy can reduce false alarms and improve reliability. However, the current implementation is limited to single-task classification. Future research should focus on extending the model to multi-task scenarios, such as simultaneous magnitude estimation and hypocenter localization, through architectural refinements or multi-task learning frameworks. Additionally, optimizing the computational efficiency of the KAN module will be critical for practical deployment in real-time systems.

6. Conclusion

This paper introduces a novel ResNetKAN1D hybrid architecture for seismic signal classification, integrating dual attention mechanisms into residual networks and incorporating KAN layers. This is the first application of KAN in the domain of seismic signal classification. To address persistent challenges such as noise interference and feature extraction difficulties, the model employs residual blocks enhanced with dual attention mechanisms to improve key feature selection and leverages KAN layers to enhance nonlinear modeling capabilities. Experimental results on the STEAD demonstrate the model's superior performance, significantly outperforming baseline models in key metrics such as accuracy and F1-score. Ablation studies further validate the contributions of each module, confirming their effectiveness in improving overall model performance. The ResNetKAN1D exhibits considerable potential for applications in earthquake early warning systems and geological research.