1. Introduction

Massive multiple-input multiple-output (MIMO) has been one of the essential methods for wireless communication application [1]. As a typical application of multi-antenna technology, it can make full use of space resources and achieve the effect of improving communication quality, therefore it is becoming more and more critical in the application of LTE and 5G systems [2].Compared with the conventional small-scale MIMO system, hundreds of antennas will be installed at the base station (BS) to serve a group of guests at the meantime in massive MIMO systems [3].It can greatly realize higher multiplexing and energy efficiency [4].

However, due to the increasing number of antennas, the signal detection in the uplink will obtain higher complexity, which can be a vital challenge for massive MIMO. Hence, there are two methods of signal detection that exist today, which can be nonlinear method and linear method respectively. The nonlinear maximum likelihood detection (MLD), as the optimal detection method, usually be prohibited in massive MIMO uplink since it has to traverse all possibilities [5]. Hence, some nonlinear detection algorithms such as sphere decoder (SD), tabu search (TS) and their variants have been proposed to solve the problems [6]. However, it still has an irreducible complexity due to the high dimension of the MIMO systems or the modulation order is high [7]. Another category is linear methods such as minimum mean square error (MMSE) and zero-forcing (ZF) [8]. Even if they can achieve well performance, it can lead to a significant increase in prohibitively computational complexity due to matrix inversion [7]. Therefore, low-complexity approximate matrix inversion becomes a breakthrough to solve this challenge. The Neumann series expansion (NSE) detection algorithm [5] based on the series expansion is a typical category. Meanwhile, the iterative algorithms including the symmetric successive over-relaxation (SSOR) algorithm [9], the Newton based iteration algorithm [10] and the Gauss Seidel (GS) based iterative algorithm [11] are also proposed. Recently, as computers develop rapidly, machine learning and neural networks can also make corresponding contributions in the massive MIMO systems [12].

This letter hopes to find the potential relationship between the various algorithms proposed in the large-scale MIMO system and their respective advantages and disadvantages. To implement near-optimal performance, the Neumann series expansion (NSE) detection algorithm which can approximate the matrix inverse by using the first few terms of the series expansion has been proposed [5]. However, with the scaling up large-scale MIMO systems, the performance of the algorithm to decrease the complexity is not significant. Meanwhile, some iterative algorithms such as the Gauss Seidel (GS) iterative algorithm and the symmetric successive over-relaxation (SSOR) algorithm [11] can replace the matrix inversion by iterative method, thereby improving the convergence speed and reducing the complexity. In order to compromise between complexity and performance, machine learning and neural networks are also applied to communication network devices [12]. The algorithm uses a neural network architecture to adapt existing algorithms and reduce their computational complexity [13], but the performance of bit error rate (BER) does not degrade. Additionally, the letter seeks to identify a better proposal to enhance the algorithm's functionality and reduce its complexity.

The remainder of the essay is structured as follows. Section II offers a brief overview of massive MIMO systems model. Section III describes Neumann series expansion detection algorithm and related performance analysis. Section IV presents a review of previously proposed iterative approaches. Section V shows a leading-edge signal detection algorithm based on neural networks. Finally, conclusions are made in Section VI.

2. System model

In the letter, an uplink large-scale MIMO system is taken into consideration, where the base station (BS) equipped with \( N \) receiving antennas serves \( M \) single-antenna customers simultaneously (usually \( N \gt M \) , e.g. \( N=256, M=32 \) ). Firstly, the parallel transmitted streams for each customer are encoded by a channel encoder, and then the values obtained from the energy-normalized modulation constellation \( Ο \) are mapped to symbols. Then, the received signal vector, which is denoted by \( y = {[{y_{1}}, {y_{2}}, · · · , {y_{N}}]^{T}} \) , at the BS can be described as

\( y=Hx+n \) (1)

where \( H \) is an \( N×M \) complex-valued uplink channel matrix, \( x={[{x_{1}}, {x_{2}}, · · · , {x_{N}}]^{T}} \) denotes the transmitted signal vector which transmitted by the wireless channel, and \( n={[{n_{1}}, {n_{2}}, · · · , {n_{N}}]^{T}} \) denotes a \( N×1 \) additive white Gaussian noise (AWGN) vector which meets the condition \( n ∼ CN(0, {σ^{2}}{I_{N}}) \) .

Here are two prominent MIMO detection method which can realize the near-optimal performance. For ZF algorithm, the estimated symbol vector \( \hat{x} \) by utilizing MMSE detector can be presented as [2]:

\( \hat{x}={({H^{H}}H)^{-1}}{H^{H}}y={W^{-1}}\hat{y} \) (2)

where \( W={H^{H}}H \) is the \( N×N \) Hermitian positive definite matrix and \( \hat{y}={H^{H}}y \) . For MMSE algorithm, the transmitted signal vector \( \hat{x} \) can also be given by

\( \hat{x}={({H^{H}}H+{N_{0}}{I_{K}})^{-1}}{H^{H}}y={Y^{-1}}{y^{MF}} \) (3)

where \( G={H^{H}}H \) denotes Gram matrix. \( Y=G+{N_{0}}{I_{K}} \) denotes the symmetric positive definite matrix. \( {y^{MF}}={H^{H}}y \) is the output of the matched-filter.

3. Neumann series expansion

For the large-scale MIMO system, Neumann series expansion (NSE) is an iterative method that uses the sum of infinite elements to represent complex matrix inversion through polynomial series expansion. Supposing matrix \( A \) is approximate to a nonsingular matrix \( X \) , Neumann series expansion is able to represented as:

\( {A^{-1}}=\sum _{n=0}^{∞}{(I-{X^{-1}}A)^{n}}{X^{-1}}, \) (4)

where the condition \( \underset{n→∞}{lim}{{(I-{X^{-1}}A)^{n}}=0} \) is satisfied. Further analysis, matrix \( A \) is able to be decomposed as \( A=D+E \) , where \( D \) and \( E \) denote the main diagonal of \( A \) and the off diagonal part of \( A \) , respectively. Because of the diagonal advantage, let \( X=D \) , then Neumann series expansion will be obtained:

\( \hat{A}_{k}^{-1}=\sum _{n=0}^{k-1}{(-{D^{-1}}E)^{n}}{D^{-1}} \) (5)

To this end, the computational complexity of \( k \) -term Neumann series is \( O({K^{2}}) \) when \( k≤3 \) . However, if \( k \) is greater than \( 3 \) , the performance of the MIMO systems will suffer severe damage due to the complexity is \( O({K^{3}}) \) at least. Meanwhile, some simulation results which present the BER performance comparison between near-optimal ZF signal detector and Neumann-based signal detector for the \( N×M=256×32 \) massive MIMO system can be obtained in [9]. As the number of iterations increases, the BER performance of Neumann-based signal detector improves and getting closer to the performance of ZF signal detector. Moreover, when the number of iterations \( k= 2 \) , the Neumann-based signal detector obtains the BER performance of \( {10^{-2}} \) requiring the magnitude of signal-to-noise ratio (SNR) is about \( 20 \) dB. However, the detector only requires around \( 7 \) dB when the value of \( k \) is 3 or 4. This also means that it will leads to irreducible complexity when better performance is needed.

4. Iterative method

4.1. Signal detection with gauss-seidel method

Considering that it is too complicated to directly calculate \( {W^{-1}} \) , the GS method is be employed to figure out the complex linear equation system in an iterative way. Since \( W \) is the Hermitian positive definite matrix with probability one, matrix \( W \) can be decomposed as

\( W=D+L+{L^{H}} \) (6)

where \( D \) , \( L \) , and \( {L^{H}} \) represent the diagonal component, the lower triangular component, and the upper triangular component of W, respectively. Hence, the transmitted signal vector \( \hat{x} \) can be shown as below:

\( {x^{(k)}}={(D+L)^{-1}}({y^{MF}}-{L^{H}}{x^{(k-1)}}), k=1, 2, …, \) (7)

where \( k \) denotes the number of the iterations. If the initial conditions associated with \( {x^{(0)}} \) are not given, \( {x^{(0)}} \) is generally substituted into the calculation as a zero vector. However, it is noteworthy that using the zero vector as the initial solution for calculation will have a greater impact on the accuracy of the final result, because the initial solution affects the speed of convergence. Therefore, the exact value of the initial solution \( {x^{(0)}} \) can be got by using NSE in [11] as follow:

\( {x^{(0)}}=\widetilde{W}_{2}^{-1}{y^{MF}} \) (8)

By using GS algorithm, the complexity of the proposed detector is reduced from \( O({K^{3}}) \) to \( O({(k+3)K^{2}}) \) .

Meanwhile, on the basis of the simulation results of [11], we can observe that compared with the NSE-based signal detector, the BER performance of the GS-based signal detector can be close to the Cholesky decomposition method with fewer iterations. For example, the performance of the GS-based signal detector with \( k=1 \) can almost realize the semblable performance of the NSE-based signal detector with \( k=4 \) when the SNR is about \( 14 \) dB. This can prove that the function of the GS-based algorithm is stronger than NSE-based algorithm.

4.2. Signal detection with SSOR method

From Section IV-A, the matrix \( W \) is decomposed into \( D \) , \( L \) , and \( {L^{H}} \) three different parts. Similarly, the SSOR method also avoids matrix inversion in an iterative manner. First, we calculate the first half iteration by the successive overrelaxation (SOR) iteration [3] as below:

\( (D+ωL){\hat{x}^{(k+\frac{1}{2})}}=(1-ω)D{x^{(k)}}-ω{L^{H}}{\hat{x}^{(k)}}+ω\hat{y} \) (9)

Then, we calculate the second half iteration by the same iteration with inverse order as below:

\( (D+ωL){\hat{x}^{(k+1)}}=(1-ω)D{x^{(k+\frac{1}{2})}}-ωL{\hat{x}^{(k+\frac{1}{2})}}+ω\hat{y} \) (10)

where the initial solution \( {x^{(0)}} \) is generally defaulted to a zero vector. Compared with the GS method, the addition of this parameter \( ω \) can improve the accuracy of the operation and also greatly affect the convergence state. The determination or selection of 𝜔 will directly affect the performance or complexity of the SSOR-based detector. Moreover, through a series of equivalent substitutions and logical analysis, a new relaxation parameter \( \bar{ω} \) with negligible computational complexity can be acquired in [9]:

\( \bar{ω}=\frac{2}{1+\sqrt[]{2(1-a)}} \) (11)

where \( a \) is shown as below:

\( a={(1+\sqrt[]{\frac{M}{N}})^{2}}-1 \) . (12)

It can be found that the relaxation parameter \( \bar{ω} \) is a deterministic parameter which is only connected with the number of receiving antennas \( N \) and single antenna users \( M \) for massive MIMO systems.

Furthermore, the total complexity of the proposed signal detector is \( O({2K^{2}}+2K) \) which is far less than ZF signal detector by about one order of magnitude [2]. According to the simulation results of [9], when the number of users is \( 30 \) , it shows that the number of complex multiplications the SSOR-based signal detector needs will not exceed \( 1×{10^{4}} \) , while the ZF signal detector demand is much greater than \( 4×{10^{4}} \) .

4.3. Signal detection with newton method

The Newton iteration method is obtained by considering only the first-order Taylor series, which can avoid large-scale matrix inversion and improve the accuracy through iteration [14]. It can assume that \( X_{0}^{-1} \) is the original estimation of \( {A^{-1}} \) , then the kth Newton iteration estimation is shown by

\( X_{k}^{-1}=X_{k-1}^{-1}(2I-AX_{k-1}^{-1}) \) (13)

When the convergence condition is

m \( ‖I-AX_{0}^{-1}‖ \lt 1 \) (14)

The accuracy and complexity of the Newton iteration method are decided by \( k \) [14]. When \( k=1, \) the complexity of the proposed Newton-based signal detector is \( O(2{K^{2}} + K) \) . As the number of iterations increases \( (k \gt 1) \) , so does the complexity. [10] points out that the estimated result after \( k \) iterations of the Newton iterative method is the same as the result of order \( 2k-1 \) ( \( 2k \) terms) in the Neumann series expansion.

Meanwhile, the relevant simulation data which can be received from in [10] shows that the proposed signal detector when \( k=2 \) achieves the same performance as the Neumann-based signal detector when \( k=3 \) . Moreover, when \( k=1, 2, 3 \) , the BER performance of proposed signal detector are about \( {10^{-1}} \) , \( {10^{-2}} \) and \( {10^{-4}} \) , respectively with the same SNR whose numerical value is around \( 18 \) dB. It can be also known that after three iterations, the performance of the proposed signal detector is able to almost reach the near-optimal performance of the MMSE algorithm.

5. Signal detection based on neural networks

As the massive MIMO systems develop further, machine learning (ML) and neural networks (NNs) are gradually being advocated to improve the performance of future communication systems. Therefore, a novel combination of the data-driven deep unfolded detector and the probability data association (PDA) algorithm for signal detection for massive MIMO systems is recently proposed in [12]. The method adjusts the architecture of the neural networks according to the detection algorithm currently in use, so that the iteration of the algorithm is carried out on the neural network layer.

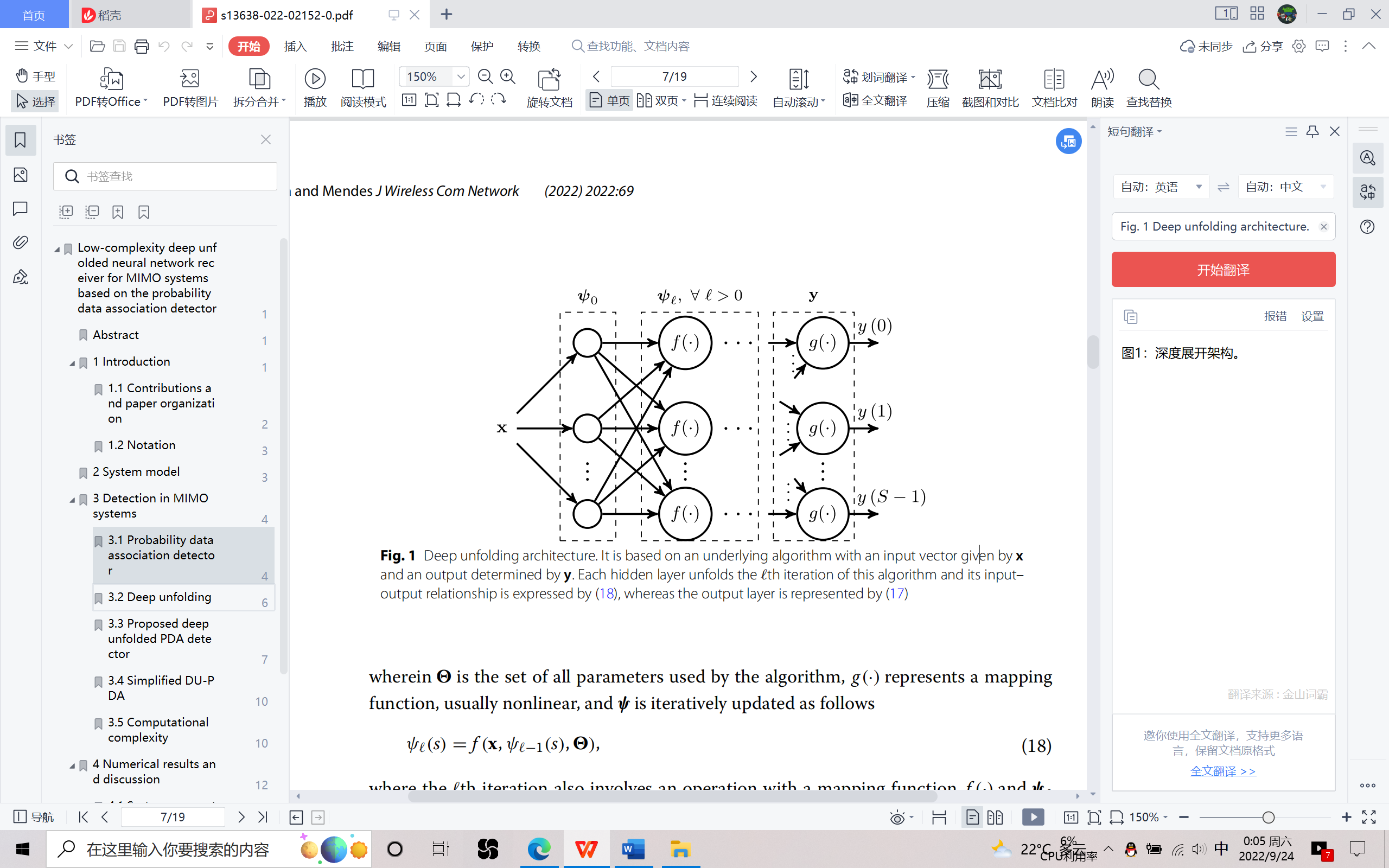
Figure 1. Deep unfolding architecture [12].

Figure 1 shows that it is derived from an underlying algorithm with an input vector and an output vector which are determined by \( x \) and \( y \) , respectively. The \( l \) th iteration of the algorithm can be represented by the expansion of each hidden layer in the structure. \( {ψ_{0}} \) denotes the initial value. Meanwhile, the mapping function \( f(·) \) and \( g(·) \) that are usually nonlinear are supposed to be contained in the algorithm. Therefore, \( {ψ_{l}} \) can denotes the input-output relationship of the \( l \) th neural network layer in the background of deep unfolded. Taking advantage of this special property, the deep unfolded PDA (DU-PDA) algorithm is proposed. Furthermore, to further simplify the algorithm and enhance performance, instead of using optimal Gaussian denoisers, employing the categorical cross-entropy loss function and predigesting the calculation form by using mathematical techniques can carry this point. Ultimately, the general complexity of the proposed simplified DU-PDA detector is reduced to an order of magnitude which is lower than that of the linear ZF detector.

According to the simulation data of [12], in the \( 4×16 \) MIMO system with \( R=1/2 \) and 16-QAM modulation, it can know that the proposed DU-PDA signal detector outperforms the ZF signal detector in the BER performance at \( SNR \lt 8 \) (dB). For example, when \( SNR=4 \) (dB), simplified DU-PDA signal detector and DU-PDA signal detector achieve similar performance at the value of \( BER≈6×{10^{-3}} \) . Nevertheless, the BER performance of ZF signal detector reaches \( {10^{-2}}. \) Meanwhile, during SNR is very small, the proposed signal detector is able to realize the near-optimal performance like ML signal detector or PDA signal detector. Under the condition that other factors remain unchanged, with the increase of SNR, although there is a loss in the performance of the DU-PDA signal detector, it is not harmful to the overall performance in an acceptable range. Therefore, compared with other detectors in terms of performance and complexity, it indicates that the neural network structure shows enormous potential in detecting signals. It is also proved from the above studies that how neural networks are applied in communication systems will become a promising topic for future research [13].

6. Conclusion

In this paper, the relationship between several typical iterative algorithms in the traditional methods of massive MIMO signal detection is introduced. Meanwhile, to realize a more efficient system, a neural network-based signal detection algorithm which is a hotspot in recent years is also proposed. Moreover, a more intuitive understanding of the complexity of these algorithms and the impact on the performance of the detectors can be acquired by analysing the simulation data. Future research will be directed towards various applications of neural networks and machine learning in communication systems.