1. Introduction

With the rapid advancement of the global economy and technological innovation, the automotive industry has witnessed remarkable growth [1-2]. In 2023, global vehicle sales reached approximately 86 million units, underscoring the sector's substantial scale and societal integration [3]. While automobiles have significantly enhanced daily mobility, traditional internal combustion engine (ICE) vehicles [4-5] face increasingly evident limitations, particularly in energy scarcity and environmental pollution. As a result, the development of zero-emission electric vehicles (EVs) [6] driven by renewable energy has become a dominant trend in the automotive industry, reflecting a critical shift toward sustainability and technological innovation.

Recent advancements in battery and motor technologies have significantly enhanced the performance of EVs. However, the rising popularity of high-power EVs has also led to a surge in traffic accidents caused by improper driver operation or deficiencies in vehicle control systems. Effectively managing these "beasts" has thus become a critical concern. Four-wheel-independently driven distributed drive systems can dynamically and optimally distribute the total demanded torque to each actuator, improving vehicle yaw and sideslip control, thereby enhancing handling stability and safety [7].

In this study, a MATLAB simulation model was developed based on research into four-motor distributed drive systems. The control performance of three strategies—no control, average torque distribution, and optimal torque distribution—was compared. The results demonstrate that optimal torque distribution significantly enhances vehicle stability under most operating conditions [8].

2. Dynamic simulation

2.1. Vehicle motion equation

2.1.1. Optimal control allocation

Objective: Distribute the four-wheel torques  $$ T_{fl}$$ ,  $$ T_{fr}$$ ,  $$ T_{rl}$$ ,  $$ T_{rr}$$ ​ to minimize the tire load ratio while satisfying the total driving force and yaw moment requirements.

Optimization Objective Function: Minimize the sum of squared tire load ratios, i.e., minimize energy loss:

$$ \min \left(\frac{{T_{fl}}^2}{{F_{zfl}}^2}+\frac{{T_{fr}}^2}{{F_{zfr}}^2}+\frac{{T_{rl}}^2}{{F_{zrl}}^2}+\frac{{T_{rr}}^2}{{F_{zrr}}^2}\right)$$(1)

 $$ F_{zi}$$  is the vertical load on each wheel.  $$ \frac{{T_i}^2}{{F_{zi}}^2}$$  is the squared tire load ratio, reflecting energy dissipation and friction utilization. A higher vertical load increases the tire’s friction potential.

Constraints:

1. Total driving force equilibrium: The sum of the torques from all four wheels equals the total driving force:

$$ T_{fl}+T_{fr}+T_{rl}+T_{rr}=T_{vx}$$(2)

2. Yaw moment equilibrium: The torque difference between the left and right wheels balances the desired yaw moment:

$$ \frac{B_r}{2r}{(T}_{fl}+T_{fr}-T_{rl}-T_{rr})=M_{yaw}$$(3)

  $$ B_r$$  is the track width,  $$ r$$  is the tire rolling radius, and  $$ M_{yaw}$$ ​ is the yaw moment.

The Lagrangian function is constructed using Lagrange multipliers:

$$ \mathcal{L}=\sum _i\frac{{T_i}^2}{\sum {F_{zi}}^2}+{\lambda }_1\left(\sum T_i-T_{vx}\right)+{\lambda }_2\left[\frac{B_r}{2r}{(T}_{fl}+T_{fr}-T_{rl}-T_{rr})\right]$$(4)

 $$ {\lambda }_1$$ ​ and  $$ {\lambda }_2$$ ​ are Lagrange multipliers.

Taking partial derivatives with respect to each torque and setting them to zero yields:

$$ \frac{\partial \mathcal{L}}{\partial T_{fl}}=\frac{2T_{fl}}{{F_{zfl}}^2}-{\lambda }_1-{\lambda }_2\frac{B_r}{2r}=0$$(5)

$$ \frac{\partial \mathcal{L}}{\partial T_{fr}}=\frac{2T_{fr}}{{F_{zfr}}^2}-{\lambda }_1+{\lambda }_2\frac{B_r}{2r}=0$$(6)

$$ \frac{\partial \mathcal{L}}{\partial T_{rl}}=\frac{2T_{rl}}{{F_{zrl}}^2}-{\lambda }_1-{\lambda }_2\frac{B_r}{2r}=0$$(7)

$$ \frac{\partial \mathcal{L}}{\partial T_{rr}}=\frac{2T_{rr}}{{F_{zrr}}^2}-{\lambda }_1+{\lambda }_2\frac{B_r}{2r}=0$$(8)

The equations reveal symmetry between  $$ T_{fl}$$  and  $$ T_{rl}$$ , and between  $$ T_{fr}$$  and  $$ T_{rr}$$ . The front-rear torque ratios are derived as:

$$ T_{rl}=\frac{{F_{zrl}}^2}{{F_{zfl}}^2}{T}_{fl}$$(9)

$$ T_{rr}=\frac{{F_{zrr}}^2}{{F_{zfr}}^2}{T}_{fr}$$(10)

Substituting these into the constraints:

Total driving force constraint:

$$ T_{fl}\left(1+\frac{{F_{zrl}}^2}{{F_{zfl}}^2}\right)+T_{fr}\left(1+\frac{{F_{zrr}}^2}{{F_{zfr}}^2}\right)=T_{vx}$$(11)

Yaw moment constraint:

$$ T_{fl}\left(1-\frac{{F_{zrl}}^2}{{F_{zfl}}^2}\right)-T_{fr}\left(1-\frac{{F_{zrr}}^2}{{F_{zfr}}^2}\right)=\frac{2r{M}_{yaw}}{B_r}$$(12)

Solving these equations gives:

$$ T_{fl}=\frac{{F_{zfl}}^2}{{F_{zfl}}^2+{F_{zrl}}^2}(\frac{T_{vx}}{2}-\frac{M_{yaw}r}{B_r})$$(13)

$$ T_{fr}=\frac{{F_{zfr}}^2}{{F_{zfr}}^2+{F_{zrr}}^2}(\frac{T_{vx}}{2}+\frac{M_{yaw}r}{B_r})$$(14)

Rear wheel torques are then:

$$ T_{rl}=\frac{{F_{zrl}}^2}{{F_{zfl}}^2+{F_{zrl}}^2}(\frac{T_{vx}}{2}-\frac{M_{yaw}r}{B_r})$$(15)

$$ T_{rr}=\frac{{F_{zrr}}^2}{{F_{zfr}}^2+{F_{zrr}}^2}(\frac{T_{vx}}{2}+\frac{M_{yaw}r}{B_r})$$(16)

Coefficient Simplification:

$$ a_1=r^2({F_{zfl}}^2+{F_{zrl}}^2)$$(17)

$$ b_1=\frac{{F_{zrl}}^2{T}_{vx}{r}^2}{2}-\frac{{F_{zrl}}^2{M}_{yaw}{r}^3}{B_r}$$(18)

 $$ a_1$$  acts as a normalization coefficient, integrating the complex constraints into a single denominator, while  $$ b_1$$  combines the effects of the total driving force and yaw moment on the rear-left wheel into a single numerator term, thereby simplifying the expression for  $$ T_{rl}$$ . Then:

$$ T_{rl}=\frac{b_1}{a_1}=\frac{{F_{zrl}}^2}{{F_{zfl}}^2+{F_{zrl}}^2}(\frac{T_{vx}}{2}-\frac{M_{yaw}r}{B_r})$$(19)

 $$ \frac{T_{vx}}{2}$$ ​​ represents equal distribution of total driving force,  $$ \frac{M_{yaw}r}{B_r}$$  adjusts the torque difference for yaw control, and  $$ \frac{{F_{zrl}}^2}{{F_{zfl}}^2+{F_{zrl}}^2}$$ ​​ weights the torque allocation based on vertical loads.

Similarly, we obtain:

$$ a_2=r^2({F_{zfr}}^2+{F_{zrr}}^2)$$(20)

$$ b_2=\frac{{F_{zrr}}^2{T}_{vx}{r}^2}{2}+\frac{{F_{zrr}}^2{M}_{yaw}{r}^3}{B_r}$$(21)

Then:

$$ T_{rr}=\frac{b_2}{a_2}=\frac{{F_{zrr}}^2}{{F_{zfr}}^2+{F_{zrr}}^2}(\frac{T_{vx}}{2}+\frac{M_{yaw}r}{B_r})$$(22)

2.1.2. Average control allocation

Objective: Distribute the total driving force equally among four wheels, while adjusting the left-right torque difference via  $$ M_{yaw}$$ ​ for stability:

$$ T_{fl}+T_{fr}+T_{rl}+T_{rr}=T_{vx}$$(23)

$$ \frac{B_r}{2r}{(T}_{fl}+T_{fr}-T_{rl}-T_{rr})=M_{yaw}$$(24)

The torque difference  $$ ∆T=\frac{M_{yaw}r}{B_r}$$ 

The aforementioned equally distributed torque allocation scenario is more suitable for simple, low-dynamic conditions. In this method, an increase in torque demand on one side results in a corresponding decrease on the opposite side. However, this approach has inherent limitations, as it neglects vertical load variations, potentially leading to wheel slippage or inefficient torque distribution. In contrast, the optimal allocation strategy accounts for vertical loads, enabling enhanced dynamic performance and energy efficiency.

2.1.3. Linear two-degree-of-freedom vehicle model

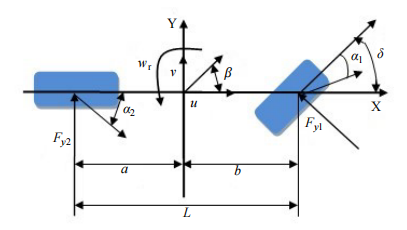
Differential Equations:

$$ \{\begin{array}{c}\dot{\beta }=\frac{k_1+k_2}{m{v}_x}\beta +\left(\frac{a{k}_1-b{k}_2}{v_x}-1\right)w_r-\frac{k_1}{m{v}_x}\delta \\ {\dot{w}}_r=\frac{a{k}_1-b{k}_2}{l_z}\beta +\frac{a^2{k}_1+b^2{k}_2}{l_z}{w}_r-\frac{a{k}_1}{l_z}\delta \end{array}$$(25)

Vertical Loads:

$$ F_{zfl}=mg+\frac{mg{L}_r}{2L}-\frac{m{h}_g{a}_x}{2L}-\frac{m{h}_g{a}_y}{2B_r}$$(26)

$$ F_{zfr}=mg+\frac{mg{L}_r}{2L}-\frac{m{h}_g{a}_x}{2L}+\frac{m{h}_g{a}_y}{2B_r}$$(27)

$$ F_{zrl}=mg+\frac{mg{L}_f}{2L}+\frac{m{h}_g{a}_x}{2L}-\frac{m{h}_g{a}_y}{2B_r}$$(28)

$$ F_{zrr}=mg+\frac{mg{L}_f}{2L}+\frac{m{h}_g{a}_x}{2L}+\frac{m{h}_g{a}_y}{2B_r}$$(29)

The wheelbase  $$ L=L_f+L_r$$ .  $$ L_f$$  is the distance from the center of mass to the front axle and  $$ L_r$$  is the distance to the rear axle. The total vertical loads on the front and rear axles are  $$ \frac{mg{L}_r}{L}$$  and  $$ \frac{mg{L}_f}{L}$$ , respectively.

 $$ a_x$$ ​ denotes longitudinal acceleration.  $$ m{h}_g{a}_x$$  is the moment about the front/rear axle induced by longitudinal acceleration.  $$ \frac{m{h}_g{a}_x}{L}$$  represents the longitudinal load transfer due to acceleration.

 $$ a_y$$  denotes lateral acceleration.  $$ m{h}_g{a}_y$$  is the moment about the roll axis induced by lateral acceleration.  $$ \frac{m{h}_g{a}_y}{B_r}$$ ​​ represents the lateral load transfer due to cornering.

2.2. Select electric vehicle parameters

The vehicle model and selected vehicle parameters are shown in Figure 2 and Table 1

2.3. Analysis of simulation results

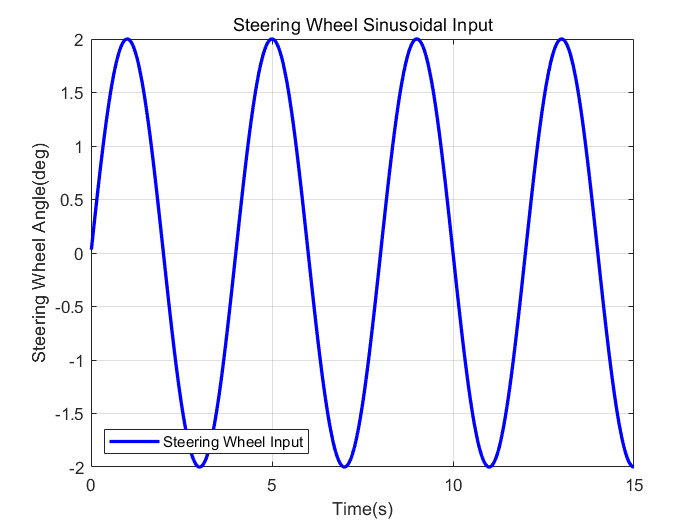
The simulation results of the vehicle at 30 m/s with sinusoidal steering wheel angle input (Figure 3) are shown in figure 4 and 5.

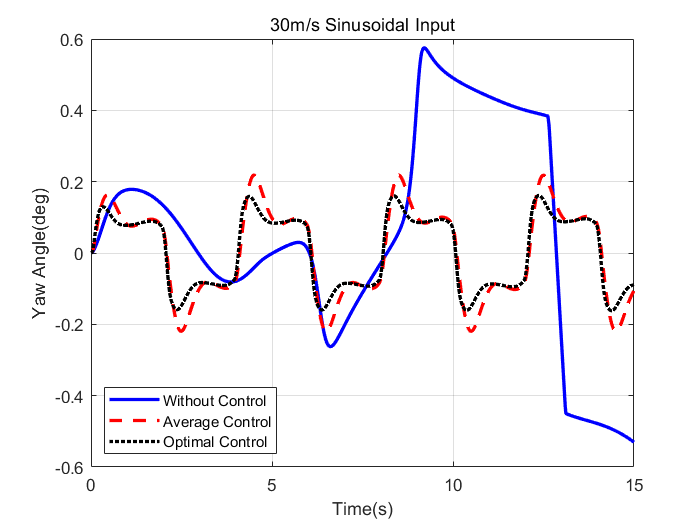
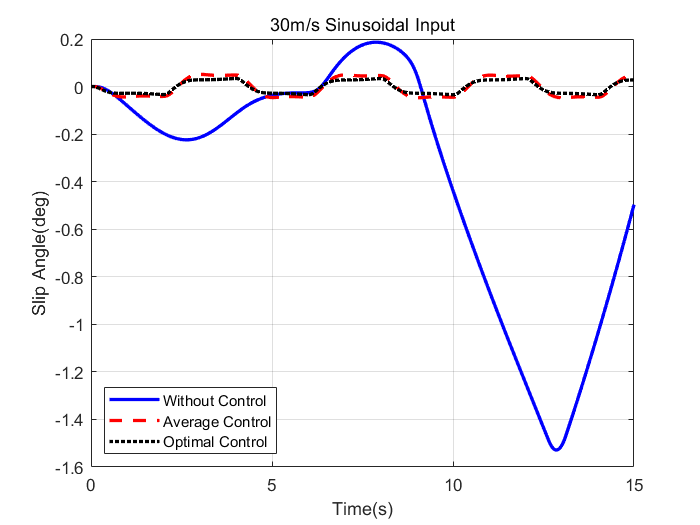
The experimental results under more working conditions are shown in Table 2 and Table 3.

Based on the data presented in Figures 4, 5 and Tables 2, 3, Under the optimal control, the maximum and RMS values of the vehicle's yaw angle and slip angle are significantly improved compared to those under average control and no control. This demonstrates that the optimal control effectively enhances vehicle stability and handling performance at speeds of 20 m/s and 30 m/s under both sinusoidal and delayed sinusoidal steering inputs.

However, the results indicate that the proposed algorithm does not achieve optimal control over the yaw angle RMS value in certain scenarios, such as at a speed of 10 m/s with sinusoidal or delayed sinusoidal steering inputs. Nevertheless, its impact on the yaw angle remains marginal, while the maximum value is substantially optimized. Therefore, it can still be concluded that vehicle stability is improved to some extent even under these conditions.

3. Conclusion

This study conducts a systematic analysis of torque distribution strategies for four-motor distributed drive vehicles, revealing the influence mechanisms of different control strategies on vehicle stability through theoretical modeling and simulation verification. The research establishes an optimal torque distribution model aiming to minimize the sum of squared tire load ratios. By incorporating constraints of total driving force and yaw moment, analytical expressions for four-wheel torques are derived using the Lagrangian multiplier method, and compared with the average distribution strategy and uncontrolled state. Simulation results show that under sinusoidal and delayed sinusoidal steering inputs, the optimal control strategy significantly enhances vehicle dynamic stability:

High-speed conditions (20–30 m/s): The maximum yaw angle is reduced by 58%–72%, and the root mean square (RMS) value is reduced by 58%–66%; the maximum sideslip angle is optimized by 93%–98%, and the RMS value is optimized by 89%–96%, effectively suppressing the risk of excessive yaw and sideslip during vehicle steering. Low-speed conditions (10 m/s): Although the optimization effect on the yaw angle RMS is limited (slightly increased in some scenarios), the sideslip angle is still optimized by 96%–99%, indicating the universal applicability of the optimal strategy for dynamic management of tire grip.

The study further finds that the average distribution strategy tends to cause uneven torque distribution under high-dynamic conditions due to neglecting differences in tire vertical loads. In contrast, the optimal strategy achieves collaborative optimization of driving force and yaw moment by introducing load weight coefficients, significantly improving tire friction utilization and energy efficiency.

In summary, the optimal torque distribution strategy effectively enhances vehicle handling stability and safety under most working conditions by dynamically adjusting four-wheel torques, providing a theoretical basis for the design of control algorithms for distributed drive vehicles. Future research can further integrate real-time road parameter sensing to optimize the robustness of the torque distribution model and adapt to complex driving environments.