1.  Introduction

Optical sensors play a crucial role in modern technology. Their unique photonic properties—such as resistance to electromagnetic interference, metal-free operation, and high integration—endow them with superior characteristics unmatched by other physical sensors. Among these, optical resonators stand out as the key structural elements for enhancing the sensitivity and selectivity of optical sensors. Due to the resonant behavior of photons, they exhibit ultra-high sensitivity, excellent monochromaticity, and outstanding imaging capabilities. These characteristics make optical resonators essential components in fields such as biology, chemistry, laser generation, optical imaging, and communications.

The current research focus is primarily on conducting comparative analyses of different types of optical resonators and their various properties, both horizontally and vertically. For example, the various properties of Fabry-Perot resonators (F-P cavities), whispering gallery mode resonators (WGM cavities), photonic crystal resonators (PC cavities), and plasma resonators are being studied. For instance, Li improved the detection limit for nanoparticles from the traditional 70 nm to 50 nm by studying microtube resonators in microtube Raman lasers [1]. Comparisons can also be made between properties such as quality factor, free spectral range, finesse, mode volume, coupling mechanism, and stability. For instance, Yang compared the quality factor and mode volume of different types of resonators, providing horizontal reference values for optical micro-resonators in application contexts [2].

This paper mainly compares the WGM cavities in optical resonators, i.e., the structures of micro-ring, micro-tube, micro-spheres, and micro-disks in terms of quality factor and other properties. The differences between horizontal and vertical comparisons are made through previous experimental data. The comparison can visualize the differences between different optical resonators and the different fields of application.

2.  Brief description of the optical resonator principle

Modern optical resonator cavities are divided into several main categories, including FP cavities, WGM cavities, PC cavities, and plasma resonators, among other major types. All resonators basically interfere with each other through the light beam itself, forming standing waves to achieve frequency selection and energy storage. This paper mainly introduces the principle of the FP optical cavity and the WGM optical cavity. The FP resonant cavity is the simplest and most important optical resonant cavity. Its main principle is to achieve the effect of its interference by reflecting the light beam back and forth between two parallel, smooth metal mirrors. The main criterion for selecting monochromatic light for the cavity is the phase difference between the beams, which is expressed by the phase difference formula.

(1)

The middle δ in the formula denotes the total phase difference of the light wave after one round trip inside the FP cavity, λ₀ is the wavelength of light in vacuum, n is the refractive index of the medium inside the FP cavity, and L is the distance between the two metal mirrors. The cavity transmittance can be expressed as the ratio between the transmitted light intensity and the reflected light intensity:

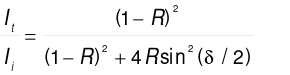(2)

where it denotes the transmitted light intensity, and I_idenotes the incident light intensity, where the FP cavity is considered to be an ideal optical cavity and the reflectivities of the two metal mirrors are the same, both are R. And when the frequency of the light beam in the cavity satisfies.

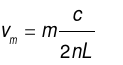(3)

(4)

where v_m is the resonant frequency of the beam in the final cavity and m is an integer. That is, a resonant beam is obtained when the optical range difference of the beam is an integer multiple of 2π and satisfies Equation (3) [3].

WGM cavities originally come from acoustic wave structures. After making a big splash in the optical field, the main structures are micro-ring, micro-tube, micro-spheres, and micro-disks. The refractive index of the inner and outer surfaces of WGM cavities is different, and the refractive index of the inside is higher than that of the outside, to achieve the total reflection effect. When the confined beam returns to the same point again after several total reflections, i.e., when the light propagates in the cavity after a circle and the light newly entering the cavity differs by an integer multiple of 2π in the optical range, a coherent resonance will be formed in the cavity. However, due to various microstructures, there are some differences in various properties [4]. The main sensing mechanisms of WGM cavities are dissipative sensing mechanisms and scattering sensing mechanisms. The dissipative mechanism is mainly used for the absorption loss of the object under the test, and the scattering mechanism is mainly used for the scattering phenomenon of light by the object under test. Scattering mechanisms are often used, including mode drift, mode splitting, and mode diffusion [5]. For example, a micro-ring resonator sensing mode is mode splitting, which consists of one or two waveguides and a closed ring resonant cavity, which is in the middle of two parallel waveguides, and the coupling region is where the resonant cavity meets the waveguide. The backward scattering of light interacting with nanoscale particles produces clockwise and counterclockwise modes. Compared to the original same resonant mode, CW and CCW are two resonant modes, i.e., mode splitting occurs. The beam is repeatedly cycled and continuously enhanced in the cavity to achieve increased light intensity and coherent interference and output from the coupling region [5, 6]. Of course, the principle of other microstructured resonators is roughly the same and can be viewed as the integration and superposition of multiple micro-ring structures.

3.  Main parameters of the optical microresonant cavity

3.1.  Quality factor

The quality factor is one of the important parameters of optical microresonators and is an important indicator of resonator loss.

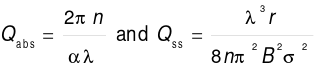(5)

In the above equation, Q_abs denotes the quality factor of absorption loss, which indicates the energy loss due to material absorption, α is the absorption coefficient, which indicates the ability of the cavity material to absorb light, λ is the wavelength of light in vacuum, and n denotes the refractive index. Q_ssis the quality factor of scattering loss, which denotes the loss due to the surface roughness of the material, r is the radius of the resonance cavity, σ is the surface roughness, and B is the correlation length. There are also coupling losses Q_coupl and radiation losses. The final expression for Q is given by.

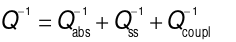(6)

The above equation does not take into account the radiation loss due to its small size. Also, the quality factor can be derived from the free spectral range.

(7)

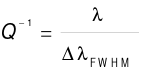(8)

In Equation (7), Δλ_FSR denotes the free spectral range, F denotes the fineness, and Δλ_FWHMdenotes the half maximum full width of the Lorentzian peak of a mode [7].

Since it is difficult to measure the quality factor of a single resonant cavity, which is usually measured together with an external waveguide, the concepts of loaded and intrinsic quality factors are introduced. The loaded Q is the actual measured value after taking into account all external coupling losses, while the intrinsic Q is the maximum theoretical value of the resonator without external coupling losses. Under different conditions and materials, the Q of each type of microresonator is different, and it is difficult to compare the same type of control variables with each other. Several studies have reported differences in Q values under different resonant cavity structures and materials. For example, an experiment using a 1.2-mm-long Si₃N₄microring resonator yielded a loading quality factor value of 4.5 × 10⁵ [8]. Another group of experimenters used thin-film lithium tantalate material to fabricate a microring resonator in which the loading quality factor was measured to be 2.7 × 10⁵ by the Lorentzian fitting method, and the intrinsic quality factor was calculated to be 8.4 × 10⁵ [9]. As another example, in the quality factor comparison of microtubular resonators, the quality factor of each resonator varies greatly. In the biosensor, the quality factor of a microcapillary structure with an external diameter of 100 μm and a wall thickness of 1 μm is as high as 8.6 × 10⁸, whereas in the temperature sensor, a silicone microtubular structure with an external diameter of 200 μm and a wall thickness of 15 μm has a quality factor of only 5.8 × 10³ [5]. Again, in the case of a microdisk resonator, for example, a microdisk resonator cavity with a diameter of 200 µm and different thicknesses has a measured intrinsic Q between 0.9 × 10⁶ and 1.5 × 10⁶ [10]. It can be seen that different materials, different resonator structures, different light wave frequencies, and different coupling methods will all cause significant differences in the quality factor. When evaluating performance, it is also necessary to consider the influence of various factors.

3.2. Free Spectral Range (FSR)

The FSR is defined as the frequency separation between two neighboring modes in the resonator spectrum.

(9)

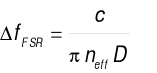(10)

where Δλ_FSR denotes the free spectral range in the wavelength domain, λ is the reference wavelength, n_eff is the effective refractive index, D is the radius of the resonant cavity, Δf_FSR denotes the free spectral range in the frequency domain, and c is the speed of light in vacuum. Improvement of the free spectral range is usually achieved by changing the cavity radius or the medium inside the cavity [2, 11].

3.3. Mode volume

The mode volume V represents the confined spatial parameter of the light in the cavity. It is defined as the ratio of the total spatial integral of the modal energy density in the resonant cavity to the maximum energy density.

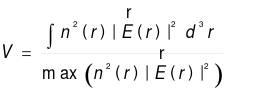(11)

The numerator represents the integral in overall space of the product of the square of the electric field vector at a point and the square of the refractive index, representing the integral of the overall electric field energy. The denominator represents the energy density maximum in the overall space. The size of the mode volume determines the performance of energy-demanding devices such as lasers [2, 11].

There are also other parameters, which are not repeated here, and different parameters need to be explored depending on the needs.

4.  Common application scenarios

WGM's high quality factor and small mode size allow it to be widely used in laser fabrication, micro-imaging, ultra-sensitive sensing, and optical communication. For example, micro-ring resonators are used in nanoscale particle imaging. The nanoparticles absorb pump light (light wavelength of 405 nm), which reacts and emits heat, causing the temperature of the surrounding medium, such as silica, to rise, further affecting the micro-ring. Under the combined effect of the expansion coefficient and thermo-optic coefficient of the micro-ring material, the optical range difference of the light beam inside the cavity increases, and resonance translation occurs. The photothermal signals on the surface of the micro-ring are then scanned by a galvanometer to generate a two-dimensional photothermal image. This imaging method does not require fluorescent labeling and has high detection sensitivity, which can be measured at room temperature, making it easier and more flexible than traditional imaging methods [12]. The excellent monochromatic selectivity of the optical resonator makes it a key part of laser fabrication. Micro-ring resonators are used as core components in LIDAR. Based on the vernier effect, the cascade of micro-ring resonators with different radii is used to expand the free spectral range of the laser, which enables the laser to emit light with different frequencies, and realize a wide wavelength tuning of ultra 170 nm on the Si₃N₄ platform, and also further enhance the scanning performance of the LIDAR through the thermo-optic and photovoltaic effects. A Kerr optical frequency comb is also generated through nonlinear effects to significantly enhance the radar ranging resolution [13].

The sensor direction has always been the main direction of application of microresonators. Utilizing the sensitivity of the microresonator to frequency, small changes are measured by frequency or wavelength shifts. For example, made of silicon dioxide 200 micron diameter microsphere resonator coupled with a 5-micron-diameter tapered optical fiber, through which water molecules and the microsphere surface bond, changing the refractive index, which in turn affects the transmitted power and wavelength shift to achieve the ability to measure humidity [14]. Of course, there have also been significant developments in biology and chemistry. The use of various proteins, DNA, or enzymes attached to the microresonator to change its characteristics has made a big difference in the fields of cell analysis, drug research, and biomolecular identification. In addition to changing the refractive index by attaching to the surface of the resonator, it is also possible to detect the intensity of transmitted light. Using a microtubular resonator with an inner diameter of 60 microns and a wall thickness of 8 microns, the nanoparticles enter the cavity and perturb the optical field in two ways, one way is for the particles to change the local dielectric constant in the cavity, which shifts the wavelength, and the other way is for the particles to scatter and cause a change in the transmitted light intensity. The signal-to-noise ratio is then improved by external Raman laser and laser external feedback (LHF) techniques to achieve the detection effect [15].

5.  Microresonator key technology

The main key technology and difficulty of optical resonators is to improve the quality factor, which is determined by a combination of many aspects, such as the choice of materials for the resonator cavity, coupling mode and efficiency, stability improvement, reduction of mode volume, and the preparation of the resonator cavity, the overall packaging process, and so on [16]. The next few aspects are briefly introduced.

5.1.  Material selection

Material selection is very important for microresonators in improving quality factor, coupling efficiency, and stability can be further improved by material selection. In chemical and biosensors, surface functionalized materials can significantly improve specificity, such as antibody modified for silicon oxide, through specific molecular recognition medium, non-selective physical adsorption is converted into targeted bioconjugation. The specificity can be significantly enhanced using this method, and the chemical composition of the covalent bonds is highly stable and resistant to cleaning. Another method with significant performance enhancement is to immerse the entire resonant cavity in a liquid core or droplet structure, where the light propagates within the liquid and the entire mode volume is also occupied by the liquid to be tested, at which point the interaction volume is thought to be tens of times higher than the entire interaction region for conventional surface swift field ratios. Liquid nuclei or droplet structures are suitable for live cell environments and volatile analyte detection. In the mid-infrared spectroscopy applications, there is a strong molecular vibration absorption in the Si-O bond of conventional silica, which leads to a sharp attenuation of the light energy and a limitation of the quality factor. And make ZBLAN zirconium fluoride glass, through the fluoride bond vibration frequency principle of the mid-infrared band, to avoid the shortcomings of the traditional resonant cavity. Therefore, it is possible to reduce the influence of light energy absorption according to the light wave frequency relative to the material vibration absorption frequency. In the electric field, piezoelectric crystals can be used, utilizing the electrostriction effect to trigger lattice deformation, leading to changes in the geometry and refractive index of the microresonator. In the magnetic field, a magnetostrictive composite material (Terfenol-D/PDMS) can be used, similar to the electrostriction in the electric field above, where the magnetic field also uses the magnetostrictive effect to deform the base. In addition, a variety of emerging materials, such as filipin and fish tooth proteins, have good bio-implantability, and plasma materials enhance sensitivity through localized effects [17].

5.2.  Coupling methods

In a WGM system, the laser is coupled into a resonant cavity, and then the intra-cavity light is coupled into an optical signal input device. Optical resonators are coupled in various ways, among which waveguide coupling is widely used. Waveguide coupling is mainly through the resonant cavity and external waveguides, such as optical fibers, integrated optical waveguides and other structures through the swift field penetration mode of coupling, swift wave coupling efficiency is higher, when the coupled waveguide and the micro-resonant cavity of the swift wave superposition and meet the matching conditions, can be better excitation of the WGM [18]. Fiber-optic coupling is one of the major categories of waveguide coupling. For example, in the coupling of a microsphere cavity to a waveguide, a D-type fiber optic coupler is used. Processing in a conventional fiber forms a structure suitable for embedding in the microsphere space. A common scheme is to prepare a D-shaped fiber and embed a certain structure in this fiber using FLMT. The fiber-optic coupling method also includes a tapered fiber coupler. This structure has three forms of optical paths, which increases the diversity of the beam traveling. The coupler is manufactured by laser ablation micromachining, and based on the MMF fiber end-etched cavity manufacturing method, the latter method is cheaper and easier to manufacture than the former. There are also various fiber coupling methods, such as a capillary fiber coupler, a hollow ring core coupler, and a multi-fiber face-based coupler [19]. There is also mutual coupling. Mutual coupling is a method of photon transfer through the superposition of abrupt fields between multiple resonant cavities, which is mostly used in cascade resonator systems. In addition, there are also early coupling methods, such as prism coupling, and emerging coupling methods, such as Non-Hermitian coupling, topological coupling, and nonlinear coupling.

5.3.  Stability of the resonator

The study of resonator stability includes mechanical vibration isolation, thermal noise control, and temperature fluctuation blocking. Mechanical vibration isolation refers to the reduction of frequency noise of optical resonators caused by vibration. Among them, mechanical vibration isolation can be divided into passive vibration isolation and active vibration isolation. Passive vibration isolation is used to reduce the vibration transmission efficiency through mechanical structure design, such as adding support points or elastic shims to absorb vibration energy. Active vibration isolation is realized through electromagnetic coils or piezoelectric ceramics to achieve real-time feedback control of platform movement, dynamic elimination of vibration interference. The thermal noise of resonators is Brownian noise, thermoelastic noise, and thermal refraction noise, of which Brownian noise is the main source of thermal noise. Thermal noise can be reduced by material selection, such as using low thermal expansion materials, low mechanical loss materials, and low-loss coating materials. Thermal compensation structures can also be designed to counteract thermal noise. Temperature fluctuations on the resonator are a phenomenon that occurs when the temperature changes in the cavity length and laser frequency. Mainly through the vacuum environment, multi-layer heat shielding, and high-precision temperature control technology to suppress the impact of temperature changes on the resonator. After the stability of the optical resonator is improved, the performance of all kinds of sensors will be greatly improved, such as laser gyroscope, laser interferometer, atomic clock, etc. The stability of the laser output frequency has been greatly improved, and the accuracy also rises [19].

6.  Conclusion

There are many research teams in the current scientific field, studying microresonators from various aspects and in various fields. This paper briefly introduces the WGM resonator by comparing and analyzing different WGM structures. Among them, structure design and material selection are the two factors that affect the performance of microresonators. Depending on the application scenarios, different approaches should be chosen to achieve a relatively ideal quality factor. If further discussion is needed, it is necessary to refer to other research papers. Future research on this component should combine the advantages of multiple disciplines to make up for the shortcomings of the existing optics, and a large number of experiments are needed to investigate the quality factor, mode volume and other properties of different materials, structures and coupling methods, which will provide more options for future applications. It is also necessary to actively apply various theoretical models in practice and constantly explore their potential for building society.