1. Introduction
With the rapid advancement of artificial intelligence (AI) technology, the automation and intelligence of robots are also advancing at an unprecedented pace, gradually enabling robots to independently accomplish tasks. While robots have already been deployed in factories, hotels, restaurants, and other settings, significantly enhancing operational efficiency and reducing labor costs, their mechanical structures' lack of flexibility and technological limitations currently prevent them from fully replacing humans in task execution. Achieving autonomous and precise grasping capabilities for robotic arms is a critical prerequisite for enabling independent task completion by robots. This capability not only facilitates intelligent picking and sorting operations but also promotes human-robot collaboration, eldercare services, and domestic assistance. Furthermore, it empowers robots to assist humans in hazardous environments such as fire scenes and earthquake zones, thereby enhancing safety.
The conventional method of pre-programming a mechanical arm's grasping path using fixed parameters lacks robustness and flexibility. Consequently, achieving precise and autonomous rapid grasping in unstructured environments is highly significant for the widespread application of robots and represents an essential function of intelligent robots. To realize this capability, it is necessary for the robot to perform pose recognition of the target object, determine specific parameters such as the grasping point, angle, and width of the gripper, and conduct path planning for the grasping process. Currently, research on autonomous grasping by mechanical arms predominantly focuses on integrating deep learning techniques with robotic manipulation. Autonomous and precise grasping is a critical prerequisite for enabling robots to independently complete tasks. This capability not only facilitates intelligent picking and sorting operations, thereby promoting the use of robots in human-robot interaction, elderly care, and domestic services, but also assists humans in executing tasks in hazardous environments, such as fire scenes or earthquake zones, thus enhancing safety [1]. pioneered the application of deep learning to address the robotic grasping problem in RGB-D views. The authors employed a two-stage cascaded system comprising two deep neural networks to enhance model performance. Grasping success rates of 84% and 89% were respectively achieved in experimental validations [2]. trained a fully connected network using RGB images of objects, achieving success rates of 79% and 74% on the training set and test set, respectively. However, the grasping accuracy exhibited certain limitations [3]. introduced the GG-CNN model, which significantly accelerated pose acquisition. Nevertheless, this model heavily relies on large-scale standardized labeled data, thereby limiting the optimization efficiency of the neural network [4]. employed GQCNN 4.0, GG-CNN, and its variants as expert models to construct an ensemble model, achieving a 6% improvement in accuracy on the Cornell dataset [5]. proposed a target grasping method that integrates the YOLO algorithm with the Soft Actor-Critic (SAC) algorithm. By incorporating incremental learning and transfer learning, they enhanced the efficiency of the proposed method. Currently, numerous algorithms and models have been improved based on the GG-CNN model. In this study, the Unet-DGN-L2 model was utilized for robotic arm autonomous grasping, effectively reducing computational complexity. Compared with the GG-CNN model on the public Cornell dataset, the accuracy increased by 17%, achieving a balance between lightweight design and high accuracy.
The primary focus of this research is the integration of a visual robot grasping target object pose estimation algorithm based on the Unet-DGN-L2 model. This encompasses the overall procedure and framework for visual robot grasping, the theoretical foundations of mechanical arm grasping combined with deep learning, enhancements to the UNet network, and experiments performed on the Cornell dataset. The study is organized into the following six sections: (1) The first section reviews the current mainstream methodologies for mechanical arm grasping in conjunction with deep learning, evaluates their strengths and limitations, and outlines the research direction of this paper. (2) The second section discusses prior work related to robot grasping, detailing the primary research directions in this field and providing an overview of the development of the Unet model. (3) The third section addresses the challenges that need to be resolved in robot grasping. (4) The fourth section presents a comprehensive description of the model architecture. (5) The fifth section analyzes and summarizes the experimental outcomes of the Unet-DGN-L2 model on the Cornell dataset. (6) The final section provides a concise summary of the overall research.
2. Related work
Machine grasping, as a critical subfield within robotics, has been the subject of extensive research. This article specifically focuses on the pose estimation of robotic arms in conjunction with deep learning methodologies. For a more comprehensive understanding of this domain, readers are encouraged to consult relevant reviews and scholarly articles [6,7]. In recent years, there has been a significant amount of research on robotic arm grasping combined with deep learning, and in terms of application scenarios, [8] proposed an algorithm for learning the probabilistic model of object geometry generation. In the scenario where the object is occluding, this model can identify the object based on the visible part of each object's contour, and then estimate the complete geometric shape of the object for grasping planning [9]. proposed a novel robot grasping pose prediction method Real-time Grasping Network (RGN). Taking KPConv as the backbone network, the prediction accuracy in complex scenarios is significantly improvedIn terms of grasping accuracy [10], used the RGB-D images of the scene to predict the optimal grasping posture. This model uses a deep convolutional neural network to extract features from the scene, and then uses a shallow convolutional neural network to predict the grasping configuration of the object of interest. It achieves an accuracy rate of 89.21% on the Cornell dataset, but the number of parameters is too large.
The Unet model can exhibit high accuracy with very few input training images. With its outstanding performance, Unet and the improved models based on it have been widely used in the medical field and achieved very good results [11].first proposed the Unet model and won the ISBI competition with a significant advantage by using this model [12]. proposed a neural network RIC-Unet (Residue-Inception-Channel attention-Unet) based on Unet for kernel segmentation. Techniques such as residual blocks, multi-scale and channel attention mechanisms are applied on RIC-Unet to segment the cores more accurately. This model achieved the third place in the Computational Precision Medicine Nuclear Segmentation Challenge.
3. Problem statement
During the grasping task of the robotic arm, the pose data of the grasped object must be obtained first. In this paper, the parallel gripper in the robotic arm is studied and represented using the following formula in the robot's basic coordinate system:
where
where
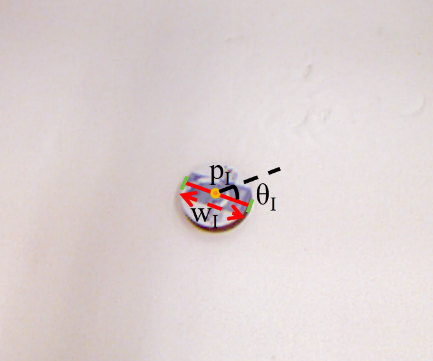
4. Methodology
4.1. Theoretical basis
The neuron layer of CNN’s (Convolutional Neural Network) network architecture consists of 3D - structured neurons with input spatial dimensions and a depth dimension. After receiving input, each neuron conducts linear transformation (e.g., scalar product) and nonlinear activation mapping. The network represents an end - to - end perception function parameterized by weights, with a category - related loss function at the network's end layer [14].
GGCNN(Generative Grasping Convolutional Neural Network) algorithm is a deep neural network model used to generate the grasping pose of a robotic arm. When predicting the grasping pose, the first step is to perform feature extraction and feature fusion on the input depth map to generate a probability map. Then, the grasping pose with the highest grasping probability is selected from the probability map for grasping. Specifically, the network of GGCNN consists of an input layer, a convolutional layer, a pooling layer and a fully connected layer. Among them, the convolutional layer learns the features of the input image, the fully connected layer classifies and regresses the features, and finally outputs the grasping pose information [15].
The convolutional layer is the core component of Unet and GG-CNN. The convolution operation calculates the dot product between the filter and the local area of the input by sliding the filter (also known as the convolution kernel) over the input data. This way, the spatial local features in the input data, such as edges and textures, can be captured [16], The expression of its convolution operation is:
where
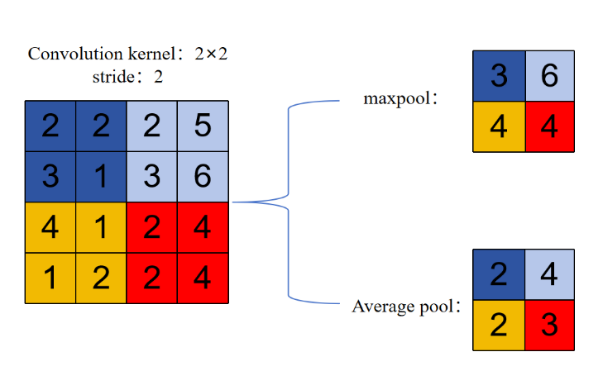
Another key layer is the Pooling layer. During the operation, it down-samples the input features to extract the features of the image. It uses several statistical functions to obtain the content on each window. There are two common pooling techniques: maximum pooling and average pooling [9],As shown in Fig. 2, max pooling selects the max value in the pooling area as output, retaining the most prominent features in the feature map and performing well in edge - area processing. Average pooling uses the mean function to smooth global content and reduce noise interference. This paper employs max pooling. The formula of the Max pooling layer is:
In this paper, the loss function adopted is the Mean Squared Error Loss function. It calculates the average value of the square of the difference between the predicted value and the true value. Since the error is squared, the output value is sensitive to large errors. Its mathematical expression is as follows:
Regularization techniques are often employed to prevent overfitting. Overfitting refers to the situation where a model overfits the training data, resulting in poor performance on new samples [9]. Regularization penalizes the complexity of the model by adding a regularization term to the loss function of the model. The addition of the regularization term and the loss function of the model will form a new objective function, and a better model can be obtained by minimizing this objective function. Its mathematical expression form is:
where
L2 regularization imposes constraints on the model parameters by introducing the square of the L2 norm of the weight parameters in the loss function as the penalty term. The formula is:
This regularization method helps prevent the model from overly relying on a few features or specific training samples. When there is no specific feature selection, It often performs exceptionally well, allowing all features to contribute to the model's prediction and thereby enhancing the model's generalization ability [16].
4.2. Dataset description
This paper adopts the Cornell dataset to verify the performance of the algorithm. At present, most of the papers on the grasping direction of robotic arms combined with deep learning are verified and evaluated using the Cornell dataset. Obviously, the adoption of this dataset is scientific. The Cornell dataset collects real-world scene data with the help of cameras, covering 240 categories of target objects. There are certain limitations on the target categories and quantities included in this dataset, which consists of 885 RGB images and an equal number of depth images. Each image is equipped with corresponding positive and negative capture labels, among which there are a total of 5,110 positive capture labels and 2,909 negative capture labels. Furthermore, the dataset provides the corresponding point cloud files for generating the corresponding depth images. As shown in Figure 3, some samples of the Cornell dataset are presented.

4.3. The proposed model
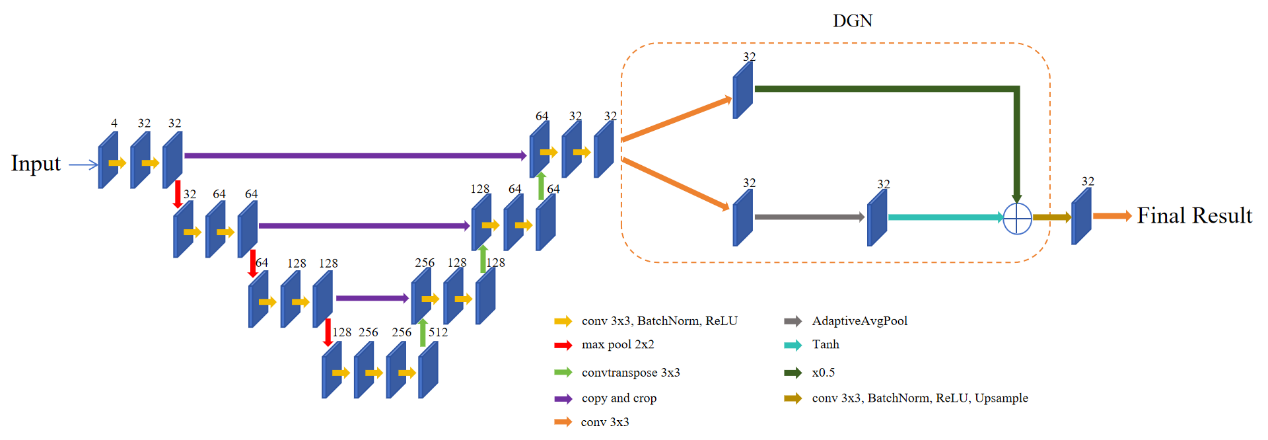
In this paper, aiming at the limitations of the pose estimation accuracy of visual robots in grasping target objects, the advantages of Unet, DGQN and L2 regularization are combined, thus the UNet-DGN-L2 model is proposed, for autonomous grasping of robotic arms. The Cornell dataset is adopted to prove the feasibility and effectiveness of this model, and its structure diagram is shown in Figure 4. Firstly, the input RGB-D image is processed by the Unet model. In the encoding stage, three downsampling operations are performed successively. Each downsampling includes convolution, normalization, and pooling processing. The convolution kernels used in the convolution operation are all 3×3. After each normalization processing, a linear correction unit ReLU is connected. Due to the use of filling processing, the size of the feature map remains unchanged before the downsampling pooling. The pooling window size and step size are both 2, so the feature map size is halved after the pooling operation. In the intermediate stage of encoding and decoding, three convolution, normalization and pooling processes are performed to further extract features. The convolution kernel used is also 3×3, and the size of the feature map remains unchanged in this stage. In the decoding stage, three up-sampling operations are performed successively. Each up-sampling includes deconvolution, convolution, and normalization processing. The convolution kernel used in the deconvolution operation is 3×3, which doubles the size of the input feature map. Convolution and normalization processing do not change the size of the feature map. After the Unet model is the DGN model, which drew on the literature’s DGQN module structure [13]. Combining the local field of view captured by the upper path of the DGN module with the global field of view captured by the lower path is more conducive to feature extraction by the model. Different from this, the DGN module here does not adopt the DWC lightweight grabbing network. In the final adjust layer after the DGN module, 3×3 convolution kernels are used for convolution and normalization processing, followed by the activation function ReLU. Finally, up-sampling is carried out through the bilinear interpolation algorithm to restore to the input image size. Finally, the feature vectors are mapped to their respective categories through convolution operations to obtain the output results. GGCNN is an end-to-end single-stage detection architecture. It has inherent limitations in capturing key information from small targets, and there is still room for improvement in its overall detection accuracy. However, Unet-DGN-L2 compensates for this drawback through the splicing and fusion of feature maps and the fusion of the global field of view and the local field of view in DGN.
5. Result and discussion
The experimental environment configuration is shown in Table 1. In this environment, we carried out the construction and training of the Unet-DGN-L2 model. After adopting the Cornell dataset, the weight and bias parameters of the Unet-DGN-L2 model were initialized as random values and input into the model. Operations such as convolution, pooling, and normalization were performed according to the network structure, and finally the output result was obtained. Compare the output value obtained by forward propagation with the real label and calculate the error. Based on the error results, the backpropagation algorithm is used to calculate the weights of each layer and the gradient of bias in order to update the parameters. Based on the results of the gradient calculation, the weights and bias parameters are adjusted using a learning rate of 0.001. Repeatedly carry out the above steps. After 300 training epochs, the training error meets the requirements.
|
Operating system |
Win11 |
|
PyTorch Version CPU GPU Batch size Number of learning rounds Optimizer Learning rate L2 regularization penalty coefficient Loss function |
torch2.7.0 Inter(R) Core(TM) i9 NVIDIA GeForce RTX 3070 T 2 300 AdamW 0.001 0.0001 MSE |
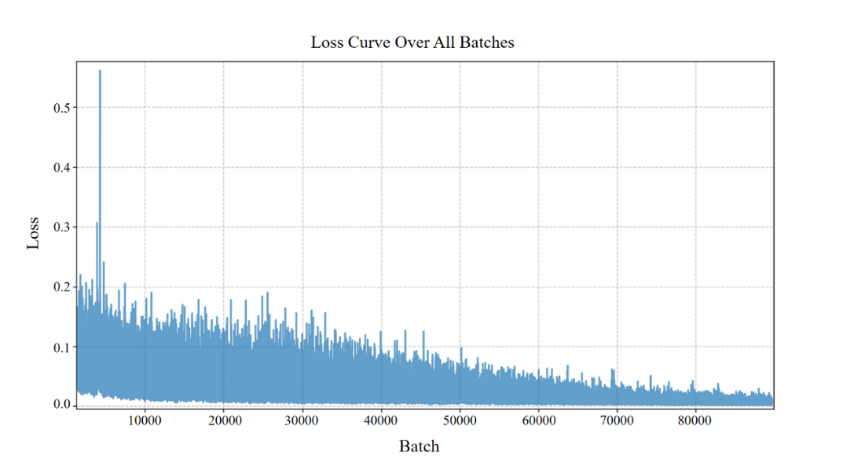
In this experiment, the Unet-DGN-L2 model is placed on the Cornell dataset for testing without data augmentation operations. The training results are shown in Figure 5, and the values of the loss function converge in the second half. In this paper, the standard rectangular metric is adopted to evaluate the model. Only when the difference between the generated grasping Angle and the correct grasping Angle is within 30° and the intersection and union ratio (IoU) score is greater than 0.25 can it be judged as a correctly generated grasping box. The mathematical expression is as follows:
where
In this experiment, the grasping block diagram generated by the Unet-DGN-L2 model is shown in Figure 6. The Unet-DGN-L2 model was compared with the GG-CNN model on the Cornell dataset, and the results are shown in Table 2. It can be found that the accuracy rate has increased by 17%, and it has increased by 13% compared with the improved GGCNN model. The experimental results prove that due to the stitching and the combination of local and global fields of view used in the Unet-DGN-L2 model, it is more conducive to feature extraction compared with GG-CNN, performs better in the dataset, and is more practical.
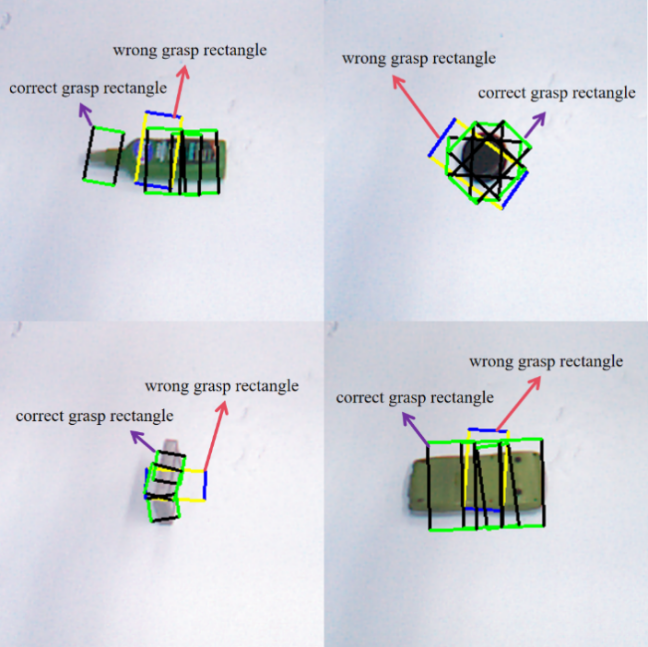
|
Network |
Accuracy |
|
GGCNN Improved GGCNN [15] Unet-DGN-L2 |
69% 73% 86% |
6. Conclusion
In this paper, a pose estimation algorithm for visual robots grasping target objects based on Unet are proposed, for the first time, and the Unet is introduced into the grasping pose estimation model successfully. And by cascading a lightweight DGN with a decoupled grasping network, the generation of the initial grasping rectangle was achieved. The experimental results on the public dataset Cornell show that this method has higher accuracy than the GG-CNN model, with an accuracy rate of 86%, and can predict a better grasping representation for robot grasping. This result indicates that the improvement on the Unet architecture is more efficient than the GG-CNN model, but there are still limitations in the model accuracy. In the subsequent work, we will study how to improve the success rate of the Unet model's grasping by improving it, and consider the autonomous grasping of the robotic arm combined with deep learning in a chaotic environment.
References
[1]. Lenz, I., Lee, H., & Saxena, A. (2014). Deep learning for detecting robotic grasps. arXiv: arXiv: 1301.3592. doi: 10.48550/arXiv.1301.3592.
[2]. Na, Y.-H., Jo, H., & Song, J.-B. (2017). Learning to grasp objects based on ensemble learning combining simulation data and real data. In 2017 17th International Conference on Control, Automation and Systems (ICCAS) (pp. 1030–1034). doi: 10.23919/ICCAS.2017.8204368.
[3]. Morrison, D., Corke, P., & Leitner, J. (2018). Closing the loop for robotic grasping: a real-time, generative grasp synthesis approach. arXiv: arXiv: 1804.05172. doi: 10.48550/arXiv.1804.05172.
[4]. Alladkani, F., Akl, J., & Calli, B. (2021). ECNNs: ensemble learning methods for improving planar grasp quality estimation. arXiv: arXiv: 2105.00329. doi: 10.48550/arXiv.2105.00329.
[5]. Chen, Y.-L., Cai, Y.-R., & Cheng, M.-Y. (2023). Vision-based robotic object grasping—a deep reinforcement learning approach. Machines, 11(2), 275. doi: 10.3390/machines11020275.
[6]. Jahanshahi, H., & Zhu, Z. H. (2024). Review of machine learning in robotic grasping control in space application. Acta Astronaut., 220, 37–61. doi: 10.1016/j.actaastro.2024.04.012.
[7]. Du, G., Wang, K., Lian, S., & Zhao, K. (2021). Vision-based robotic grasping from object localization, object pose estimation to grasp estimation for parallel grippers: a review. Artif. Intell. Rev., 54(3), 1677–1734. doi: 10.1007/s10462-020-09888-5.
[8]. Glover, J., Rus, D., & Roy, N. (2008). Probabilistic models of object geometry for grasp planning. In Robotics: Science and Systems IV. Robotics: Science and Systems Foundation. doi: 10.15607/RSS.2008.IV.036.
[9]. Li, X. Q., & Chen, Y. (2025). A method for predicting the grasping pose of a robotic arm in a cluttered scene. Mechanical & Electrical Engineering, 1–8.
[10]. Kumra, S., & Kanan, C. (2017). Robotic grasp detection using deep convolutional neural networks. In 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 769–776). doi: 10.1109/IROS.2017.8202237.
[11]. Ronneberger, O., Fischer, P., & Brox, T. (2015). U-net: convolutional networks for biomedical image segmentation. arXiv: arXiv: 1505.04597. doi: 10.48550/arXiv.1505.04597.
[12]. Zeng, Z., Xie, W., Zhang, Y., & Lu, Y. (2019). RIC-unet: an improved neural network based on unet for nuclei segmentation in histology images. IEEE Access, 7, 21420–21428. doi: 10.1109/ACCESS.2019.2896920.
[13]. Fu, K., & Dang, X. (2024). Light-weight convolutional neural networks for generative robotic grasping. IEEE Trans. Ind. Informat., 20(4), 6696–6707. doi: 10.1109/TII.2024.3353841.
[14]. O’Shea, K., & Nash, R. (2015). An Introduction to Convolutional Neural Networks. arXiv: arXiv: 1511.08458. doi: 10.48550/arXiv.1511.08458.
[15]. Zuo, S. W. (2023). Research on key technologies of robotic arm grasping based on deep learning and RGB-D data. Master’s thesis, Chang’an University.
[16]. Wei, Y. H., Chen, Y. C., & Gu, X. J. (2024). Fault diagnosis based on SincNet network combined with L2 regularization. Modular Machine Tool & Automatic Manufacturing Technique, 8, 158–162. doi: 10.13462/j.cnki.mmtamt.2024.08.031.
[17]. Cortes, C., Mohri, M., & Rostamizadeh, A. (2012). L2 regularization for learning kernels. arXiv: arXiv: 1205.2653. doi: 10.48550/arXiv.1205.2653.
Cite this article
Bao,X. (2025). Research on Pose Estimation Algorithm for Visual Robot Grasping Target Objects Based on Unet-DGN-L2. Applied and Computational Engineering,177,48-58.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of CONF-MLA 2025 Symposium: Applied Artificial Intelligence Research
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Lenz, I., Lee, H., & Saxena, A. (2014). Deep learning for detecting robotic grasps. arXiv: arXiv: 1301.3592. doi: 10.48550/arXiv.1301.3592.
[2]. Na, Y.-H., Jo, H., & Song, J.-B. (2017). Learning to grasp objects based on ensemble learning combining simulation data and real data. In 2017 17th International Conference on Control, Automation and Systems (ICCAS) (pp. 1030–1034). doi: 10.23919/ICCAS.2017.8204368.
[3]. Morrison, D., Corke, P., & Leitner, J. (2018). Closing the loop for robotic grasping: a real-time, generative grasp synthesis approach. arXiv: arXiv: 1804.05172. doi: 10.48550/arXiv.1804.05172.
[4]. Alladkani, F., Akl, J., & Calli, B. (2021). ECNNs: ensemble learning methods for improving planar grasp quality estimation. arXiv: arXiv: 2105.00329. doi: 10.48550/arXiv.2105.00329.
[5]. Chen, Y.-L., Cai, Y.-R., & Cheng, M.-Y. (2023). Vision-based robotic object grasping—a deep reinforcement learning approach. Machines, 11(2), 275. doi: 10.3390/machines11020275.
[6]. Jahanshahi, H., & Zhu, Z. H. (2024). Review of machine learning in robotic grasping control in space application. Acta Astronaut., 220, 37–61. doi: 10.1016/j.actaastro.2024.04.012.
[7]. Du, G., Wang, K., Lian, S., & Zhao, K. (2021). Vision-based robotic grasping from object localization, object pose estimation to grasp estimation for parallel grippers: a review. Artif. Intell. Rev., 54(3), 1677–1734. doi: 10.1007/s10462-020-09888-5.
[8]. Glover, J., Rus, D., & Roy, N. (2008). Probabilistic models of object geometry for grasp planning. In Robotics: Science and Systems IV. Robotics: Science and Systems Foundation. doi: 10.15607/RSS.2008.IV.036.
[9]. Li, X. Q., & Chen, Y. (2025). A method for predicting the grasping pose of a robotic arm in a cluttered scene. Mechanical & Electrical Engineering, 1–8.
[10]. Kumra, S., & Kanan, C. (2017). Robotic grasp detection using deep convolutional neural networks. In 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 769–776). doi: 10.1109/IROS.2017.8202237.
[11]. Ronneberger, O., Fischer, P., & Brox, T. (2015). U-net: convolutional networks for biomedical image segmentation. arXiv: arXiv: 1505.04597. doi: 10.48550/arXiv.1505.04597.
[12]. Zeng, Z., Xie, W., Zhang, Y., & Lu, Y. (2019). RIC-unet: an improved neural network based on unet for nuclei segmentation in histology images. IEEE Access, 7, 21420–21428. doi: 10.1109/ACCESS.2019.2896920.
[13]. Fu, K., & Dang, X. (2024). Light-weight convolutional neural networks for generative robotic grasping. IEEE Trans. Ind. Informat., 20(4), 6696–6707. doi: 10.1109/TII.2024.3353841.
[14]. O’Shea, K., & Nash, R. (2015). An Introduction to Convolutional Neural Networks. arXiv: arXiv: 1511.08458. doi: 10.48550/arXiv.1511.08458.
[15]. Zuo, S. W. (2023). Research on key technologies of robotic arm grasping based on deep learning and RGB-D data. Master’s thesis, Chang’an University.
[16]. Wei, Y. H., Chen, Y. C., & Gu, X. J. (2024). Fault diagnosis based on SincNet network combined with L2 regularization. Modular Machine Tool & Automatic Manufacturing Technique, 8, 158–162. doi: 10.13462/j.cnki.mmtamt.2024.08.031.
[17]. Cortes, C., Mohri, M., & Rostamizadeh, A. (2012). L2 regularization for learning kernels. arXiv: arXiv: 1205.2653. doi: 10.48550/arXiv.1205.2653.









