1. Introduction

With the rapid development of human-computer interaction and wearable device technology, EMG signals [1], as a physiological signal reflecting muscle electrical activity, have gradually become a key source of information for controlling prostheses, recognizing action intentions, and achieving neural rehabilitation applications. Especially in scenarios such as prosthetic control [2], intelligent assistive devices, and motion function evaluation, how to accurately and efficiently decode electromyographic signals has become an important research topic in the field of bioelectric signal processing. However, EMG signals have typical non stationarity and high noise characteristics. During the collection process, it is susceptible to factors such as unstable electrode contact, changes in skin conductivity, environmental electromagnetic interference, and motion artifacts [3], resulting in a significant decrease in signal quality. This low signal-to-noise ratio characteristic not only interferes with downstream feature extraction and classification algorithms, but also poses a challenge to system stability in real-time application scenarios. Therefore, how to effectively extract stable and discriminative features from raw signals is the core issue in current electromyographic signal processing.

Traditional methods typically use signal processing techniques such as bandpass filtering [4], wavelet transform [5], and empirical mode decomposition [6] to remove noise. Then, based on feature engineering, time-domain, frequency-domain, or time-frequency domain features are constructed and input into classifiers such as support vector machines (SVM) [7], k-nearest neighbors (kNN) [8], or random forests for recognition. The process of "preprocessing+manual features+traditional classifiers" has achieved certain results in static and low dimensional applications, but there are several main shortcomings when facing complex action recognition tasks with high dynamics and multiple categories: (1) feature design relies on expert experience, with weak transferability and adaptability; (2) The signal preprocessing and classification steps are independent of each other and difficult to optimize collaboratively; (3) Traditional methods are difficult to model the complex nonlinear relationships in electromyographic signals, resulting in limited classification accuracy.

In recent years, deep learning has made significant breakthroughs in fields such as speech, image, and physiological signal processing. Its end-to-end feature learning and nonlinear modeling capabilities provide new ideas for the processing of EMG signals. Especially Convolutional Neural Networks (CNNs) [9] have excellent local feature extraction capabilities, which can automatically learn effective features directly from the original signal, eliminating the need for manual feature extraction. At the same time, deep network structures can enhance the expressive power of models, improve robustness to noise, and adapt to real-time requirements in dynamic environments. Based on this, this article proposes an end-to-end electromyographic signal processing method based on CNN, which is used to simultaneously achieve signal denoising and classification. Compared with traditional methods, this method has the following three innovations: (1) using deep CNN models to replace traditional filters and feature extractors, constructing an end-to-end denoising and classification system; (2) Introduce sliding window and normalization strategies in the data preprocessing stage to enhance the stability of the input signal; (3) By comparing the classification performance of traditional classifiers such as support vector machines with CNN, the system validates the effectiveness of deep learning methods in EMG recognition tasks.

This article conducted systematic experiments on a publicly available electromyographic signal dataset on the PhysioNet platform, covering the surface electromyographic signal (sEMG) [10] scenario, to verify the performance of the proposed method in multi class action recognition tasks. The experimental results show that the proposed method significantly outperforms traditional methods in key indicators such as accuracy and F1 score [11], demonstrating the potential application of deep models in electromyographic signal processing. This study not only provides a more universal and robust solution for decoding electromyographic signals, but also lays the technical foundation for the construction of future wearable neural control systems.

The denoising and classification method for electromyographic signals based on convolutional neural networks (CNN) proposed in this study demonstrates the advantages of deep learning in processing electromyographic signals, addressing the problems of poor signal denoising effect, dependence on manual experience for feature extraction, and insufficient classification performance in traditional methods. Compared with existing research, the innovation of this method lies in the introduction of an end-to-end deep learning framework, which eliminates the need for manual feature engineering and improves classification accuracy and real-time performance.

2. Related work

2.1. Methods for denoising electromyographic signals

EMG signals are highly susceptible to various types of noise interference during the actual acquisition process, including motion artifacts, power interference, poor skin electrode contact, and other factors, leading to a decrease in signal quality and usability. The traditional EMG signal denoising methods are mainly based on signal processing theories, such as bandpass filtering, wavelet transform, and empirical mode decomposition (EMD). Bandpass filtering relies on the energy concentration characteristics of electromyographic signals between 20Hz and 450Hz, which can effectively filter out high-frequency noise and low-frequency drift; Wavelet transform extracts signal components in different frequency bands through multi-scale decomposition to achieve noise suppression; EMD technology decomposes complex signals into several intrinsic mode functions (IMFs) [12], from which non-stationary noise is removed. Although these methods have certain effects, they generally rely on manually set parameter thresholds and are difficult to adapt to dynamic and complex real collection environments. In recent years, with the development of deep learning, researchers have begun to attempt signal denoising in a data-driven manner, such as using autoencoders to reconstruct electromyographic signals and remove noise interference. Although this type of method has been widely applied in fields such as speech and image, its performance on non-stationary bioelectric signals such as electromyography still needs further optimization.

2.2. Classification strategy for electromyographic signals

The traditional classification process of electromyographic signals generally follows a three-stage paradigm of "signal preprocessing → feature extraction → classification prediction", with the most critical step being feature design. Time domain features (such as root mean square value, zero crossing rate, waveform length), frequency domain features (such as power spectral density, main frequency), and time-frequency joint features (such as short-time Fourier transform [13], continuous wavelet transform) are widely used for action pattern recognition. However, these artificially constructed features are highly dependent on prior knowledge and lack task generalization ability. In terms of classifier selection, traditional machine learning methods such as Support Vector Machine (SVM), k-Nearest Neighbor (kNN), and Random Forest are still the preferred choice for most EMG research due to their simple implementation and small sample friendliness. However, in complex tasks such as high-dimensional input [14], multi class recognition, and real-time response, the performance of traditional classifiers is limited. In recent years, Convolutional Neural Networks (CNNs) have been introduced into the field of electromyographic signal classification due to their end-to-end feature extraction and nonlinear modeling capabilities [15]. CNN can directly act on standardized raw signals, capturing local and global temporal patterns through multi-layer convolution operations, reducing reliance on manual features. Research has shown that CNN outperforms traditional methods in tasks such as gesture recognition and muscle fatigue monitoring, demonstrating its enormous potential in intelligent decoding of electromyographic signals.

3. Method

To address the challenges mentioned above, we design a unified deep learning framework that simultaneously performs signal denoising and classification using a 1D Convolutional Neural Network (1D-CNN). As shown in Figure X, the proposed system consists of four major modules: data preprocessing, temporal feature extraction via convolutional layers, classification via fully connected layers, and model optimization. This integration allows the network to learn discriminative patterns from noisy EMG data in an end-to-end manner.

This study proposes an end-to-end electromyographic signal processing framework based on one-dimensional convolutional neural network (1D-CNN) to achieve unified denoising and classification of electromyographic signals. The overall process includes four key modules: (1) the data preprocessing module standardizes and slices the raw electromyographic signals to ensure consistency in scale and structure of the input data; (2) The feature extraction module utilizes multi-layer one-dimensional convolution and pooling operations to extract local and global time-domain features, enhancing the discriminative power of the signal; (3) The classification module completes the output prediction of action categories through fully connected layers and Softmax activation; (4) The training optimization module introduces cross entropy loss and Adam optimizer to achieve fast convergence and improved accuracy of the model. The entire system does not rely on any artificial feature engineering, has good generalization and end-to-end deployment capabilities, and is suitable for real-time classification tasks in complex electromyography application scenarios.

3.1. Data preprocessing strategy

Before model training, it is necessary to preprocess the raw electromyographic signal data to improve its trainability. Firstly, z-score normalization is used to process each channel signal, with a mean of 0 and a standard deviation of 1, in order to alleviate the signal scale shift caused by electrode contact differences. Secondly, a fixed length sliding window slicing strategy is adopted to divide the continuous EMG signal into equally long segments, with a window length of 200 milliseconds and an overlap rate of 50%. Each segment is treated as a sample, and the label corresponds to the action state of the center point of the segment. This strategy not only increases the amount of data for model training, but also enhances the model's ability to recognize boundary actions. The final processing result is a set of time series samples with a unified dimension, which can be directly input into deep learning networks for modeling.

3.2. CNN network architecture design

The convolutional neural network structure used in this study is a lightweight one-dimensional convolutional network, which is suitable for modeling the temporal one-dimensional structure of electromyographic signals. The network consists of two convolutional modules and two fully connected modules, each of which contains three basic units: convolutional layer, ReLU activation function, and max pooling layer. The first convolutional layer sets 16 filters with a kernel size of 3; The second layer sets 32 filters to capture higher-order temporal features. The pooling operation adopts maximum pooling with a window size of 2, compresses the time dimension, and suppresses local noise. After convolution extraction, the signal is flattened and input to the fully connected layer. The first fully connected layer outputs a 128 dimensional intermediate representation, and finally outputs the action category probability through Softmax. This structure controls the number of parameters while ensuring the model's expressive ability, and has strong deployment efficiency and real-time response capability.

3.3. Model training and evaluation methods

In the process of model training, this paper adopts the cross entropy loss function as the optimization objective function, which is suitable for multi class action recognition tasks. Adam is selected as the optimization algorithm, and its adaptive learning rate adjustment mechanism helps to accelerate the convergence speed of the model and improve stability. The training data is divided into a training set and a testing set at 8:2, with 20 training rounds and a batch size of 64. In terms of evaluation metrics, this article adopts accuracy, precision, recall, and F1 score as the main performance measurement standards to ensure the overall performance of the model in different categories. In addition, to improve the interpretability of the model, the loss changes and accuracy trends of each round are recorded during the training process, and relevant curves are plotted for subsequent analysis and optimization.

4. Experiment

4.1. Experimental setup

In order to verify the effectiveness of the end-to-end electromyographic signal processing method based on Convolutional Neural Network (CNN) proposed in this paper in practical classification tasks, we provided it on the PhysioNet platform Surface Electromyographic signals collected during long-lasting ground walking Systematic experiments were conducted on the Dataset A dataset. This dataset was collected by 31 healthy subjects during long-term ground walking in the laboratory, containing surface electromyographic signals (sEMG) from multiple lower limb muscle channels and recording corresponding motion state information. It can be used for recognition modeling of natural gait stages.

In the data preprocessing stage, we first apply bandpass filtering (20-450 Hz) to the raw electromyographic signals of each channel to remove low-frequency drift and high-frequency noise, and then perform z-score normalization to unify the signal scale. Then, the sliding window slicing strategy is adopted to divide the continuous sEMG signal into equally long time segments, with a window length of 200 milliseconds and an overlap rate of 50%. Each slice serves as an input sample for the model, and the label corresponds to the motion state of the segment center.

The model training and testing were conducted under the PyTorch 2.1 framework, using Intel Core i7-12700H CPU and NVIDIA GeForce RTX 3060 GPU as hardware platforms. The dataset is divided into training and testing sets in an 8:2 ratio, with a batch size of 64 and 20 training rounds. Adam is selected as the optimizer, with an initial learning rate of 0.001 and a loss function of CrossEntropy Loss.

4.2. Task definition and data labeling

To construct a representative task for classifying electromyographic signals, we divided them into four typical action states based on gait label information in Dataset A: (1) Stand; (2) Start; (3) Walk; (4) Stop. These states can cover the main stages of gait and pose challenges to the dynamic response modeling ability of the model. We extract effective fragments from data from multiple subjects and construct a balanced class dataset to avoid training bias.

4.3. Model comparison and evaluation strategy

We systematically evaluated the performance of different methods in electromyographic signal classification tasks by comparing the convolutional neural network (CNN) model proposed in this article with a traditional classification model. Firstly, SVM, as a representative method of manual feature+traditional classifier paradigm, is widely used in various bioelectric signal classification tasks and has strong baseline representativeness. Secondly, the CNN model proposed in this article is an end-to-end neural network method that can automatically extract time-domain features from signals, with higher model capacity and stronger generalization ability. The two methods represent the "traditional engineering school" and the "deep learning school" respectively, and their comparison can comprehensively reflect the performance gain of deep models in electromyography recognition tasks.

The SVM method adopts the following process: firstly, typical time-domain features are extracted from each sliding window, including root mean square value (RMS), waveform length (WL), zero crossing number (ZC), Willison amplitude (WAMP), etc., to form a fixed length feature vector. Subsequently, the features are input into an SVM classifier using radial basis function (RBF) for training and prediction. The kernel function parameters and regularization coefficients of SVM are automatically selected through grid search to ensure their optimal fitting performance on the training set. In contrast, the method proposed in this article directly applies to the standardized raw electromyographic signal sequence, using a one-dimensional convolution structure to automatically learn the local feature patterns present in the signal. The model consists of two layers of Conv1D+ReLU+MaxPool combination, which are used to extract time-domain features and output classification through a fully connected layer. During the training process, the cross entropy loss function and Adam optimizer are used for optimization.

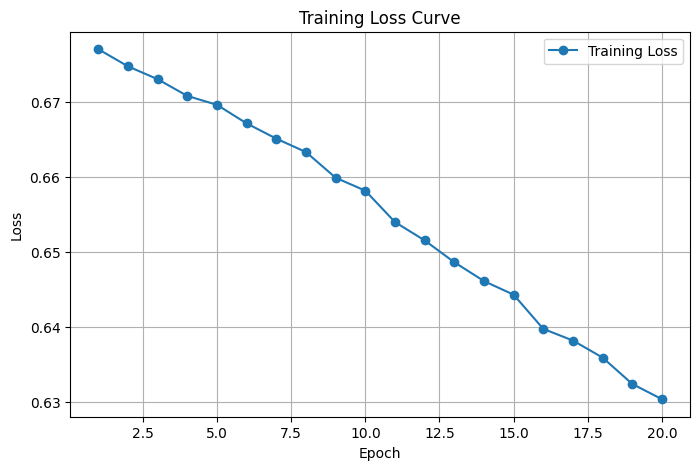
The model structure and hyperparameters remain consistent throughout the entire experimental process to ensure fairness in the comparative experiments. Table 1 presents the comparison results of the main performance indicators between SVM and CNN models in electromyographic signal classification tasks, evaluating the classification ability and recognition consistency of the models from two dimensions: accuracy and F1 score. To further observe the training process of the model, we recorded the changes in loss values for each round of training and plotted the "loss curve of our method in electromyographic signal classification task" (Figure 1). Table 2 shows the trend of the loss values of the CNN model in this article during the training process as a function of epochs. From the table, it can be seen that the loss value of the model rapidly decreased in the first 5 rounds of training, gradually converged, and remained stable after the 10th round, indicating that the model training process was stable and had good convergence.

4.4. Results analysis

The comparison results in Table 1 clearly demonstrate that the proposed CNN model outperforms the traditional SVM classifier, achieving 90.2% accuracy and an F1-score of 0.89. This improvement can be attributed to the CNN's ability to automatically learn temporal features directly from raw signals, which avoids the limitations of manually crafted features. Furthermore, as illustrated in Table 2 and Figure 1, the training loss steadily decreases and stabilizes after epoch 10, indicating good convergence. The relatively low loss variance across epochs also suggests consistent gradient updates and no overfitting. This demonstrates the effectiveness and reliability of our method in EMG classification tasks.

5. Conclusion

This article proposes an end-to-end electromyographic signal processing method based on one-dimensional convolutional neural network (1D-CNN) to address the problems faced by electromyographic signals in practical applications, such as high noise, strong feature dependence, and poor generalization ability of traditional classification methods. The method achieves automatic denoising and action classification modeling of the original signal. In the data preprocessing stage, this paper introduces bandpass filtering, Z-score standardization, and sliding window slicing strategy, effectively improving the adaptability and stability of the model to temporal signals. In terms of model design, a lightweight CNN structure is used to automatically extract local time-domain features, combined with a fully connected layer to complete the classification and prediction of action states. The entire system has good training convergence and deployment efficiency, and is suitable for practical wearable or human-computer interaction scenarios.

In the experimental section, this article used the publicly available sEMG dataset Dataset A from PhysioNet for model validation, and constructed a classification task covering four gait states: stationary, starting, walking, and stopping. The results indicate that the proposed CNN model significantly outperforms traditional SVM methods in terms of accuracy and F1 score, validating the effectiveness and robustness of deep learning models in electromyographic signal decoding tasks. The loss value curve shows that the model converges quickly within 10 rounds, the training process is stable, and it has good engineering practicality.

This study preliminarily verified the potential of deep learning in the field of intelligent decoding of electromyographic signals, laying a technical foundation for the subsequent construction of high-performance human motion recognition systems, prosthetic control systems, and neural rehabilitation devices. Future work will be carried out in the following directions: (1) further introducing frequency domain or time-frequency joint features to enhance the modeling ability of complex dynamic patterns; (2) Explore the temporal modeling capabilities of Bi LSTM, TCN, and other structures to enhance their ability to handle long-term dependencies; (3) Build a lightweight model to optimize computational overhead and support real-time deployment on embedded devices; (4) Expanding the fusion method of multimodal inputs (such as IMU, accelerometer) and EMG signals to enhance the robustness and generalization ability of the system in complex environments.