1.  Introduction

Guangxi, located in southwest China, is one of China’s provinces with the most frequent droughts and floods and relatively high temperatures. Qinzhou, specifically, is in the coastal area south of the Tropic of Cancer, where summer high temperatures are accompanied by concentrated and intense precipitation. Zhou Rui and colleagues identified Guangxi's landscape and concentrated rainfall from May to September as major factors contributing to floods [1]. Studies have shown that floods could bring about infectious diseases such as bacillary dysentery and influenza [2]; on a global scale, a crop production loss from 1982 to 2016 due to floods is estimated at 5.5 billion United States dollars [3]. On the other hand, temperature is another key meteorological indicator that influences plant growth, the ecological system, and human well-being. Thus, forecasting the precipitation and temperature could help safeguard inhabitants' property and health, as well as prevent reductions in grain yield.

Monthly precipitation and average temperature can be treated as time series. Time series forecasting involves constructing a model using past data. Time series forecasting has shown effectiveness in a large range of fields: propagation of diseases [4], meteorology [5], and the stock market [6]. This paper chooses Seasonal Autoregressive Integrated Moving Average (SARIMA) as the forecasting model to predict Qinzhou’s future precipitation and temperature based on past data from the National Oceanic and Atmospheric Administration (NOAA). First proposed by Box and Jenkins in 1976, the SARIMA model is a non-machine learning time series model that effectively captures seasonal patterns in time series with relatively few parameters [7]. Since both precipitation and temperature show strong periodicity (with values significantly higher in summer than in winter), the SARIMA model can aptly account for this pattern. This paper provides a method to forecast monthly average temperature with high accuracy and precipitation with medium accuracy in Qinzhou and points out this method's shortcomings when facing sudden changes in precipitation.

2.  Method

2.1.  Data collection

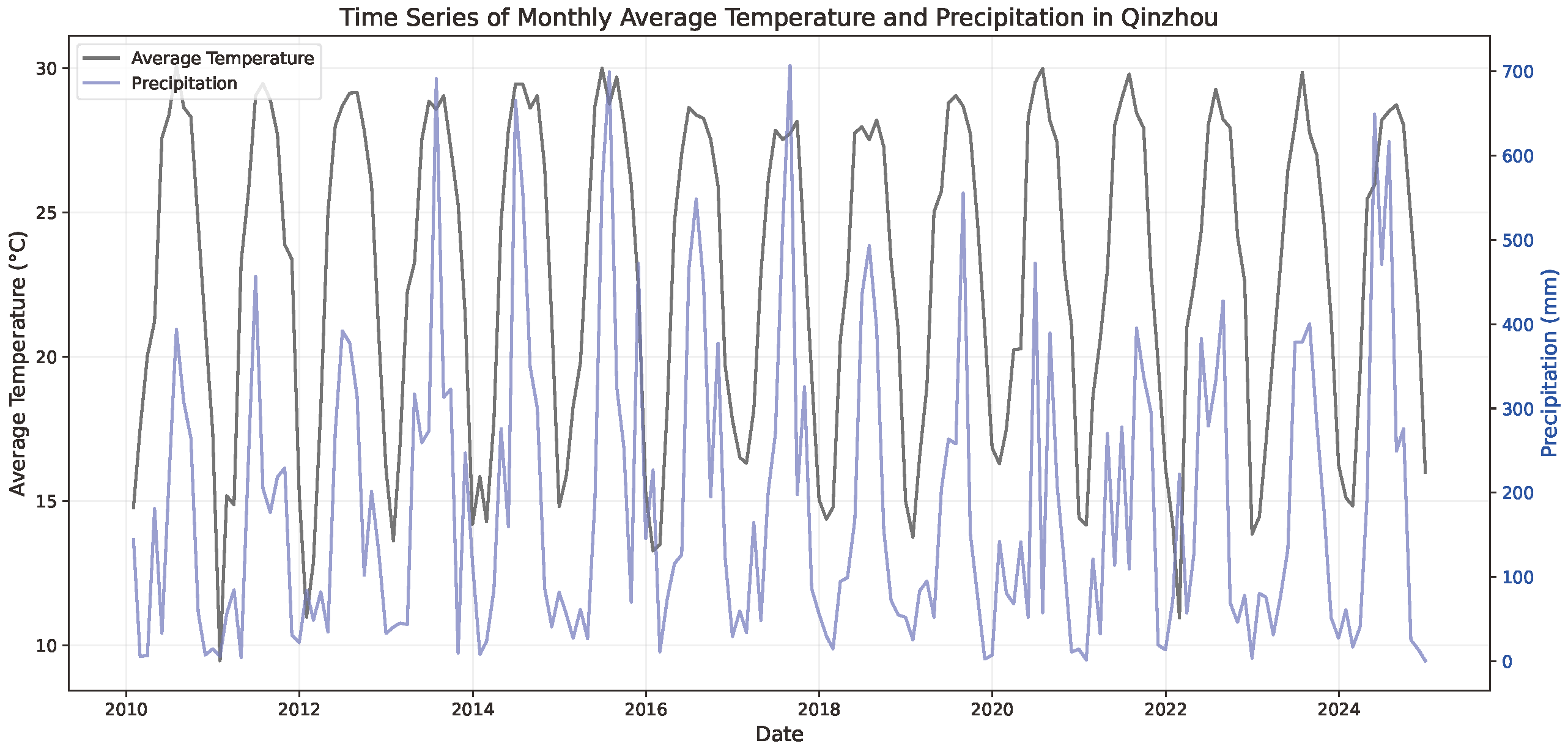
This paper uses public data from the Daily Global Historical Climatology Network (GHCN-DAILY) provided by NOAA [8]. The Qinzhou weather station has station ID CHM00059632. Both daily precipitation (element PRCP) in tenths of millimeters and average temperature (element TAVG) in tenths of degrees Celsius of the station are collected, spanning 2010 to 2024, 14 years in total. Daily precipitation and average temperature are aggregated into monthly data with units converted into millimeters and degrees Celsius, respectively. The time series plot is shown in Figure 1. Both datasets exhibit strong seasonality with a period of 1 year (12 data points), with peaks generally occurring in July. The first 12 years constitute the training set, while the remaining 2 years form the test set.

Compared to the average temperature, monthly precipitation in Qinzhou exhibits stronger fluctuations in summer. Specifically, in 2013, 2014, 2015, 2017, and 2024, the monthly summer precipitation in Qinzhou was significantly higher than that in other years.

2.2.  SARIMA

SARIMA model can be written as SARIMA(p,d,q)(P,D,Q)s; (p,d,q) as the non-seasonal order, (P,D,Q) as the seasonal order, and s as the period [7]. For models in this paper, s is set to 12, since monthly average temperature and precipitation of Qinzhou have periods of 12 months. The general formula of SARIMA model is

${\varphi }_p(L){\mathrm{\Phi }}_P(L^s)(1-L{)}^d(1-L^s{)}^D{y}_t=c+{\theta }_q(L){\mathrm{\Theta }}_Q(L^s){\epsilon }_t$(1)

where  $$ {\text{ϕ}}_{\text{p}}\text{(L)}$$  and  $$ {\text{Φ}}_{\text{P}}\text{(}{\text{L}}^{\text{s}}\text{)}$$  are the autoregressive polynomials;  $$ {\text{θ}}_{\text{q}}\text{(L)}$$  and  $$ {\text{Θ}}_{\text{Q}}\text{(}{\text{L}}^{\text{s}}\text{)}$$  are the moving average polynomials for non-seasonal and seasonal components, respectively;  $$ \text{L}$$  is the lag operator defined as  $$ \text{L}{\text{y}}_{\text{t}}\text{=}{\text{y}}_{\text{t-1}}$$ ; and c is a constant.

The process of determining the parameters can be summarized as follows: difference the time series until it becomes stationary to determine d, and traverse several parameter combinations, selecting the one that passes the Ljung-box test (LB test) with the smallest Akaike information criterion (AIC) values and good accuracy as indicated by the coefficient of determination ( $$ {\text{R}}^{\text{2}}$$ ). Failing to reject the null hypothesis of a LB test suggests the residuals in a model follow white noise distribution and are not autocorrelated; a model with higher accuracy and fewer parameters will result in a lower AIC value.

3.  Results and discussion

The Augmented Dickey-Fuller (ADF) test with the null hypothesis of non-stationarity is widely used to determine stationarity of time series. As shown in Table 1, since the ADF test p-values for the original monthly average temperature (0.1282) and precipitation (0.4120) series in Qinzhou are both greater than 0.05, d is set to 1, meaning the original series will be differenced once; the p-values of the differenced series are both 0.0000, confirming that the first-differenced series are stationary. ADF test p-values of both meteorological indicators' seasonal adjusted series are less than 0.05 (0.0008 for temperature and 0.0000 for precipitation). Thus, D is prioritized to be set to 0.

Aiming to find the model with the least AIC value, the parameters p, q, P, and Q were traversed from 0 to 3 for both time series, given that d=1, D=0, and s=12. The three combinations of parameters with the least AIC value are shown in Table 2, where * indicates the finally selected models. Due to the LB test p-value of the SARIMA model for Qinzhou monthly average temperature with the least AIC value being significant (less than 0.05), the SARIMA(2,1,1)(1,0,1)12 model with the second lowest AIC value and an LB test p-value of 0.0704 was selected. It was considered that when D=1, the SARIMA model with  $$ {\text{R}}^{\text{2}}$$  of 0.0741, 0.2360, and 0.2880, cannot effectively forecast Qinzhou monthly precipitation, the seasonal component is differenced once (D=1). Results are shown in Table 2. For monthly precipitation, all LB p-values are not significant, and thus the SARIMA(0,1,1)(0,1,2)12 model with the least AIC value of 1782.878 is selected. LB test p-values with lag 24 suggest that the residuals of the two selected models are white noise, and therefore, the two models have adequately captured both seasonal and non-seasonal patterns in the two time series.

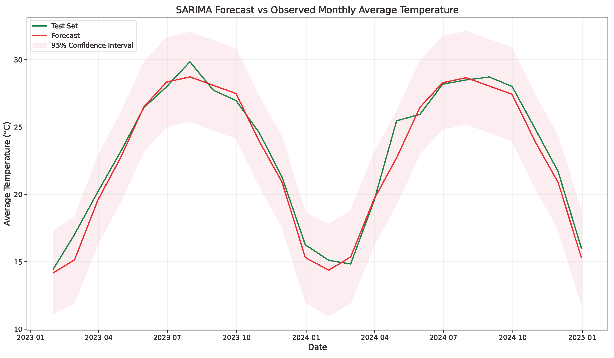
The SARIMA(2,1,1)(1,0,1)12 model has  $$ {\text{R}}^{\text{2}}$$  of 0.9691, which is very close to 1, and an RMSE of 0.8892°C, which is relatively low. Therefore, it can forecast Qinzhou's monthly average temperature with high accuracy. However, the SARIMA(0,1,1)(0,1,2)12 model exhibits limited explanatory power for the monthly precipitation in Qinzhou but still retains a certain degree of effectiveness, as shown by its  $$ {\text{R}}^{\text{2}}$$  of 0.5726 and RMSE of 125.2284 mm. These results can also be reflected in Figure 2 (a) and (b). By modeling the data from 2010 to 2024 with the same parameters, the SARIMA models' forecasts for Qinzhou monthly average temperature and temperature in 2025 and 2026 are shown in Figure 2 (c) and (d).

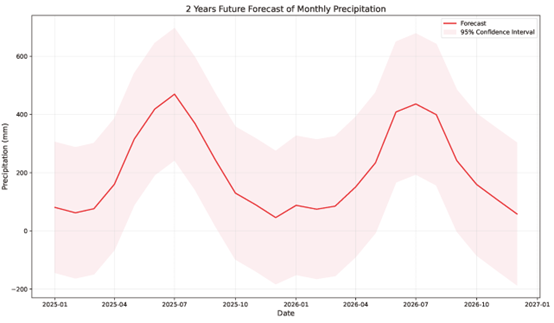
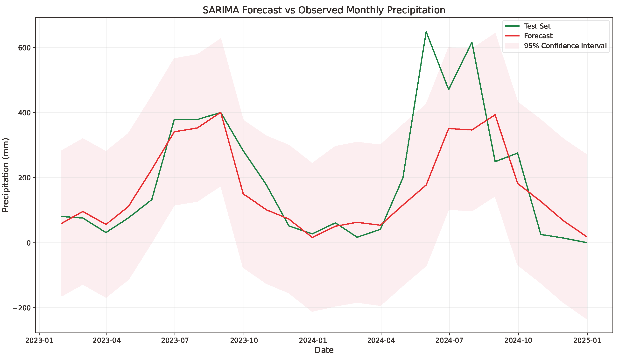
Figure 2. Forecast results

By examining the comparison plot of precipitation forecast and the test set (Figure 2 (b)), it is observed that the 95% confidence interval of forecast values captures the actual data of 2023. Additionally, the forecast values are shown to match the actual data with relatively high accuracy, suggesting that the SARIMA(0,1,1)(0,1,2)12 model effectively predicts the 2023 Qinzhou monthly precipitation; yet, in 2024, the actual data in May and July exceed the 95% confidence interval. As a result, the SARIMA model has an  $$ {\text{R}}^{\text{2}}$$  of 0.5726, in general. Qinzhou's monthly precipitation in May and July, 2024 (649.1mm and 616.6mm, respectively), reaches the highest value in the recent 7 years (monthly precipitation in August, 2024, is 706.9 mm). In May 18th and 19th, due to Synoptic-System-Related Low-Level Jet and Boundary-Layer Jet, Qinzhou experienced a rare extreme rainstorm, whose highest 1-hour precipitation broke Guangxi's past records [9]. This explains the mismatch of forecast values and actual values in May, while that in July may due to increased days with intense precipitation.

Compared to temperature, precipitation has features of greater temporal and spatial variations, and less stability, being concentrated in several successive days and susceptible to other meteorological elements such as monsoons, air pressures, and airflow convergences. Thus, precipitation has greater randomness and a higher probability of occurrence of extreme events. In light of these conditions, the SARIMA model exhibits its shortcomings when facing abrupt, extreme values of precipitation. Still, variations in forecast values of the SARIMA models can explain 57.26% of the variations in Qinzhou's monthly precipitation and 96.91% of the variations in Qinzhou's monthly average temperature, in 2023 and 2024. Hence, SARIMA models can provide valuable references for setting up precautionary measures against damage triggered by either high or low precipitation and temperature.

4.  Conclusion

This paper selected SARIMA(2,1,1)(1,0,1)12 and SARIMA(0,1,1)(0,1,2)12 to model the monthly average temperature and precipitation in Qinzhou from 2010 to 2022. AIC values and LB test p-values indicate that both models fit well. By comparing with actual data in 2023 and 2024, SARIMA models forecast monthly precipitation in 2023 and monthly average temperature in 2023 and 2024 with high accuracy, but due to external factors, as monthly precipitation in May and July 2024 reached the highest values in the past 7 years, the SARIMA model fails to capture this change. Since SARIMA models forecast based on past data, these results confirm that they are more applicable to time series with fewer abrupt, extreme fluctuations. Future studies could use the SARIMA with exogenous variables (SARIMAX) model by introducing data on atmospheric circulation and typhoons to address the shortcomings of the SARIMA model in forecasting extreme precipitation and achieve higher forecast accuracy.