1.  Introduction

Single-image Super-resolution (SR) aims to reconstruct a High-resolution (HR) image from its Low-resolution (LR) input, and this has become a fundamental task in computer vision. The applications such as digital photography, satellite observation, and film restoration increasingly need 4K or higher resolution imagery [1, 2]. In recent years, super-resolution methods which are based on deep learning have achieved excellent results on publicly available datasets [3, 4]. However, when applied to 4K-resolution large images, these methods often encounter Graphics Processing Unit (GPU) memory limitations and slow inference speed, and it is hard to deployment on real-world. A common method is tile-based inference, which large images will be divided into smaller patches to fit within GPU memory. However, simple stitching these tiles often create some visible seams at the boundaries, and this will lead to a discontinuity on the image, and degrade the perceptual quality of the reconstructed image [5, 6].

To address boundary artifacts, overlap-tiling with weighted blending has become a practical solution. It can make a seamless reconstruction while staying within hardware limits. Weighting profiles such as linear, cosine, and Gaussian windows reduce discontinuities by prioritizing the tile center and ignoring the edge [7]. These strategies have been widely adopted in large-scale segmentation and restoration pipelines [6]. However, during the experiment most existing evaluations of seamless SR assume the degradation model is ideal bicubic down sampling [8]. This assumption has an obvious difference from real imaging pipelines, because the inputs are frequently affected by blur degradations which may be caused by limited depth of field or camera shake or object movement [3, 9, 10]. Those degradations will bring uncertainty into reconstruction and interact with overlap-tiling strategies, but there is no systematically studying on this field [5].

This gap motivates this study. While seamless tiling has been explored, robustness to blur degradations under 4× SR at 4K resolution has not been systematically analyzed. Without any analysis, it is unclear that how overlap width, weighting profiles, and blur severity influence seam suppression, reconstruction fidelity. Filling this gap is crucial for the reliable deployment of SR systems in real-world [4].

This paper aims to propose a reproducible pipeline for seamless 4× SR on 4K images using a U-Net-style backbone with overlap-tiling and weighted blending. Two blending profiles—cosine, and Gaussian—are evaluated under multiple overlap widths, and Gaussian and motion blur at different strengths are synthesized to quantify robustness. There are three contributions: (i) presenting a practical seamless SR framework that removes boundary seams via overlap-tiling with weighted blending; (ii) conducting a systematic robustness study of seamless SR under Gaussian and motion blur; and (iii) providing an ablation study on overlap width and blending profile, then revealing the relationship between seam suppression, runtime, and degradation robustness.

2.  Method

2.1.  Dataset preparation

This study uses 20 HR natural images with resolutions up to 4K. These images serve as the ground truth for evaluating 4× SR. The dataset was designed to be simple but controlled, making it suitable for reproducible experiments.

To generate the LR inputs, two blur-based degradations were applied before down sampling. Gaussian blur with different standard deviations was used to simulate images that are out of focus, which often happens when the depth of field is limited in real photography. Motion blur was also synthesized with different lengths and directions to represent camera shake or object movement [5]. These two types of blur reflect the common degradations in real-world imaging conditions, which means images are rarely perfectly sharp [9]. After applying blur, the images were down sampled by a factor of four, producing LR inputs at one-quarter of the original resolution.

Each HR image produced two degraded LR versions: one with Gaussian blur and one with motion blur. In total, the dataset contains 40 LR images aligned with 20 HR references. The mapping between HR and LR images was recorded in metadata files to ensure reproducibility and consistency across experiments. All images were stored in uncompressed RGB format. And this design makes the dataset stable and reliable for systematic evaluation.

It is important to note that many super-resolution benchmarks use only bicubic down sampling as the degradation model [3]. While this approach is common, it does not capture the complexity of real-world imaging pipelines. By adding Gaussian and motion blur, this study creates a dataset that better reflects practical conditions.

2.2.  U-Net-based super resolution

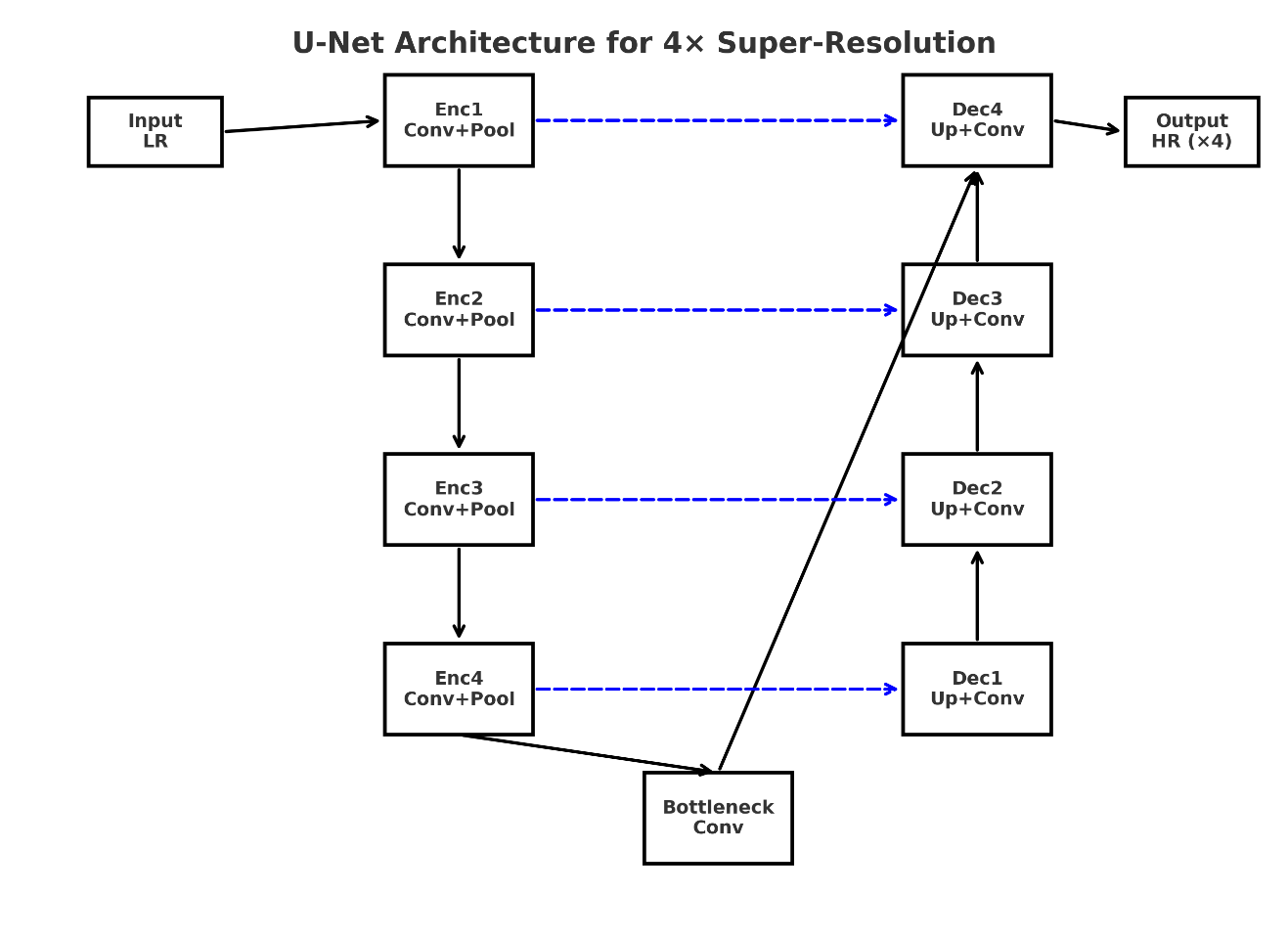
This paper adopts a U-Net-style backbone to perform 4× super resolution shown in Figure 1. U-Net is an encoder–decoder architecture which originally was introduced for biomedical image segmentation, but its design has proven effective in many restoration tasks [7]. The network consists of two main parts: an encoder on the left and a decoder on the right. The encoder reduces the spatial resolution of the input image through convolution and down sampling, then the decoder gradually up samples these features back to the target resolution. A key feature of U-Net is the skip connections, which directly transfer feature maps from each encoder stage to the corresponding decoder stage. These connections help preserve edges, textures, and fine structures.

In this study, the network takes a LR image tile as input and produces a HR tile as output. The use of tiles is necessary because 4K images are too large to be processed [4]. By dividing the input image into smaller tiles, the model can be applied to each tile independently. The skip connections make U-Net particularly suitable for this setup, because they help maintain continuity and local detail inside each tile.

Compared with heavier backbones such as GAN-based or Transformer-based networks, U-Net provides a balance between quality and efficiency. The architecture is lightweight, easy to train, and requires fewer computational resources, which aligns with the focus of this study on overlap-tiling and blending strategies rather than backbone design. The overall design ensures that the model can reconstruct sharp and consistent HR tiles that are later combined into seamless 4K outputs, as illustrated in Figure 1.

2.3.  Overlap-tiling inference and blending

Processing 4K images for super-resolution requires more GPU memory than is typically available. To handle this constraint, this study adopts an overlap-tiling strategy. Instead of using the entire image into the model, the input is divided into smaller tiles with overlapping borders. The overlapping regions ensure that boundary pixels are influenced by multiple tiles, which reduces discontinuities at patch edges [6].

To further improve seam suppression, weighted blending is applied in the overlapping areas. Two weighting profiles are evaluated in this study: The first one is Cosine (Hann) weighting, which applies a smooth sinusoidal transition from the tile center to the boundaries, producing gradual blending between adjacent tiles. The second is Gaussian weighting, which emphasizes the tile center more strongly with a Gaussian curve, and it offers a smoother decreasing near edges. These profiles are compared under different overlap widths to analyze how blending design affects seam suppression, runtime, and robustness.

In addition, robustness is tested under blur degradations. Gaussian blur kernels with varying standard deviations simulate defocus, while motion blur kernels with different lengths and orientations emulate object or camera movement [5]. These degradations are applied when generating the LR inputs, which allows the evaluation of how overlap-tiling and blending profiles behave when images deviate from the ideal down sampling [8].

2.4.  Evaluation metrics and experimental setup

The focus of this study is the evaluation of overlap-tiling and blending strategies rather than training a new backbone. Therefore, the U-Net model was applied in inference mode on prepared datasets without additional fine-tuning. Each test image was first down sampled with Gaussian or motion blur to produce LR inputs, as described in Section 2.1, and then super-resolved by a factor of 4× using the proposed pipeline.

A total of 20 HR images were used as references. Each HR image generated two LR versions: one with Gaussian blur and one with motion blur, resulting in 40 LR–HR pairs in total. These inputs were processed with two blending profiles (cosine/Hann and Gaussian) under multiple overlap widths.

The reconstructed images were evaluated using three criteria: Peak Signal-to-Noise Ratio (PSNR), which measures pixel-level fidelity; Structural Similarity Index (SSIM), which captures perceptual similarity; Runtime per megapixel (ms/MP), which quantifies computational cost.

These metrics together provide a balanced view of reconstruction quality, seam suppression, and efficiency. Results are reported as averages across the dataset to ensure fair comparison.

3.  Results and discussion

3.1.  Effect of overlap size on reconstruction quality 

This subsection evaluates how overlap size influences reconstruction quality under different weighting profiles. Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) are reported for Gaussian weighting and Hann weighting. These metrics reflect pixel-level fidelity and perceptual similarity.

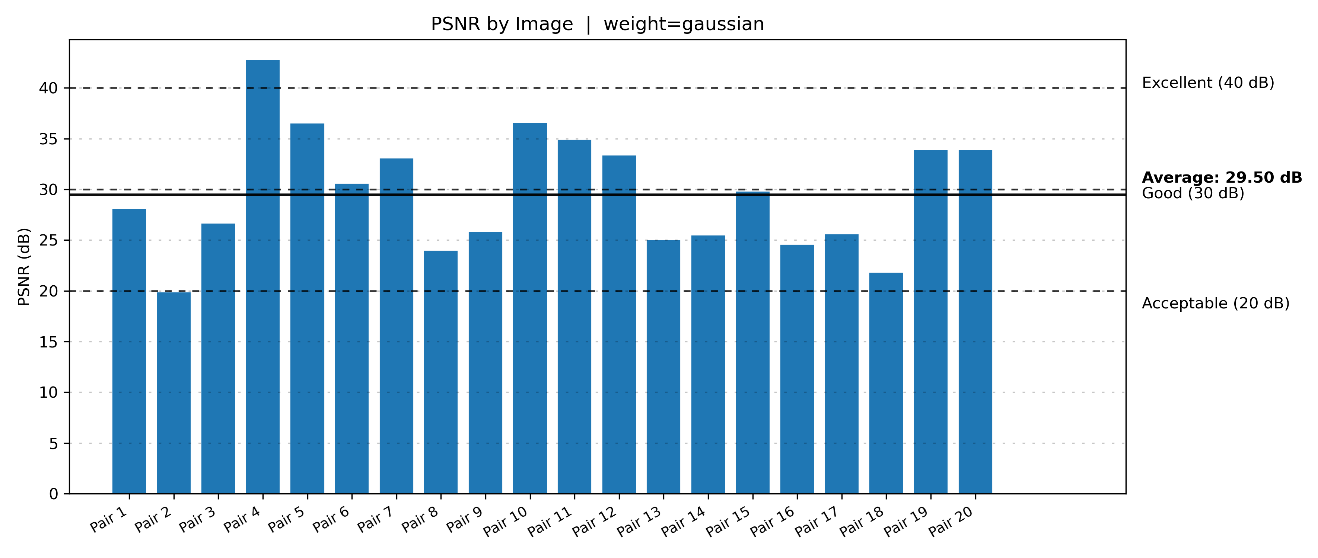
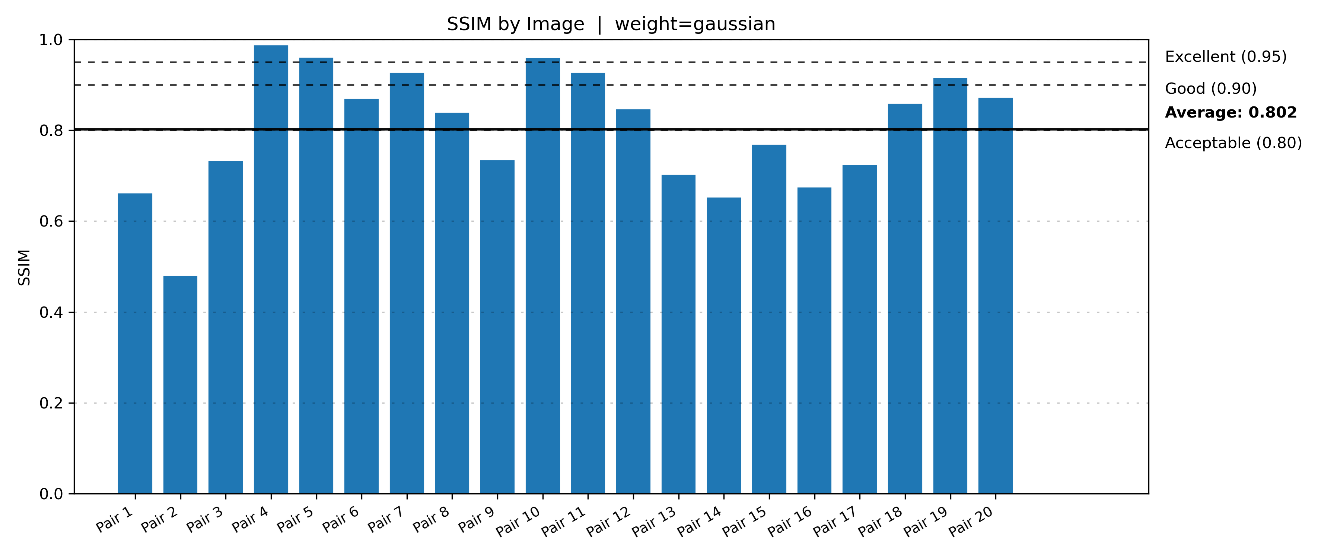
Gaussian weighting results are shown in Figure 2 and Figure 3. As the overlap increased, both PSNR and SSIM demonstrated consistent improvements. Larger overlaps allowed boundary pixels to be reconstructed using more contextual information, which suppressed visible seams more effectively. PSNR values ranged from about 20 dB to over 40 dB depending on the image pair, with an average above 29 dB. SSIM values often exceeded 0.90, confirming that Gaussian weighting preserved perceptual quality under different overlap settings.

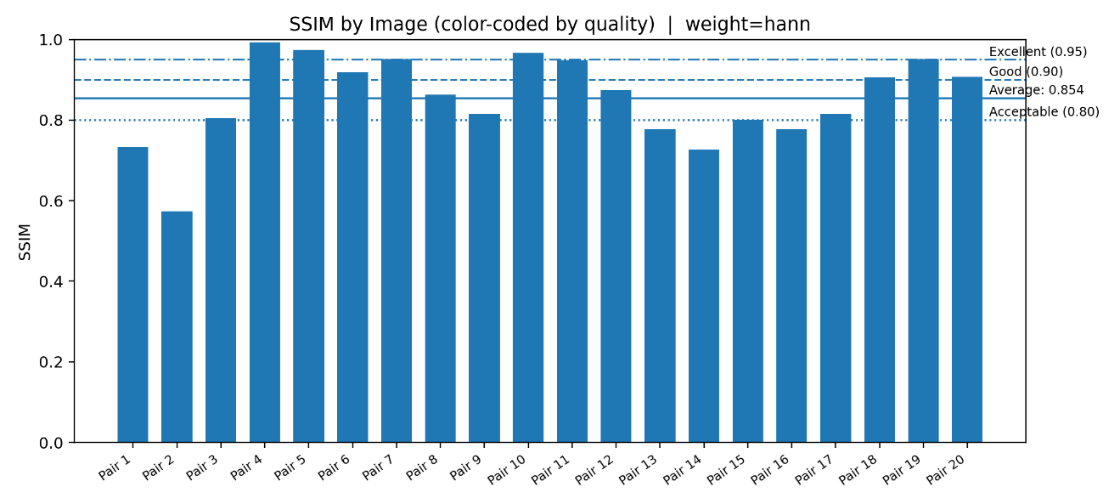
Hann weighting results are presented in Figure 4 and Figure 5. The average PSNR reached around 31 dB, which is slightly higher than Gaussian weighting. However, the SSIM values stabilized around 0.85, indicating that while Hann weighting improves pixel-level fidelity, it does not always enhance structural similarity to the same extent as Gaussian weighting. This suggests that Hann weighting produces sharper reconstructions but may not consistently capture perceptual continuity.

In summary, both weighting profiles benefit from larger overlaps. Hann weighting achieves slightly higher PSNR on average, while Gaussian weighting offers more stable SSIM performance. These complementary strengths motivate further analysis of quality distribution and robustness in the following sections.

3.2.  Quality distribution analysis

To evaluate reconstruction fidelity across different images and weighting strategies, both PSNR and SSIM quality distributions were analyzed. Table 1 summarizes the categorical distribution of PSNR and SSIM. The results show that 50% of reconstructions fall into the acceptable range (20–30 dB), while 42.5% are rated good (30–40 dB). Only 2.5% of the samples are classified as poor, and 5% achieve excellent quality above 40 dB. For SSIM, the majority of results are distributed in the poor and acceptable categories, with 35% and 27.5% respectively. Nevertheless, 37.5% of reconstructions reach good or excellent levels, indicating that seam suppression remains reliable in many cases.

Figure 6 compares PSNR distributions for Gaussian weighting and Hann weighting. The median PSNR for Hann (30.37 dB) is slightly higher than Gaussian (28.85 dB), suggesting that Hann weighting is more effective at maintaining consistent reconstruction quality. However, Gaussian weighting produces fewer extreme outliers, reflecting more stable behavior under challenging conditions.

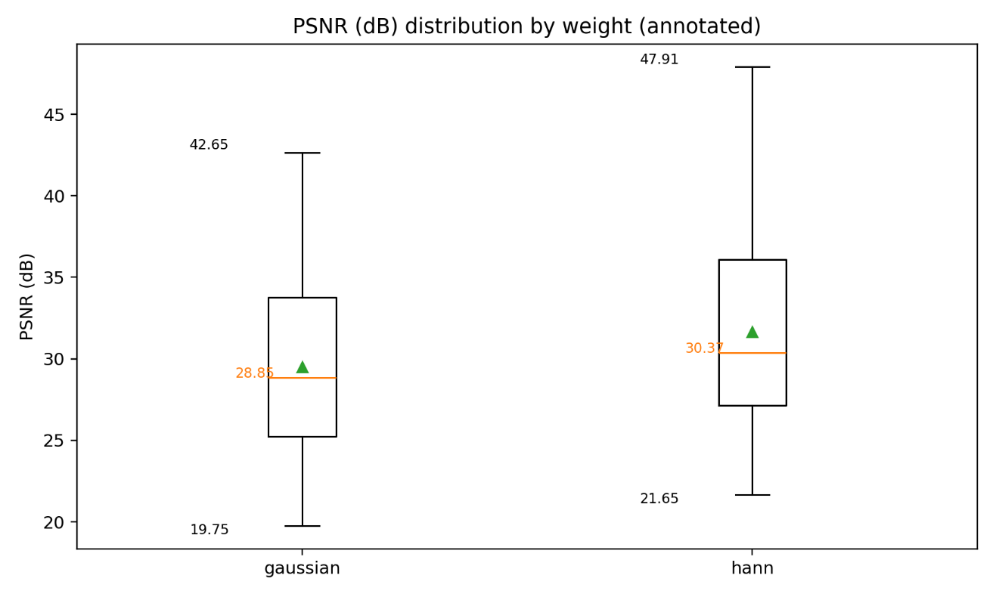
Figure 7 presents SSIM distributions for the same weighting functions. Hann weighting again shows a marginally higher median SSIM. At the same time, Gaussian produces a broader spread, with some reconstructions dropping below 0.6, which highlights its sensitivity to local variations. Still, both strategies are capable of delivering reconstructions above 0.9 in favorable cases.

Overall, the distribution analysis reveals that Hann weighting achieves slightly higher average fidelity, while Gaussian weighting provides a more balanced robustness. This complementary behavior motivates further examination of trade-offs between accuracy and computational efficiency in the following section.

3.3.  Trade-offs and practical insights 

In real-world super-resolution applications, a key challenge is the trade-off between reconstruction quality and computational efficiency. High-quality outputs usually require larger overlap and more complex weighting, but these settings also increase latency. On the other hand, faster configurations may reduce seams quickly but at the cost of lower PSNR or SSIM. Thus, identifying a balanced solution is essential for practical deployment.

Figure 8 shows the scatter plot of PSNR versus latency (ms per megapixel) for Gaussian and Hann weighting with overlap size 16. Both methods cover a wide range of quality levels, but Hann weighting tends to yield slightly higher PSNR for certain samples, while Gaussian shows more consistency in latency. This indicates that Hann may be more favorable when image fidelity is prioritized, whereas Gaussian is more predictable for time-constrained applications.

To further highlight optimal configurations, Figure 9 plots the Pareto frontier of PSNR against runtime across all tested settings. The Pareto points demonstrate that no single configuration dominates; instead, multiple optimal trade-offs exist. For example, some settings achieve excellent PSNR (>40 dB) but with increased runtime, while others offer moderate PSNR (~30 dB) at much faster speeds.

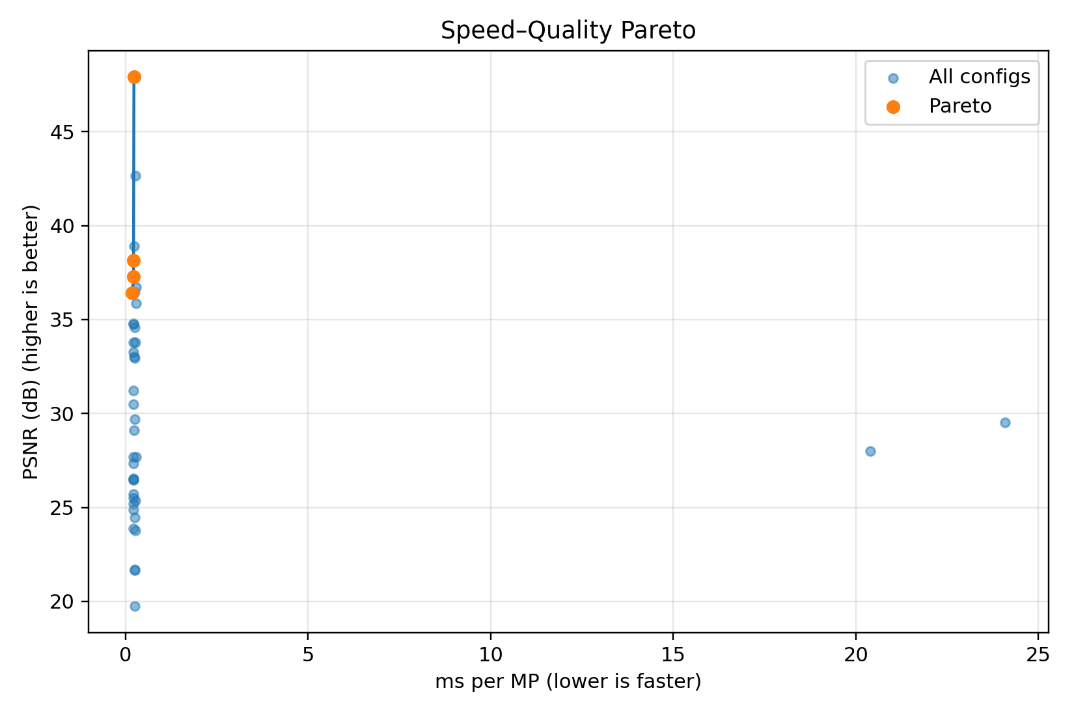
From these results, it can be concluded that the choice of overlap and weighting function should depend on deployment scenarios. For interactive or real-time applications, lower overlaps with Gaussian weighting may be sufficient.

3.4.  Robustness to Blur

Table 2 summarizes the results under Gaussian and Hann weighting when the overlap was fixed at 16 pixels. The metrics include PSNR, SSIM, and latency per megapixel.

The results indicate that Hann weighting is more robust to blur. Specifically, it achieves a higher PSNR (+2.2 dB) and better SSIM (+0.05) compared to Gaussian. The improvements are consistent with the observation that Hann weighting reduces edge artifacts and provides smoother transitions. However, this quality gain comes at the cost of slightly increased latency (about 0.19 ms/MP higher than Gaussian).

Overall, the comparison shows that Hann weighting offers a favorable balance when robustness to blur is a priority, while Gaussian remains attractive for scenarios where computational speed is more critical.

4.  Conclusion

This study proposed a reproducible pipeline for seamless 4× super-resolution on 4K images using a U-Net backbone with overlap-tiling and weighted blending. The experiments systematically evaluated Gaussian and Hann weighting under multiple overlap sizes and tested robustness against Gaussian and motion blur degradations. Results demonstrated that larger overlaps consistently improve seam suppression and reconstruction fidelity, while different weighting profiles offer complementary strengths, which is Hann achieved higher average PSNR and SSIM, whereas Gaussian showed more stable performance across varied conditions. Trade-off analysis further revealed that the choice of overlap and blending strategy directly impacts runtime efficiency. Overall, the findings highlight that overlap-tiling with proper weighting is a practical solution to mitigate boundary artifacts in high-resolution SR. This work provides both methodological insights and empirical evidence, contributing to the reliable deployment of SR in real-world imaging applications.