1. Introduction

With the growing adoption of Industry 4.0 and smart manufacturing, robots are increasingly deployed in industrial and logistics settings. In smart warehouses, sorting robots must perform dynamic path planning, precise package handling, and effective obstacle avoidance in highly uncertain environments, demanding strong adaptability, robustness, and real-time decision-making from control systems.

While model predictive control (MPC) has become a mainstream solution for trajectory tracking due to its constraint-handling and predictive capabilities, its fixed cost function weights—often tuned offline—limit its ability to dynamically balance competing objectives like tracking accuracy, obstacle avoidance, and energy efficiency under sudden disturbances. This restricts MPC's performance in dynamic applications.

Reinforcement learning (RL) offers a promising approach for adaptive control in complex environments. Although MPC-RL hybrid control has gained attention, most studies focus on learning system models or terminal costs, with limited exploration into real-time weight adaptation for multi-objective trade-offs.

To address this gap, this paper proposes a hierarchical RL framework that uses proximal policy optimization (PPO) to dynamically adjust MPC weights online, enabling sorting robots to autonomously prioritize control objectives in dynamic warehouse environments. The main contributions are:

1.A hierarchical MPC-RL framework with a PPO-based high-level agent for real-time weight optimization and an MPC low-level executor.

2.A state space incorporating tracking error and obstacle distance, along with a multi-objective reward function optimizing tracking, safety, and energy use.

3.Comprehensive Gazebo simulations demonstrating the method's superior tracking and adaptability compared to fixed-weight MPC.

2. Literature review

Currently, scholars worldwide are dedicated to robot control research, particularly in the field of nonlinear control, where continuous exploration aims to develop more efficient solution methods. For instance, Ma Linglong and Fu Lingfang [2] noted that various approximate solution methods—such as power series expansion and Galerkin sequential approximation—have emerged, providing theoretical foundations for handling the complex characteristics of nonlinear systems. These methods hold potential applications in robot dynamics modeling, enabling more precise descriptions of robotic motion states in complex environments.

In reinforcement learning algorithm research, the classical Q-learning algorithm proposed by Sutton and Barto [3] established a fundamental framework for robots to learn optimal policies through trial-and-error in their environments. Subsequent research has continuously optimized this approach, such as the Dyna-Q algorithm [4] combined planning and learning to accelerate learning speed. In the field of multi-agent reinforcement learning, Littman [5] provided theoretical support for decision-making in cooperative or competitive scenarios among multiple robots, enabling them to make rational decisions in complex interactive environments.

Despite these advances, challenges remain. The integration of nonlinear control and reinforcement learning requires deeper theoretical exploration to improve stability and convergence. Practically, reducing computational complexity while enhancing real-time performance is critical. This paper addresses these issues by integrating reinforcement learning with nonlinear control to improve robustness—a direction seldom explored. Unlike conventional methods confined to specific tasks, our approach leverages the adaptability of reinforcement learning and the precision of nonlinear control, offering a novel pathway for efficient robotic decision-making in complex, dynamic environments.

3. Research methodology

The core of this research is constructing a hierarchical reinforcement learning framework to achieve adaptive optimal control for sorting robots in dynamic warehouse environments. By decomposing complex decision-making into high-level strategic planning and low-level precise execution, this approach effectively resolves challenges faced by single reinforcement learning agents in high-dimensional, multi-objective decision problems, such as slow convergence and difficulty in exploration. This section details the framework's design, implementation of key components, and performance validation protocols.

3.1. Overall design of the hierarchical reinforcement learning framework

The proposed hierarchical control framework comprises two core levels: a high-level meta-controller and a low-level actuator. Its core principle is that the high-level agent learns to formulate "strategies" in complex dynamic environments—determining whether to prioritize tracking accuracy or obstacle avoidance based on the global state—while the low-level controller executes "tactics" by performing precise trajectory tracking and motion control according to directives from the high-level agent. Interaction between the two layers occurs through an interface defined as "weight adjustment commands."

The framework's workflow proceeds as follows:

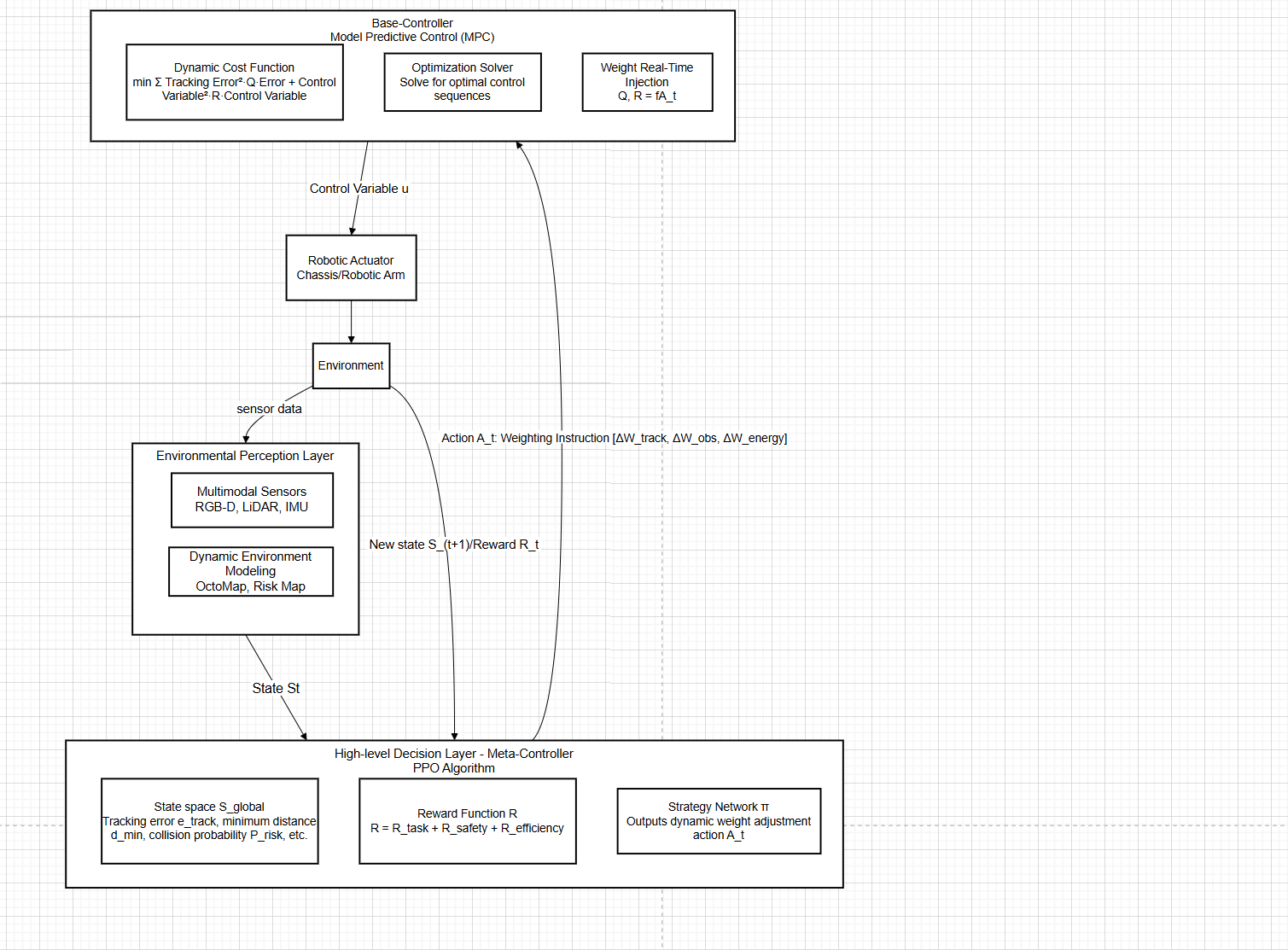
The system operates through a coordinated hierarchical structure. Multimodal sensors collect real-time environmental data, which is processed into a comprehensive state representation including robot pose, dynamic obstacle information, and target status. This state space incorporates key metrics like tracking error, minimum obstacle distance, and risk probability.

The high-level decision-maker utilizes a PPO-based policy network that processes this environmental state and outputs adjustments to the weight matrices in the MPC controller's cost function. These weight modifications serve as strategic instructions for dynamically rebalancing control objectives.

The underlying actuator is a Model Predictive Control (MPC) controller. It receives weight adjustment instructions from the higher level, maps them, and updates the weight matrices within its own optimization problem. Based on the current robot state and updated weights, the MPC re-solves the optimal control problem for the new sampling period, generating a sequence of optimal control commands for the future time domain. The first control command is then sent to the robot actuator for execution.

Environmental interaction completes the closed-loop cycle, generating new states and reward signals that feed back to the meta-controller for policy updates. Through continuous learning, the system progressively masters the dynamic balancing of trajectory tracking, obstacle avoidance, and energy consumption across varying operational conditions.

3.2. High-level meta-controller design

The high-level meta-controller employs a policy-based optimization reinforcement learning algorithm (PPO). Its function is to serve as an adaptive decision unit that perceives dynamic environmental changes and outputs adjustment instructions for the parameters of the underlying controllers.

State Space Design:The high-level state space (S_high) must contain sufficient global information to support strategic decision-making. Its design is as follows:

$S_{high}=\{e_{track},d_{min},v_{obs},P_{risk},E_{bat}\}$

Where:

$e_{track}$ The Euclidean distance between the current robot position and the target point on the reference trajectory, reflecting tracking accuracy.

$d_{min}$ The distance detected by the LiDAR between the robot and the nearest dynamic obstacle, directly indicating safety risk.

$v_{obs}$  Approach velocity of the nearest obstacle, used to predict evolving risk trends.

$P_{risk}$ The path collision probability estimated via Bayesian filtering (e.g., particle filtering), derived from the risk map, quantifies environmental uncertainty.

$E_{bat}$ The percentage of remaining battery power in the robot, providing a basis for energy efficiency optimization.

Action Space Design:

High-level actions A_highare not direct control inputs but adjustment instructions for the weight parameters of the lower-level model predictive control (MPC) cost function. This constitutes a continuous action space:

$A_{high}=[\mathrm{\Delta }{W}_{track,}\mathrm{\Delta }{W}_{obs,}\mathrm{\Delta }{W}_{energy}]$

Where $\mathrm{\Delta }{W}_{track,}\mathrm{\Delta }{W}_{obs,}\mathrm{\Delta }{W}_{energy}$ represent the weight adjustment quantities for the tracking error term, obstacle avoidance term, and energy consumption term in the MPC cost function, respectively. These adjustment quantities are mapped to the actual weight parameters of the MPC through a linear transformation layer, enabling direct and smooth regulation of the underlying control by the high-level strategy.

Reward Function Design:

The high-level reward function $R_{high}$ aims to guide the agent in learning multi-objective trade-off strategies, employing a composite reward design:

$R_{high}=\alpha 1\cdot R_{task}+\alpha 2\cdot R_{safety}+\alpha 3\cdot R_{efficiency}$

The specific components are as follows:

Task Reward $R_{task}$: If successfully grabbing a package: $R_{task}=+100$, Task delay penalty ($t_{delay}$ is the delay time): $R_{task}=-10\cdot t_{delay}$.

Safety Reward $R_{safety}$: If collision occurs $R_{safety}=-50$, apply continuous penalties when $d_{min}$ falls below the safety distance $d_{safe}$. At this point, $R_{safe}=-max(0,20\cdot (d_{safe}-d_{min}))$ .

Efficiency reward $R_{\text{efficiency}}=-0.05\cdot {\sum }_t\parallel u_t{\parallel }^{\wedge }2$: Penalizes the square of the control action to reduce energy consumption.

Here, $\alpha 1,\alpha 2,\alpha 3$ is a hyperparameter used to balance the priorities of different objectives.

3.3. Underlying actuator design

The underlying actuator consists of a Model Predictive Controller (MPC). It receives weight parameters from the higher layer and generates precise, smooth, and constraint-satisfying control commands.

MPC Optimization Problem Formulation:At each sampling time step k, the lower-level MPC solves the following finite-time domain optimization problem:

$\min {\sum }_{i=0}^{N-1}(\parallel x(k+i\mid k)-x_{ref}(k+i){\parallel }^{\wedge }{2}_{Q(k)}+\parallel u(k+i\mid k){\parallel }^{\wedge }{2}_{R(k)})$

$\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}x(k+i\mathrm{\mid }k)=f(x(k+i\mathrm{\mid }k),u(k+i\mathrm{\mid }k)),x_{min}\le x(k+i\mathrm{\mid }k)\le x_{max},u_{min}\le u(k+i\mathrm{\mid }k)\le u_{max}$

A key innovation lies in the weight matrices Q(k) and R(k) no longer being fixed. Instead, they vary over time k and are dynamically adjusted by the upper-level agent based on the output $A_{high}$ at each control cycle. For instance, when the higher-level agent detects high risk ($d_{min}$) and low safety ($P_{risk}$), it increases the weight of the corresponding control variable in R(k) or adjusts Q(k) to prioritize obstacle avoidance, making the robot more "cautious." In safe environments, it restores the optimization to balance tracking accuracy and energy consumption.

4. Experiments and results analysis

To validate the effectiveness of the proposed hierarchical reinforcement learning-based dynamic weight model predictive control method, this section designs detailed simulation experiments and compares them with traditional control methods. All experiments were conducted on a hardware platform equipped with an Intel i7-12700H CPU and NVIDIA RTX 3060 GPU, running Ubuntu 20.04 LTS, ROS 2 Foxy, and Gazebo 11.

4.1. Experimental setup

4.1.1. Simulation environment and scenario

Experiments were conducted in a simulated 10m×10m warehouse scenario. This environment included static obstacles (shelves, cardboard boxes) and three dynamic pedestrian obstacles moving at random speeds between 0.3–0.8 m/s (their paths generated online by the RRT algorithm). The robot's task was to start from a fixed origin, follow a predefined global path, and sequentially reach three target workpoints.

4.1.2. Comparison methods

For comprehensive evaluation, three classical control methods were selected as baseline comparisons:

1. Fixed-Weight MPC (F-MPC): An MPC controller employing a fixed weight matrix meticulously tuned manually, which performs optimally in interference-free environments.

2. PID Controller: A classic PID trajectory tracking controller supplemented by a global path planner.

3. HRL-MPC (Proposed Method): Dynamically adjusts MPC weights using the hierarchical reinforcement learning framework introduced in Chapter 3.

4.1.3. Evaluation metrics

The following four quantitative metrics are used for evaluation:

1. Average Tracking Error: The mean Euclidean distance between the robot's actual trajectory and the reference path.

2. Mission Completion Time: The duration from the starting point to reaching the final target point.

3. Collision Count: Number of collisions with obstacles.

4. Energy Consumption: Use the integral of the control variable's quadratic form$\int (u^{T}u)dt$ as a proxy indicator.

4.2. Results and discussion

4.2.1. Overall performance comparison

To obtain statistically valid results, each method was tested across 20 randomly generated dynamic scenarios. The statistical results (mean ± standard deviation) of performance metrics are shown in Table 1.

In terms of tracking accuracy, the average error of HRL-MPC was 48.0% and 29.3% of the F-MPC and PID methods, respectively, significantly outperforming the comparison methods.

In terms of efficiency, HRL-MPC achieved the shortest task completion time, reducing it by 14.0% and 28.2% compared to F-MPC and PID, respectively.

Regarding safety, HRL-MPC avoided collisions in all 20 experiments, whereas F-MPC and PID methods experienced 2 and 7 collisions, respectively.

In terms of energy efficiency, HRL-MPC exhibited the lowest energy consumption, indicating that its weight adjustment strategy effectively optimized control efficiency.

4.2.2. Tracking error curve analysis

To further analyze the transient performance of controllers in dynamic environments, Figure 4.1 shows the tracking error curves over time for the three methods in a typical experiment.

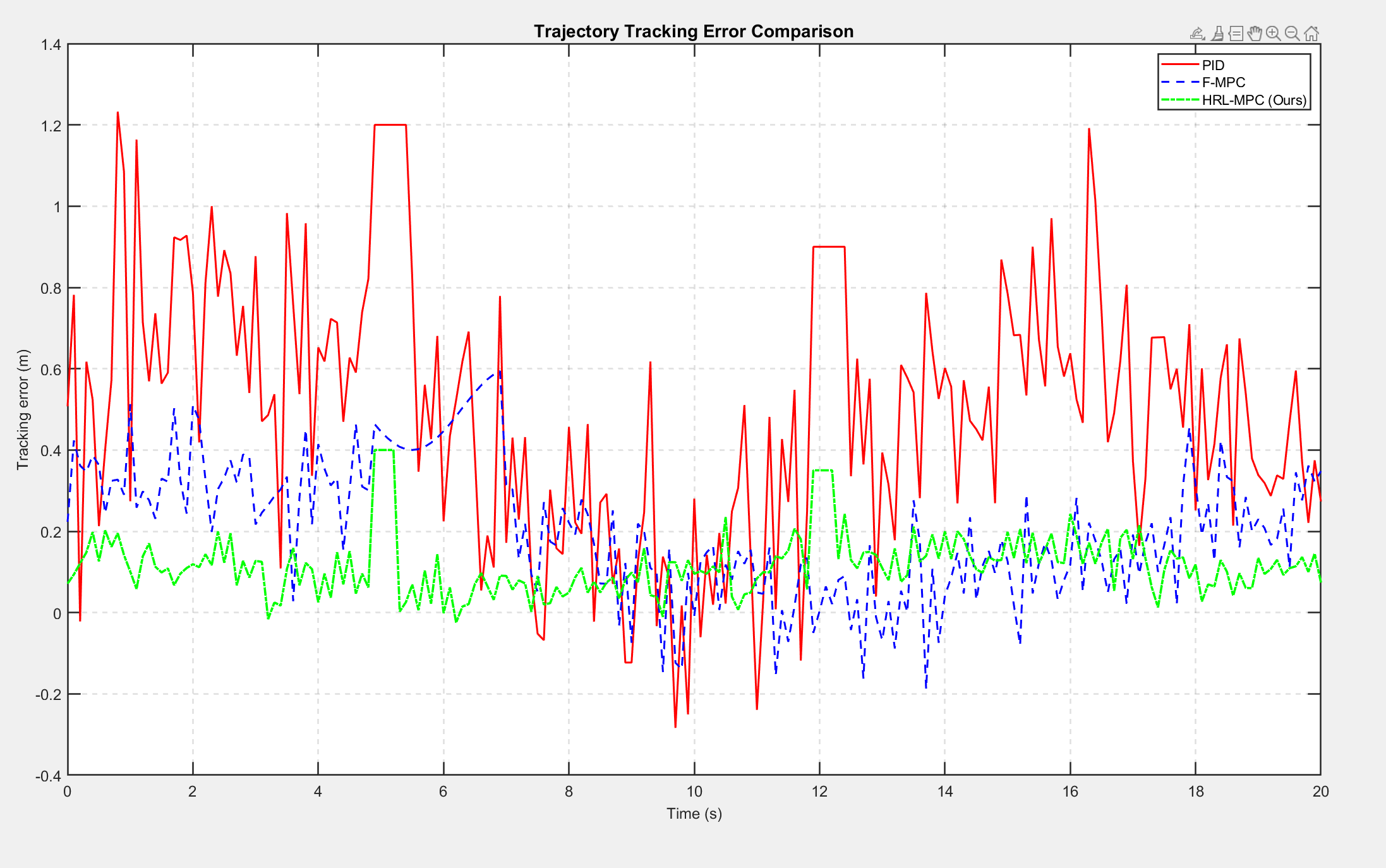
Analysis of Figure 4.1 reveals that during two dynamic disturbance events (gray shaded regions) occurring around t = 5s and t = 12s:

The error curve of the PID controller exhibits two extremely high peaks with prolonged duration, indicating collision and complete loss of tracking capability.

The F-MPC controller exhibits a significant increase in error accompanied by decaying oscillations lasting approximately 4–5 seconds, indicating its ability to avoid obstacles but with sluggish response and poor recovery to stability.

The HRL-MPC method produced only low-amplitude, extremely short-duration (approximately 0.6 seconds) spikes in error, followed by rapid convergence to a low-error range. This demonstrates that the proposed method can rapidly perceive environmental risks and minimize the impact of disturbances on tracking performance through dynamic adjustment of control strategies, exhibiting outstanding robustness and adaptability.

4.3. Summary

This chapter thoroughly validates the performance of the proposed HRL-MPC method through extensive simulation experiments. Both quantitative and qualitative results demonstrate that this method comprehensively outperforms traditional fixed-weight MPC and PID controllers in tracking accuracy, task efficiency, safety, and energy efficiency within dynamically complex warehouse environments. Its core advantage lies in real-time adaptation to environmental changes through a hierarchical reinforcement learning framework, achieving an optimal trade-off between trajectory tracking and dynamic obstacle avoidance. The experimental results strongly validate the effectiveness and advanced nature of the proposed method.

5. Conclusions

This paper addresses trajectory tracking for sorting robots in dynamic warehouse environments through a synergistic optimization study integrating hierarchical reinforcement learning (HRL) and model predictive control (MPC). Its core contribution lies in identifying and resolving the structural limitation of fixed weights in traditional MPC, proposing a novel framework where a PPO algorithm serves as the high-level meta-controller dynamically adjusting the underlying MPC weight parameters.

The main conclusions are as follows:

1.The proposed HRL-MPC framework effectively combines RL's adaptability with MPC's constrained optimization capability through a hierarchical structure, providing a robust solution for robotic control in dynamic settings.

2.Simulations show that the method outperforms both fixed-weight MPC and PID control in trajectory accuracy, task efficiency, safety, and energy consumption, demonstrating strong environmental adaptability and robustness.

3.Beyond performance gains, the framework exhibits interpretable decision-making: the agent learns to increase obstacle avoidance weight during disturbances and restore tracking weight under safe conditions. This dynamic priority allocation enhances both credibility and practical value.

In summary, this study not only validates the proposed method's effectiveness but also provides a novel, forward-looking solution for intelligent robot control in dynamically uncertain environments, demonstrating significant theoretical significance and engineering application value.