1. Introduction

In recent years, Internet of Things (IoT) devices such as sensors and tablets have been increasingly used as nodes to connect to blockchains, thanks to breakthroughs in edge computing, cloud computing and other technologies. However, these IoT devices have relatively limited storage resources. Traditional blockchain systems use a fully replicated data storage mechanism, which saves a complete copy of the blockchain ledger for each node. As the size of the blockchain increases, the storage capacity of nodes cannot bear the expense of storing the blockchain ledger, making it difficult for nodes to verify new transactions and resulting in fewer nodes in the blockchain network.

Erasure coding technology can effectively improve this situation. On the one hand, each block can be erasure-coded so that nodes with limited resources only need to store a portion of the encoding, thereby reducing the storage burden. On the other hand, through erasure coding technology, blocks can be successfully restored even when some nodes fail, ensuring the integrity of the blocks and the security of the network. Therefore, the performance of erasure coding is crucial for the storage degradation burden and recovery capability of blockchain networks.

In this paper, a detailed comparison analysis was performed on two commonly used erasure coding methods, namely (16,12) pyramid code and (15,12) RS code. The encoding process of both codes was presented, followed by the analysis of failures from a single failure to four failures. MATLAB simulations were conducted to measure the time taken by both codes when faced with different failures, using a key matrix consisting of three dimensions: storage overhead, fault tolerance, and repair cost to measure the performance of both codes. Finally, the comparison result of both codes was presented.

2. Related works

Erasure coding has been widely used in storage systems to protect against data loss resulting from hardware failures or network issues. Regenerative code (RC) and locally repairable code (LRC) are two of the most commonly used types of erasure resilient coding (ERC)-based schemes [1, 2]. RC is a type of erasure code that has been employed in various communication systems to recover lost or corrupted data packets. Examples of RC include Fountain codes [3], Raptor codes [4], Tornado codes [5], and RS codes [6]. Of these codes, RS code is the most famous and has been applied to cloud storage systems such as Amazon S3 and Google Cloud Storage [7, 8]. LRC is another type of erasure code that provides efficient and reliable data storage in distributed systems. Examples of LRC include Pyramid codes [9] and Product codes [10]. Pyramid code has been applied to various cloud storage systems such as Microsoft OneDrive and Dropbox [9].

This paper compares the performance of RS code and Pyramid code, two common erasure codes, and analyzes their strengths and weaknesses.

3. Preliminary knowledge and basic concepts

3.1. (15,12) Reed-solomon (RS) code

(15,12) Reed-Solomon (RS) code is a typical kind of Regenerating code . It achieves erasure recovery by adding 3 parity symbols to the original 12 data symbols, adding up to a total of 15 symbols. These parity symbols are calculated using mathematical formulas based on the values of the data symbols, and are used to reconstruct any missing symbols that may have been erased during transmission. The structure of (15,12) RS code can be seen in figure 1. The formulas for calculating the three parities are listed as follows:

Figure 1. The structure of (15,12) RS code.

\( \begin{cases}\begin{matrix}{p_{1k}}={d_{1k}}+{d_{2k}}+{d_{3k}}+…+{d_{12,k}} \\ {p_{2k}}={d_{1k}}+2\cdot {d_{2k}}+{2^{2}}\cdot {d_{3k}}+…+{2^{11}}\cdot {d_{12,k}} \\ {p_{3k}}={d_{1k}}+4\cdot {d_{2k}}+{4^{2}}\cdot {d_{3k}}+⋯+{4^{11}}\cdot {d_{12,k}} \\ \end{matrix}\end{cases} \) (1)

3.2. (16,12) Pyramid code

The (16,12) pyramid code is designed to correct up to four erasures, making it a more robust solution than the (15,12) RS code. It achieves this by adding four parity symbols to the original 12 data symbols, resulting in a total of 16 symbols. The parity symbols are calculated using polynomial interpolation techniques based on the values of the data symbols in each layer. The structure of (16,12) pyramid code can be seen in figure2. The formulas for calculating the three parities are listed as follows: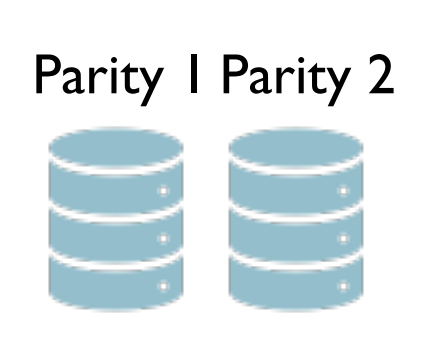

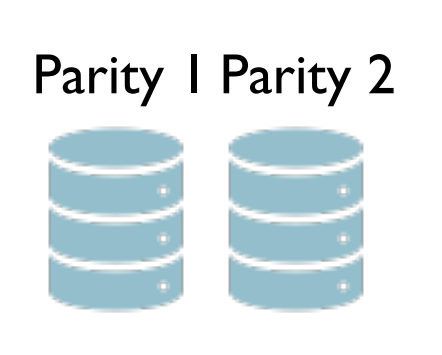
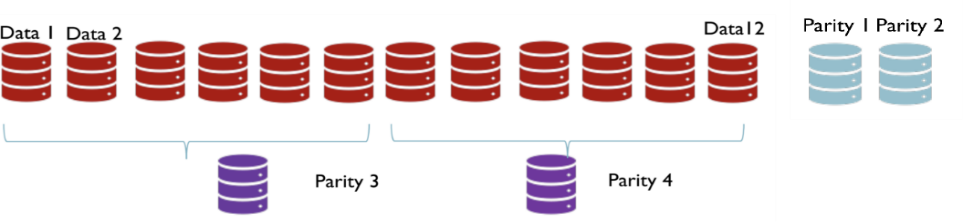
Figure 2. The structure of (16,12) pyramid code.

\( \begin{cases} \begin{array}{c} {p_{1k}}={d_{1k}}+{d_{2k}}+{d_{3k}}+...+{d_{12,k}} \\ {p_{2k}}={d_{1k}}+2∙{d_{2k}}+{2^{2}}∙{d_{3k}}+…+{2^{11}}∙{d_{12,k}} \\ \frac{{p_{3k}}={d_{1k}}+4∙{d_{2k}}+{4^{2}}∙{d_{3k}}+…+{4^{5}}∙{d_{6,k}}}{{p_{4k}}={4^{6}}∙+{4^{7}}∙{d_{2k}}+{4^{11}}∙{d_{3k}}+…+{4^{11}}∙{d_{6,k}}} \end{array} \end{cases} \) (2)

3.3. Key matrices

There are three key matrices concerning an erasure coding scheme implemented on a blockchain system.

Storage Overhead: The storage overhead is computed as the ratio between all the nodes and the data nodes, that is n/k. For the (15,12)RS code ,the storage overhead is 15/12=1.25

Fault Tolerance:. To assess the fault tolerance of an error-correcting code (ERC) scheme, a simple model proposed in [9] was utilized in this paper. This model assumes that each block, whether it contains data or redundancy information, can fail independently with a probability of p_b. When there are x failures, the recoverable ratio is denoted as \( {r_{p}}(x) \) .

\( {p_{f}}=1-\sum _{x=0}^{n}{r_{p}}(x)(\frac{n}{x}){{p_{b}}^{x}}{(1-{p_{b}})^{(n-x)}} \) （3）

Reconstruction Read Cost: Reconstruction Read Cost refers to the major cost for reconstructing data node failures, and it is defined as R(x), which represents the number of nodes required to retrieve all unavailable data nodes in the presence of x failures.

4. Encoding of blocks

To store data blocks using erasure coding, the original file blocks are first separated into k different file blocks and then encoded using (n,k) erasure coding. The file blocks are then stored on n different nodes, with k nodes containing data information and called data nodes, while the n-k nodes containing parity information are called parity nodes. During the encoding process, a generator matrix is used to achieve this step. By multiplying the information code word m by the generator matrix G, obtain the encoded code word c. The (15,12) RS code and (16,12) pyramid code have different generator matrices.

4.1. (15,12) RS code

The generator matrix for (15,12) RS code is a 12*15 matrix.

\( G=[\begin{matrix}1 & 0 & ⋯ & 0 & 1 & {2^{0}} & {4^{0}} \\ 0 & 1 & ⋯ & 0 & 1 & {2^{1}} & {4^{1}} \\ 0 & 0 & ⋱ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & ⋯ & 1 & 1 & {2^{11}} & {4^{11}} \\ \end{matrix}] \) (4)

4.2. (16,12) Pyramid code

The generator matrix for(16,12) Pyramid code is a 12*16 matrix.(

\( G=[\begin{matrix}\begin{matrix}1 & 0 & 0 & … & 0 \\ 0 & 1 & 0 & … & 0 \\ 0 & 0 & 1 & … & 0 \\ ⋮ & ⋮ & ⋮ & … & 0 \\ ⋮ & ⋮ & ⋮ & … & 0 \\ 0 & 0 & 0 & … & 0 \\ 0 & 0 & 0 & … & 1 \\ \end{matrix} & \begin{matrix}1 & {2^{0}} & {4^{0}} & 0 \\ 1 & {2^{1}} & {4^{1}} & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & {2^{5}} & {4^{5}} & 0 \\ 1 & {2^{6}} & 0 & {4^{6}} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & {2^{11}} & 0 & {4^{11}} \\ \end{matrix} \\ \end{matrix}]   \) (5)

5. Repairing of failures:

For a (n.k) .The (15,12) RS code is designed to correct up to 3 failures while the(16,12) pyramid code is designed to tolerate up to 3 failures and even some cases of 4 failures. This section analyzes the reconstruction read cost for cases of node failures ranging from a single node failure to four node failures..

5.1. Single node failure

In the case of a single node failure when encoding with (16,12) pyramid code, recovery is relatively easy since group redundancy can be used. For example, if data node 3 fails, it can be recovered by accessing parity 3 and data nodes 1-6 besides data node 3 itself, resulting in an R(1) value of 6 for (16,12) pyramid code.

On the other hand, for (15,12) RS code, global redundancy can only be used for a single data node failure. In this case, access to 12 data nodes is required to recover the erasure, resulting in an R(1) value of 12 for (15,12) RS code..

5.2. Double nodes failure

For both (15,12) RS code and (16,12) pyramid code, two equations are used to solve two unknown variables. Either of the two equations requires access to all data nodes and two parity nodes, resulting in a requirement of accessing 12 nodes to perform the recovery. Thus, the Reconstruction Read Cost R(2) for both (15,12) RS code and (16,12) pyramid code is 12.

5.3. Triple nodes failure

For both (15,12) RS code and (16,12) pyramid code, three equations are used to solve three unknown variables. Each of the three equations requires access to all data nodes and three parity nodes, so accessing 12 nodes is needed to perform the recovery. Hence, the Reconstruction Read Cost R(3) for both (15,12) RS code and (16,12) pyramid code is 12.

5.4. Four nodes failure

For (15,12) RS code, as there are only 3 parities, it can only fix up to 3 erasures. When using (16,12) pyramid code, if faced with a failure of four nodes, it can be fixed by using the four equations mentioned in part 1. However, not all of the four nodes are related to the four equations, so when all four failures occur in a single redundant group (data 1-6 + parity 3 or data 7-12 + parity 4), one of the equations may not be valid. A total of four failure cases were identified, and 2 times the number of cases could not be recovered, resulting in 3.84% of cases being unrecoverable. If the erasures are in the same redundant group, a system of linear equations would be solving four unknown variables with only three equations, making it impossible to recover the data.

6. Result and discussion

6.1. Key matrices of (15,12) RS code and (16,12)pyramid code

Table 1 shows the key matrices for (15,12) RS code and (16,12) Pyramid code that were examined in this study.

Access Efficiency. The (16,12) pyramid code is superior in its reconstruction read cost. When a single data node (say d1) fails, reconstruction read of the failed node requires six other nodes – d2, d3,d4,d5,d6 and c1. Hence, R(1) = 6, half that of the (15,12) RS code. When two or more nodes fail, both (16,12)pyramid code and (15,12) RS code takes an R(x)=12 to perform the repair.

Storage Overhead. The (16,12) pyramid code requires more storage space compared to the (15,12) RS code. The storage overhead of the (16,12) pyramid code is 16/12 = 1.33, compared to 15/12 = 1.25 of the (15,12)RS code. Hence, the improvement of access efficiency comes at the expense of increasing storage overhead. In other words, compared to the (15,12) RS code, the (16,12) pyramid code reduces reconstruction read cost by 50% with merely 6% additional storage overhead. This is a perfect example of the core concept of pyramid codes – trading storage space for access efficiency.

Fault Tolerance. To examine the fault tolerance of (16,12) pyramid code and (15,12) RS code, it can first be shown that (15,12) RS code can tolerate up to three erasures, while (16,12) pyramid code can correct some cases of four erasures, with 3.84% of cases being unable to be recovered due to statistical analysis. Assuming pb=0.01, fault tolerance can be calculated accordingly. The fault tolerance for (16,12)pyramid code is 1.02*10^-6 which is much less than 1.23*10^-5 for (15,12)RS code, indicating that (16,12) pyramid code provides a much higher fault tolerance comparing with (15,12) RS code.

6.2. Simulations of (15,12) RS code and (16,12) pyramid code

Simulations were conducted on all the cases of single node failure, double node failure, and triple node failure. There were 12 cases of single data node failure, 66 cases of double data node failures, and 110 cases of triple data node failures. Mean recovery time for each type of failure was calculated and presented in the bar chart below:

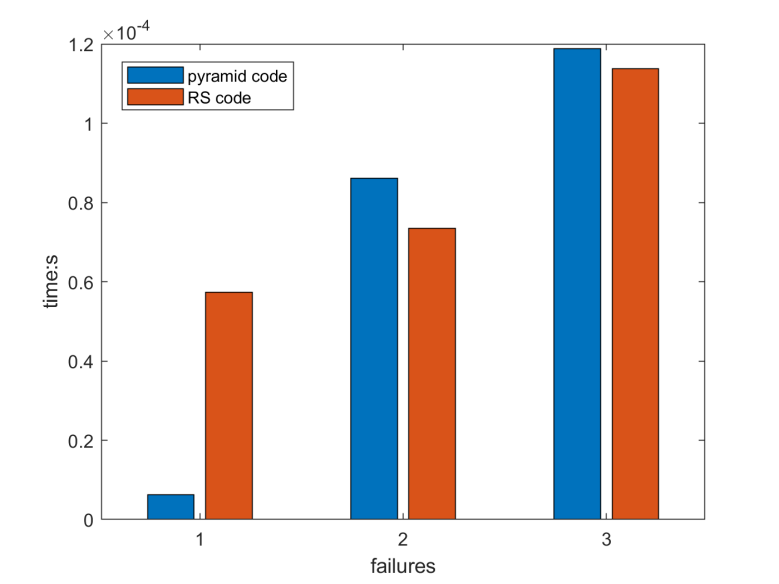
Figure 3. Bar chart for matlab simulation of repairing time of rs code and pyramid code under the cases of 1-3 failures.

As can be seen in the figure 3, the (16,12) pyramid code perform significantly better when dealing with a single node failure, spending a much smaller amount of time than that of (15,12) RS code. This is mainly due to the use of locally redundant nodes in the pyramid code (16,12). When it comes to double nodes failures and triple nodes failures, the (15,12) RS code stands out with a relatively small margin, using using a relatively smaller amount of time comparing to (16,12) pyramid code.

Based on the performance analysis conducted in this paper, it can be concluded that (16,12) pyramid code is more fault-tolerant and efficient in repair when faced with multiple node failures, while (15,12) RS code is more powerful in dealing with a single node failure but relatively less efficient in dealing with two or more node failures.

7. Conclusions

A performance analysis was conducted on two commonly used erasure coding methods in blockchain systems in this paper. The evaluation included their fault tolerance, read reconstruction cost, and storage overhead, while MATLAB simulations were used to investigate their repair capabilities in response to node failures. The results showed that (16,12) pyramid code is more fault-tolerant and efficient in repair than (15,12) RS code, even though the latter has lower storage overhead. The choice of encoding method should depend on the specific requirements of the application. Further research could explore the use of hybrid encoding schemes that combine the strengths of different methods to achieve better performance on blockchain systems. This could involve studying novel ways to intelligently select and apply different erasure codes based on specific system parameters, such as network size, storage capacity, and fault tolerance requirements. Improving the effectiveness and efficiency of erasure coding approaches could have significant implications for the security, reliability, and scalability of blockchain systems, and help to facilitate their wider adoption in various domains.