1. Introduction

In recent years, quantum computing has emerged as a promising technology that could revolutionize the field of cryptography. While quantum computers offer many potential benefits, they also pose a significant threat to traditional cryptographic schemes, which rely on challenging mathematical problems that classical computers can effectively solve. The solution to the mathematical problem led to the development of post-quantum cryptography schemes to resist attacks by classical and quantum computers. This survey aims to understand quantum digital signatures and their security potential comprehensively.

A highly promising approach in post-quantum cryptography is the utilization of quantum digital signatures. Quantum digital signatures use the tenets of quantum mechanics to derive secure digital signatures resilient to the attacks of classical and quantum computers. These signatures are all based on properties of quantum states, such as superposition and entanglement, and provide a way to verify the authenticity and integrity of digital information.

This paper's structure is as follows. The first section outlines the basic principles of quantum mechanics and cryptography, including required distribution, message signing, and verification. Section 2 discusses quantum digital signature schemes, including lattice-based, code-based, multivariate-based, LPN-based, and hash-based schemes. In the third part, this paper discusses the applications of quantum digital signatures in various fields, such as finance, blockchain, and innovative city systems. Finally, this paper summarizes the paper's main findings and discusses future research directions in quantum digital signatures.

2. Basic principles of quantum digital signature

2.1. Basic principles of quantum mechanics

2.1.1. Quantum bits (Qubits). Quantum bit is an abbreviation for a quantum bit, the basic unit of quantum information, which plays a crucial role in quantum computing. They are a quantum analogy of classical bits, but unlike classical bits, they can exist as a superposition of two possible states |0〉 and|1〉 [1].

For simplicity, the general rule is|0⟩= \( [\begin{matrix}1 \\ 0 \\ \end{matrix}] \) ,|1〉= \( [\begin{matrix}0 \\ 1 \\ \end{matrix}] \) .

These states form a standard set of orthogonal bases in quantum computing, commonly called computational bases. An arbitrary quantum state |φ⟩ can express as a linear combination of |0⟩ and |1⟩: |φ〉=α|0〉+β|1〉= \( [\begin{matrix}α \\ β \\ \end{matrix}] \) …… ①, with α and β being complex coefficients.

A quantum state |φ〉 shaped like a ① is called a quantum bit or qubit. Eq. ① demonstrates the superposition nature of the quantum state, i.e., |φ〉 is at |0〉 and|1〉 any superposition state, while a classical bit can only be 0 or 1.

Because \( {|α|^{2}}+{|β|^{2}}=1 \) , The superposition state of qubits can write as \( |φ〉={e^{iγ}}(cos\frac{θ}{2}|0〉+{e^{iφ}}sin\frac{θ}{2}|1〉 ) \) . Here, θ, φ, and γ are real numbers. Since \( {e^{iγ}} \) has no pronounced effect, this paper can ignore it. So, it can abbreviate as \( |φ〉={e^{iγ}}(cos\frac{θ}{2}|0〉+{e^{iφ}}sin\frac{θ}{2}|1〉 \) . θ and φ define a point on the unit's three-dimensional sphere. This ball calls a Bloch ball, as shown in Figure 1.

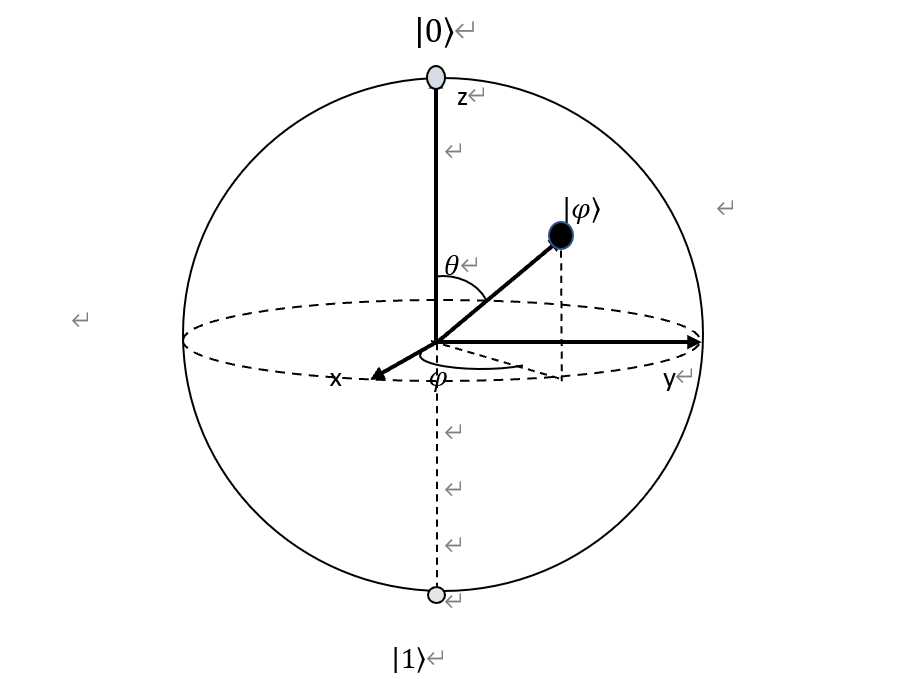
Figure 1. Bloch sphere representation of a Qubit.

2.1.2. Quantum superposition. Quantum superposition is a foundational concept of quantum mechanics, describing the ability of a quantum system to survive in multiple states simultaneously. In classic physics, an object may only be in one place simultaneously, but in the quantum world, particles can be simultaneously in multiple locations.

The concept of quantum superposition has been confirmed experimentally through numerous experiments, such as the double-slit experiment, where a beam of particles is sent through two slits and forms an interference pattern on a screen [2]. The pattern can only be explained by the particles existing in a superposition of states, with a probability distribution determined by the wave function.

In a quantum computer, quantum bits, or qubits, can survive in numerous states simultaneously, allowing for massively parallel processing. However, superposition is a fragile state easily disrupted by external factors, such as noise and environmental interactions. Thus, understanding and controlling superposition is a crucial challenge in developing practical quantum technologies.

2.1.3. Quantum entanglement. Quantum entanglement describes a phenomenon where the states of two or more quantum systems become correlated, even when separated by large distances. This phenomenon has been observed experimentally and now recognize as a fundamental property of quantum mechanics.

Einstein, Podolsky, and Rosen first introduced the concept of quantum entanglement in a 1935 paper. They argued that entanglement violates the principle of local realism, which states that physical processes should be explainable without the need for non-local influences [3]. However, many experiments have experimentally confirmed entanglement, including the famous Bell test, which proved that local hidden variables could not explain entanglement [4].

In quantum cryptography, entanglement is used to distribute cryptographic keys that are secure against eavesdropping. Attempting to intercept the keys will change the entangled state, and the parties will immediately detect the interference. In quantum computing, entanglement performs operations on multiple qubits simultaneously, enabling massively parallel processing that is impossible with classical computers [5].

Despite its potential applications, quantum entanglement remains challenging to understand and control. Its fragility makes it difficult to maintain entangled states in real-world conditions, and decoherence can quickly destroy entanglement. However, ongoing research continues to explore the possibilities and limitations of entanglement in various fields, from quantum computing to quantum metrology. It expects to play a significant role in developing future technologies.

2.2. Quantum digital signatures

2.2.1. Quantum cryptography. (1) Key distribution. Quantum key distribution (QKD) is an encryption protocol that empowers two sides to share a secret key over an unsecured transmission channel in a provably secure manner [6]. QKD, based on the laws of quantum mechanics, provides a means to detect any eavesdropper attempting to intercept or manipulate the transmitted information [6]. The securities of QKD are based on several fundamental tenants of quantum mechanics, for instance, the no-cloning theorem, the Indeterminacy Principle, and the entanglement of quantum states [6].

While practical implementations of QKD can be subject to various attacks and vulnerabilities, research has proposed techniques to mitigate them, such as decoy-state protocols, measurement-device-independent QKD, and trusted-device architectures [6]. QKD has attracted growing interest as a potential technology for secure communication in various applications, such as financial transactions, military communications, and data privacy [7].

QKD's development milestones include the first demonstration by Bennett and Brassard in 1984 [8], the introduction of the BB84 protocol by Bennett and Brassard in 1984 [9], and the first long-distance demonstration over a fiber-optic network by Hughes et al. in 2002 [10]. Numerous experimental demonstrations of QKD have been reported in the scientific literature [11].

Overall, QKD provides a strong foundation for developing future cryptographic technologies to enhance security in various applications.

(2) Using Quantum Mechanics for Message Signing and Verification. a) Eve, as the legitimate party, intercepts and manipulates the quantum gateway between the corresponding parties to perform a man-in-the-middle attack. See Figure 2.

b) During quantum key distribution (QKD), the sender transmits a quantum signal to the receiver through a quantum channel, while classical processing occurs over a classical channel using the shared information. To validate the information, Alice and Bob generate a summary using a hash function. Bob encrypts his summary using a pre-shared or private key and sends the encrypted label to Alice. Alice decrypts the label using the same key and compares it to her summary. If they coincide, authentication is successful. A two-way verification is conducted, with Bob also authenticating Alice's identity, as illustrated in Figure 2.

c) Alice and Bob exchange credentials and nonce, employing the certificate authority's public key to verify each other's public keys. They sign the message digest and non-nonce using their respective private keys to create a signature. They then use each other's confirmed public keys to verify the signatures and confirm that the messages are legally signed. Bit strings are concatenated using ∣∣∣ notation [12].

Figure 2. Schematic of a man-in-the-middle attack and flow diagram of post-quantum cryptography authentication. (From Experimental authentication of quantum key distribution with post-quantum cryptography).

2.2.2. Quantum digital signatures. Quantum digital signatures (QDS) offer a secure method for validating the authenticity and integrity of digital data by leveraging quantum mechanics principles, including quantum superposition, quantum entanglement, and the no-cloning theorem [8]. Quantum superposition allows quantum states to exist simultaneously in multiple states, while quantum entanglement links the properties of separate quantum particles, even when they are far apart. It is impossible to make an exact duplicate of an unidentified quantum state, according to the no-cloning theorem, which is a fundamental premise of quantum mechanics. This feature prevents an attacker from forging a quantum signature.

The working principle of QDS involves encoding a message into a quantum state, performing a series of quantum operations to generate a signature, and transmitting the signature along with the message over a classical communication channel. The message recipient can subsequently employ a quantum measurement to confirm the message's authenticity and integrity [7].

One advantage of using quantum signatures is their inherent security, as they rely on the laws of quantum mechanics to prevent tampering or eavesdropping by an attacker. Additionally, quantum signatures can provide a secure method for key distribution, allowing two parties to establish a shared secret key for use in encryption and other cryptographic protocols.

Challenges and limitations of quantum digital signature schemes include maintaining and transmitting quantum states and the need to develop practical and scalable quantum communication technologies. As quantum states are susceptible to their environment, preserving their coherence and preventing decoherence during transmission is a significant challenge.

2.2.3. The post-quantum digital signature. Post-quantum digital signatures are a crucial cryptography component that provides secure communication channels resistant to quantum computer attacks. With the increasing power of quantum computers, traditional signature schemes become vulnerable to attacks, and therefore, post-quantum digital signatures offer a solution for maintaining the security of digital communications. In recent years, significant research has been conducted on post-quantum digital signature schemes, including lattice-based, code-based, multivariable-based, hash-based, and LPN-based schemes. For example, in a paper published in 2021, Tang et al. proposed a new post-quantum digital signature scheme based on binary Goppa codes [13]. The proposed scheme has a minor key size and faster signing and verification than other code-based signature schemes, making it a promising candidate for resource-constrained environments. Such research on post-quantum digital signature schemes is essential for ensuring the security of digital communications in the face of the growing threat of quantum computers.

3. Types of post-quantum digital signature schemes

Table 1 compares five post-quantum digital signature schemes: lattice-based, code-based, multivariable-based, hash-based, and LPN-based. Lattice-based schemes are small in size but vulnerable to channel attacks [14][15][16]. Code-based schemes are resistant to quantum attacks but expensive and inefficient [17][18]. Multivariable-based schemes are fast and efficient but have a large key size and are prone to channel attacks [19][20]. Hash-based schemes are simple and efficient but have little information leakage risk due to hash functions [21][22]. LPN-based schemes have a minor key size but are vulnerable to quantum attacks [23][24]. Choosing a post-quantum digital signature scheme depends on specific application requirements, including security level, available resources, and acceptable trade-offs between efficiency and security.

3.1. Lattice-based

In recent years, lattice-based cryptography has gained attention as a potential solution for post-quantum digital signature schemes. A review of lattice-based cryptography and its potential for quantum digital signatures is provided in [14]. This article discusses the advantages and limitations of lattice-based schemes, including their ability to resist classical and quantum attacks but vulnerability to certain types of side-channel attacks. Another article [15] focuses on applying lattice-based cryptography in digital signature schemes, highlighting the potential advantages of smaller key sizes, faster signature generation times, and post-quantum security. However, the authors also acknowledge the limitations and vulnerabilities of these schemes. Finally, article [16] assesses the practical security of lattice-based post-quantum cryptographic schemes against side-channel and fault-injection attacks. This article emphasizes the need for careful implementation and testing to ensure the security of these schemes. Despite the challenges and limitations, lattice-based digital signatures offer a promising approach to achieving secure and efficient digital signature schemes resistant to quantum attacks.

3.2. Code-based

The article [17] presents a quantum-resistant digital signature scheme based on the Lyubashevsky framework, which incorporates principles of quantum mechanics to ensure security against quantum computer attacks. The motivation for this work is to develop post-quantum digital signatures resistant to quantum computer attacks, considering the potential threat of quantum computers to traditional digital signature schemes. The proposed scheme uses a code-based construction resistant to classical and quantum attacks, leveraging the underlying principles of quantum mechanics to achieve this level of security.

The survey of code-based digital signatures in [18] provides a comprehensive overview of these post-quantum encryption schemes that resist attacks from classical and quantum computers. While the article does not explicitly emphasize quantum digital signatures, it presents code-based digital signatures as a potential solution to the threat posed by quantum computers. The survey acknowledges some limitations of these schemes, such as their relatively large vital sizes and slow computation times compared to traditional schemes. It also highlights the most recent research and developments in the field of quantum digital signatures, providing readers with the most up-to-date information on state of the art in this area.

Overall, the proposed code-based signature scheme from the Lyubashevsky framework in [17] addresses the need for quantum-resistant digital signatures and presents a scheme resistant to classical and quantum attacks. The scheme has several advantages, including small signature and public key sizes, fast signing and verification, and resistance to classical and quantum attacks. However, it also has some limitations, such as the need for a trusted setup and the potential for some side-channel attacks.

3.3. Multivariable-based

The article [19] proposes a new digital signature scheme based on multivariate polynomial cryptography resistant to classical and quantum attacks. The scheme aims to provide post-quantum security in digital signatures, as traditional signature schemes are vulnerable to quantum computers. The article analyzes the proposed scheme's security and performance compared to other post-quantum signature schemes, highlighting its advantages, such as small vital sizes, fast signing, and verification. However, the scheme may be vulnerable to side-channel attacks. The article emphasizes the importance of developing quantum-safe digital signature schemes to prepare for the potential threat of quantum computers to traditional signature schemes.

The article [20] investigates the security of two post-quantum signature schemes, UOV and Rainbow, against fault attacks. The authors present a detailed analysis of the vulnerabilities of these schemes to fault attacks and propose countermeasures to mitigate these attacks. The article discusses the advantages and disadvantages of these schemes compared to other post-quantum signature schemes. However, the article does not explicitly focus on quantum digital signatures but rather on the vulnerability of post-quantum signature schemes to fault attacks. Nonetheless, the article provides important insights into the security of post-quantum signature schemes. It highlights the need for further research to ensure the robustness of these schemes against both classical and quantum attackers.

3.4. Hash function-based

The article [21] reports on an experimental implementation of a secure quantum network that uses digital signatures and encryption. The proposed scheme employs quantum key distribution for encryption and a hash-based digital signature scheme for authentication. The motivation for this work is to provide secure communication channels resistant to quantum computer attacks. The article describes the implementation of the network and presents a detailed analysis of its security and performance. The proposed scheme has several advantages, including resistance to classical and quantum attacks and providing secure communication channels over long distances. The plan does have some drawbacks, though, such as the requirement for specialist tools and the potential for some side-channel attacks. The paper highlights the potential of secure quantum networks in achieving secure communication channels resistant to attacks from quantum computers.

In their paper [22], Li et al. propose a one-time universal hashing quantum digital signature scheme that does not rely on perfect keys. The authors describe their method for constructing one-time universal hash functions using the Gottesman-Chuang stabilizer formalism and show how these can be used to sign messages in a quantum digital signature scheme. The motivation for this work is to develop more secure digital signatures that can resist attacks from quantum computers. The advantages of this approach include its simplicity, efficiency, and security against quantum attacks. However, the scheme has some limitations, such as a higher rate of false positives than traditional digital signatures and the need to manage secret keys carefully. Further research could focus on improving the scheme's performance and addressing these limitations to make it more suitable for practical applications.

The second article [22] proposes a one-time universal hashing quantum digital signature scheme resistant to attacks from quantum computers but also has some limitations, such as a higher rate. In contrast, the first article [21] presents an experimental implementation of a secure quantum network using digital signatures and encryption based on hash functions, which may have some limitations in terms of security and potential side-channel attacks. Therefore, further research and development are needed to improve the security and performance of quantum digital signature schemes based on hash functions.

3.5. LPN-based

Article [23] provides an overview of post-quantum cryptography (PQC), discussing its challenges and prospects for strong and secure hardware design. The authors emphasize the learning parity-with-noise (LPN) problem, which underpins numerous PQC schemes, including digital signature schemes. This paper introduces the LPN problem and its security properties and describes several LPN-based digital signature schemes, including the recent GeMSS scheme. The authors discuss the advantages and limitations of LPN-based digital signature schemes, such as their resilience to quantum attacks and relatively low computational cost. They also point out the need for careful parameter selection to ensure security. This paper provides valuable insights into the challenges and opportunities of PQC- and LPN-based digital signature schemes for robust and secure hardware designs.

The paper [24] proposes a machine-learning framework that tolerates physical noise or errors in hardware. The authors describe their approach to modeling physical noise or errors in hardware and show how it can be incorporated into the training process to improve the accuracy of machine learning models. The advantages of this approach include its ability to improve the robustness of machine learning models in the presence of physical noise or errors and its potential to reduce the need for expensive and time-consuming hardware testing. However, the scheme also has some limitations, such as the need to carefully calibrate the noise or error model and the potential for increased computational complexity. Although the paper by Kamel et al. [24] proposes a machine-learning framework that can tolerate physical noise or hardware errors, it is not directly related to LPN-based quantum digital signatures.

When comparing quantum digital signature schemes, the survey considers key size, efficiency, and security factors. To provide a more detailed comparison, specific security levels or performance benchmarks should be included as criteria, allowing for a clearer understanding of the strengths and weaknesses of each scheme. Additionally, discussing practical implementations and real-world applications of quantum digital signature schemes would offer insight into the potential use cases and practical implications of these schemes in various industries and contexts.

Future research directions in quantum digital signatures include addressing open problems and challenges related to efficiency, key size, and resistance to side-channel attacks. Furthermore, the research could focus on developing new cryptographic primitives based on quantum mechanics principles to enhance the security of digital signature schemer further.

4. Application of quantum digital signature

Table 2 summarizes several potential applications of quantum digital signatures. In the case of Bitcoin, researchers have compared classical and post-quantum digital signature algorithms to protect Bitcoin transactions. In the context of intelligent city blockchains, quantum digital signatures can help protect the blockchain while still allowing mining. Finally, quantum digital signatures can be used in the financial sector for security analysis and proposals after people have consented. These applications demonstrate the potential versatility of quantum digital signatures in various fields and highlight their importance for protecting sensitive information.

4.1. Bitcoin

Noel et al. conducted a comparison between classical and post-quantum digital signature algorithms employed in Bitcoin transactions [25]. The authors evaluate the performance of several post-quantum algorithms based on the hash function, including the XMSS, SPHINCS+, and WOTS+ schemes, and compare them to the widely used ECDSA algorithm. They show that post-quantum algorithms provide better security against quantum attacks but with increased computational complexity and larger signature sizes. León-Chávez et al. propose a hash-based digital signature scheme resistant to quantum attacks and can be implemented on current Bitcoin hardware [26]. The authors assess their scheme's performance by examining the signature size and verification time, and they compare these results with other post-quantum digital signature schemes. The proposed scheme is compatible with existing Bitcoin infrastructure and has a low computational cost. However, the scheme also has some limitations, such as its larger signature size compared to some classical schemes and the need for careful parameter selection. Both papers highlight the need for post-quantum algorithms to ensure the long-term security of the Bitcoin blockchain. These studies provide valuable insights into applying post-quantum digital signatures based on hash functions in protecting Bitcoin transactions.

4.2. Smart city blockchain

The article by Chen et al. presents a post-quantum blockchain construction for innovative city applications using quantum digital signatures [27]. The motivation behind this work is to address the security challenges of existing blockchain systems in the era of quantum computing. The authors propose a post-quantum blockchain framework that employs quantum digital signatures based on hash functions to ensure the security and privacy of innovative city applications. They evaluate the performance of their proposed framework using various innovative city scenarios and show that it outperforms existing blockchain solutions in terms of security and efficiency. The advantages of using quantum digital signatures include their resistance to quantum attacks, enhanced security and privacy, and the ability to support new cryptographic primitives. However, the authors also acknowledge some limitations, such as the need for specialized hardware and software to implement quantum digital signatures and the potential impact of future developments in quantum computing. Overall, this article provides valuable insights into the potential applications of quantum digital signatures in blockchain systems for innovative city applications.

4.3. Finance

The essay by J. Hayes [28] explains how quantum computing might be used in the financial sector. This work is motivated by the need for faster and more secure financial transactions and the limitations of classical computing in meeting these challenges. The authors emphasize the potential of quantum computing in fields like portfolio optimization, risk assessment, fraud detection, and cryptography. They discuss quantum computing methods and algorithms, such as Shor's algorithm, Grover's algorithm, and quantum annealing, which can be applied in the financial sector. The advantages of quantum computing in finance include faster and more efficient computing, better risk management, and improved security through quantum digital signatures. However, there are challenges and limitations to adopting quantum computing in finance, such as the need for dedicated hardware, the high cost of quantum computing, and the potential security risks associated with quantum cryptography. Overall, this research offers insightful information about the possible uses and restrictions of quantum computing in the financial services industry.

5. Conclusion

This investigative paper provides an overview of quantum digital signatures, a promising approach to secure and real-world digital communication in the post-quantum era. This article first describes the importance of digital signatures in modern communications and the threat of quantum computers. This article then explores the fundamental principles of quantum mechanics and quantum cryptography and how they can be used for message signing and verification. This paper then discusses the types of quantum digital signature schemes, including lattice-based, code-based, multivarious-based, and hash-based LPN-based. The advantages and limitations of each scenario are discussed. The challenges and opportunities of future research in quantum digital signatures are summarized. Future research directions in quantum digital signatures should address the open problems and challenges related to efficiency, key size, and resistance to side-channel attacks. Developing new cryptographic primitives based on quantum mechanics principles could further enhance the security of digital signature schemes. Additionally, exploring practical implementations and real-world applications of quantum digital signature schemes will offer valuable insights into their potential use cases and implications in various industries and contexts. Researchers should also investigate the integration of quantum digital signatures with other emerging technologies, such as blockchain, to leverage their potential for secure and efficient communication and transactions in the quantum era.