1. Introduction

RAID 6, or Redundant Array of Independent Disks level 6, is a disk array technology that leverages multiple disk drives to store data, providing fault tolerance and high reliability. RAID 6 is experiencing growing popularity in contemporary storage applications, particularly in sizable storage systems such as cloud storage systems. These systems often consist of many economically efficient yet less reliable disk drives, such as Serial Advanced Technology Attachments [1].

RAID 6's ability to withstand the failure of two disk drives renders it more reliable than RAID 5. Hence, RAID 6 is a common choice for applications demanding high reliability and performance, including large-scale data storage and cloud computing. Nevertheless, even with RAID 6, data corruption or loss can still occur. To mitigate this issue, RAID 6 employs error correction codes to detect and rectify data errors. An error correction code is an encoding technique that encodes raw data into redundant data, enabling the recovery of the original data in case it becomes corrupted.

Currently, RAID 6 utilizes multiple error-correcting coding techniques. Reed-Solomon code, among these, is a widely recognized error-correcting code technology that safeguards data from errors by introducing redundant information. Reed-Solomon code is esteemed for its efficiency and reliability [2]. In the context of RAID 6, Reed-Solomon code is a correction scheme, often referred to as coding (K + 2, K). Here, K denotes the number of data blocks, and K + 2 represents the total number of encoded blocks, which include K data blocks and 2 parity blocks. One of the parity blocks is created by performing XOR operations on the data block, and the other is generated using Reed-Solomon code. When data is written to the RAID 6 array, the Reed-Solomon code calculates and stores the check bits of the K data blocks and two additional parity blocks. These coding blocks hold redundant information for the original data blocks to recover data that could be lost in a disk failure event. Should a disk failure happen, RAID 6 can use the error-correcting encoding block in the Reed-Solomon code to reconstruct the missing data. The system recovers the original data by decoding and calculating the check bits, redistributing it to the other functioning disk drives [3].

2. Basic theory

2.1 Reed–Solomon error correction

During the process of data storage, the introduction of redundancy in the storage system is essential to prevent data loss when a storage node fails, thus enhancing the reliability of the node in case of failure. In classical storage systems, the more common and straightforward method of introducing redundancy is a multi-copy policy, which stores multiple copies of data. However, correction and deletion codes introduce a new strategy for adding redundancy. Compared to the multi-copy strategy, the main advantage of correction and deletion codes is that they can achieve higher reliability with the same redundancy, translating to relatively small storage costs [4].

With a given data capacity, the distance of the Maximum Distance Separable (MDS) code reaches its maximum, therefore, its fault tolerance also reaches its maximum. Moreover, the generating matrix G of MDS code possesses a property of linear independence of any column, providing significant advantages in real storage scenarios. In specific terms, when some storage nodes fail leading to the data stored therein becoming inaccessible, as long as the number of failed nodes does not exceed n-k, the data at these fault nodes can be restored through the data in any k surviving nodes [5].

Reed-Solomon code, a form of MDS code also known as RS code, is a highly popular error control code that protects data from errors by adding redundant information. Due to its simple structure, ease of implementation, and efficient decoding algorithm, Reed-Solomon code is widely used [6]. In communication systems, it can correct channel errors, improving the reliability of transmission. In storage systems, it can correct errors in disks or flash memory, preventing data loss or damage.

The encoding and decoding processes of Reed-Solomon code are founded on polynomial operations. The encoding process splits the input data into several blocks, each transformed into a polynomial. Subsequent computation of these polynomials generates error-correcting code words. The decoding process converts the received codewords back into polynomials, and through polynomial operation, detects and corrects errors. Reed-Solomon codes, compared to other error correction codes, boast efficient and swift encoding and decoding processes, coupled with potent error correction capabilities. Reed-Solomon code encodes the data to generate additional check fields that can detect and correct errors in the data. One advantage of Reed-Solomon code is that it can correct multiple errors without missing data.

2.2. Implementation analysis

Fault tolerance is a feature of a storage system that maintains the integrity of stored data when some hardware devices are disabled. In order to realize fault tolerance, many erase coding techniques are designed according to various application constraints [5]. RAID 6 (Redundant Array Independent disk) is a fault-tolerant technique commonly used in storage systems that provides additional data protection and error correction capabilities by using Red-Solomon codes. RS code in the (K + 2, K) format commonly used in RAID 6. Where K is the number of data blocks, and K + 2 is the total number of encoded blocks, including K data blocks and 2 parity blocks. This encoding method is similar to the parity algorithm used in RAID 6, but provides better reliability.

The implementation of RS codes in RAID 6 is a complex process involving encoding, decoding, performance optimization, and error recovery. In the implementation, the encoding and decoding process of RS codes is the key. During the encoding phase, the data is split into blocks and then generates redundant data for each block by some algorithm. This process requires computational power because it involves complex mathematical operations. In the RS code used for RAID 6, each data block is divided into several bytes, and each byte is treated as a symbol. Then, the operations on the Galois field are used to compute the parity block. The value of the parity blocks can be obtained by multiplying each symbol of each block by different polynomial coefficients and then adding them up. Specifically, one of the parity blocks is similar to the parity block in RAID 5 and performs XOR operations on the data block; the other parity block is generated using rs code. In RAID 6, we have two sets of parity, P1 and P2, which can be on any two disks. These two sets of parity are calculated from different independent equations; the equations must be independent so that any two elements in the equation can always be solved by other elements. To meet these requirements, we choose the van der Monte matrix from the RS code to determine the coefficients. For determining k, for 1: k, the selected system of equations isFor parity 1：P1,1 = d1,1 + d2,1 + ... + dk,1; P1,2 = d1,2 + d2,2 + ... + dk,2; ...; P1,k = d1,k + d2,k + ... + dk,k

For parity 2：P2,1 =1*d1,1 + 2*d2,1 + 22*d3,1 + ... + 2k-1*dk,1; P2,2 =1*d1,2 + 2*d2,2 + 22*d3,2 + ... + 2k-1*dk,2 ...; P2, k =1*d1,k + 2*d2,k + 22*d3,k + ... + 2k-1*dk,k. When some data blocks are missing, we can use the values of the remaining parity blocks to recover the original data. The first set of equations ensures a recovery when only one disk fails. When both disks fail, both sets of equations must be used during recovery. The application of Reed-Solomon codes in RAID 6 enables the system to tolerate multiple disk failures simultaneously and provide a high degree of data reliability and integrity. Because it allows more data blocks and parity blocks to fail at the same time without affecting data recovery, greatly reducing the risk of data loss. Therefore, the RS code in RAID 6 is a reliable storage scheme for application scenarios with high data integrity requirements.

2.3. Comparison of different error correction codes

This paper mainly introduces RS code, RDP code, liberation code and J-code, they are all the MDS array codes. In the erase code fully suitable for RAID 6, the RDP code, liberation code and J-code code all perform better than the traditional Reed-Solomon code, which requires finite domain operations during encoding and decoding. However, all the existing codes have their own advantages and disadvantages, and none of the code truly represents the factual standard of the RAID 6 code [6].

The first type of RAID-6 code is a well-known universal Reed-Solomon (RS) code that requires complex finite domain algorithms in the encoding and decoding process. Therefore, Reed-Solomon coding is expensive compared to other techniques [7].

The second type is RDP coding, which is a parity array coding technique based on the data and parity bits. Theoretical results show that the RDP-based verification disk repair algorithm can reduce the repair bandwidth, reduce the data transmission during the repair process, and shorten the repair time. Compared with the traditional repair algorithm, this algorithm can significantly reduce the bandwidth resources consumed in the inspection disk fault repair process, and improve the efficiency.

The third category is RAID-6 Liberation Code, which can be seen from the presentation [7] demonstration that Liberation code essentially has a similar geometry to RDP. Liberation The performance of the original encoding is significantly inferior to the RDP. And it can be seen that the coding complexity of RDP increases significantly with k contracting, while the curve is flat. That is why Liberation code has better scalability than RDP code. Liberation Codes are open source and have the best update performance and better scalability compared to other representative RAID-6 codes, which are widely recognized in both the academia and the storage industry.

The fourth category is J-code, which is a model for the problem of I / O imbalance and slow data recovery rate commonly used in RAID-6. J-code adopts the new check generation rule, first calculates the diagonal check-check bit constructed using the original data and constructing the new array; then calculates the position relationship between the data blocks in the new array. J-code has less encoding time compared to RDP; J-code has less decoding time and single-disk troubleshooting time compared to RDP.[8] Through theoretical analysis, J-code has low compilation and decoding complexity and single-disk fault repair I / O. The experimental results show that compared with RDP, J-code can reduce the coding time and fault repair time for single disk, while slightly under the storage utilization. In addition, the check-generation rule of J-code also alleviates the problem of disk I / O imbalance during data repair to some extent, so J-code is suitable for the underlying coding implementation of disk array, and has promising application [8].

In general, different error correction codes have their own advantages and disadvantages, and which error correction code selected mainly depends on the actual requirements and environment. For example, if you need high fault tolerance (correct multiple errors), you can choose RS code or J-code; if you require high performance, you can choose RDP code or RAID-6 liberation code.

3. Implementation process of Reed Solomon code in RAID6

3.1. Design and implementation overview

In the RAID 6, the RS code is used to protect the data, enabling it to recover the data in the case of a disk drive failure. The RS code was designed based on mathematical principles, splitting the data into blocks and generating redundant data for each block. These redundant data blocks are stored along with the original data blocks for data recovery when needed. As shown in the Figure 1.

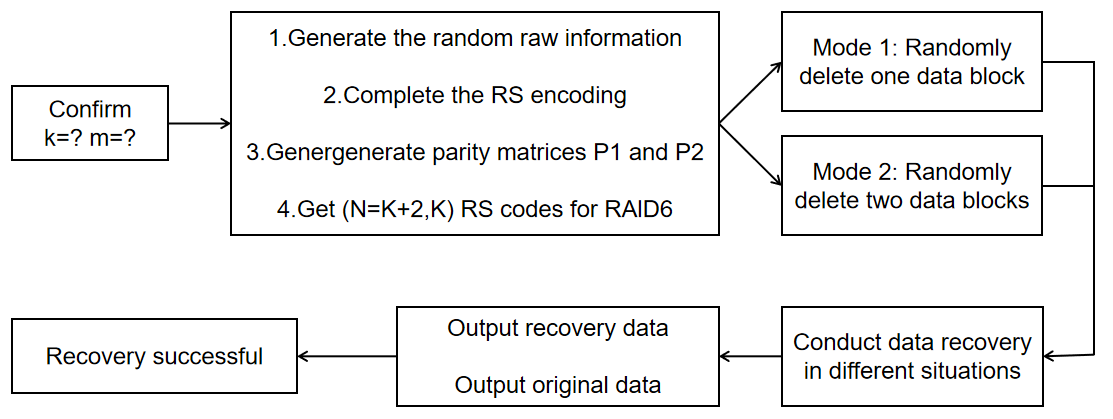
Figure 1. Utilization of Reed-Solomon Code in RAID 6 for Data Protection and Recovery (Photo/Picture credit: Original).

3.2. Complexity Analysis

From the results of the matlab code, you can get that if 1 or 2 disks are corrupted, the data can be recovered by accessing k disks. Because RAID 6 uses dual parity, it can tolerate up to two disks. The following is a specific complexity analysis:

For RAID 6 (N=K + 2, K) RS codes, there are k data disks and 2 parity disks.

When a disk is damaged, access:

One data disk is damaged: the remaining available data disk, the parity disk P1.

(2) A parity damage: the remaining available data disk.

When two disks are damaged, access:

(1) Two data disks are corrupted: the remaining available data disks, parity disks P1 and P2.

(2) Two parity disks are damaged: the remaining available data disks.

(3) A data disk and a parity disk are damaged: the remaining available data disk, the parity disk P1 and P2.

(N=K + 2, K) The RS code of RAID 6 is a common error correction encoding, whose codec complexity is linearly dependent on the size of the data block. Specifically, the encoding complexity is the O (K * N) decoding complexity of 0 (NA2), where K is the size of the data block and N is the number of data blocks. Thus, the encoding and decoding process requires longer time and larger memory for larger data blocks and higher data redundancy. It is worth noting that RS encoding with improved code-decoding complexity is suitable for small-and medium-scale data protection. Encoding technologies (such as Erasure Coding) that are more effective for large-scale data protection may be better choices.

3.3. Advantages and disadvantages analysis

The application of Reed-Solomon Code (RS code) in RAID 6 is mainly used to improve the data reliability and the fault tolerance of the system. Its main advantages include: (1) powerful error repair ability: RS codes can fix up to two disks, regardless of whether the two failed disks are in the same array. This allows RAID 6 to ensure data integrity and availability in the face of multiple disks.(2) Scalability: RS codes can be expanded as needed to accommodate disk arrays of different sizes and different performance requirements. This enables RAID 6 to be widely used in different application scenarios.

However, the application of RS code in RAID 6 also has some limitations, mainly including: (1) high computational complexity: the encoding and decoding process of RS code requires a lot of mathematical operations, which may affect the performance of the system. In particular, in large-scale disk arrays, the computational complexity of RS codes may become a bottleneck. (2) Low repair efficiency: when a disk failure occurs, the RS code needs to read all the healthy disks to perform data repair, which may lead to low repair efficiency.

Overall, the application of RS code in RAID 6 provides strong error repair ability and good scalability, but the problems of high computational complexity and low repair efficiency also need to be further addressed.

3.4. Performance evaluation

The performance evaluation of Reed-Solomon Code (RS code) in RAID 6 mainly includes the following aspects:

3.4.1. Fault tolerance. The RS code can fix up to two disks' faults, regardless of whether the two failed disks are in the same array. This allows RAID 6 to ensure data integrity and availability in the face of simultaneous failures of multiple disks. Therefore, the RS code performs well in providing fault tolerance.

3.4.2. Data recovery speed. When the disk in RAID 6 fails, the RS code needs to read all the healthy disks for data recovery. This may result to slower data recovery, especially in large-scale disk arrays. Therefore, RS codes may have some performance bottleneck in terms of data recovery speed.

3.4.3. Computational complexity. The encoding and decoding process of RS codes requires a large number of mathematical operations, which may affect the performance of the system. In particular, in large-scale disk arrays, the computational complexity of RS codes may become a bottleneck. Therefore, the computational complexity of the RS codes needs to be considered in the performance evaluation.

In conclusion, RS codes perform well in providing fault tolerance, but may have some performance bottlenecks in data recovery speed and computational complexity. In practical application, it is necessary to consider the system requirements and performance requirements and select the appropriate coding scheme. Meanwhile, other alternatives, such as RDP, RAID-6 Liberation Code, and J-Code, can be considered to meet different performance and fault tolerance requirements.

4. Advantages, disadvantages, and specific applications of alternative solutions

4.1. Row-diagonal parity

RDP code (Row-Diagonal Parity) is a binary error correction code specially designed for RAID 6. Its main application is to correct the error in RAID 6 system. It has the advantage of its low computational complexity, which makes it advantageous in scenarios with high performance requirements. However, the RDP code can only correct two errors, which limits its fault tolerance [9].

4.2. RAID-6 liberation code

RAID-6 liberation code is an improved RDP code, and its main application is also to make error correction in RAID 6 system, providing higher performance. It has the advantage of lower computational complexity and better scalability, which makes it an advantage in extremely performance-demanding scenarios. The simple structure of liberation codes, excellent performance and availability of library forms will make them popular with RAID-6 implementers. On the other hand, the disadvantages of the liberation code are also quite significant: the encoding performance is ok, and more importantly, the decoding performance is relatively poor [10].

4.3. J-code

J-code code is a new type of error correction code, which can theoretically provide higher performance and stronger error correction ability in RAID 6 applications. However, due to the new design of the J-code code, further stability and compatibility may be required in practical applications. In RAID 6, if the J-code code can be successfully applied, it will be able to provide both high performance and high fault tolerance.

5. Conclusion

The application of Reed-Solomon code in Redundant Array of Independent Disks level 6 systems is of paramount importance, effectively augmenting data reliability and bolstering system fault tolerance. Concurrently, the thorough implementation and analysis of Reed-Solomon codes play a crucial role in comprehending and optimizing the performance of RAID 6 systems. Even though Reed-Solomon codes are commonly employed in RAID 6 systems, they do pose some challenges. For instance, their high computational complexity can potentially impact system performance. Alternate approaches such as Row-Diagonal Parity, RAID-6 Liberation Code, and Johnston's Code offer certain advantages such as reduced computational complexity or superior fault tolerance. However, these alternatives also have their own constraints, necessitating a careful selection process based on specific application scenarios.

This paper delves into the use of Reed-Solomon code in RAID 6 systems, covering its fundamental theory, implementation, and analysis, as well as discussing potential alternatives. This in-depth exploration offers a robust theoretical foundation for our understanding and optimization of RAID 6 systems. Looking to the future, with the rapid growth of data centers and cloud computing, the demands for data reliability and system fault tolerance are intensifying. Consequently, further optimization of RAID 6 systems, especially selecting and implementing the most fitting coding scheme, will become a significant area of research. Simultaneously, the study and practical application of a broader range of alternatives will be critical in meeting diverse needs.