1. Introduction
Asset pricing models are crucial in financial economics, providing a framework for the behavior of asset returns under different conditions, helping investors understand and predict them. Several important models have been developed and refined over the years. The Capital Asset Pricing Model (CAPM), various Fama-French models, and the Black-Scholes model are some of the more famous models [1-3]. This introduction will discuss the historical development and current status of these models. This will help this paper in its subsequent studies on the impact of major global events such as COVID-19, regional war, and the global financial crisis on these models.
Sharpe first proposed CAMP in 1964 [1]. CAPM is among the first models to try and figure out how an asset's risk and expected return relate to each other. According to the concept, the return is determined by its sensitivity to market risk, which is shown by the beta coefficient of the asset relative to the market portfolio, as:
\( E({r_{i}})={r_{f}}+{β_{i}}(E({r_{m}})-{r_{f}}) \) (1)
Here, \( E({r_{i}}) \) is the expected return on asset i, and \( {r_{f}}, {β_{i}},E({r_{m}}) \) represent the risk-free rate, asset beta, the market portfolio's expected return, respectively. Although the CAPM has some limitations, it is still foundational and continues to be widely used in finance [1].
Black and Scholes proposed the Black-Scholes model in 1973 [2]. This model provides a framework for option pricing, which has greatly changed the pricing of derivatives. According to the model, the movement of the underlying asset’s price is a geometric Brownian motion. The formula of this model for a European call option is as follows:
\( C={S_{0}}N({d_{1}})-X{e^{-rT}}N({d_{2}}) \) (2)
where
\( {d_{1}}=\frac{ln(\frac{{S_{0}}}{X})+(r+\frac{{σ^{2}}}{2})T}{σ\sqrt[]{T}} \) , \( {d_{2}}={d_{1}}-σ\sqrt[]{T} \) (3)
Here, C represents price of the call option, S0 represents the current stock price, X is the strike price, T is the time to maturity, σ is the volatility and N is the cumulative normal distribution [2].
By including two additional factors, Fama and French expanded CAPM to obtain the three-factor model (FF3) in 1993 [3]. The FF3 model is as follows:
\( E({r_{i}})={r_{f}}+{β_{iM}}(E({r_{m}})-{r_{f}})+{β_{iSMB}}∙SMB+{β_{iHML}}∙HML \) (4)
Firm size and book to market equity were added to the new model. They are represented by SMB and HML, which means small minus big and high minus low, respectively. The difference in return between the return of a portfolio consisting of companies with small market capitalization and one with large market capitalization is known as SMB, and the difference in return between the return of a portfolio consisting of companies with higher book value and a portfolio consisting of companies with lower book value is known as HML [3]. After that, Fama and French went on to develop the model in 2015 [4]. Two factors, profitability (RMW) and investment (CMA) were added to the FF3 model. RMW means robust minus weak and CMA means conservative minus aggressive, obtaining a five-factor model (FF5):
\( E({r_{i}})={r_{f}}+{β_{iM}}(E({r_{m}})-{r_{f}})+{β_{iSMB}}∙SMB+{β_{iHML}}∙HML+{β_{iRMW}}∙RMW+{β_{iCMA}}∙CMA \) (5)
After adding these two factors, the model is more comprehensive and can explain asset returns better [4]. Recent studies have discussed the application and impact of these traditional models in some global challenges. For example, COVID-19 has caused a huge shock to the market, which has changed the basic assumptions of many asset pricing models. Zhang shows that while traditional models such as CAPM and FF3 can still provide some theoretical support, they are often not applicable to the sharp fluctuations and market dislocations caused by these crises [5]. Geopolitical risks such as regional wars also show that non-economic risk factors are important. Pastor and Veronesi show that traditional asset pricing models cannot take into account these risks, so models should be adjusted and improved to consider risks related to political instability and conflict [6].
After the world financial crisis, interest rate fluctuations made people rethink the macroeconomic variables of these models. According to Adrian, Crump and Moench, interest rate increases and monetary policy affect the risk-free rate and the overall discount rate. Therefore, models such as CAPM and FF5 need to be adjusted to make them accurate in real environments [7].
2. Financing Pricing Model under COVID-19
During the COVID-19 pandemic, several recent studies have analyzed the effectiveness of models such as CAPM and FF5 during the COVID-19 pandemic across different industries and regions. Hou and Chen used FF5 to investigate how the pandemic affected the US steel industry [8]. The study used a database to conduct a multiple regression analysis to analyze the market behavior of this industry. The data for the study were collected from the FF5 and 30 industry portfolios of steel from June 2019 to February 2020 before the pandemic and from March 2020 to September 2020 during the pandemic. To find the coefficients of the FF5 during this period, a multiple linear regression analysis was done. After this period, the sensitivity of the steel sector to fluctuations in the market decreased due to the recession in the overall economy. Before the pandemic, profitability (RMW) was an important factor, but after the pandemic, profitability became unimportant. The factors of size (SMB) and value (HML) remained important before and after the pandemic, indicating that smaller companies and those with high book-to-market ratios were influential regardless of the pandemic. The coefficient of investment style (CMA) is insignificant, indicating no substantial impact before and after the pandemic. The COVID-19 pandemic caused a recession in the US steel industry and changed the relevance of some factors in the FF5. The pandemic has changed traditional financial markets, especially profitability. Some of the results are listed in Table 1 where the bracket value gives the standard value.
Table 1: Coefficients before and after COVID-19 for steel industry [8].
Coef. Before | Coef. After | |
Mkt-Rf | 1.04(0.06) | 0.91(0.04) |
SMB | 1.15(0.12) | 0.99(0.10) |
HML | 0.46(0.12) | 0.45(0.08) |
RMW | 0.46(0.20) | 0.28(0.16) |
CMA | 0.21(0.23) | -0.08(0.22) |
The study by Kostin, Runge & Mamedova evaluated the effectiveness of FF3 and FF5 asset pricing models during crises, especially for companies in the energy industry in emerging and developed markets during this period [9]. It also questioned the effectiveness of these models during economic turmoil such as the COVID-19 pandemic. The study used data from the 12 largest global energy companies from 2000 to 2022. The Fama-French model was evaluated by calculating the equity cost for these companies and analyzing the performance of the model using the Gibbons, Ross, and Shanken (GRS) test. It was finally concluded that FF3 and FF5 models did not perform well in a crisis environment, and their results deviated from the expected results. The R2 value can show the ability to explain the changes in returns. Low R2 values indicate that these models are not suitable for predicting returns during crises, and these models cannot fully explain the changes in return data during COVID-19. They similarly conclude that the Fama-French model has limited applicability during crises like this. The factors in these models do not adequately reflect the complexity of this special period. It is suggested that models should consider the impact of crises on market dynamics to improve their reliability.
3. Financing Pricing Model under Regional War
The study by Laopodis evaluated the impact of global risks on US industry stock portfolios, considering traditional factors in FF3 and some variables of macroeconomic [10]. In particular, the study explores whether the FF model is effective in these global risks and how different industries are affected by these risks. The study used time series regression and panel data to analyze 49 US industry portfolios from 1985 to 2023. The changes in the Gulf War, the 9/11 attacks, the North Korean missile crisis, and the Ukraine-Russia war were studied to evaluate the impact of global risk factors on the model. Regional wars have different impacts on different industries and different sensitivities. Industries such as healthcare, shipping, and defense are more sensitive and positively affected, while other industries such as commercial aircraft and electronics are negatively affected. The study concluded that regional wars do have a significant impact on US industry portfolios. These risks should be considered together with traditional FF factors to fully explain and understand asset pricing.
Ediriwickrama and Azeez analyzed the impact of 20 major war-related events on IPO stock returns between 2000 and 2009 [11]. It was discovered that IPO stock returns were significantly impacted negatively by roughly 50% of war-related events. This shows that the market reacts strongly to some war events, and stock returns will decline significantly during wars. The study used multiple regression models, including SMM (the simple market model), CAPM, FF3 and C4F (the Carhart four-factor model). The study concluded that IPO stock returns were significantly impacted by Sri Lanka's civil war, and significant fluctuations were observed around key war-related events. In this study, the performance of the FF3 model was compared with simple models such as SMM and CAPM. The study found that the FF3 model had a higher R2 value than these simpler models, indicating that the inclusion of size and value helps to analyze the changes in IPO returns. But at the same time, this study also introduced the variable of war-related events, and there is a significant negative impact on IPO returns.
4. Financing Pricing Model under the Global Financial Crisis
Lim, Durand and Yang studied the relationship between factors in the FF model and the market's expected risk, especially during the world financial crisis from 2007 to 2008. The study used data of stock price from August 1st, 2005 to October 31st, 2008, and analyzed the relationship between SMB, HML, VIX (the 'fear factor'), and the market risk premium (Rm-Rf), thereby examining the impact of VIX fluctuations on these factors. The study found that the market reacted very quickly to the increase in expected risk. When VIX rises, large-cap stocks will replace small-cap companies in the eyes of investors, resulting in a decrease in size premium. And investors turn to more familiar or more liquid stocks, leading to a decline in the value premium. In the later stages of the financial crisis, the market reacted strongly to VIX fluctuations, which may be because investors had negative emotions during the crisis. Seen from Fig. 1, this resulted in an increase in the intensity and speed of the reaction, although the basic relationship between the Fama-French factors and VIX remained unchanged during the financial crisis [12].
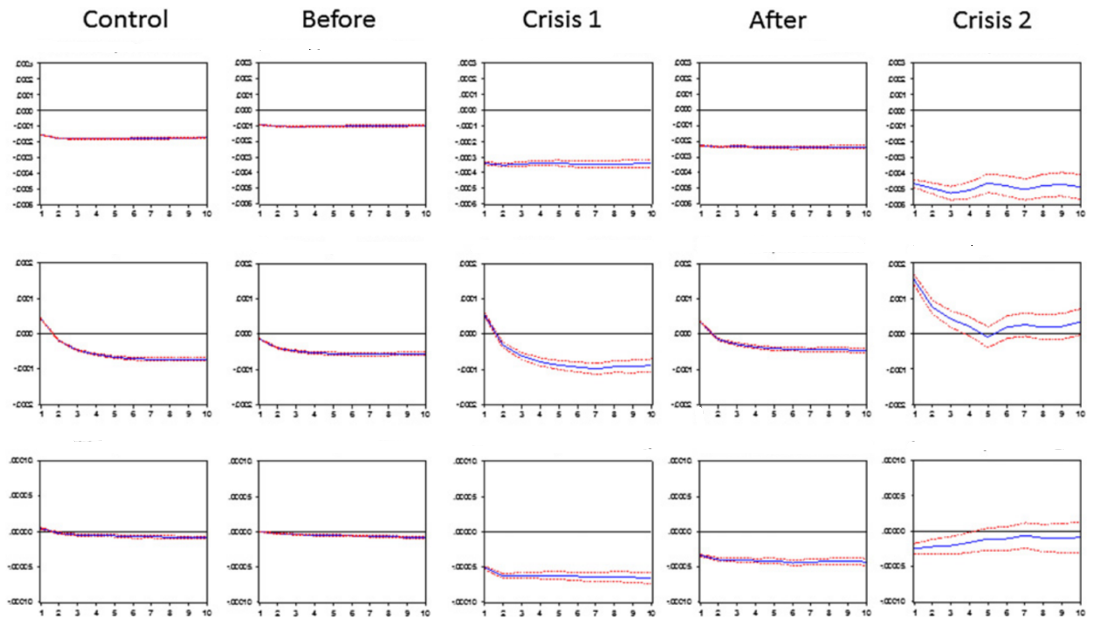
Figure 1: Cumulative impulse response functions to a shock to △VIX [12].
Yamani and Swanson studied whether the value premium in FF model is affected by financial crises. Four major financial crises were studied: the 1982 debt crisis in Latin America, the 1997 Asian financial crisis, the 1992 crisis of the European Exchange Rate Mechanism, and the terrorist attacks of September 11, 2001 [13]. It was found that the global value premium showed risk-related behavior during financial crises. The degree of integration of international financial markets increases after crises with global impacts, while it decreases after crises with regional impacts. The authors proposed a new model called GJR-GARCH-FF, which a combination of the GJR-GARCH model and the FF model, but does not include the size factor. The representation of this model is:
\( {r_{i,t}}-{r_{f,t}}={β_{0}}+{β_{MKT}}({r_{g,t}}-{r_{f,t}})+{β_{HML}}(H-L)+ \)
\( {β_{BP}}( Pound )+{β_{DM}}( Mark )+{β_{IY}}( Yen )+{ε_{i,t}} \) (6)
\( {ε_{i,t}}∣({ε_{i,t-1}},{ε_{i,t-2}},…)∼N(0,σ_{i,t}^{2}) \) (7)
\( σ_{i,t}^{2}={α_{0}}+\sum _{i=1}^{q} {α_{1}}ε_{i,t-1}^{2}+\sum _{i=1}^{p} {δ_{1}}σ_{i,t-1}^{2}+\sum _{i=1}^{r} {λ_{1}}{S_{i,t-1}}ε_{i,t-1}^{2} \) (8)
where
\( {S_{i,t-1}}=\lbrace \begin{matrix}1, & if {ε_{i,t-1}} \lt 0 \\ 0, & otherwise \\ \end{matrix}\rbrace \) (9)
The model combines value premium, market risk, time-varying risk premium and foreign exchange risk. Compared with those traditional models above, this model emphasizes the importance of considering exchange rate risk and time-varying risk premium. So, it can capture the dynamics of international returns during crises and provide a more detailed understanding [13].
5. Limitations and Prospects
According to the above and previous studies, traditional models such as FF3, FF5, CAPM, Black-Scholes, are effective most of the time, but have some limitations, especially in certain periods. CAPM is too simple because it only uses a single market risk beta to explain asset returns. This often leads to a low R-squared of CAPM, which means that it can only explain a small part of the variability in stock returns. FF3 and FF5 are extensions of CAPM. Although they are improved by adding scale, value, profitability and investment factors, some important factors are still ignored. Despite the limitations of these models, they provide a basis for further research. People can provide factors to adjust the model or expand the model to adapt to different market conditions, especially in special situations such as those mentioned above.
6. Conclusion
To sum up, this study mainly introduces the research on asset pricing models in recent years, analyzes how the predecessors used traditional asset pricing models in special periods such as COVID-19, regional wars, and financial crises, and points out some limitations of these models and how to develop. CAPM is a simple basic model that relies on a single market risk factor and often cannot explain all the variables that affect asset returns. Although the Fama-French model is more comprehensive and incorporates other factors, it still has limitations, especially in predicting returns during crises such as regional wars and COVID-19. Therefore, these models need to be further developed and improved. This will better adapt to the complexity of global financial markets. Old models can be adjusted or combined, and more factors can be added to enhance the explanatory power and predictive accuracy of these models. People should take into account the special circumstances and challenges facing the market in order to develop more powerful models and provide more reliable guidance for investment decisions.
References
[1]. Sharpe, W.F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. The journal of finance, 19(3), 425-442.
[2]. Black, F. and Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of political economy, 81(3), 637-654.
[3]. Fama, E.F. and French, K.R. (1993). Common risk factors in the returns on stocks and bonds. Journal of financial economics, 33(1), 3-56.
[4]. Fama, E.F. and French, K.R. (2015). A five-factor asset pricing model. Journal of financial economics, 116(1), 1-22.
[5]. Zhang, D. (2021). Financial market dynamics during the COVID-19 pandemic: Evidence from global asset pricing models. Journal of Financial Markets, 53, 100592.
[6]. Pástor, Ľ., and Veronesi, P. (2013). Political uncertainty and risk premia. Journal of financial Economics, 110(3), 520-545.
[7]. Adrian, T., Crump, R.K. and Moench, E. (2013). Pricing the term structure with linear regressions. Journal of Financial Economics, 110(1), 110-138.
[8]. Hou, D. and Chen, Z. (2021). Research on the application of Fama-French 5-factor model in the steel industry during COVID-19. In Journal of Physics: Conference Series (Vol. 1865, No. 4, p. 042104). IOP Publishing.
[9]. Kostin, K.B., Runge, P. and Mamedova, L. E. (2022). Validity of the Fama-French Three-and Five-Factor Models in Crisis Settings at the Example of Select Energy-Sector Companies during the COVID-19 Pandemic. Mathematics, 11(1), 49.
[10]. Laopodis, N. (2024). Fama-French Factors, Macro variables and Global Risks: Evidence from US Industry Portfolios. Macro variables and Global Risks: Evidence from US Industry Portfolios (February 03, 2024).
[11]. Ediriwickrama, T.C. and Azeez, A.A. (2016). The impact of the civil war on IPO stocks in Sri Lanka: Regression and event based analysis.
[12]. Lim, D., Durand, R.B. and Yang, J.W. (2014). The microstructure of fear, the Fama–French factors and the global financial crisis of 2007 and 2008. Global Finance Journal, 25(3), 169-180.
[13]. Yamani, E.A. and Swanson, P.E. (2014). Financial crises and the global value premium: Revisiting Fama and French. Journal of International Financial Markets, Institutions and Money, 33, 115-136.
Cite this article
Zhao,K. (2024). Financing Pricing Model under Certain Conditions: Evidence from COVID-19, Regional War and Global Financial Crisis. Advances in Economics, Management and Political Sciences,135,153-158.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Financial Technology and Business Analysis
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Sharpe, W.F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. The journal of finance, 19(3), 425-442.
[2]. Black, F. and Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of political economy, 81(3), 637-654.
[3]. Fama, E.F. and French, K.R. (1993). Common risk factors in the returns on stocks and bonds. Journal of financial economics, 33(1), 3-56.
[4]. Fama, E.F. and French, K.R. (2015). A five-factor asset pricing model. Journal of financial economics, 116(1), 1-22.
[5]. Zhang, D. (2021). Financial market dynamics during the COVID-19 pandemic: Evidence from global asset pricing models. Journal of Financial Markets, 53, 100592.
[6]. Pástor, Ľ., and Veronesi, P. (2013). Political uncertainty and risk premia. Journal of financial Economics, 110(3), 520-545.
[7]. Adrian, T., Crump, R.K. and Moench, E. (2013). Pricing the term structure with linear regressions. Journal of Financial Economics, 110(1), 110-138.
[8]. Hou, D. and Chen, Z. (2021). Research on the application of Fama-French 5-factor model in the steel industry during COVID-19. In Journal of Physics: Conference Series (Vol. 1865, No. 4, p. 042104). IOP Publishing.
[9]. Kostin, K.B., Runge, P. and Mamedova, L. E. (2022). Validity of the Fama-French Three-and Five-Factor Models in Crisis Settings at the Example of Select Energy-Sector Companies during the COVID-19 Pandemic. Mathematics, 11(1), 49.
[10]. Laopodis, N. (2024). Fama-French Factors, Macro variables and Global Risks: Evidence from US Industry Portfolios. Macro variables and Global Risks: Evidence from US Industry Portfolios (February 03, 2024).
[11]. Ediriwickrama, T.C. and Azeez, A.A. (2016). The impact of the civil war on IPO stocks in Sri Lanka: Regression and event based analysis.
[12]. Lim, D., Durand, R.B. and Yang, J.W. (2014). The microstructure of fear, the Fama–French factors and the global financial crisis of 2007 and 2008. Global Finance Journal, 25(3), 169-180.
[13]. Yamani, E.A. and Swanson, P.E. (2014). Financial crises and the global value premium: Revisiting Fama and French. Journal of International Financial Markets, Institutions and Money, 33, 115-136.









