1. Introduction

Against the backdrop of global economic integration and digital transformation, the financial services industry is undergoing unprecedented changes. As an important part of property insurance business, auto insurance plays a pivotal role in this change [1]. As a risk management tool, auto insurance helps society achieve financial stability by transferring and dispersing risks, and provides individuals and businesses with economic protection in multiple dimensions [2]. However, with the surge in global car ownership and the awakening of consumers' insurance awareness, competition in the insurance market has become increasingly fierce, and the game pattern in the market has become more diverse and dynamic. In such a market environment, insurance companies are no longer a single game subject. They form an intricate game network together with consumers, regulators, reinsurance companies and other financial service providers. In order to stand out from the competition, insurance companies often adopt various strategies, such as price wars, product innovation, and service improvement. These strategies have promoted the progress of the industry to a certain extent, but have also brought some problems, such as profit decline caused by price wars and adverse selection caused by information asymmetry [3,4]. These problems not only affect the operating efficiency of insurance companies, but also pose a threat to the sustainable development of the entire industry. In this context, in-depth research on the game behavior between insurance companies and its impact on the industry is of great practical significance. This can not only help us gain insight into the internal operating mechanism of the insurance market, accurately grasp the difficulties and opportunities encountered by insurance companies in competition, and thus tailor a more competitive strategy for them; it can also provide decision-making references for regulatory agencies, help them formulate more scientific and reasonable regulatory policies, and guide the market towards fair competition and healthy development; at the same time, it can also make consumers more clear about the connotation of insurance products and services and make more wise insurance choices. In existing research, the exploration of auto insurance pricing is mostly focused on statistical modeling and quantitative analysis, or focuses on the application of artificial intelligence in commercial auto insurance, while research on qualitative analysis from the perspective of game theory is relatively scarce. This research fills this gap by introducing game theory as a powerful tool to deeply explore how the three different types of games—cooperative and non-cooperative games, games with complete and incomplete information, and static and dynamic games—shape the behavior patterns of insurance companies and consumers under market mechanisms. By constructing a payoff matrix, this paper will simulate the strategy choices and payoffs of each party in different game scenarios and provide game strategy optimization.

2. Theoretical Basis of Auto Insurance Product Pricing

Auto insurance is a financial product designed to protect car owners from losses caused by accidents, theft, or damage. Car owners pay premiums in exchange for this protection, which transfers the risk of specific potential financial losses from individuals to insurance companies [5]. Based on the coverage and liability division, auto insurance products are mainly divided into compulsory traffic insurance (motor vehicle traffic accident liability compulsory insurance) and commercial insurance [6]. Liability insurance occupies a core position in auto insurance. In many countries and regions, the law requires car owners to purchase liability insurance within a certain limit. Commercial insurance is insurance that car owners can voluntarily purchase according to their needs, including vehicle loss insurance, third-party liability insurance, theft insurance, glass breakage insurance, spontaneous combustion loss insurance, and no-deductible special insurance [7]. The business process of commercial auto insurance covers the entire journey from policy purchase to claims processing, which can be roughly divided into three stages. The business process begins at the underwriting stage, where customers choose the appropriate insurance product; claims processing is a key component of commercial auto insurance, involving damage assessment, claim submission, and compensation payment after the accident; risk management is another crucial aspect of commercial auto insurance operations, which aims to reduce the risk exposure of insurance companies and enhance operational safety [6]. Among them, auto insurance product pricing is the process by which insurance companies determine premiums based on a variety of factors, mainly considering the following factors: vehicle type and value, driver age and driving experience, driving record, vehicle usage nature, regional differences, and insurance history [7]. Auto insurance product pricing not only reflects the risk management capabilities of insurance companies but also reflects their market competitiveness and customer service awareness. A reasonable pricing strategy can not only ensure the profitability of the company but also provide customers with fair and attractive protection plans. Therefore, scientific auto insurance pricing is the key to achieving a win-win situation for insurance companies and consumers.

3. Basic Concepts and Model Characteristics of Game Theory

Game theory is a mathematical model that studies the interaction between decision-makers. It is used to analyze how each participant maximizes their benefits by choosing strategies under specific rules. It is applied in fields such as economics, political science, and sociology to understand and predict behaviors and outcomes in various competitive or cooperative situations. Understanding some key terms in game theory is very important for subsequent discussions. Participants are individuals or decision-making units that make decisions in the game. Each participant chooses a strategy based on his or her understanding of the rules of the game and his or her expectations of the behavior of other participants and usually seeks to maximize his or her interests or utility through the optimal strategy. The interaction between participants determines the outcome of the game. A strategy is a complete plan of action, which specifies an action at every node assigned to a player. In the game of considering vehicle insurance, the 'participants' can be insurance companies and consumers, while the 'strategies' may include price setting, insurance selection, etc. The benefits are the rewards or results obtained by the participants based on their strategy choices and are usually used to measure the success of their decisions. Nash equilibrium is an important concept in game theory, used to describe a situation. Let G=(N,A,u) be a game, where N is the set of participants, A=A1×A2×...×An is the set of action combinations, and u=(u1,u2,...,un) is the utility function. The strategy combination a*=(a1*,a2*,...,an*) is called a Nash equilibrium if for all i∈N and all ai∈Ai: ui(a_i*,a_-i*)≥ui(ai,a_-i*). That is, each participant's strategy is the best response to the strategies of other players, and no player has the motivation to change the strategy unilaterally.

First, as a representative of non-cooperative games, the prisoner's dilemma reveals that individual rational behavior may lead to the damage of collective interests. In insurance pricing, the prisoner's dilemma can be used to analyze the dilemma of insurance companies in price competition. If each company reduces premiums to maximize its own interests, it may eventually lead to a decline in profits for the entire industry. But if insurance companies can use some strategies to avoid price wars, such as introducing evolutionary dynamics models to simulate the behavioral trends of participants after multiple interactions, or introducing incentive mechanisms to allow negotiation and communication, they can achieve better collective interests [7]. Second, in the context of information asymmetry, the signaling game model provides us with a window to understand the interaction between participants and alleviate the problem of information asymmetry. It is an important tool for analyzing information asymmetry and strategy transmission. Participants influence the decisions of others by sending signals. The transmission of information is usually carried out through prices, behaviors or other observable signals. The receivers adjust their decisions based on these signals. Finally, from the perspective of dynamic games, the sequential game model reveals the timing factors that insurance companies need to consider when pricing. This model focuses on the situation where participants make decisions in sequence. The strategy of each participant not only affects its own benefits, but also has an impact on other participants. In this process, insurance companies that act first can formulate pricing strategies based on their own advantages to seize market opportunities; while companies that act later need to observe the pricing of competitors and flexibly adjust strategies based on their own circumstances to find a suitable position in the competition. This dynamic strategic interaction makes insurance pricing more flexible and adaptable.

4. The Application of Game Theory in the Pricing of Auto Insurance Products

The complexity and dynamism of the auto insurance market make the interaction between insurance companies and consumers full of strategies and uncertainties. Game theory, as a powerful analytical tool, can reveal the logic behind these interactions and provide theoretical support for optimizing the auto insurance pricing mechanism. This paper will explore the game phenomenon in auto insurance pricing from two main aspects: the game between insurance companies (4.1) and the game between insurance companies and consumers (4.2). In each part, this study will conduct an in-depth analysis from the perspectives of three important game categories. The first one is cooperative and non-cooperative games, it explores whether there is a formal or informal cooperation mechanism between participants. The second one is complete information and incomplete information games, it analyzes the impact of information transparency in the market on the decision-making of all parties. The last one is static and dynamic games, it considers the role of time factors in the decision-making process. The systematic analysis of the above three perspectives reveals the complex game phenomenon in auto insurance pricing and can also provide theoretical basis and practical guidance for formulating more scientific and reasonable pricing policies.

4.1. Game Between Insurance Companies

4.1.1. Cooperative and Non-cooperative Games

In the auto insurance market, competition between insurance companies often takes the form of price wars. When two or more companies offer similar products at the same time, each company faces the decision of whether to lower prices to attract more customers. Suppose the two parties in the game are: Insurance Company A and Insurance Company B. Both Insurance Company A and Insurance Company B have two strategies: maintaining high prices and lowering prices. Under certain ideal market conditions, this scenario can be described by the following traditional prisoner's dilemma, but remember that the actual auto insurance market is often more complex and changeable.

Table 1: Profit matrix

Explanation: In this payoff matrix, the numbers in each cell represent the returns (profits) of the two companies under different strategy combinations. The first number in the brackets is the return of Company A, and the second number is the return of Company B. The values in this payoff matrix are hypothetical data, which are intended to illustrate the relative returns under different strategy combinations, rather than reflecting specific profit figures in the actual market. Through this hypothetical model, can demonstrate the core problem of the prisoner's dilemma, as shown in table 1.

Analyze: (8, 8): If both companies maintain high prices, they may lose some price-sensitive customers, but overall industry profits will be higher because they are not caught in a price war. (10, 2)If Company A lowers its prices and Company B maintains high prices, the opposite will happen: Company A will gain more customers while Company B will lose market share.

(2, 10): On the contrary, if Company A maintains high prices and Company B lowers its prices, Company B will attract more customers and thus gain a higher market share, while Company A will lose some customers.

(5, 5): If both companies choose to lower prices, although they may attract more customers in the short term, due to the cost structure, it will eventually lead to a decline in overall industry profits and the long-term benefits of both parties will be damaged.

For insurance company A, no matter what strategy insurance company B adopts, since eight is less than ten and two is less than five, the best response of player A is always to reduce the price, so price reduction is the dominant strategy of insurance company A, and the same is true for insurance company B. As a result, all participants will choose their dominant strategy to act, and (L, L) (that is, both companies choose to reduce the price) is a Nash equilibrium point. This means that in this state, unilaterally changing the strategy of either party will not increase its benefits, so both don't have the motivation to change minds unilaterally and only want to persist in their choices.

Through the analysis of the payment matrix, it can be seen that in the pricing game between insurance companies, the potential for pricing coordination depends on whether a mechanism for cooperation can be found. Although (H, H) (i.e. both companies maintain high prices) is more beneficial to both parties, in the absence of a trust mechanism or cooperation agreement, both parties tend to fall into the suboptimal state of (L, L). Finding opportunities for cooperation in the fierce market competition and avoid falling into the prisoner's dilemma has become a problem that insurance companies must face. If both parties can reach cooperation under a constraint mechanism that encourages cooperation between the two parties, they will both get more generous benefits and avoid price wars [8]. This situation is like a cooperative game.

4.1.2. Games of Complete and Incomplete Information

In the auto insurance market, insurance companies play games with complete information and incomplete information. The complete information game has several main characteristics: high transparency, strong predictability, strong stability, and easy identification of Nash equilibrium [9]. If all participants (i.e., insurance companies) can accurately know the cost structure, market strategy, and future action plan of other companies, then the insurance company can make the best response based on the other party's strategy, that is, predict the other party's response and choose the best strategy through payoff matrix analysis. This is an ideal situation. Due to the characteristics of the complete information game, insurance companies can coordinate their behaviors more effectively, reduce inefficient competition, and develop the industry healthily. When all participants have a high degree of understanding of each other's cost structure, companies will carefully weigh the relationship between their own and the other party's costs and potential benefits, calculate the results of various strategy combinations in advance, and accurately predict the behavior of their opponents. Any attempt to squeeze out competitors through low-price dumping will be immediately detected, avoiding aggressive price wars to a certain extent.

In contrast, in an incomplete information game, insurance companies cannot fully grasp all information about their competitors, and competitors may also conceal some key information. For example, an insurance company may not be able to accurately understand the risk control capabilities and cost structure of another company, which will lead to greater uncertainty for insurance companies when formulating pricing strategies. In order to cope with this uncertainty, insurance companies need to adopt some strategies to compensate for the impact of information asymmetry. For example, insurance companies can collect information about competitors through market research, data analysis, and other means.

It can be seen from this that in a complete information game, insurance companies can take advantage of their high transparency, strengthen cooperation with competitors, and jointly formulate industry standards and pricing rules. This can not only improve the accuracy and rationality of pricing, but also reduce unnecessary competition and promote the stable development of the market. In an incomplete information game, insurance companies need to adopt more flexible and cautious pricing strategies. They can use big data analysis technology to strengthen monitoring and research on competitors, and collect and analyze competitors' market dynamics and pricing changes in real time [10].In addition, insurance companies can enhance their competitiveness by strengthening brand building and improving service quality.

4.1.3. Static Game and Dynamic Game

The key feature of static games is "instant decision-making" and no participant can make adjustments based on future actions. Since participants make decisions at the same time, the core of the game is how to predict the actions of the other party at the same time and achieve Nash equilibrium through a combination of strategies. In the n-person game in the auto insurance market, each company can choose two strategies: low premium or high premium. Each insurance company will adjust its own strategy according to the pricing strategy chosen by other companies to ensure that no company can gain more market share or higher profits by unilaterally changing its strategy. This analysis helps insurance companies make rational decisions in fierce competition, avoid excessive price wars, and promote market stability. In static games, all insurance companies make decisions at the same time, which means that they need to reach a stable state at the same time. Risk-diversified pricing strategies can help insurance companies achieve a balance between risk and return at this point in time, alleviate the financial pressure caused by concentrated compensation for a certain risk group, and avoid market fluctuations caused by unilateral aggressive strategies [11].

Dynamic game analysis reveals the impact of time factors and sequential behavior on market dynamics. By extending formal analysis, can more accurately evaluate the expected returns under different strategy combinations and provide theoretical support for practical decision-making.

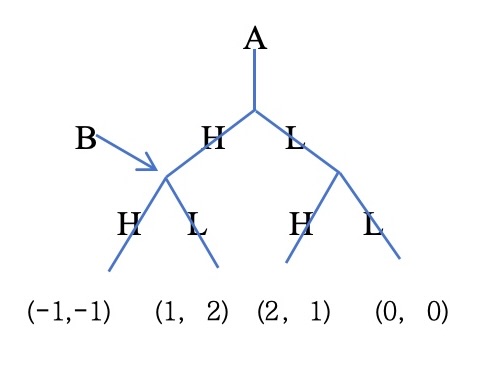
Figure 1: Extensive form

Table 2: Normal form

Explanation: Because insurance company B needs to specify a response for each choice of A (high premium or low premium), the strategy of company B can be seen as a combination of two choices. 'HH ' means if company A chooses high price (H), company B will choose high price (H), if company A chooses low price (L), company B will choose high price (H), as shown in figure 1.

Analysis: Company A needs to predict the reaction of Company B and decide whether to lower the price (choose H or L) first. Company B decides whether to lower the price (choose H or L) after observing the choice of Company A. Company B will make the best response according to the choice of A. From the payoff matrix, can see that there are three equilibriums, but it seems to be strange when Company A chooses the high price strategy H and Company B chooses the LL strategy. Insurance Company A chooses first, so it is not logical for it to choose the high price. (1,2) is best for Company B, so Company B will 'tell' Company A that it will choose low price no matter what Company A chooses, as shown in table 2. However, Insurance Company A will ignore B's words because A knows if it choose low price, Company B will follow to choose a high price because 1>0. As a result, Insurance Company A will choose the low price and Insurance Company B will choose the high price. So from this game, can see that price war seems to be an incredible threat. So in an ideal situation, through the analysis of sequential games, it can be considered that price wars are unlikely to occur or will not last for a long time. Insurance companies will choose more stable and sustainable pricing strategies based on rational decision-making and long-term interests, and enhance their lasting competitiveness through non-price competition means, such as improving service quality, innovating insurance products, and strengthening brand building.

4.2. Game Between Insurance Companies and Consumers

4.2.1. Cooperative and Non-cooperative Games

Insurance companies hope to encourage consumers to share more information about driving behavior and risks by providing incentives (such as discounts), to more accurately assess risks and formulate more reasonable pricing strategies. This is a cooperative game. By designing incentives, insurance companies and consumers establish a relationship based on common interests, mutual trust, and long-term cooperation. This interaction is not just a unilateral decision, but the result of joint efforts of both parties. For example, consumers can get premium discounts by installing dashcams and sharing data, and insurance companies can also more accurately assess the driving risks of each consumer.

Some consumers may choose to conceal bad driving records (such as accidents or violations) to obtain lower premiums, increasing the risk to insurance companies. Both participants choose strategies that maximize their benefits out of selfish motives.

Table 3: Profit matrix

Analyze: (5, -3): Consumers get higher discounts and convenience by truthfully declaring and sharing data. Insurance companies bear certain risks but can attract more consumers.

-6): Consumers avoid potential high premiums by concealing information, but insurance companies face greater risks. Insurance companies fail to detect high-risk behaviors due to lax audits and ultimately bear greater compensation risks.

(3, -1): Consumers get a modest discount and reduce some compliance costs. Insurance companies reduce risks through strict audits, but this may affect consumer satisfaction.

(-1, 0): Concealing information is unlikely to work, and consumers face fines or higher premiums, while strict review ensures the authenticity of information and reduces the risk of claims.

In a non-cooperative game, insurance companies need to establish a strict audit mechanism to deal with consumers who conceal bad driving records. Consumers declare truthfully and insurance companies conduct strict audits ((3,−1)) is the final Nash equilibrium point, but it is not the most ideal situation, as shown in table 3. This is because strict audits increase consumers' compliance costs, reduce satisfaction, and may lead to customer churn, affecting market share and brand reputation. At the same time, in a highly competitive market, other insurance companies may attract consumers through more relaxed audits or higher discounts, weakening the competitiveness of strict audits. Therefore, insurance companies may need some improved incentive mechanisms to achieve better market equilibrium and a win-win situation.

4.2.2. Games of Complete and Incomplete Information

Consumers convey information to insurance companies by choosing different insurance products. For example, choosing a product with a high insurance amount may mean that the consumer considers themselves a high-risk customer (R), while choosing a product with a low insurance amount may indicate that they are a low-risk customer (S).

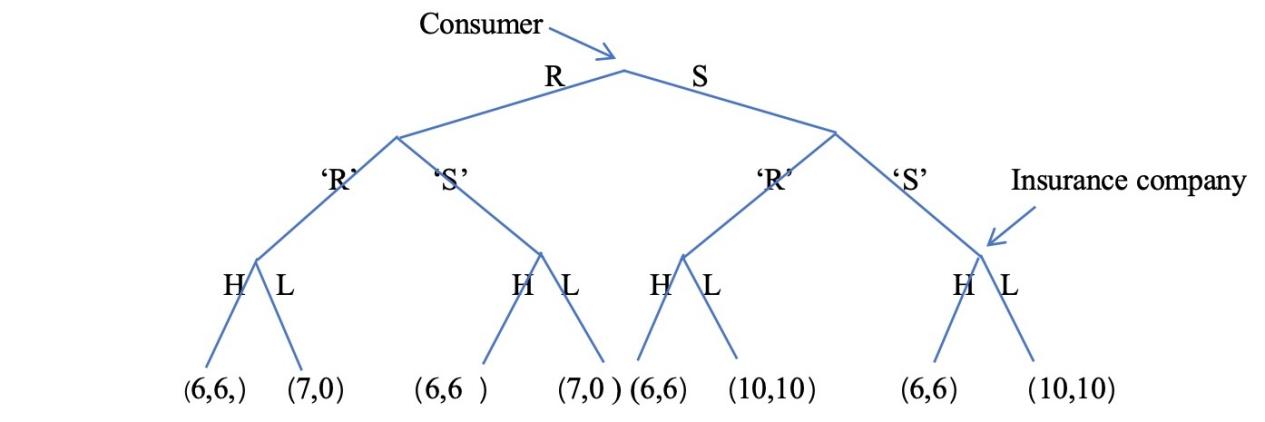
Figure 2: Signal game

Analyze: Consumers choose whether to send signal 'R' or 'S', and insurance companies will adjust their pricing strategies (H or L) according to the signals sent by consumers. Both R and S want to send the same signal'S'. It is a pooling equilibrium because, in this situation, all types of players choose the same strategy and send the same strategy, making it impossible for the receiver to distinguish between different types based on the observed actions. This is not a good thing for insurance companies. They can increase the cost of sending signals (S) through verification mechanisms or introduce some penalty mechanisms, as show in figure 2.

When there is information asymmetry between the two parties in a transaction, high-risk customers may be more inclined to purchase insurance, while low-risk customers may choose not to purchase insurance or choose products with lower insurance coverage. This leads to adverse selection, which means that when there is information asymmetry between the two parties in a transaction, the party with more information uses this information advantage to make a choice that is beneficial to itself but disadvantageous to the other party, resulting in reduced market efficiency [12].

4.2.3. Static Game and Dynamic Game

At a certain moment, insurance companies and consumers make decisions at the same time. Consumers decide whether to purchase insurance and which product to choose, while insurance companies decide whether to accept insurance and pricing strategies. Market participants make optimal decisions under specific constraints, and government regulators formulate more effective regulations based on the results of static game research to promote the healthy development of the market. Over time, consumers' claims behavior will affect the future pricing strategies of insurance companies. Assume that consumers' claims behavior after purchasing insurance is divided into two categories: low-frequency claims and high-frequency claims. For low-frequency claims, insurance companies may maintain or reduce premiums (to encourage customers to continue to purchase insurance and maintain a good relationship. For high-frequency claims, insurance companies are more inclined to increase premiums or refuse to renew to reduce future payment risks. This dynamic game helps insurance companies develop more flexible and adaptive strategies, while also providing consumers with a clear behavioral incentive framework.

4.2.4. Auto Insurance Pricing Strategy Optimization Suggestions

This article focuses on the application of game theory in auto insurance pricing and analyzes the game phenomenon between insurance companies and consumers. In response to the prisoner's dilemma of price wars between insurance companies, it is recommended to establish an industry pricing coordination mechanism, organize regular consultations through industry associations, formulate guiding pricing standards, guide reasonable pricing, avoid vicious competition, and achieve win-win cooperation. Under the complete information game, insurance companies should strengthen information collection and analysis, use advanced technology to monitor market dynamics in real time, optimize risk assessment models, accurately price, and maintain market stability.

In the face of cooperative games with consumers, insurance companies need to optimize incentives. In addition to premium discounts, they should provide customized value-added services, differentiate incentives according to consumer driving behavior and risk levels, and promote information sharing. In non-cooperative games, third-party risk assessment agencies are introduced to independently and objectively assess consumer risks, reduce audit costs and consumer dissatisfaction. For personalized pricing in complete information games, deep digging into consumer multi-dimensional data, accurately formulating personalized plans; and under incomplete information games, improve risk identification mechanisms, integrate multi-source data to distinguish high-risk and low-risk customers, differentiate pricing, and reduce adverse selection.

From the instant decision-making of static games to the long-term impact of dynamic games, insurance companies should implement dynamic pricing based on driving behavior, collect data in real time to adjust premiums, encourage safe driving, make pricing close to actual risks, and achieve a transition from static to dynamic. These strategies help insurance companies to set prices scientifically in competition and achieve win-win and sustainable development for all parties.

5. Conclusion

In addition to cooperative games, non-cooperative games, complete information games, incomplete information games, static games and dynamic games discussed in this paper, future research can introduce more game types such as evolutionary games and random games to deeply analyze the evolution of pricing strategies and market equilibrium states in the auto insurance market under different game environments. For example, evolutionary games can simulate the dynamic evolution process of strategies in the insurance market and reveal the dynamic equilibrium mechanism of long-term competition and cooperation. Based on the current research results, further exploration can be carried out from the perspective of technology-driven innovation in the future. Although this study has put forward many valuable insights, there are still some limitations that need to be improved. Data acquisition is restricted by commercial confidentiality and personal privacy, which affects the depth of empirical analysis; simplified model assumptions may not fully reflect the complexity of the real world; regional differences are not considered enough, and the impact of factors such as the legal environment and cultural background of different countries and regions on game strategies has not been fully discussed; long-term effect evaluation is missing. Current research focuses more on short-term behavior patterns and lacks long-term impact evaluation such as market structure evolution and changes in consumer behavior habits. In summary, this paper provides valuable theoretical guidance and practical suggestions for insurance companies through the analysis of pricing game strategies for auto insurance products, but it still needs to be explored and improved in the future to cope with increasingly complex market challenges.