1. Introduction

Mortgage-backed security is a type of asset-backed security which is secured by a mortgage or collection of mortgages. Residential mortgage-backed securities (RMBS) and Commercial mortgage-backed securities (CMBS) are two main types of MBS. RMBs are debt-based assets backed by the interest paid on residential loans, and CMBs are debt-based assets backed by the interest paid on commercial loans. Although MBS are backed by either government agency or financial institution, the actual cash flow depends on the payment made by the mortgagors. Thus, there are two types of risk that can harmfully affect the value of the loan, Prepayment and default risk. When the borrower decides to pay off the loan early, and the loan terminates before its expected ending date, this is called prepayment. When the borrower decides to stop making payments on the mortgage, this is referred to as a default. The residential mortgage default/prepay usually happens when the buyer is in a financial problem to afford the mortgage, the drop of interest rate, or move to the other place. Commercial mortgage default/prepay usually occurs when the real estate business is not profitable anymore or the economy worsens so the owners are not able to collect the rent. This paper studies the loss from credit events in the mortgage markets. It identifies a proper way to estimate credit loss and studies how credit losses are transferred through MBS products, including Commercial Property Mortgage products (CMBS) and residential property mortgage products (RMBS). A credit loss model is built from a top-bottom approach, starting from national/regional level economic and real estate market conditions and then refining to individual mortgage losses.

2. Literature review

Previous research had analyzed some macro-economic factors that affect the prepay or default of MBS. Mikhail Chernov, Brett R. Dunn, and Francis A. Longstaff [1] analyzed the compiled table of implied spread liquidity, rate response, and turnover rates that are different than those of actuals (fixed time scope, same securities), which means MBS have significant prepayment risk premiums. Besides that, research data also showed that macroeconomic factors are also important by driving the prepayment risk. Another research mainly focused on examining the relationship between the yield curve and prepayment or default [2]. By applying different variables to the model, the results showed that a one-point increase in the yield curve results in 70% decrease in the odds of prepayment and a 49% decrease in the odds of default, which proves that an increase in yield curve slope will effectively decrease the chance of mortgage termination. Several research have been conducted to analyze how macro-economic factors influence Adjustable-Rate Mortgage (ARM) and Fixed Rate Mortgage, two underlying loans of RMBS, as well. John Y. Campbell, Nuno Clara, and Joao F. Cocco [3] mentioned in their paper that stabilizing properties of plain-vanilla ARMs can be enhanced by adding an interest only option that applies during recessions, which allows borrowers to extend loan maturity. The advantages of this option include stabilizing consumption growth in a business cycle, transferring defaults into expansions, and lowering the equilibrium mortgage rate by stabilizing cash flows to lenders. Macro-economic factors also play an important role in deciding whether to choose ARM or FRM. For example, James Vickery [4] points out that the choice between ARM and FRM is highly sensitive to the interest rate. A 10-basis point increase in FRM interest rates increases the probability that the household will choose an ARM by 10.4 percentage points. The high coefficient of substitution shows that the aggregate share of FRMs and ARMs are strongly correlated to the interest rate of mortgage-backed security market.

Shifting to the credit event side on mortgage-backed security, scholars also have done a lot of research on how credit losses are affected by some personal or habitual factors. JOHN Y. CAMPBELL, JOÃO F. COCCO [5] conducted research by building a model to measure how mortgage premia and default can be affected by adjustable versus fixed mortgage rates, loan-to-value ratios, and mortgage affordability. The results conclude that the default behavior can depend on both the extent to which a borrower has negative home equity and the extent to which borrowers are constrained by low current resources. Meanwhile, their study also mentioned that the higher default rate on ARM during the recent U.S housing downturn is related to the mortgage selection by heterogeneous borrowers. Another article analyzes the probability of prepayment and default on mortgage-backed securities [6]. In this article, they investigate the relation between valuation of MBS and decisions of prepayment and default. Even though MBS are typically guaranteed by financial institutions, default action can still harm its value by delaying the cash repayment period. In their research, they discovered the value of a pass-through mortgage-backed security is highly subjected to the value of its underlying mortgage house. As the value of houses declines to a certain level, the value of pass-through mortgage security will exceed it. Under this situation, the borrower of MBS is highly likely to default, which will negatively impact on the value of security. Another paper dig into the “negative equity” situation by incorporating the level of personal character. Stephen A. Atlas, Eric J. Johnson, and John W. Payne [7] examine the effect of time preferences across both initial mortgage choice and subsequent mortgage management. Assuming there is a negative housing shock, the subsequent mortgage management mainly focused on two aspects: keep holding the mortgage or decide abandoning the mortgage as known as “walking away”. One of their hypothesis states that homeowners who discount the future over the long-term more (low δ) are more likely to default on their mortgages while present-biased homeowners (low β) are less likely to default. Fortunately, this hypothesis is verified in the end. They conclude that present biased homeowners are more likely to keep their mortgage instead of defaulting or prepaying. In contrast, discounting of future type consumers is more willing to walk away under the same situation. Additionally, in the book “Debt Markets and Investments”, MingWei Liang and Milena [8] deem the most important factor determines the prepayment is refinancing, suggesting that the level of market interest plays a significant role. The second important factor for prepayment is relocation, in the other word “life event of the home buyers”, including employment change, marriage, divorce, and change in family size. All these factors are crucial to buyers on how they manage their mortgage. Besides that, the author mentions that home buyers will typically follow a relatively predictable pattern based on the loan age when they decide to prepay. For instance, during the early stage of the loan, the speed of prepay usually increases. The authors of the chapter also state that prepayment rate follows seasonality as higher prepayment rates are observed during the summer.

Concluding the previous research, it is found that macroeconomic factors can influence MBS by changing the odds of the prepayment rate and default rate. Meanwhile, macroeconomic factors can also influence people’s preferences regarding mortgage type choice and ability to make mortgage repayments. Previous research also exhibited that credit loss can be triggered by personal factors and mortgage status such as family size, heterogeneity of house buyers, time preferences of buyers, mortgage age, mortgage interest rate, and underlying house value. However, preceding articles hardly focus on how macroeconomic factors can directly influence credit loss. Therefore, a model is desired that can input macroeconomic factors and output credit loss in quantification. It is considered important to conduct quantifying research into credit loss for three reasons. First, the U.S. mortgage-backed securities (MBS) market is one of the world's largest and most liquid fixed-income markets, with a market size exceeding $12 trillion. Credit losses may lead to a chain reaction and trigger systemic risks (such as the 2008 financial crisis). Also, institutions such as banks, insurance companies, and pension funds hold a large amount of MBS, and credit losses directly affect their capital adequacy ratio and solvency. Secondly, credit loss is a core factor in the pricing of MBS, directly affecting yields and spreads (such as the spread between MBS and Treasury bonds). Investors need to accurately assess credit risks to set reasonable prices. Thirdly, credit losses have led banks to tighten mortgage standards, reduce real estate demand, further depress house prices, and form a vicious circle. Studying credit losses can help predict the inflection point of the real estate market. The most intuitive and unavoidable factors that can impact the credit loss in the MBS market are believed to be macroeconomic factors. Currently, an era of declining macroeconomic capacity is being experienced, which means the potential financial risk that might explode anytime cannot be ignored. The downgrade of consumption power and increase of unemployment rate suggest that home buyers are exposed to financial trouble that could hinder them from paying the constant cash flow in the MBS market. Thus, in this article, these macro-economic factors will be utilized to research how much and how the credit loss will be affected.

3. Model and results

The objective is to examine how macroeconomic factors lead to mortgage defaults. First, 40 years of data for GDP growth, inflation, unemployment rate, Average Sales Price of Houses Sold for the United States, number of households, disposable income, 3-month t-bill rate, and 10 years treasury yield are collected. The data is analyzed, and a VAR model is built. To check the performance of the model, a comparison of models with lag 1 and lag 2 is conducted by running ACF, PACF, and roots. Eventually, it is found that the model with lag2 has stronger performance, and model equations are set up for each individual macroeconomic factor. After that, the forecasting equation is used to simulate the loan-to-value and debt-to-income ratio (DTI), which serve as the two yardsticks to decide the default behavior.

Source: Federal Reserve Bank of St. Louis

*t_1 stands for period t-1

*t_2 stands for period t-2

*t1 stands for period t+1

For the LTV, this is the ratio of how much the size of the loan respects the value of the property. The value of the property is assumed to be the same as the average sales prices of houses sold for the United States in this case. Since the lag 2 model equations of each macroeconomic condition are available, these equations can be used to forecast the future 30 years' average sales price of houses sold for the United States. As the model equation is lag 2, the real-world data of both t-1 and t-2 must be input into the model (t represents the period of time) to forecast the average sales price of houses sold for the United States for periods t, t+1, t+2…t+359. The error of the regression is assumed to come from a standard normal distribution. To do that, errors are continuously drawn from this distribution, using the coefficients and lag variables to propagate the average housing price over time. 1000 random numbers from N (0,1) are obtained and added to the average sales prices of houses sold for the United States for each forecasted period. Finally, 1000*360 house prices are obtained, which are also the value of property in the LTV.

$$ \mathrm{L}\mathrm{o}\mathrm{a}\mathrm{n}\mathrm{ }\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{V}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{ }\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}=\frac{\mathrm{L}\mathrm{o}\mathrm{a}\mathrm{n}\mathrm{ }\mathrm{V}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}{\mathrm{ }\mathrm{V}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{H}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e}}$$(1)

$$ errors <- rnorm(num\_errors, mean = 0, sd = 1)$$(2)

Next, the value of the property is used to get the loan value. The starting point of LTV is set to be 0.7. Therefore, the first period of the 1000 property values, multiplied by 0.7, is used to calculate the starting loan value. As is known, the loan value will decay with a regular amortization schedule until 0 at the end of 360 periods. Therefore, the interest rate is set equal to the current average 30-year fixed mortgage rate, and the formula is derived to calculate how much the loan will amortize in each period. Eventually, 1000*360 loan values are obtained, which correspond to the property value one by one. For the last step, loan value is divided by property value to get 1000*360 LTVs.

DTI is the debt-to-income ratio, representing debt payment divided by rental income. In this simulation, the debt payment can be easily calculated with the loan value obtained from the LTV equation, which is the constant monthly payment (principal + interest). However, rental income needs to be forecasted based on the economic indicators derived from the VAR model. To achieve this, 7 years of data on rental income per unit, GDP, unemployment rate, Average sales prices of houses sold in the United States, and number of households are collected. Similar to the LTV forecast, these variables are run in the VAR model to acquire equations for rental income per unit. After that, the rental income for future 360 periods can be forecasted by using the model equation of each macroeconomic indicator. Additionally, 1000 errors from N(0,1) need to be randomly generated and added individually to each period of rental income. Thus, 1000 rental incomes with errors will be obtained for each future period. Finally, 360,000 constant monthly payments are divided by 360,000 rental incomes to obtain the DTIs.

$$ \mathrm{D}\mathrm{e}\mathrm{b}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{I}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{ }\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}=\frac{\mathrm{D}\mathrm{e}\mathrm{b}\mathrm{t}\mathrm{ }\mathrm{P}\mathrm{a}\mathrm{y}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}{\mathrm{R}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{I}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}}$$(3)

Source:Federal Reserve Bank of St. Louis

*t_1 stands for period t-1

*t_2 stands for period t-2

*t1 stands for period t+1

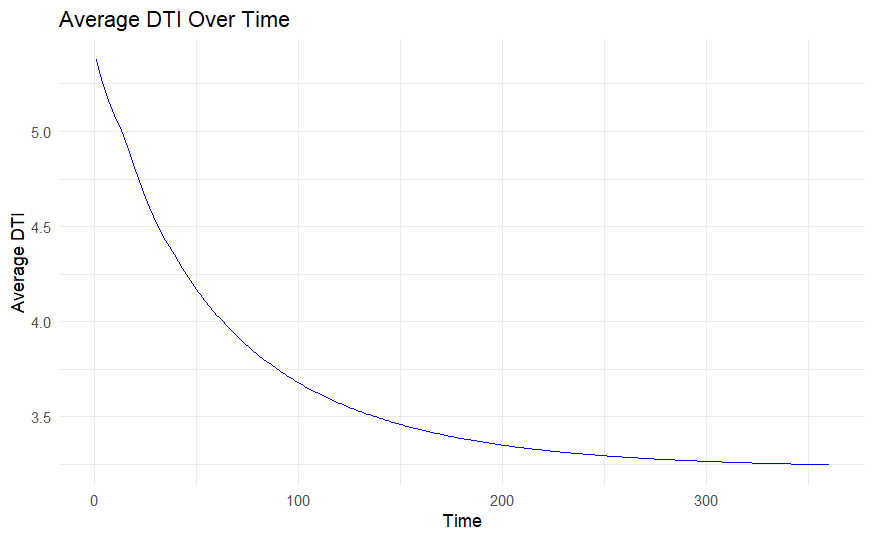
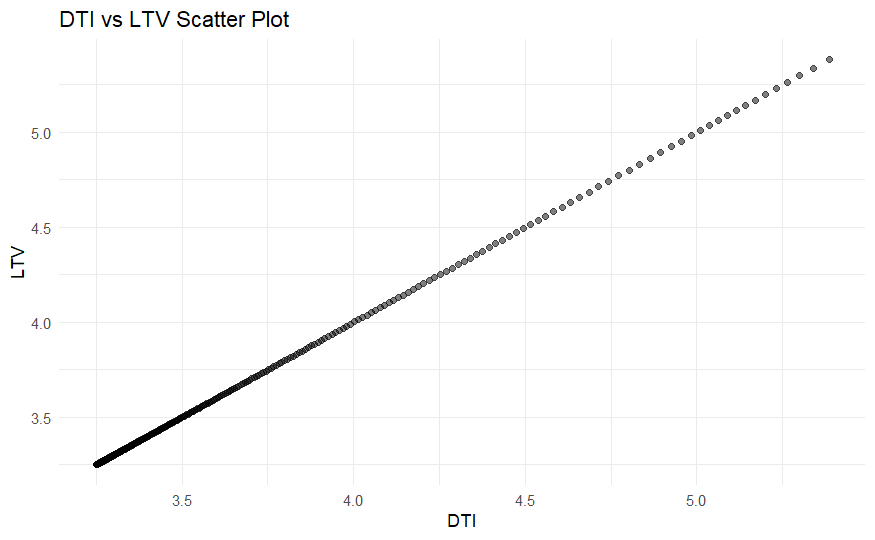
After the DTIs and LTVs are computed, Average DTI over time, Average LTV over time, and DTI vs LTV scatter plot are plotted, revealing a strong correlation with each other.

The last step is the credit loss analysis. A borrower defaulting on a specific LTV/DTI combination is hypothesized. Theoretically, the realized loss (severity) will be the leftover amount in this mortgage (the unpaid balance at default), minus the value of the house if it's auctioned (usually 50% of the current value) since this is retained. The realized loss also needs to include loss in interest, which is the unpaid balance times monthly interest rate times the months left. To calculate the credit loss, the probability of each LTV/DTI combination needs to be determined. First, the smallest and biggest LTV and DTI among the matrices are found. Then, the difference between the smallest and biggest LTV is separated into five even intervals, as well as DTI. After that, the number of LTV/DTI combinations that fall into those LTV/DTI intervals are checked. These numbers are counted in each interval and divided by 360,000, which is the total number of LTV/DTI combinations, to obtain the probability of each interval. For the last step, the average realized loss is multiplied by the probability of each interval, resulting in the credit loss for each interval.

4. Conclusions

For lenders, LTV and DTI are two crucial indicators that must be taken into consideration. The loan to value ratio helps investors to measure how much of a property’s value is borrowed so that they can assess the risk of the loan. The debt-to-income ratio helps investors to understand how much of the income of borrowers will be paid as debt payment.

In this study, credit loss is simulated under different LTV/DTI values by running VAR models for various macroeconomic factors. The results show that when the DTI is fixed within the range of 3.0243 and 3.50345, the credit loss increases as the LTV interval goes up. The credit loss reaches the maximum value when DTI is within the range of 3.0243 and 3.50345, and LTV is within the range of 0.5858023 and 0.7322529. When LTV is fixed within the range of 0.5858023 and 0.7322529, the credit loss declines as the DTI interval goes up. The credit loss reaches the minimum value when LTV is within the range of 0.5858023 and 0.7322529, and DTI is within the range of 4.940898 and 5.420048. However, it is interesting that all credit loss is centered when DTI is within the bucket of 3.0243 and 3.50345. Except when LTV is within the highest bucket, no credit loss is found when DTI is greater than 3.50345.

Three conclusions are drawn from this analysis. First, an increase in LTV undoubtedly leads to an increase in credit losses. Secondly, when LTV is high, the increase in DTI will further amplify the credit loss. Thirdly, in the case of low LTV, the change in DTI has little impact on credit losses (almost no change). These conclusions correspond to the financial logic in the real world, as when the borrower has a low-down payment (high LTV) and a high debt level (high DTI), both the chance of a credit event and the amount of credit loss will increase significantly.