1. Introduction

Seeking risk control portfolio strategies adapted to market changes is a concern for most investors. The classical Markowitz mean-variance optimization model achieves static control of risk. However, under the condition of real-time market changes, the static model fails to capture the market change factors. Therefore, its effect may be weakened as the market changes [1]. In order to adapt to the dynamically changing market environment and enhance the robustness of the strategy, this study innovatively introduces a dynamic risk-adjusted portfolio strategy, which has the advantage of designing the degree of risk aversion according to the market environment [2], balancing the risk and return, and realizing a more flexible portfolio strategy.

Risks in real markets are thick-tailed and non-normally distributed. Additionally, traditional variance-based risk control cannot effectively control extreme risks. Therefore, this study utilizes a loss percentile-based metric CvaR to measure tail risks. Moreover, CvaR has convexity and consistency, which is easy to linearize for the optimal solution. This study computes the value of CvaR and assigns an upper bound to control the tail losses. Given the fact that CvaR risk control strategy is highly sensitive to the selection of the confidence level  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ , some studies have proposed to set the upper threshold for the tail loss at multiple confidence levels simultaneously to achieve the control of tail risk [3]. Nevertheless, traditional studies have set uniform thresholds for multiple  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ . The degree of investor avoidance is non-uniform for different levels of  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ . Besides, the uniform thresholds are prone to excessive constraints for the high level of  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ . For the low level of  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ , it is easy to linearize and find the optimal solution. Over-constraints on high level  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ , and the constraints on low level  $$ {\mathrm{\beta }}_{\mathrm{k}}$$  are ineffective. Therefore, a finer risk control strategy should be set. Based on this, this study extends to give the differentiated upper bound thresholds of CvaR values at different confidence levels to enhance the applicability and robustness of the model.

Comprehensive dynamic adjustment and differential control of risk under multiple differentiated  $$ {\mathrm{\beta }}_{\mathrm{k}}$$ . This study introduces the Chicago Board Options Exchange volatility index VIX. The conditional stock market variance in the VIX index not only has a good predictive ability of future stock price volatility, and is strongly negatively correlated with the risk of the tail event [4]. Consequently, this study constructs a linear scaling function based on the VIX index, adjusting the Cvar according to the market risk level threshold value. Moreover, the strength of tail loss control is different in different environments, which can realize flexible adjustment according to the market environment.

In summary, the multiple differentiated thresholds are set according to the market risk. Additionally, the multiple thresholds are dynamically adjusted by introducing a linear scaling function with a VIX index in order to maximize the return and minimize the cost, where the transaction cost is calculated by the L1 regularization term. Finally, the effectiveness of the strategy is evaluated in terms of risk-adjusted returns and maximum retracement.

2. Method

This study builds on traditional risk control models by introducing a method that adjusts the CVaR upper bound through linear scaling based on the VIX index, allowing the strategy to better adapt to changing market conditions.

2.1. Dynamic portfolio optimization based on differentiated multiple β-CvaR

Firstly $$ ,\mathrm{w}={({\mathrm{w}}_1,{\cdots ,\mathrm{w}}_{\mathrm{n}})}^{\mathrm{T}}$$ is defined as the weight of each stock in the investment pool, $$ \mathrm{r}={({\mathrm{r}}_1,{\cdots ,\mathrm{r}}_{\mathrm{n}})}^{\mathrm{T}}$$ is the return of each stock,  $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ is the confidence level, and  $$ \mathrm{\alpha }=-{\mathrm{w}}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}\mathrm{ }}$$ is the loss at the quantile $$ {\mathrm{ }\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ .

Treatment of CvaR values according to the linearization approach [3]:

$$ \mathrm{F}\left(\mathrm{w},\mathrm{\alpha }\mathrm{\beta }\right)=\mathrm{\alpha }+\frac{1}{(1-\mathrm{\beta })}\sum _{\mathrm{t}=1}^{\mathrm{N}}\mathrm{E}{[-{\mathrm{w}}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}}-\mathrm{\alpha }]}^{+}$$(1)

After linear optimization [5], the CvaR expression is transformed into a convex function with respect to the weights, which facilitates the use of linear programming to solve for the optimal weights.

Determine the upper bound threshold for multiple differentiated  $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ :

$$ \mathrm{F}\left(\mathrm{w},\mathrm{\alpha }{\mathrm{\beta }}_{\mathrm{k}}\right)\le \mathrm{C}+{\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}$$(2)

For multiple  $$ {\mathrm{\beta }}_{\mathrm{k}}$$  , set the center threshold  $$ \mathrm{C}=0.15$$  and set different offsets  $$ {\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}$$  for different levels of  $$ {\mathrm{\beta }}_{\mathrm{k}}$$  [3], The collation is obtained:

$$ {\mathrm{\alpha }}_{\mathrm{k}}+\frac{1}{\mathrm{N}(1-{\mathrm{\beta }}_{\mathrm{k}})}\sum _{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{u}}_{\mathrm{t}\mathrm{k}}\le \mathrm{C}+{\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left(\mathrm{t}\right)$$(3)

$$ {\mathrm{u}}_{\mathrm{t}\mathrm{k}}=\sum _{\mathrm{t}=1}^{\mathrm{N}}{[-{\mathrm{w}}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}}-\mathrm{\alpha }]}^{+}$$(4)

 $$ \mathrm{k}=\mathrm{1,2},\mathrm{3,4},5$$  corresponds to the confidence level(95%,96%,97%,98%,99%), respectively, and the initial deviation  $$ {\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left({\mathrm{t}}_0\right)=\left(\mathrm{0.005,0.0075,0.01,0.015,0.02}\right)$$  for a given multiple differentiated  $$ {\mathrm{\beta }}_{\mathrm{k}}=\left(\mathrm{0.05,0.04,0.03,0.02,0.01}\right)$$ 

To determine the upper limit of dynamic risk tolerance based on market risk, this study introduces the following linear scaling formula:

$$ {{\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left(\mathrm{t}\right)=\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left({\mathrm{t}}_0\right)(1-\mathrm{\rho }\frac{{\mathrm{V}\mathrm{I}\mathrm{X}}_{\mathrm{t}-1}-\stackrel{-}{\mathrm{V}\mathrm{I}\mathrm{X}}}{\stackrel{-}{\mathrm{V}\mathrm{I}\mathrm{X}}})$$(5)

Where  $$ {\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{K}}}\left({\mathrm{t}}_0\right)$$  is the initial deviation,  $$ \mathrm{\rho } $$ is the risk tolerance scaling factor, and $$ \mathrm{ }\stackrel{-}{\mathrm{V}\mathrm{I}\mathrm{X}\mathrm{ }}$$ is the average value of the VIX index over the formation period.

Determine the maximized rate of return with minimized L1 regularized transaction costs:

$$ \mathrm{max }{\sum }_{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{w}}_{\mathrm{N}+1}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}}-\mathrm{\lambda }{\sum }_{\mathrm{i}}^{\mathrm{n}}\left|{\mathrm{w}}_{\mathrm{N}+1,\mathrm{i}}-{\mathrm{w}}_{\mathrm{N},\mathrm{t}}\right|$$(6)

Where  $$ \sum _{\mathrm{i}}^{\mathrm{n}}\left|{\mathrm{w}}_{\mathrm{N}+1,\mathrm{i}}-{\mathrm{w}}_{\mathrm{N},\mathrm{i}}\right|$$  is the sum of asset turnover rates using L1 regularization, and  $$ \mathrm{\lambda }\mathrm{ }$$ is the transaction cost coefficient used to calculate the transaction cost due to weight resetization in periods N to N+1.

The collation is obtained:

$$ \max \mathrm{ }{\sum }_{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{w}}_{\mathrm{N}+1}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}}-\mathrm{\lambda }{\sum }_{\mathrm{i}}^{\mathrm{n}}\left|{\mathrm{w}}_{\mathrm{N}+1,\mathrm{i}}-{\mathrm{w}}_{\mathrm{N},\mathrm{t}}\right|$$(7)

Subject to:

$$ {{\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left(\mathrm{t}\right)=\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left({\mathrm{t}}_0\right)\left(1-\mathrm{\rho }\frac{{\mathrm{V}\mathrm{I}\mathrm{X}}_{\mathrm{t}-1}-\stackrel{-}{\mathrm{V}\mathrm{I}\mathrm{X}}}{\stackrel{-}{\mathrm{V}\mathrm{I}\mathrm{X}}}\right)\mathrm{ }$$

$$ {\mathrm{\alpha }}_{\mathrm{k}}+\frac{1}{\mathrm{N}\left(1-{\mathrm{\beta }}_{\mathrm{k}}\right)}\sum _{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{u}}_{\mathrm{t}\mathrm{k}}\le \mathrm{C}+{\mathrm{C}}_{{\mathrm{\beta }}_{\mathrm{k}}}\left(\mathrm{t}\right)\mathrm{ }$$

$$ {\mathrm{u}}_{\mathrm{t}\mathrm{k}}=\sum _{\mathrm{t}=1}^{\mathrm{N}}{[-{\mathrm{w}}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}}-\mathrm{\alpha }]}^{+}$$(8)

$$ {\mathrm{u}}_{\mathrm{t}\mathrm{k}}\ge -{\mathrm{w}}^{\mathrm{T}}{\mathrm{r}}_{\mathrm{t}}-\mathrm{\alpha }\mathrm{ }$$

$$ {\mathrm{u}}_{\mathrm{t}\mathrm{k}}\ge 0\mathrm{ }$$

$$ 1^{\mathrm{T}}{\mathrm{w}}_{\mathrm{N}+1}\ge 1\mathrm{ }$$

$$ {\mathrm{w}}_{\mathrm{N}+1}\ge 0$$

2.2. Dataset

In the experiment, this study employs two representative datasets: the Fama-French 25 Portfolios (FF25) and the GICS Sector Portfolio 11 (GSP11). For the FF25 dataset, monthly returns from 1979 to 1998 are used as in-sample data, while returns from 1999 to 2018 serve as out-of-sample data. For the GSP11 dataset, monthly returns from 1989 to 2009 are used for model training, and data from 2010 to 2020 are used for out-of-sample testing.

The in-sample data is used to train the model and determine the optimal risk tolerance scaling factors. The model is then applied to the out-of-sample period to evaluate its performance. Both datasets are structurally representative: FF25 reflects cross-sectional differences in asset styles and does not require data cleaning for delisting or missing values, offering a stable and long-term return series. GSP11 captures sector-level asset allocation patterns and reflects real-world market behavior through industry rotation.

Together, the two datasets provide structurally distinct views of the market—one based on style factors and the other on industry sectors—allowing for a comparative analysis of model performance under different market environments.

3. Result

This study sets up four groups for comparative analysis, as can be seen in table 1.

To evaluate model performance, we determine the optimal risk tolerance scaling factors $$ \mathrm{\rho }=2 $$ for the FF25 dataset and $$ \mathrm{\rho }=6 $$ for the GSP11 dataset, along with a set of multiple differentiated  $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ thresholds centered around  $$ \mathrm{C}=0.15$$ , and transaction cost coefficients $$ \mathrm{\lambda }=0.01$$ .

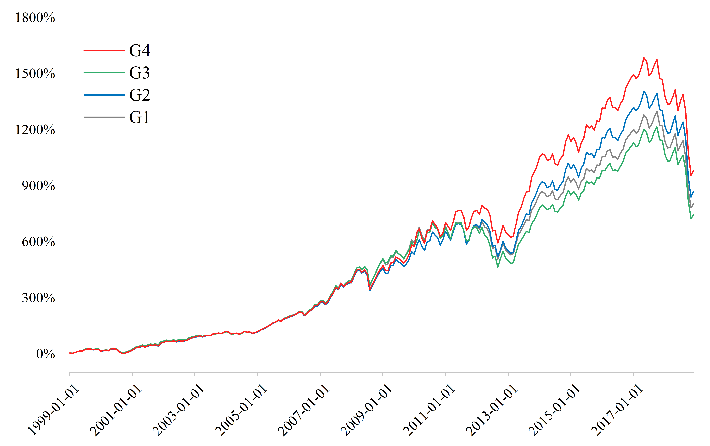
As shown in Figure 1, applying only differentiated thresholds across multiple differentiated $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$  (Group G2) does not yield significant improvement in cumulative returns compared to the control group (G1), and in some cases, performance even declines. Similarly, using only dynamic thresholds (Group G3) results in no notable difference from G1. In contrast, the combination of dynamic adjustment and multiple differentiate $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ (Group G4) leads to a significant improvement in cumulative returns relative to G1. This indicates that a strategy incorporating both dynamic scaling and multiple differentiated  $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ is more responsive to market conditions and delivers superior performance.

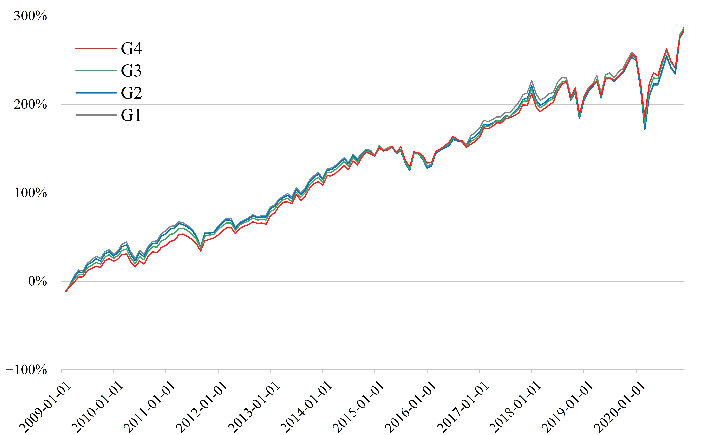
However, Figure 2 shows no statistically significant differences in cumulative returns across all three experimental groups (G2, G3, and G4) compared to the control group, suggesting that the effectiveness of the strategy may depend on the specific dataset or market environment.

Table 2 and Table 3 show that the risk-adjusted returns (Sharp Ratio) of the strategies on both datasets are significantly improved when the market risk-free rate is 2%.

Table 2 shows that the strategies improve the Sharp Ratio by increasing the excess return of the portfolio. The FF25 dataset features strong heterogeneity across assets, leading to varying sensitivities to market conditions [6]. In particular, small-cap assets may have potential excess returns when the market declines. Therefore, the strategy differentiation threshold setting is manifested in the enhanced ability to capture excess returns.

Table 3 shows that in the GSP11 dataset, the strategy improves the Sharpe ratio by decreasing the volatility of the portfolio return because the data structure of the GSP11 dataset exhibits stronger risk structuring and consistency. Therefore, the strategy is more sensitive to common risk prevention and control, and reduces volatility.

In the two datasets, the strategy acts in different ways, but both significantly increase the Sharpe ratio of the portfolio, indicating that the strategy has good cross-market applicability.

4. Discussion

In this study, four groups of experiments are set up. The differentiated thresholds can optimize the model's ability to respond to different scenarios and accurately regulate risks. Additionally, dynamically change the weights to improve the strategy's ability to respond to market changes. The strategy combines both approaches, using dynamically adjusted differentiated thresholds to achieve multiple levels of flexible risk control. Consequently, a higher confidence level has a higher elasticity in the face of market changes. Therefore, the model takes into account both the release of revenue and risk control. In addition, the VIX index signals are forward-looking, which helps adjust risk exposure in advance, mitigating potential tail events. This also smooths portfolio rebalancing, reducing transaction costs [7], and ultimately improves the strategy’s risk-adjusted performance.

In the multiple differentiated $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ dynamic adjustment strategy, maximum drawdown shows relatively poor performance. During dynamic adjustment, excessive risk exposure may lead to an increase in drawdowns. In addition, applying multiple differentiated $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ at the same time can lead to a more complex and less tractable structure of risk constraints. Therefore, the optimizer stability decreases and ultimately may lead to risk control bias [8], resulting in the setting of the unbalanced tail distribution. The effectiveness of multiple strategies is usually based on a “reasonable tail distribution”, an unbalanced distribution will lead to an increase in the maximum retracement and volatility of the strategy [9].

Excessive constraint conditions in CVaR optimizers may lead to a decline in solver stability. To address this issue, the differentiated constraints under multiple  $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }} $$ levels can be integrated into a multi-objective optimization framework, thereby mitigating the potential infeasibility or instability caused by conflicting constraints under distributional uncertainty [10], and enhancing the overall performance of the strategy. Meanwhile, the CVaR metric may result in excessive concentration on tail losses, which in practice can expose the strategy to high maximum drawdown risk. To improve this issue, one can incorporate path-dependent risk into the CVaR linear programming formulation [11], constructing a joint optimization objective that captures both aspects. Additionally, a Wasserstein-based distributionally robust optimization approach can be employed to further account for distributional uncertainty and enhance the robustness and effectiveness of the strategy.

5. Conclusion

The dynamic adjustment strategy based on multiple differentiated risk thresholds significantly enhances the risk-adjusted returns of investment portfolios. However, its performance varies across different datasets. In the FF25 dataset, characterized by style-based asset rotation and high cross-sectional heterogeneity, the strategy’s differentiated thresholds enable the selection of assets that combine controllable tail risk with strong upside potential. By leveraging asset heterogeneity and market fluctuations, the strategy adjusts the portfolio composition in a way that preserves return potential while managing risk, thereby significantly improving excess returns. On the GSP11 dataset of industry rotation, the correlation of industry indices is high. Based on this asset characteristic, the strategy can effectively identify the risk consistency characteristics of asset structuring and realize risk consistency control, thus significantly reducing the volatility level and tail risk exposure of the strategy. In different datasets, the model takes into account multiple differentiated $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ and market movements. This allows the strategy to respond asymmetrically to changes in market conditions. As a result, its adaptability and robustness are significantly improved.

The model performs poorly in terms of the maximum retraction rate because the dynamic threshold has the risk of exposing higher risk exposures. Additionally, the differential risk constraints on the multiple differentiated $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$  increase the complexity of the model, which decreases the performance of the optimizer and is prone to optimization failure. To address this problem, the discretization constraints under multiple differentiated $$ {\mathrm{\beta }}_{\mathrm{k}\mathrm{ }}$$ can be integrated into multi-objective optimization. Besides, a portfolio optimization model combining robust CVaR with maximum retraction control can be utilized to improve optimizer stability.