1. Introduction
Until April 2024, there were 5.44 billion internet users worldwide, which amounted to 67.1 percent of the global population. More detailly, 62.6 percent of the world's population were social media users [1]. Online video platforms like YouTube, Netflix, Hulu, and Amazon Prime have become dominant in the digital media landscape. They offer a vast array of content, from user-generated videos to professionally produced series and movies. There are specific areas within audiovisual content markets where YouTube exerts considerable competitive pressure on both Netflix and classic TV, for instance, through prime-time video entertainment [2].
Multi-homing refers to the capability of supporting multiple platforms. This means that the production of products can support more than one platform. For instance, usually, one single TV plays can be viewed on different online video platforms. On the other hand, single-homing can only support one platform, this is because the copyright of a TV play is sold to a single platform. In this case, our study aimed to figure out in what situation, the profit of online video platforms can be maximized, multi-homing product or single-homing.
Armstrong analyzed equilibrium when two platforms compete in single-homing. Research indicates that platforms exert monopoly power if consumers can multi-home on one side and compete with sa ingle-homing side [3]. Belleflamme & Peitz analyze the impact of multi-homing on one side on prices, platform profits, and buyer and seller surplus. Further, they investigate the impact of the possibility of multi-homing on the competition between two-sided platforms [4]. Consequently, the importance of studying platforms competition when both multi-home has been recognized.
Multi-product search model can affect a firm's price decisions significantly, and discussed few possible applications of their model [5]. He suggests that if consumers' valuation surplus from sampling the second firm is smaller than the search cost, consumers will stop searching:
This is similar to one of the assumptions we make: If the sum of the valuation of all the products F1 hosts is bigger than the membership fee of F1, then the consumer will pay the membership fee.
(VA+VB>=P1)
In addition, Rochet and Tirole presented seminal work on platform competition in two-sided markets with regard to pricing strategies and network effects when the two sides of the market interact through a platform [6]. Essentially, they pointed out that platforms must equilibrate pricing between the two parties so that maximum participation can ensure maximal profits [7]. If multi-homing, where one player or both home more than one platform, as done by Belleflamme & Peitz, is taken into consideration, then basically, the competitive dynamics change [4]. It may lead to consumer surplus and gain through multi-homing on both sides, resulting in more intense competition, which lowers prices and cuts down the profit of platforms. However, such pressure pushes the platforms to innovate and make their services difficult to attract more users. Therefore, the study of platform competition in two-sided markets becomes of important significance toward understanding the broader implications of multi-homing on market structure, pricing, and consumer behavior.
Building on these foundation studies, it becomes quite evident that multi-homing dynamics have important implications for two-sided market competition [8]. Innovation and the need to make unique offerings increase manifold when consumers are able to multi-home, as it becomes a necessary condition for any platform seeking a competitive advantage. This benefits not only the consumer through enhanced service offerings but also ratchets up the competitive environment. For instance, during this process of alluring users from both sides of the market, platforms may reduce prices or add unique features that would raise consumer surplus. Also, the interplay between multi-homing and network effects is complex in pricing, as the platform has to balance the cost and benefit of both user groups. This also might reduce the profit of platforms amidst rising competition. It drives an environment of a market in which consumer choice is maximized and sustains platforms' value proposition. Understanding how multi-homing has complex effects is thus important to understand the broader implications at the economic and strategic level in two-sided markets.
The earlier research utilizes a function of quantity when searching consumer preferences in the light of consumer surplus. This study shows that Cournot equilibrium exists and corresponds to a Ramsey optimum [9]. Further, the Bertrand oligopoly is mentioned by considering the utility u(x) and obtaining the consumer surplus s(x); the profit is deduced. Unlike the Cournot model, this model allows firms to acquire different cost functions. The result indicates that in an oligopoly, multi-product pricing is one of equilibrium between firms rather than optimal by a single firm or a single decision-making.
Another paper found that the increased platform-level multi-homing of applications hurts platform sales, a finding consistent with the literature on brand differentiation, and they also find that platform-level multi-homing on platform sales' disadvantages outweighs its positive effects [10]. Moreover, it shows that seller-level multi-homing decisions are important decisions for sellers in two-sided markets. This motivated us to set up a model to find the best response for two platforms in the same market to maximize their profits.
Section 1 discusses the competition within two online video platforms, each platform holding two multi-homing products, and examines whether there is an incentive for platforms to drop one of their products. This is because if no one drops a product, then it is a Bertrand Model. This might cause the profits to become negative as the price is zero after price competition. In this situation, the probability of dropping a product or not is calculated through a mixed strategy.
For the next section, one platform holds the multi-homing product, another holds the single-homing product, and the profits of the two platforms are computed separately. We have six assumptions, but only one of them is effective, which means the result satisfies our previous condition setting. Additionally, when the platforms reach an equilibrium price, whether there is an incentive for one side or both sides of firms to lower their price has been tested.
The rest of the article is organized as follows. In Section III, the platforms obtain a single-homing product, and the maximum profit have been calculated. Then, whether there is an incentive for section II situation change in this section has been determined. Further, we examined the equilibrium price and equilibrium profit of two platforms while in this situation. In the last section, our study uses the cumulative distribution function to compute the consumer welfare in these models. The average and aggregate consumer welfare has been computed, and the market configuration showed.
2. The model
2.1. Model set-up
We consider a setting with two online video platforms,
2.2. Section I
Proposition 1: In the case of
Proof.: Any
If there is a Bertrand competition, F1 and F2 may consider dropping one of the products, A or B. Table 1 shows the profits of the two firms under different conditions.
|
F1/F2 |
Drop profit |
Non-drop profit |
|
Drop profit |
0,0 |
0.067,0.369 |
|
Non-drop profit |
0.369,0.067 |
0,0 |
(The calculation of 0.369 and 0.067 see section II. )
There is a pure strategy for the two firms because the profits after dropping a product are always higher or equal than not dropping. Our study uses a mixed strategy to find the probability to drop to maximize the profit of F1 and F2.
Calculations:
π(high) = 0.369 π(low) = 0.067 π(total)= 0.436
For F1:
Here are three situations:
(1) q > 0.1537 so p = 1
(2) q < 0.1537 so p = 0
(3) q= 0.1537 so
For F2:
Here are three situations:
(1)
(2)
(3)
Thus,
2.3. Section II
Three basic conditions for consumers to buy the product:
For F1 hosts A and B, F2 hosts B only:
For consumers who buy the product, their valuation must satisfy the following conditions.
(1) Firstly,
(2) For the next,
(3) The third condition is:
Proposition 2: For F1 hosts A and B, F2 hosts B only, the profit of F1 is higher than F2 when reaching equilibrium.
Proof:
The first assumption directly follows from Proposition 2, it is within the range of precondition we set:
Situation 1: 1>P1>P2, which is shown in Figure 1 (in the following figures, light blue represents
The profit
The profit
By setting two equations, the equilibrium price for F1 is 0.60747 and that for F2 is 0.24493.
The equilibrium profit for F1 is 0.369 and the profit for F2 is 0.067.

However, the platforms might decrease their prices to maximize their own profit, and our study group checked whether lowering down its own price for one of the platforms is beneficial for it. When F1 adjust P1 to P1'( Figure 2), the original profit is
By calculating the second order condition,
dπ12/d2P1= -2 < 0 Pi1 at equilibrium is the highest possible profit.
dπ22/d2P2=-2P1-2+6P2= -2*0.60747-2+6*0.24493=-1.74536 < 0 π2 at equilibrium is the highest possible profit.
Hence, both F1 and F2 have no incentive to lower down the price when reaching equilibrium.

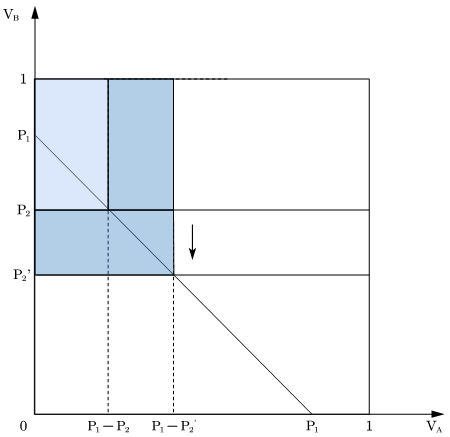
Figure 3. Consumer distribution (F2 adjust P2 to P2')
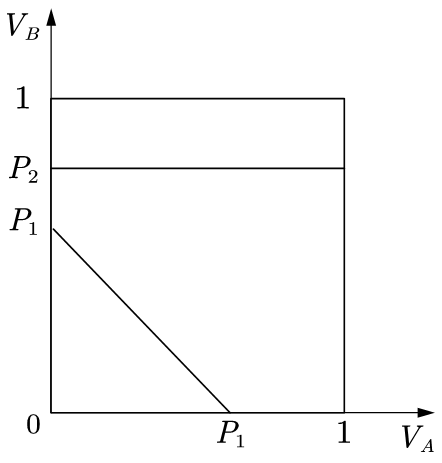
Situation 2: 1 > P2> P1, shown in figure 4.
Under this condition, P1- P2< 0, while VA is distributed between 0 and 1, and VA is always bigger than P1- P2.
This is contradict with the third condition, which means that no one will choose products from F2 since all the users consider that the consumer welfare of F1 is higher than that of F2.
Situation 3: P1 > 1 > P2 ( Figure 5)

*Since the valuation of consumers is between 0 and 1, P2(
That is to say,
By partial differentiating, the equilibriums are shown below:
Setting the two equation together, our study group gets equilibrium price P1 and P2. More specifically, the Figure 6 shows the calculation process.
The solution sets of the equations are shown on the graphs, none of intersection satisfy
This means that there is no price equilibrium in this situation.

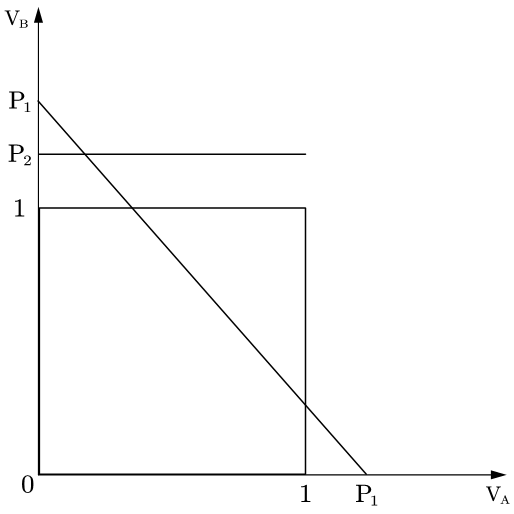
Situation 4: P1>P2>1, drawn in Figure 7.
By model setting, we assume that VB is between 0 and 1. Hence VB
In this situation, nobody will choose F2 .
F2 should not set the price of P2>1.
2.4. Section III
Proposition 3: When F1 hosts product A and F2 hosts product B, consumers are allowed to multi-home, which means they can choose to buy both products (shown in Figure 8). The equilibrium profits for the firms are the same, which is 1/4. Assuming that A and B are the same product with different valuations.
Proof:
The equilibrium price in this case is P1=P2=0.5 (they sell similar products so the prices are the same),
The equilibrium profits of both firms = 0.5*0.5=0.25
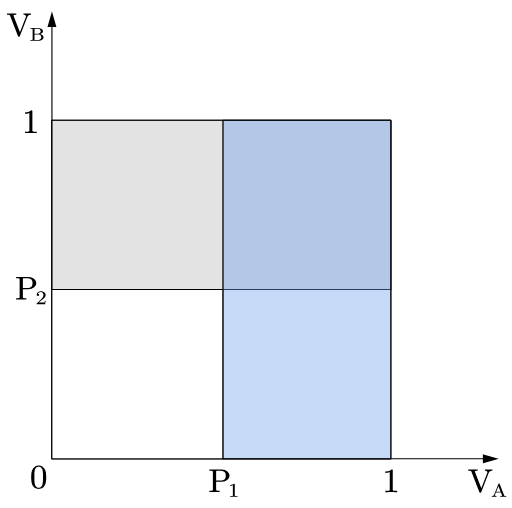
These calculations can be used to illustrate proposition 4.
As we have proved before, the two platforms have an incentive to drop a product from the situation of
Proposition 4: When F1 hosts products A and B, F2 hosts only product B. This will be the market equilibrium. F1 has no incentive to drop either product.
Proof:
Considering the case of F1 dropping product A, then they both hold product B. It comes to a Bertrand competition again, the same as the proof in proposition 1, which leads to a profit of 0. Hence F1 won't drop product A.
If F1 chooses to drop product B, the equilibrium profit equals 0.25, as we prove in proposition 3. It is still lower than 0.369.
|
A |
B |
A+B |
|
|
A |
0,0 |
0.25, 0.25 |
0.067, 0.369 |
|
B |
0.25, 0.25 |
0,0 |
0.067, 0.369 |
|
A+B |
0.369, 0.067 |
0.369, 0.067 |
0,0 |
Table 2 underline the best response for F1 and F2 is that one hosts two product and another hosts one product.
2.5. Section IIII
Proposition 5: the average consumer welfare in 'A&B vs. B' is higher than 'A vs. B'
Proof:
the profit π1=(1-P1)P1 dπ1/dP1=1-2P1=0 , so P1=1/2. Because VA ~[0,1], f(VA )=1.
Aggregate consumer welfare: 'A&B vs B' - 0.35934
Calculation:
Average consumer welfare (by using double integration):
Firm 1: Pr(purchase)
Aggregate consumer welfare:
Aggregate consumer welfare: 'A vs B' - 0.1875
Calculation:
Average consumer welfare (given that buying the product) :
Aggregate consumer welfare:
Market configuration: When one firm hosts A and B and another firm hosts only one of the products, the aggregate consumer welfare is the highest, which is 0.3593. Also, in this case, there is no motivation for F1 to drop a product. Hence, the market configuration is most likely to be one firm hosting A and B and another firm hosting only one of the products.
3. Discussion and evaluation
We set up a model and calculate to find the best strategy in a duopoly market which the platforms in it can choose to multi-homing or single-homing. Although our model has many interesting implications, it still has several limitations. Firstly, the network effect parameter still needs to be set since network effects change consumers' choices strongly. Moreover, consumer preference for products A and B is not taken into consideration, leading to the ineffectiveness of the model when applied to real cases. Additionally, we suppose that products A and B are exactly the same. However, it is nearly impossible to find two identical products because different types of consumers have their tastes in the two products when applied in the real market. our model only considers the video platform side; actually, the video producers can choose to sell the copyright of the films to which platforms. Finally, the process of how A and B enter the platform hasn't been evaluated. This is a crucial factor that indicates which platform holds both multi-homing products and single-homing products, F1 or F2.
4. Conclusion
In our paper, we have developed a model that consists of consumers' valuation and the cost of being a member of the platform, and we compare the differences between consumers' valuation and membership fee under different strategies to find the best choice of strategies for video platforms - which product (films or TV series) to host and how to set the membership fee. If they both host products A and B initially, that is a Bertrand competition, and they should use a mixed strategy to drop one product to maximize their profits. Since the equilibrium profit of firm 1 under the market structure 'firm 1 hosts product A, firm 2 hosts product B' is 0.25 (lower than 0.369), firm 1 has no incentive to drop a product. The result shows that 'firm A hosts product A and B, firm B hosts only product B' is the best strategy for the two firms. Also, when this kind of market structure happens, the platform that hosts two products should set a price of 0.6074, and the other firm should set a price of 0.245 to maximize its profits. We also calculate the average consumer welfare under different market structures. Among them, the highest average consumer welfare occurs under the market structure of 'firm A hosts product A and B, firm B hosts only product B', which is 0.3593. Consumers benefit the most in this case so perhaps some laws will be made by the government if it wants to reach the highest consumer welfare.
Future work may examine the distribution of consumers' valuation since consumers have personal preferences. Our group aims to combine more real-life cases, test the model's availability, and lean on reality based on corrections such as network effect coefficients.
References
[1]. Ani Petrosyan. (2024). Worldwide internet user penetration from 2014 to July 2024
[2]. Budzinski, O., Gaenssle, S., & Lindstädt-Dreusicke, N. (2021). The battle of YouTube, TV and Netflix: an empirical analysis of competition in audiovisual media markets. SN Business & Economics, 1(9), 116.
[3]. Armstrong, M., & Vickers, J. (2010). Competitive non-linear pricing and bundling. The Review of Economic Studies, 77(1), 30-60.
[4]. Belleflamme, P., & Peitz, M. (2019). Platform competition: Who benefits from multihoming?. International Journal of Industrial Organization, 64, 1-26.
[5]. Zhou, J. (2014). Multiproduct search and the joint search effect. American Economic Review, 104(9), 2918-2939.
[6]. Rochet, J. C., & Tirole, J. (2003). Platform competition in two-sided markets. Journal of the european economic association, 1(4), 990-1029.
[7]. Li, J., Gong, S., & Li, X. (2023). Co-Opetitive strategy optimization for online video platforms with multi-homing subscribers and advertisers. Journal of Theoretical and Applied Electronic Commerce Research, 18(1), 744-764.
[8]. Bakos, Y., & Halaburda, H. (2020). Platform competition with multihoming on both sides: Subsidize or not?. Management Science, 66(12), 5599-5607.
[9]. Armstrong, M., & Vickers, J. (2018). Multiproduct pricing made simple. Journal of Political Economy, 126(4), 1444-1471.
[10]. Vardit Landsman & Stefan Stremersch (2011). Multihoming in Two-Sided Markets: An Empirical Inquiry in the Video Game Console Industry. Journal of Marketing, Vol. 75 (November 2011), 39–54
Cite this article
Luo,D.;Song,X. (2025). Competitions Between Online Video Platforms: Multi-Homing or Single-Homing?. Advances in Economics, Management and Political Sciences,215,64-75.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 4th International Conference on Financial Technology and Business Analysis
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Ani Petrosyan. (2024). Worldwide internet user penetration from 2014 to July 2024
[2]. Budzinski, O., Gaenssle, S., & Lindstädt-Dreusicke, N. (2021). The battle of YouTube, TV and Netflix: an empirical analysis of competition in audiovisual media markets. SN Business & Economics, 1(9), 116.
[3]. Armstrong, M., & Vickers, J. (2010). Competitive non-linear pricing and bundling. The Review of Economic Studies, 77(1), 30-60.
[4]. Belleflamme, P., & Peitz, M. (2019). Platform competition: Who benefits from multihoming?. International Journal of Industrial Organization, 64, 1-26.
[5]. Zhou, J. (2014). Multiproduct search and the joint search effect. American Economic Review, 104(9), 2918-2939.
[6]. Rochet, J. C., & Tirole, J. (2003). Platform competition in two-sided markets. Journal of the european economic association, 1(4), 990-1029.
[7]. Li, J., Gong, S., & Li, X. (2023). Co-Opetitive strategy optimization for online video platforms with multi-homing subscribers and advertisers. Journal of Theoretical and Applied Electronic Commerce Research, 18(1), 744-764.
[8]. Bakos, Y., & Halaburda, H. (2020). Platform competition with multihoming on both sides: Subsidize or not?. Management Science, 66(12), 5599-5607.
[9]. Armstrong, M., & Vickers, J. (2018). Multiproduct pricing made simple. Journal of Political Economy, 126(4), 1444-1471.
[10]. Vardit Landsman & Stefan Stremersch (2011). Multihoming in Two-Sided Markets: An Empirical Inquiry in the Video Game Console Industry. Journal of Marketing, Vol. 75 (November 2011), 39–54









