1. Introduction

In the realm of educational technology and research, the development and application of student models have become increasingly sophisticated. Central to this evolution is the exploration of various dimensions that constitute these models. One critical aspect is the temporal effect, which delineates whether skills are considered static or evolve over time. This differentiation plays a pivotal role in the model's ability to accurately reflect a student's learning trajectory.

Static models, such as the Item Response Theory (IRT), assume that a student's skill level is a time-invariant trait. These models are typically employed in standardized testing scenarios, where a snapshot of student proficiency is required. However, they lack the dynamism to account for the fluid nature of learning, where a student's skill level can evolve with each educational interaction.

On the other hand, dynamic models like Knowledge Tracing (KT) present a more nuanced view. KT models account for the temporal variations in a student's skill level, adapting their predictions based on the student's performance over time. This approach is more aligned with the continuous and iterative process of learning, acknowledging that a student's understanding of a concept can improve or deteriorate over time.

Knowledge Tracing Model(KTM) depicts an enhanced version of the knowledge tracing model, incorporating a "Tutor Intervention" element.

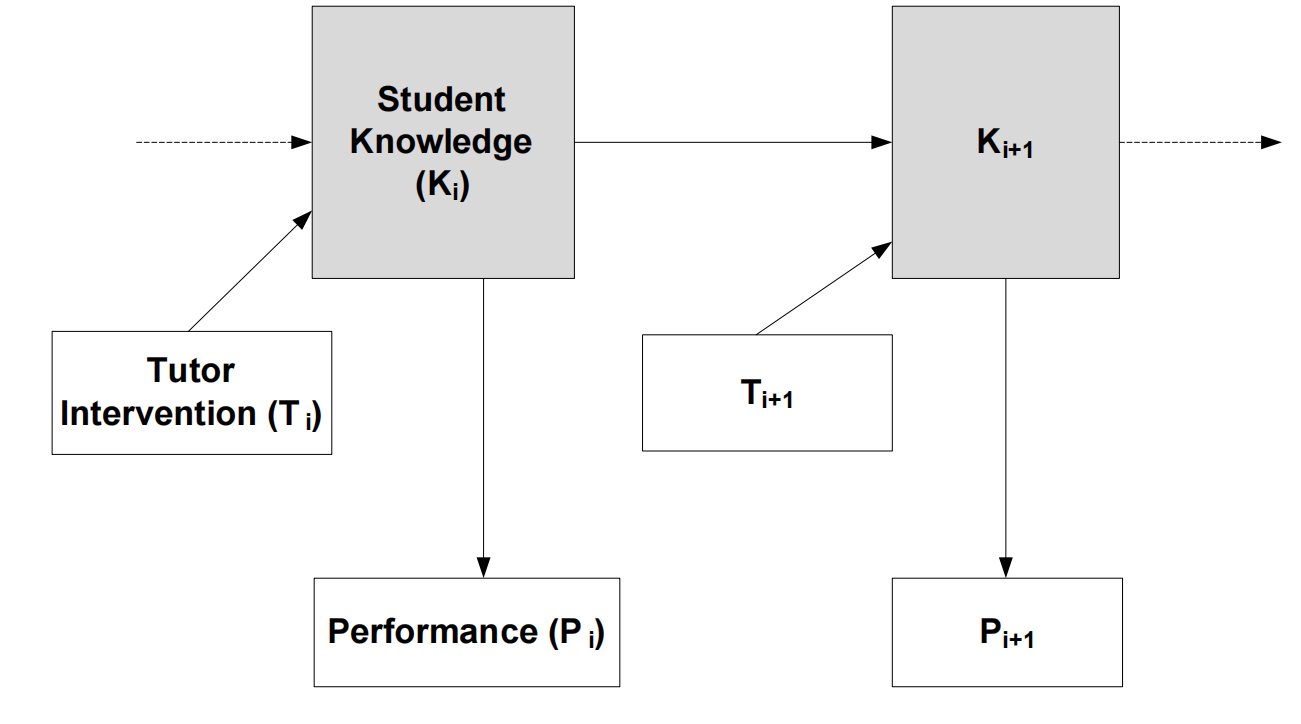
Figure 1: illustrates a dynamic Bayesian network (DBN) with three nodes at each time slice i. The hidden node K_i is a binary indicator of whether the student has mastered the skill by time i, with P_r(K_i) denoting the probability of this knowledge state. The observed node Pi captures the student's demonstrated ability on the skill at time i. DBNs expand the basic knowledge tracing framework by allowing for additional nodes; for example, Chang et al. included a node for help requests. In our model, we introduce a "Tutor Intervention" node T_i to represent the type of tutoring intervention provided at time i. The network's links represent the probabilistic dependencies between these factors.

The model parameters include:

knew: The likelihood that the student already understood the skill before instruction.

prob_Ti: The chance that the intervention applied is of a particular type i.

learn_Ti: The likelihood that a student learns the skill following an intervention of type T_i.

forget_Ti: The chance of forgetting a skill as a result of an intervention of type T_i.

guess: The probability of a correct answer even if the skill is not known.

slip: The probability of an incorrect answer despite knowing the skill.

Assessing the impact of various tutorial interventions boils down to comparing the "learn_Ti" and "forget_Ti" values for different interventions.

The model employs a two-stage implementation: an offline training process to derive parameters from historical performance data and a real-time updating mechanism to adjust the student's knowledge estimate after each observed performance. The BNT-SM knowledge tracing implementation uses an expectation-maximization (EM) algorithm for fitting and a Bayesian network inference process for updates.

Lastly, the representation of errors or discrepancies between what a student knows versus their performance is encapsulated in the noise dimension of student models. Models like KT acknowledge that students may guess a step correctly without knowing the underlying skill or slip at a step despite knowing the skill. This acknowledgment of noise is vital in creating a realistic and forgiving model that mirrors the imperfect nature of human learning and performance.

Each of these dimensions – temporal effect, skill dimensionality, credit assignment, higher-order effects, and noise – contributes to the complexity and efficacy of student models. “As we delve into these dimensions, we gain a deeper understanding of the intricacies involved in modeling student learning and the challenges in creating systems that can accurately predict and support a student's educational journey” [1]

2. Learning Decomposition in Educational Models

Learning decomposition, as a pivotal advancement in educational research, provides an in-depth analysis of different reading practices, such as massed versus distributed practice, and their impacts on reading fluency. This technique leverages fine-grained interaction data collected by computer tutors, applying it to understand various learning events and their relative impacts more intricately [2].

In the context of reading, learning decomposition aims to discern how different types of practice affect students' progress in reading skills. It offers a nuanced view, distinguishing between the effectiveness of massed versus distributed practice and wide versus re-reading. The study involves analyzing performance data on individual words, recorded over a school year, to examine how student progress in reading varies based on the type of practice.​​

The methodology of learning decomposition incorporates factors like student help speed and correctness into a single outcome measure. It emphasizes considering only the first encounter with a word on a particular day as a valid learning opportunity, thereby eliminating the effects of short-term memory retrieval on the demonstration of a student's knowledge.​​

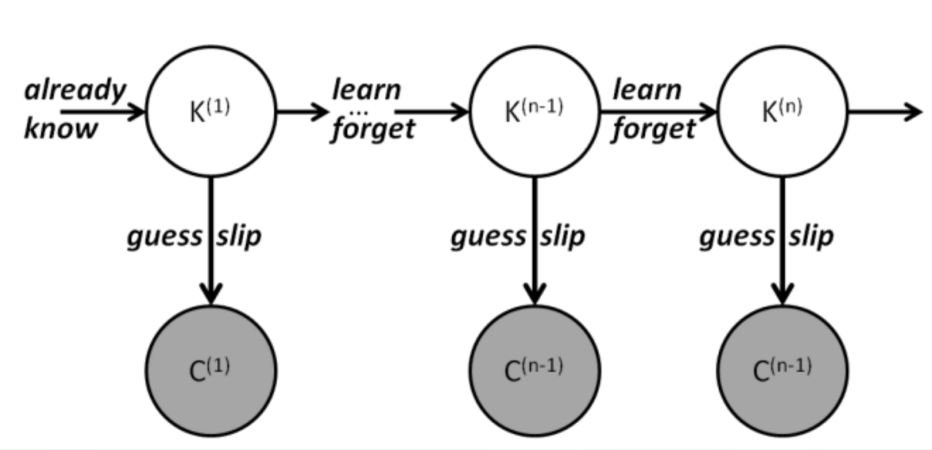
Figure 2: Single-skill knowledge tracing architecture

Figure 2 shows the graphical representation of the extended model. Student Knowledge (K_i) to K_i+1, Tutor Intervention (T_i) to T_i+1, Performance (Pi) to P_i+1. The figure shows that the model is a DBN with 3 nodes at each time step i. The binary-valued hidden node K_i represents whether the student knows the skill at time i. P_r(K_i) is a probabilistic estimate of this binary student knowledge variable. Pi represents the student’s observed performance (e.g., correct or incorrect) on that skill at the time i. Using a DBN for knowledge tracing allows us to expand its original formulation by including additional nodes. For instance, Chang et al. added a node to represent help requests​

Furthermore, the approach delves into the debate between wide reading versus re-reading. It differentiates encounters with new material versus rereading familiar stories, acknowledging that memorization can affect learning outcomes. This distinction is vital, as it influences the effectiveness of the reading practices being analyzed.​​

Findings from this approach reveal that rereading stories results in less learning than reading various stories. Additionally, mass practice or repeated exposure to a word within a short timeframe is generally ineffective, especially for proficient students.​​

The application of logistic regression in learning decomposition allows for classifying students based on the benefits they derive from different types of practice. This advancement enables the identification of student subgroups who benefit from specific practices, offering a more tailored approach to educational strategies.​​

3. Analyzing Tutoring Strategies through Models

Innovative approaches in educational research have revolutionized the evaluation of tutoring strategies. Notably, the Bayesian Evaluation and Assessment framework stands out for its dynamic and probabilistic approach to analyzing the efficacy of tutor assistance. This method differs significantly from traditional models by utilizing dynamic Bayesian networks, offering a fresh perspective on the impact of tutoring interventions [3].

The core principle of Bayesian Evaluation in Intelligent Tutoring Systems (ITS) is its ability to model tutor help and student knowledge in a unified framework. This approach allows for a nuanced examination of the effect of help, distinguishing between the immediate scaffolding of performance and the facilitation of long-term knowledge acquisition [3]. For instance, the tutoring system may provide help in various forms, such as sounding out a word or breaking it into syllables, each of which has different impacts on immediate performance and long-term learning [3].

Prior research using learning decomposition has shown the relative benefits of different learning encounters. Bayesian Evaluation builds upon this by comparing the value of tutor help against reading words without assistance. This comparison reveals the intrinsic worth of tutoring interventions in the learning process.

However, the learning decomposition model has found that reading a word is, by default, valued at 1.0 practice opportunities. In contrast, depending on the model used, help is estimated to be worth approximately -1.5 to -4 trials of learning, indicating that receiving help might cause students to perform worse in subsequent trials compared to situations where they did not receive help.

Addressing the shortcomings of previous approaches, Bayesian Evaluation focuses on controlling for the student’s knowledge of the skill being helped and refining the definition of what constitutes practical help. This is crucial as it accounts for both the immediate and long-term impacts of tutoring help on student performance.

The method unifies two common goals in Intelligent Tutoring Systems (ITS): assessing student knowledge and evaluating tutorial interventions. It does so by linking student performance with tutorial interventions so that both nodes are observable and their interactions are measurable. The approach assesses students as performance and knowledge are intertwined and evaluates tutorial intervention in terms of its temporary and lasting impacts on student knowledge.

The scaffolding effect on student performance can be estimated by comparing probabilities of correct responses under different intervention conditions. This allows for a clear delineation of how tutoring helps in immediate performance or long-term learning gains.

Bayesian Evaluation and Assessment (BNT-SM) allows for exploring different hypotheses on how knowledge is represented in student models. Despite its sophistication, this approach did not result in a more accurate assessment compared to simpler models like knowledge tracing.

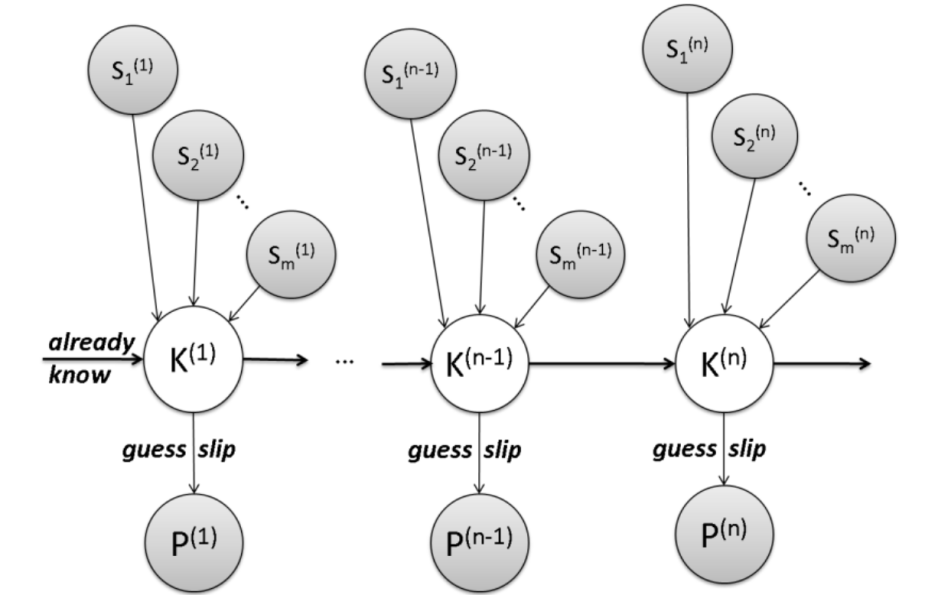
Figure 3: KT with Logistic regression

"LR-DBN is a recent but published method to trace multiple subskills, so we summarize it here only briefly in terms of the four aspects discussed in Section 2. Like standard KT, LR-DBN represents the knowledge for step n as a hidden knowledge state in a dynamic Bayes net. However, as Figure 3 illustrates, LR-DBN adds a layer of observable states as indicator variables to represent whether step n involves subskill j: 1 if so, 0 if not. LR-DBN uses logistic regression to model the initial hidden knowledge state and the transitions between states" [4]

4. Results

The studies' results in this paper highlight the nuanced implications these models hold for educational strategies, particularly in reading fluency [2]. The application of learning decomposition to a large dataset of student reading experiences revealed significant insights into the efficacy of various practice opportunities.

One of the main findings was the relative effectiveness of different reading practices. Rereading a story resulted in only 49% as much learning as reading a new story for the first time. This suggests that students learn to read words more effectively when exposed to a wide selection of stories rather than repeatedly reading the same story. Additionally, the analysis showed that massed practice, or multiple opportunities to practice a word on the same day, could have been more effective, especially for high-proficiency students. In fact, for these students, seeing the word again was almost a complete waste of time [2].

An essential contribution of this approach was the ability to detect student subgroups that benefit from specific types of practice. For instance, while rereading and massed practice was generally not beneficial, there were groups of students who did benefit from these practices. The analysis identified 11 students who helped from rereading and 5 who benefitted from massed practice, with learning support status and fluency being reliable predictors in the model. These findings suggest that while one-size-fits-all approaches might work for the majority, there are subgroups that require tailored approaches [2].

The equation 1 is an analysis framework for assessing the influence of student reading practice schedules and styles; it is a model of Analysis framework for evaluating the influence of reading practice schedules and styles.

\( Readingtime= l*word\_length+(w*wordID+A)*e-b*(r*m*RM+r*RD+m*NM+ND+h*\ \ \ helps) \) (1)

Word Length (l): the length of the word

Word Length * l: Longer words take more time to read.

Word Familiarity (w): Words that have been read before, either earlier that day or in the past, are read faster.

Proficiency (w∗wordID): More proficient readers can read faster.

First Trial Performance (A): How well students read on their first attempt affects subsequent readings.

Past Help (ℎ): How much help a student has received on a word influences how quickly they can read it.

The rest of the model uses learning decomposition to concurrently evaluate the effects of repetitive practice against spaced practice and comprehensive reading versus reviewing. The aim is to determine the optimal values for the r and m parameters to understand how different practice methods affect the advancement of student reading skills.

5. Conclusion and Future Directions

In conclusion, while the models discussed offer valuable insights, they also present limitations such as high standard errors, pointing towards areas for future research. These areas include the potential automation of decomposition analysis, which could enhance the precision and applicability of these models in educational settings. This direction suggests a focus on refining methodologies to overcome current challenges and improve the reliability of educational data analysis.

“Despite the significant contributions of the models discussed, they exhibit certain limitations, suggesting fruitful areas for future research. One notable limitation is the presence of high standard errors in learning decomposition, indicating a level of uncertainty in the model's parameter estimates” [5]. This uncertainty can affect the reliability of conclusions drawn from the data, underscoring the need for more robust methods in educational data analysis.

Another critical limitation is the potential for weak model fits in certain cases. For instance, while models like LR-DBN have shown promise in predicting and updating multiple subskills, they sometimes struggle to fit individual data points accurately. “This challenge highlights the complexity of modeling student learning and the need for more precise and accurate methods.” [6]

Future research in educational data mining focuses on automating learning decomposition to improve efficiency and accuracy. This involves integrating expert knowledge for valid outcomes and exploring different applications of concepts like massed practice for precise modeling. A proposed hybrid approach combines human expertise with computational power, aiming to enhance educational data mining and contribute to educational research effectively.