1. Introduction

In the realm of financial mathematics, option pricing theory serves as a cornerstone for understanding the valuation of derivative securities. The development and evolution of option pricing models offers mathematical tools to value financial derivatives with efficiency and accuracy. The study of option theory begins with Black-Scholes model. This ground -breaking innovation provided a theoretical framework for pricing Europe options on non-dividend-paying stocks based on partial differential equations and stochastic calculus. The significance of the Black-Scholes model lies not only in its function to set the price of an option based on certain assumptions but also in its influence on the history and development of option pricing model. It established a foundational approach for further research and addressed the complexities of financial markets [1].

During the years following the introduction of Black-Scholes model, the landscape of option pricing theory has witnessed sustainable growth and diversification. Researchers and practitioners have been seeking to break through the deflects of the Black-Scholes model, from the assumptions of constant volatility and interest rates to its inability to price American options accurately. This pursuit has led to the emergence of numerous models aiming to reflect market conditions as well as the behaviors of financial instruments more precisely [2]. Among them, the Black-Scholes-Merton model extension for dividend-paying market for dividend-paying stocks, the Cox-Ross-Robinstein binomial tree model and the Heston model featuring its stochastic volatility framework, stand out for their contributions to this realm. Today, the exploration of option pricing theory continues to evolve, with research hunting through areas like machine learning algorithms for pricing and the impacts of macroeconomics factors on option valuation [3].

The essay is organized to present a comprehensive overview of the evolution of option pricing models. The first section is about the foundations, limitations, and extension of Black-Scholes model. The subsequent section then transitions to the Heston model, underscoring the innovative approach to modeling stochastic volatility. The final section examines the cutting-edge research and emerging trends in the field.

2. Black-Scholes Model:

2.1. Foundations of the Black-Scholes Model

Geometric Brownian motion, the theoretical foundation of the Black-Scholes model, elucidates the randomness of the price of the underlying asset. Mathematically, this is expressed by the following equation [4]

\( \frac{dS}{S}=μdt+σdW\ \ \ (1) \)

Here, \( S \) represents the price of the underlying asset, \( μ \) is the expected return or drift, \( σ \) is the volatility of the asset’s returns, \( dt \) denotes the change in time, and \( dW \) represents a Wiener process, which captures the random fluctuations in the asset’s price.

The Black-Scholes model makes several key assumptions. The first is the constant volatility. The volatility of the underlying asset’s returns remains constant over the option’s lifetime. The second is continuous trading. Investors can buy and sell the underlying asset continuously without transaction costs or market frictions. The third is no dividends. The underlying asset pays no dividends during the option’s lifetime. Finally, it is about the risk-free interest rates, meaning that investors can borrow and lend money at a risk-free rate. Based on these assumptions, the Black-Scholes formula provides a closed-form solution for pricing European call and put options. The Black-Scholes formula furnishes a closed-form answer for the pricing of European call and put options, based on these suppositions [5]

\( C={S_{0}}N({d_{1}})-K{e^{-rt}}N({d_{2}})\ \ \ (2) \)

and

\( P=K{e^{-rt}}N(-{d_{2}})-{S_{0}}N(-{d_{1}}).\ \ \ (3) \)

Likely, \( C \) and \( P \) represent the prices of the call and put options, respectively. \( {S_{0}} \) is the current price of the underlying asset, \( K \) is the strike price, \( r \) is the risk-free interest rate, \( t \) is the time to expiration, and \( N \) is the cumulative standard normal distribution function. In addition, \( {d_{1}} \) and \( {d_{2}} \) are calculated as follows

\( {d_{1}}=\frac{ln({S_{0}}/K)+(r+{σ^{2}}/2)t}{σ\sqrt[]{t}}\ \ \ (4) \)

and

\( {d_{2}}={d_{1}}-σ\sqrt[]{t}.\ \ \ (5) \)

The Black-Scholes equation delineates the correlation between the price of options and multiple factors and offered clarity on the dynamics of option pricing. To be more precise, it explicates how variations in these factors influence the valuation of options and elucidates the emergence of the volatility smile phenomenon.

2.2. Challenges and Limitations of the Black-Scholes Model

Despite the significant influence of the Black-Scholes model in financial mathematics, it encounters imminent challenges. A primary issue is its presumption. The assumption of constant volatility, mathematically represented by a specific parameter in the Black-Scholes formula, does not align with reality. In fact, volatility shows time-varying behavior, or stochastic volatility, leading to discrepancies in option pricing by the Black-Scholes model, especially during times of market uncertainty [6].

Another shortcoming also lies in the assumption. The model overlooks market frictions and transaction costs. In practical markets, however, investors incur trading costs, including bid-ask spreads, brokerage fees, and market impact, all of which influence option prices and trading strategies. The Black-Scholes model presumes a market without frictions, thus causing potential variances between theoretical and actual option prices [7].

Moreover, the model is tailored for European-style options, exercisable only at expiration. So, obviously it falls short for American-style options, which permit exercise at any point before expiration. Although there are methods to estimate American option prices using the Black-Scholes framework, these approaches may introduce further complexities and uncertainties.

As people all know, in 1970s, Black and Scholes suffered serious financial losses and were once out of the Wall Street. This dismayed experience underscores the model’s inherent flaws. Addressing these challenges is crucial for devising more precise and reliable option pricing models in the future.

2.3. Extensions to the Black-Scholes-Merton Model

The Black-Scholes-Merton model is an extension of the original Black-Scholes model, incorporating the payment of dividends on the underlying asset. Mathematically, in order to extend the Black-Scholes model to account for dividends, the concept of dividend yield, denoted by q, is introduced, which represents the continuous dividend payment per share per year, expressed as a percentage of the stock price. The adjustment to the Black-Scholes formula involves subtracting the present value of dividends from the current stock price. In other word, \( {S_{0}} \) is modified to \( {S_{0}}-PV(D) \) , where \( PV(D) \) represents the present value of dividends. Thus, the Black-Scholes-Merton model for a European call option becomes [8]

\( C=({S_{0}}-PV(D))N({d_{1}})-K{e^{-rt}}N({d_{2}})\ \ \ (6) \)

and

\( PV(D)=D{e^{-qt}},\ \ \ (7) \)

where \( D \) is the dividend payment per share, \( q \) is the dividend yield, and \( T \) is the time for expiration.

3. The Emergence of Stochastic Volatility Models

Stochastic volatility models have significantly advanced option pricing theory. So what’s the differences? The differences new models made are changing the Black-Scholes assumption of constant volatility. By incorporating variability into the volatility process, these models offer a more nuanced depiction of market behaviors, thereby enhancing the accuracy of option pricing.

A landmark development in stochastic volatility modeling is the introduction of the Heston model by Steven Heston in 1993. This model enhances the Black-Scholes framework through the integration of a stochastic process for volatility, making it a more dynamic and realistic approach to modeling market conditions. The underlying dynamics of the Heston model are described by a set of stochastic differential equations, which jointly model the price of the underlying asset and its volatility. This is a dual process framework. It allows for the volatility to change over time, reflecting the actual conditions observed in financial markets more closely.

\( d{S_{t}}=r{S_{t}}dt+\sqrt[]{{v_{t}}}{S_{t}}dW_{t}^{1}\ \ \ (8) \)

and

\( d{v_{t}}=κ(θ-{v_{t}})dt+σ\sqrt[]{{v_{t}}}dW_{t}^{2}\ \ \ (9) \)

Here, \( {S_{t}} \) is the asset price, \( {v_{t}} \) is the instantaneous variance, \( r \) is the risk-free rate, \( κ \) is the mean-reversion rate, \( θ \) is the long-term average volatility, \( σ \) is the volatility of volatility, or ‘vol of vol’, and \( W_{t}^{1} and W_{t}^{2} \) are Weiner processes. As can be seen from the equations above, the Heston model permits volatility to fluctuate overtime, providing more accurate pricing for options, especially in volatile market [9].

Beyond the Heston model, the field of stochastic volatility modeling has expanded to include various other models, each with unique features catering to specific aspects of financial markets. The SABR (Stochastic Alpha, Beta, Rho) model, introduced by Hagan and colleagues in 2002, stands out for its application in the interest rate derivatives markets. The SABR model is particularly noted for its ability to accurately model the ‘volatility smile’. It is called ‘smile’ because, as one can see in the Figure 1 below, the both sides of the function curve is high while the middle part is low. The Black-Scholes model cannot adequately capture it. This capability makes the SABR model highly effective for calibrating to market data, thereby providing an efficient tool for pricing and risk management in complex financial markets.

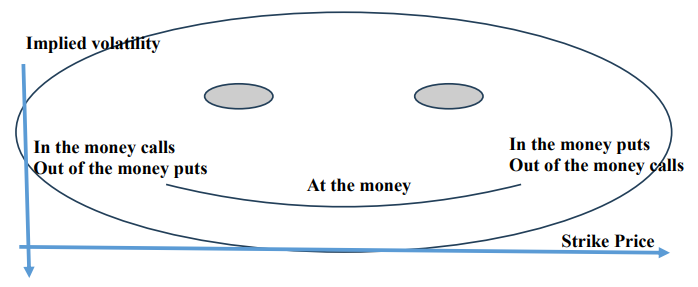
Figure 1. Relation between strike price and implied volatility.

Another notable stochastic volatility model is the Bates model, proposed by David Bates in 1996. The Bates model incorporates jumps in asset prices and stochastic volatility, providing a more comprehensive representation of market dynamics. This model applies to pricing options on assets with significant discontinuities, such as commodities and equity indices. Mathematically, stochastic volatility models introduce additional complexity compared to the Black-Scholes model and thus offer significant advantages in option pricing accuracy, especially in volatile markets. While newer models like the SABR and Bates models apply to various financial market, the Heston model remains influential.

3.1. Applications and advantages of Heston model

The Heston model offers several advantages over traditional option pricing models and has diverse applications in finance, since its mathematical formulation and flexibility make it a valuable tool for understanding and pricing derivative securities in various market conditions. So why the Heston model is ‘better’ than the Black-Scholes-Merton model? The main advantage of the Heston model, compared to the original Black-Scholes-Merton model, is its ability to capture the dynamics of both asset prices and volatility simultaneously by incorporating stochastic volatility, which allows the model to reflect the observed volatility clustering and mean-reverting behavior in financial markets more accurately [10].

Another advantage is that the Heston model can capture volatility smile phenomenon, which implies option traders are willing to pay more for options that are in or out of the money than for options that are at the money, while the Black-Scholes-Merton model fails to capture the phenomenon. Thus, the Heston model has diverse applications in finance besides option pricing. The first is Risk Management. The Heston model provides insights into the risk exposure of derivative portfolios by allowing traders and risk managers to assess the impact of changes in market conditions on option prices and implied volatilities. This information is crucial for hedging strategies and risk mitigation in contrast with Black-Scholes model. In fact, Black and Scholes lost millions of dollars due to lack of risk management. The second is Volatility Trading. The Heston model can be used to develop trading strategies based on forecasts of future volatility. Finally, it is about Derivatives Valuation. Beyond options, the Heston model can be applied to other derivative securities as well, such as variance swaps and options on variance, where stochastic volatility plays a significant role in pricing.

3.2. Beyond Heston: Recent Advances in Option Pricing

The evolution of financial modeling, particularly in option pricing, has been marked by significant advancements that extend beyond the pioneering efforts of the Heston model. These recent developments have been instrumental in addressing the multifaceted nature of financial markets today, providing enhanced precision, adaptability, and insights. Here’s an overview of some.

What comes first is rough volatility models. Recent years have seen the introduction of rough volatility models, which represent a paradigm shift from the conventional geometric Brownian motion assumption to embracing fractional Brownian motion or other processes that exhibit rough behavior. This approach has proven effective in capturing the intricate details of volatility surfaces, offering a more accurate depiction of market realities. Rough volatility models are particularly adept at reflecting the genuine complexity and unpredictability of market volatility, addressing some of the key limitations inherent in traditional stochastic volatility models. Another notable advancement is the application of machine learning techniques. The integration of machine learning (ML) into option pricing signifies a substantial leap forward. Techniques such as neural networks and deep learning are now being employed to navigate the complex dynamics of financial markets. Unlike traditional parametric models, ML models excel at recognizing nonlinear relationships and managing high-dimensional datasets. These algorithms are capable of learning from vast amounts of historical market data and dynamically adjusting to new market conditions, offering a potent tool for real-time financial analysis and decision-making.

Advancements in computational finance also make great contributions. The development of sophisticated numerical methods has greatly enhanced the ability to solve complex option pricing models. Innovations in Monte Carlo simulations, finite difference methods, and tree-based approaches have expanded the toolkit available for tackling the increased sophistication of contemporary financial models. These advancements not only facilitate the handling of models with greater complexity but also improve the efficiency and accuracy of option pricing calculations. Together, these advancements represent a significant evolution in the field of financial modeling, offering a deeper understanding of market dynamics and providing financial professionals with more robust tools for option pricing and risk management. By leveraging these innovative approaches, the finance industry is better equipped to navigate the intricacies of modern markets and make more informed decisions based on sophisticated analyses. The relationship among different models are shown in Figure 2.

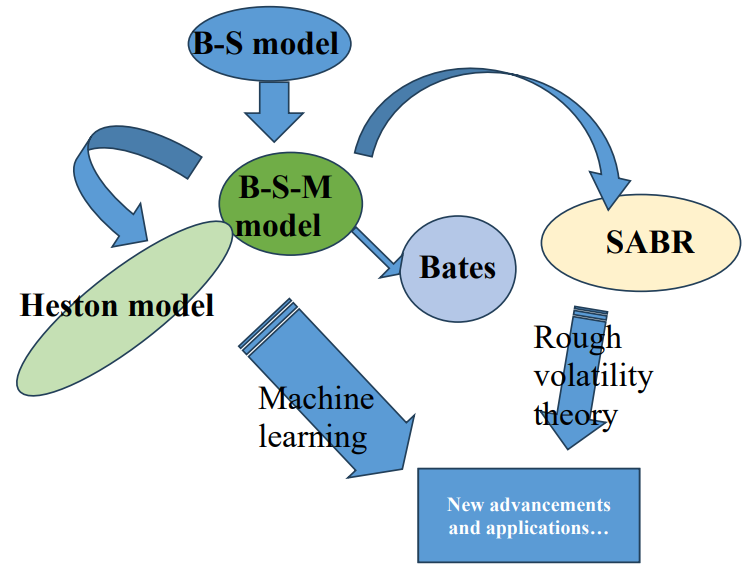
Figure 2. Relation Among different models.

4. Conclusion

The evolution of option pricing models from the Black-Scholes framework to sophisticated stochastic volatility models like the Heston model reflects the continuous efforts to enhance people’s understanding and capabilities in financial mathematics. The author has explored the foundational principles of option pricing theory, delving into historical developments, key concepts, and significant models that have shaped the field. Simple and elegant as the Black-Scholes-Merton model is, it has limitations that spurred the development of more advanced models. The introduction of stochastic volatility models, exemplified by the Heston model, has significantly improved option pricing accuracy by capturing the dynamics of volatility, which turns out to be a crucial factor in financial markets. Beyond the Heston model, recent advances in option pricing, such as rough volatility models and machine learning techniques, offer promising avenues for further research and innovation. These developments address the complexities of modern financial markets and provide new insights into option pricing dynamics.

Looking ahead, future research in option pricing theory is likely to focus on several key areas. Refining existing models and developing more accurate representations of market dynamics will remain a priority. Additionally, new tools like deep learning and quantum computing could yield novel insights and methodologies for option pricing. Furthermore, the application of option pricing models in practical settings, such as risk management, derivative valuation, and trading strategies, will continue to drive research efforts. Understanding the implications of option pricing models in real-world scenarios and adapting them to changing market conditions will be essential for their broader adoption and effectiveness. In conclusion, the journey from the Black-Scholes model to advanced stochastic volatility models represents a continuous quest for precision and innovation in option pricing theory. By building on the foundations laid by pioneering researchers and embracing new technologies and methodologies, the future of option pricing holds exciting possibilities for further advancements in financial mathematics and its applications in modern finance.