1. Introduction

In Quantum Gluon-Plasma (QGP) experiments, two heavy particles are accelerated to high energy and collided to break the bond of nucleons in each particle, which then leads to a brief QGP state. In common QGP experiments, some simple configurations, the number of participated nucleons, for instance, can be measured. However, some geometrical structure such as the impact parameter and shape of collision regions are hard to determine directly from experiments [1]. Nevertheless, it is possible to predict these geometric configurations using the percentile centrality of a collision with Glauber models of contents of a typical nucleus [2]. These models, with a recent review [3], are divided into two classes. The \optical" Glauber calculations assume a smooth matter density and are described by a Fermi Distribution in radial direction and uniform over solid angle. The other type of model, Monte Carlo based models, assumes the stochastic nature of event-by-event individual nucleon distribution, and allows the collision properties to be determined by averaging over multiple events. From [3]and [4], it could be found that both models produce similar results for simple quantities, such as the number of participation nucleons ( \( {N_{part}} \) ), and impact parameters ( \( b \) ).

Furthermore, Recent research also demonstrated that despite the traditional impression that most participating particles collided in the elliptical region with eccentricities 2, there are also triangular regions with triangularity3 produced in heavy ion collisions [3].

In this paper, methods of PHOBOS Monte Carlo based Glauber Model (MC Glauber) like [5] are employed to simulate collisions of particles. In The Model section, assumptions for building up the model are introduced. In The Study of Participating Area section, the model is implemented to obtain the correlation between \( {N_{part}} \) , and \( {ε_{2}},{ε_{3}} \) .

2. The Model

The analysis process is a three-step method. Firstly, set up the nucleon positions in each nucleus, and make sure each nucleon's position is stochastically determined. Then assuming the straight-line collision and let two particles “collide" each other along the beam axis, so that we can tag nucleons as participating or spectating the collisions. Thirdly, repeat the collision event and obtain more data, then do the statistics to obtain correlations between \( {N_{part}} \) , and \( {ε_{2}},{ε_{3}} \) .

2.1. Nuclei Make Up

With reference to [2]and [6], the nucleons are uniformly distributed within the sphere, where the randomness distribution follows the Wood-Saxon distribution as shown below.

\( ρ(r)=\frac{1+w{(\frac{r}{R})^{2}}}{1+exp{(\frac{{r^{2}}-{R^{2}}}{{a^{2}}})}} \)

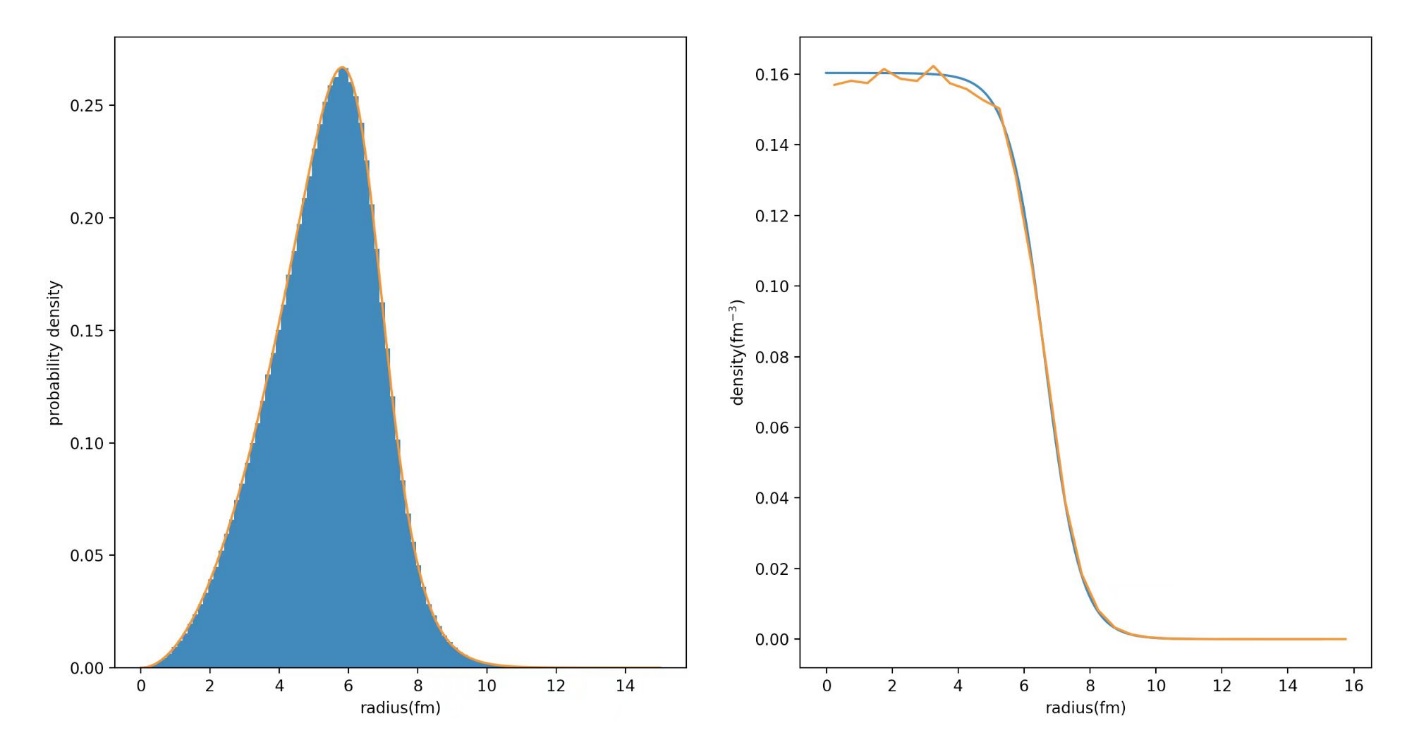
The data of nucleons generated are collected and compared with theoretical distribution, as shown in fig.1. Also, the result is consistent with figure 1 in [7], another model constructed by other researchers.

2.2. Collision Process

The collision is assumed as inelastic, and the randomly chosen impact parameter is capped at a maximum of \( {b_{max}}≈20fm \gt 2{R_{A}} \) [5]. The center of each nucleus is therefore shifted \( (±\frac{b}{2},0,0) \) .

The diameter for the cross-section is also called the \ball diameter", which is given by equation (4) in [5] as

\( D=\sqrt[]{\frac{{σ_{NN}}}{π}},whereatLHC{σ_{NN}}≈72mb \)

The collision of nucleons from two different nuclei is determined by their relative transverse distance. If the distance between two nucleons is smaller than the ball diameter, the collision will be thought as occurred and these two nucleons will therefore be marked as collided. The figure 2 demonstrates an illustration of one collision event:

2.3. Eccentricity \( {(ε_{2}}) \) and Triangularity \( ({ε_{3}}) \) Calculation

The calculation of \( {ε_{2}},{ε_{3}} \) employed the following formula from [5]:

\( {ϵ_{2}}=\frac{\sqrt[]{{({r^{2}}cos{(2{ϕ_{part}})})^{2}}+{({r^{2}}sin{(2{ϕ_{part}})})^{2}}}}{{r^{2}}} \)

\( {ϵ_{3}}=\frac{\sqrt[]{{({r^{2}}cos{(3{ϕ_{part}})})^{2}}+{({r^{2}}sin{(3{ϕ_{part}})})^{2}}}}{{r^{2}}} \)

where \( r,{ϕ_{part}} \) denotes the location of participated nucleon in center of mass reference frame.

2.4. Comparison with Previous Model

The figure 3 shows the histogram of \( {N_{part}} \) and number of collisions, \( {N_{coll}} \) , and it complies with the result from figure 8 in [8]:

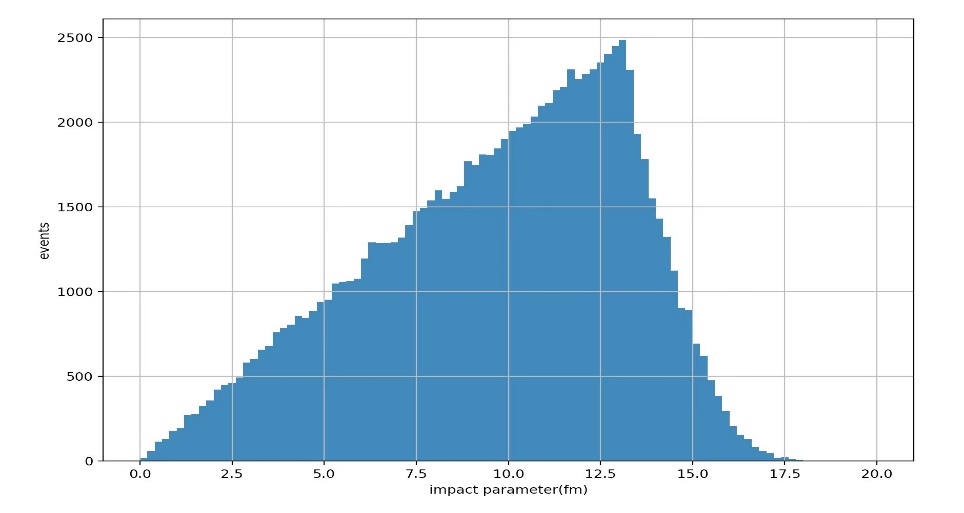
Figure 4 demonstrates the histogram of impact parameter versus \( \frac{dN}{db} \) . It could be noticed that the shape of the graph is linear when the impact parameter is less than certain value ( \( ∼14fm \) ), and after that there's a quick drop. That means when impact parameter is greater than \( 14fm \) , the collisions are less likely to happen.

3. The Study of Participating Area

3.1. Eccentricity ( \( {ϵ_{2}}) \) of the Collision Region

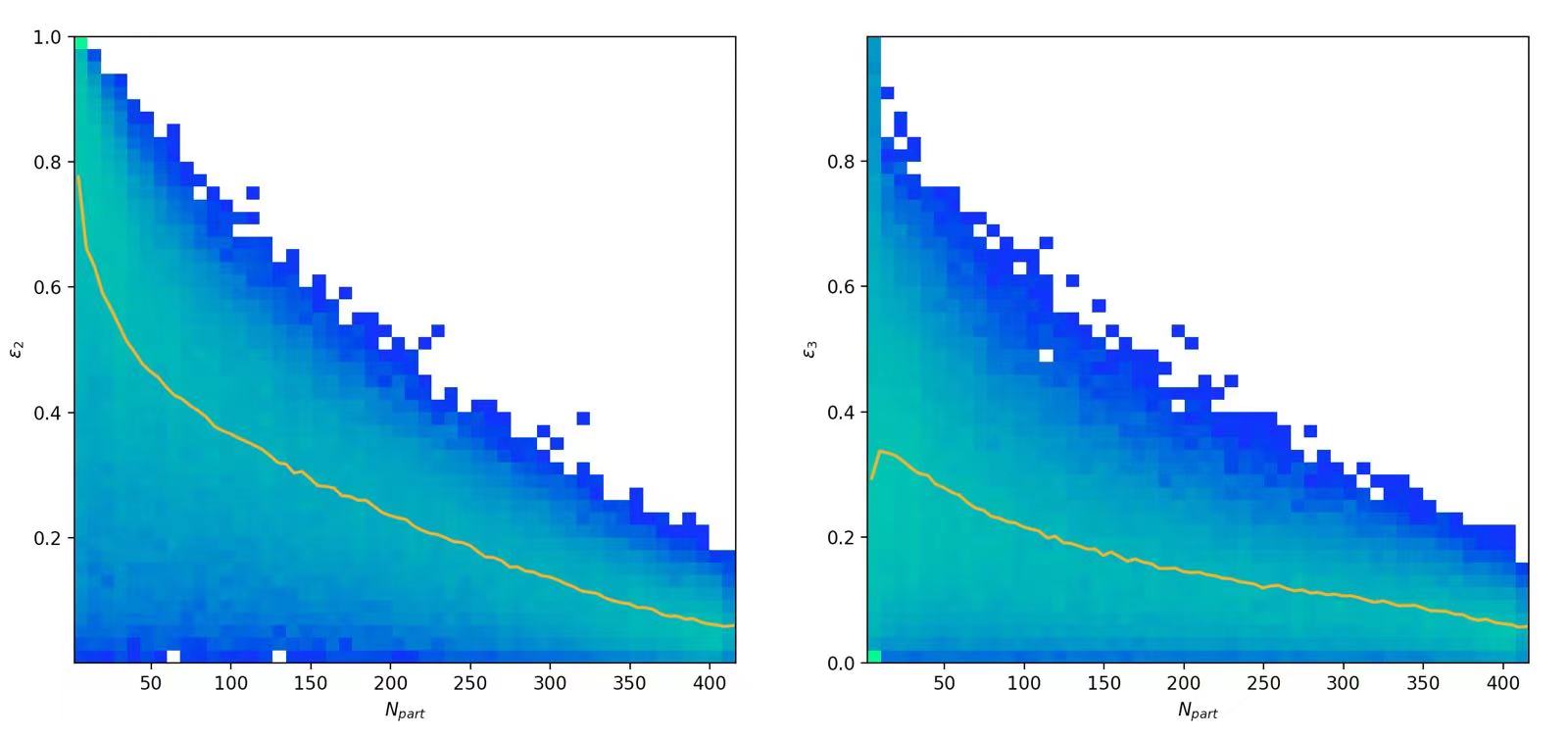
The left side of figure 5 This result agrees with the study of [2]. It presents that the less nucleon participated in collision, the more likely that shape will be an ellipse. This is easy to understand, as the less participants, the more participants will cluster at the foci of the ellipse, and hence make the shape more likely to be an ellipse. In quantum view, it could be understood as the fact that the elliptical shape is influence by both the fluctuation of the nucleons as well as the shape of the intersecting area [2], [5].

3.2. Triangularity ( \( {ϵ_{3}}) \) of the Collision Region

Notice that in figure 5, when only few nucleons participated in the collision, triangularity is significantly less than the value of eccentricity. This is because \( {ϵ_{3}} \) is only influenced by fluctuation, whereas the \( {ϵ_{2}} \) is influenced by both fluctuation of nucleons and the shape of intersection.

Also, the fast decrease of \( {ϵ_{3}} \) is demonstrated. Due to the increasing number of particles, fluctuation of nucleons in collision is significantly decreased, and hence the \( {ϵ_{3}} \) decreases.

3.3. General Analysis of \( {ϵ_{2}}{,ϵ_{3}} \)

Notice that in figure 5 both \( {ϵ_{2}} \) and \( {ϵ_{3}} \) reaches similar values when \( {N_{part}} \) reaches maximum. This happens as the influence of both fluctuation and shape of intersection is at minimum at this point. The impact of fluctuation is illustrated in section above. The intersecting shape tends to be similar when every nucleon participates in, and hence also has little impact on the elliptical shape.

4. Conclusion

This paper displayed the simulation of the collision of heavy nuclei with the application of the Glauber model based on Monte Carlo, and the geometry of eccentricity and triangularity of the colliding region is studied. The correlation between the shape of region and $N_{part}$ is found: the more nucleons participate in collision, the less likely that the colliding region will have elliptical or triangular shape.

This model does not ignore overlapping nucleons when generating nuclei, hence may have some random errors. However, this randomness should be eliminated by repeating collision simulation for tremendous number of events.

The limitation of randomness (numpy.rand) used in python coding may cause some systematic error to the model, but it shall not influence the result a lot.