1.Introduction

The increasing population and apparent climate change have exacerbated the issue of insufficient resources on Earth to sustain basic living conditions. In terms of this problem, scientists tend to discover a plan for moving human beings to other livable planets, such as Kepler-22b which is regarded as the most famous livable planet in the universe that scientists have discovered. However, the significant distance from Earth necessitates an extensive travel time for a spacecraft to reach this destination, which could have detrimental effects on human health and well-being. Prolonged exposure to the harsh conditions of space can result in increased radiation exposure, detrimental to human physiology, as well as muscle atrophy. This research aims to gather fundamental information about Kepler-22b, explore relevant concepts and methodologies, outline essential conditions for travel, and identify the limitations encountered in efforts to shorten the time required for travel to Kepler-22b. Such investigations not only enhance the application of the time dilation method but also contribute to addressing the broader challenges of interplanetary travel, whether from Earth to Kepler-22b or to other celestial bodies. Ultimately, this research assesses the acceleration that individuals have to experience and time difference, which also can be regarded as the proportion of the time taken on the space ship in terms of Earth, thereby supporting the theoretical foundation required for achieving interplanetary travelling.

2.Methodology

2.1.Kepler-22b

Kepler-22b is a planet from Cygnus, approximately 638 light-years away from Earth. It was first discovered in 2009 by the Kepler telescope. In addition, it was the primary planet that human beings have found in the habitable zone in the universe, with the potential to contain liquid water on its surface. Moreover, scientists infer that Kepler-22b may possess temperatures comparable to those on Earth, making it a potentially suitable environment for human habitation.

2.2.Concepts

This research contains the concept of time dilation, twins and time travel, acceleration motion, constant proper acceleration, etc.

Gamma: This research uses the formula of r=1/math.sqrt 1-v**2/c**2 to calculate the number of gamma(1<r<30) in different velocity of the spaceship. According to the function graph illustrated below. It is apparent that when the velocity is approximate to the light speed, the number will be closer to 30, which means the scale effect will be more obvious. To be specific, the graph contains an asymptote, signifying that the gamma factor increases dramatically as the velocity approaches the speed of light.

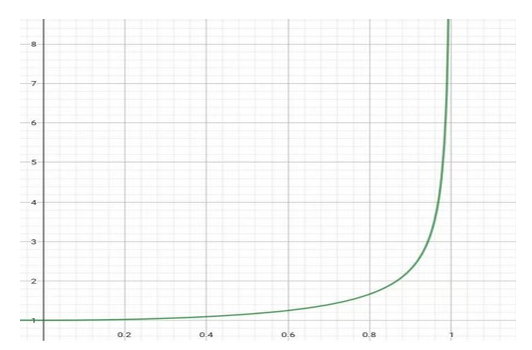
Figure 1: The function of gamma related to the light speed.

x-axis is the percentage of the object’s velocity in terms of the light speed

y-axis is the number of gamma

Time taken: In case of the increase in the number of gamma, the time taken will also be different based on the formula 1/v=1/vr, in which the line graph best illustrates the discrepancy, the space between the green and blue lines, of the time use.

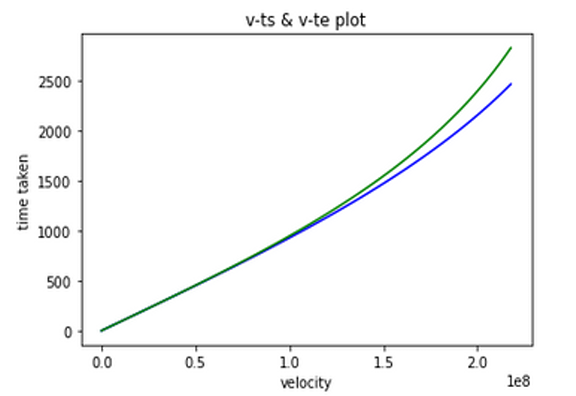
Figure 2: The time in the spaceship and the time in the Earth in the same distance.

1/math.sqrt(1-v**2/c**2)

This is the formula for how to calculate the gamma, which is related to the velocity of the object and the light speed, 3.0e8.

2*c*l/v*(1+2*p/l*(1-1/r))/c

((2*c*l/r)/v*(1+(2*p/l)*(1-r))+4*p*math.asinh(v*r/c))/c

(2*c*l/v*(1+4*p/l)*(1-1/r)-4*p*math.asinh(v*r/c))/c

2.3.Planetary Travelling

Twins revisited

The graph shown below presents the distance and the velocity of an object traveling between planets. The object first accelerates from X₀ to X to a great speed, then uses constant velocity to travel consistently at X₁ to X₂. Eventually, it deaccelerates and lands on the surface of the destination. The rest of the graph mirrors the initial process, depicting the return journey back to the point of origin.

Based on this diagram and using Python, this research developed a program that calculates the time elapsed on Earth and the destination planet.

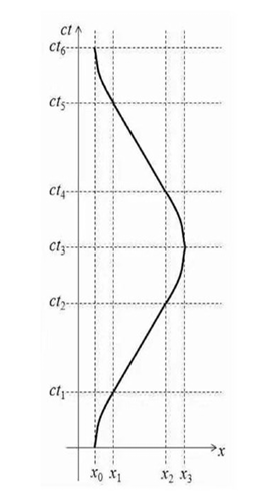
Figure 3: The function of the velocity and the displacement of the spaceship during the interplanetary travelling

This program is used to generate a graph that visualizes the extent of time dilation occurring throughout the travel process.

import math

import matplotlib.pyplot as plt

# Enter the velocity and number of point

v = float(input("Enter the initial velocity: "))

vf = float(input("Enter the final velocity: "))

npoints = int(input("Enter the number of points: "))

# create empty list for the velocity and gamma data

l=6.0359e15

v_data=[]

t_data=[]

gamma=1/math.sqrt(1-v**2/c**2)

increment = vf/npoints

for i in range(0,npoints):

gamma=1/math.sqrt(1-v**2/c**2)

t=l/v*gamma

v = v + increment

v_data.append(v)

t_data.append(t)

plt.plot(v_data,t_data,"m")

plt.title("time to kepler 22b")

plt.xlabel("v")

plt.ylabel("t")

This program is responsible for calculating the time between the Earth and the spaceship under specific acceleration and constant distance conditions.

import math

a0 = float (input ("Enter the acceleration of the object:"))

v = float (input ("Enter the velocity of the object:"))

l = float (input ("Enter the distance:"))

c = 3.0e8

p = c**2/a0

r = 1/math.sqrt(1-v**2/c**2)

te = 2*c*l/v*(1+2*p/l*(1-1/r))/c

ts = ((2*c*l/r)/v*(1+(2*p/l)*(1-r))+4*p*math.asinh(v*r/c))/c

td = (2*c*l/v*(1+4*p/l)*(1-1/r)-4*p*math.asinh(v*r/c))/c

dt = te-ts

print ("The time taken on earth is ", str(te))

print ("The time taken on the spaceship is ", str(ts))

print ("The difference in time is ", str(dt))

print ("The time diff is ", str(td))

This research assumed that the acceleration of the object (a0) is a range from 45 to 900, representing the maximum gravitational field that humans could endure over the long term and the extreme gravitational force that humans can tolerate, respectively. In addition, the investigation supposes that there is enough energy and advanced technology to support to velocity of the spaceship to reach the speed up to 2.9e8. Ultimately, the distance is constant which is 6.0359e15 km between the planets. Thus, the only variable that can be manipulated is the acceleration of the spaceship to minimize harm to the human body.

3.Results and Analysis

Table 1: The constant data to calculate the percentage

Table 1 presents the conditions controlled and manipulated in this study, and the constant data that the research used to calculate the percentage.

4.Conclusion

This research uses Jupiter software and the Python programming language to calculate data and results. According to the chart, it is apparent that a value can be found that optimizes time reduction while minimizing the required acceleration. It is estimated that at an acceleration of around 200, the time spent in space can be reduced by approximately 40%. This reduction in time exposure to harmful radiation and acceleration would significantly mitigate the challenges faced during space travel. However, this acceleration seems too large to be accepted, there are some methods such as “spring beds” which can help human beings feel better.

To travel at higher speeds and sustain greater acceleration, the energy required for the spaceship would increase significantly. Current technology is insufficient to meet these demands, necessitating the development of new and reliable methods to achieve this goal.

In terms of acceleration, it is known that any acceleration greater than 4.5 times Earth’s gravity can negatively impact human health. However, the chart illustrates that the gravity should be approximately 200 to achieve a noticeable time discrepancy. Thus, new innovations are needed to mitigate the adverse effects of such high acceleration on the human body