1. Introduction

In the digital era aiming to simplify the communications among users of electronic devices, the penetration rate of heterogeneous network has witnessed a dramatic increase in the past decades [1]. Correspondingly, due to the constructive demand of security and privacy maintenance amid the public internet users, in 1985 Neal Koblitz and Victor Miller independently developed a brand new public key cryptosystem named Elliptic Curve Cryptography (ECC), which is the most typical algorithm allowing the complexity of ECDLP to guarantee the high information security [1-3]. Since the complicated cryptosystem involves a wide range of functions including error detection, image decode, small grid establishment and so on [3-5], the sophisticated ECC algorithm is consisted of divergent principles worth further explorations and illustrations.

As a result, the Elliptic Curve Cryptography is applied in both software and hardware, which has successfully overcome the shortcoming in current cryptographic methods revealed by Mathematical cryptanalysis [3], will be the topic on which this paper consistently focuses to generally analyze its fundamental principles beneficial for a better understanding about the foundation of ECC. Based on the relevance sequence, the main body of the article will be divided into four sections: (1) the elliptic curve cryptography, in which the origin and definition of ECC will be identified; (2) the law of addition, which is different from the calculation law of Euclidean space; (3) ECDLP, a Mathematical problem widely regarded as the security root of ECC encryption [3]; and (4) EC ElGamal, a typical transplant of the elliptic curves practically used in modern cryptosystem.

After a comprehensive illustration using qualitative research and exemplary analysis, the research will possibly assist the readers in better understanding Mathematical principles of the Elliptic Curve Cryptography, and stimulate the further development of ECC to obtain a more reliable cryptosystem by which the network communications through plaintext and ciphertext will become by far safer.

2. Elliptic curve cryptography

ECC, an algorithm based on elliptic curve mathematics for establishing public-key cryptography, entered wide use from 2004 to 2005 after it had been initially proposed by Neal and Victor in 1985 [6].

2.1. Elliptic curve origination

Elliptic curve, which dominates no physical resemblance with an ellipse, is a descendant term originating from the close association with the cubic algebra elliptic equation describing the perimeter of an ellipse [7]. In detail, the perimeter formula of an ellipse can be written in the form below:

\( L=4a\int _{0}^{\frac{π}{2}}\sqrt[]{1-{e^{2}}{sin^{2}}{θ}}dθ=4aE(e,\frac{π}{2}) \) (1)

the polynomial \( E(e,\frac{π}{2}) \) is named the Second Complete Elliptic Integral, guaranteeing the existence of an equation in the form of \( {y^{2}}+aty+by={t^{3}}+c{t^{2}}+dt+e \) , which satisfies:

\( f(x)=\int _{c}^{x}R|t,\sqrt[]{{t^{3}}+c{t^{2}}+dt+e}|dt \) (2)

Therefore, the common elliptic curve used in cryptography is witnessed: \( {y^{2}}={x^{3}}+Ax+B \) , which vividly elucidates the reasons for the name “Elliptic Curve” [8].

2.2. Elliptic curve in cryptography

As the article mentioned before, the Elliptic Curves Cryptography uses the curve equations in the form of \( {y^{2}}={x^{3}}+Ax+B \) (A, B are the constant) most frequently, which is known as Weierstrass equation where the elliptic curve is required to be non-singular (i.e., no tip, no self-intersection, no isolated point) [2]. Thus, this condition is equivalent to [1]:

\( 4{a^{3}}+27{b^{2}}≠ \) 0.

In addition, since the cryptographic operation on elliptic curves are done over finite field through coordinate points on elliptic curve, the equation can be transformed into [2, 4]:

\( { y^{2}}=\lbrace {x^{3}}+ax+b\rbrace mod\lbrace p\rbrace \) .

So we can use point set Ep (a,b) to represent the elliptic curve:

\( \lbrace (x,y)|0≤x≤p, 0≤y≤p, and x,y are both integers\rbrace ⨆0 \)

This process empowers the geometric elliptic curves to be shifted into algebra set located in finite field, which makes it possible to be combined with number theory [1, 2, 9].

3. Law of addition

3.1. Four operations in fields

Following are the four Operations in Fields. Addition and Multiplication: the same as the four operations for Euclidean space. Subtraction: require modulo operations for negative numbers: based on definition. Division: require modulo operations for fractions: based on inverse of fraction.

Example:

Find the value of a, in which \( {(-\frac{1}{2})^{2}}-3-9={4^{-1}}+(-12)=6+(-12)≡ \) a mod 23

Modulo of negative numbers: As (-6) = 23 \( × \) (-1) + 17, getting (-6) \( ≡ \) 17 mod 23 according to definition;

Modulo of fractions: As ( \( 4×6 \) ) mod 23 =1, getting 4-1 = 6, 6 is the inverse of 4 under modulo 23;

Hence it is easy to obtain: \( {(-\frac{1}{2})^{2}}-3-9={4^{-1}}+(-12)=6+(-12)≡ \) 17 mod 23;

Thus, the value of a is 17, easy to be calculated [1, 10].

3.2. Point addition

3.2.1. Definition 1. If P, Q \( ∈ \) Ep (k, m), then

M + O = M

If M = (a, b), (a, b) + (a, -b) = O, that is, (a, -b) is the inverse of M under addition, denoted -M

If M = (a1, b1), N = (a2, b2), M ≠ N, then M + N = (a3, b3)

3.2.2. Formula. As the paper has mentioned in 3.2.1., the two point M = (a1, b1) and N = (a2, b2), M + N = (a3, b3) can be precisely calculated by the regular formula below:

\( {a_{3}}=\lbrace {μ^{2}}-{a_{1}}-{a_{2}}\rbrace mod p \)

\( {b_{3}}=\lbrace μ({a_{1}}-{a_{3}})-{b_{1}}\rbrace mod p \)

In which:

\( μ=\frac{{b_{2}}-{b_{1}}}{{a_{2}}-{a_{1}}} mod p \)

3.3. Point doubling

3.3.1. Algebra formula. Similar with 3.2.2., the two points, which have the same coordinates, M = (a1, b1) and N = (a1, b1), M + N = (a3, b3) is defined by the following calculation:

\( {a_{3}}=\lbrace {μ^{2}}-{2a_{1}}\rbrace mod p \)

\( {b_{3}}=\lbrace μ({a_{1}}-{a_{3}})-{b_{1}}\rbrace mod p \)

In which:

\( μ=\frac{3a_{1}^{2}+k}{2{b_{1}}} mod p \)

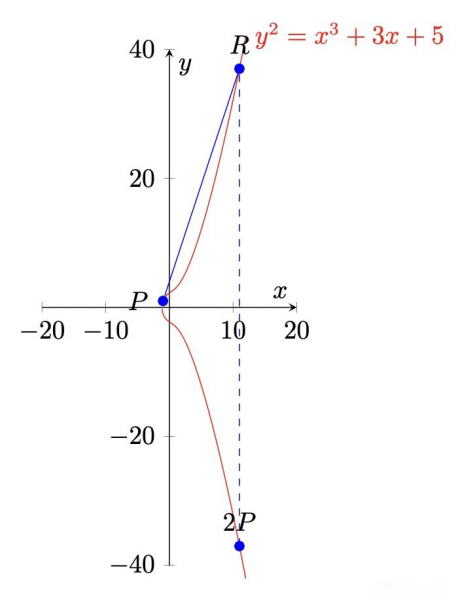
Geometric Example [11]: Question: \( {y^{2}}={x^{3}}+3x+5; P=(-1,1) \) , calculate 2P

The common steps of the calculation is as follows:

Find the tangent over point P by derivation : y’ = 3x2 + 3;

Find another intersection of the tangent and elliptic curves;

Find the point Q, which satisfies: Q and R are symmetric with respect to the x-axis;

Therefore, according to the law of addition, Q = 2P.

These are the corresponding Process:

Derivation: \( f \prime (-1)=3×{(-1)^{2}}+3=6 \)

Get the tangent equation: PR: \( y=6x+12 \)

System of simultaneous equations :

\( \begin{cases} \begin{array}{c} y=6x+12 \\ { y^{2}}={x^{3}}+3x+5 \end{array} \end{cases} \)

Calculate the result: \( x={x_{2p}} , y=-{y_{2p}} \)

3.4. Point multiplication

Point multiplication can be a function based on Point Addition: If M is a point on an elliptic curve, the multiplication over M is calculated by the repeated addition [2]:

\( nM=M+M+M+⋯ +n times \)

4. Elliptic curve discrete logarithm problem

4.1. Discrete logarithm problem (DLP)

4.1.1. Discrete logarithm. If there exists a random integer p being relatively prime to q, while n is a primitive root of q, exactly a number \( μ \) among the sequence 0, 1, 2, ..., \( Φ(n)-1 \) , in which \( Φ(n) \) is named as a totient function, can be recognized to satisfy that \( p≡{n^{μ}}(mod q) \) . Thereby, the number \( μ \) is then defined as the discrete logarithm of p with respect to the base n modulo q, denoted \( μ=in{d_{n}}p(mod q) \) [12].

4.1.2. Mathematical principles of discrete logarithm encryption. Given positive integers x, y, p > 1, to find the positive integer k > 1, satisfying: \( y≡{x^{k}}(mod p) \) .

x is the base; k is the private key; y is the public key:

If we know the value of x , k (private key), it is easy to find y (public key), decrypted.

If we know the value of x , y (public key), it is complex to find k (private key), hard to crack [1].

4.2. Elliptic curve discrete logarithm problem (ECDLP)

4.2.1. Definition 2. & encryption principles. ECDLP, which is regarded as the essential mathematical principle of elliptic curve encryption, can be reflected in the form: P, Q are the points on the elliptic curve; k is an integer, satisfying : Q = kP, in which P is the base point, k is the private key, and Q is the public key.

Given k and P, according to the addition laws, it is easy to find Q.

Given P and Q, it is hard to find k (the p in ECC is too large to exhaustively cite k by hand).

4.2.2. Isomorphism attack (IA). Isomorphism Attack can be divided into Prime-field-anomalous Attack, WTP attack, Gaudry, Hess and Smart Weil Descent Attack, while all of them together synchronously aim to simplify ECDLP [1].

If there exist two elliptic curves which are simultaneously defined over K, such as:

\( {E_{1}}: {y^{2}}+{a_{1}}xy+{a_{3}}y={x^{3}}+{a_{2}}{x^{3}}+{a_{4}}x+{a_{6}} \)

\( {E_{2}}: {y^{2}}+\bar{{a_{1}}}xy+\bar{{a_{3}}}y={x^{3}}+\bar{{a_{2}}}{x^{3}}+\bar{{a_{4}}}x+\bar{{a_{6}}} \)

E1 and E2 are called isomorphic over K [1].

The relation between isomorphism and elliptic curves is an equivalent relation defined over K, If there exist two isomorphic elliptic curves (E1 and E2) exist, subsequently their groups E1(K) and E2(K) of K-rational points must be also isomorphic [1, 3].

Through Isomorphism Attack, ECDLP can be simplified to the corresponding DLP, while these attacks are unique in producing ECDLP solvers which are better than Pollard’s rho algorithm for certain elliptic curves [1, 3, 10].

5. EC ElGamal

5.1. Diffie-hellman-merkle key exchange (DHM)

With the help of the secure DHM protocol, two parties can generate a key via an unsecure channel without knowing anything about one another beforehand. In subsequent communications, this key may be used as a symmetric key to encrypt the communication's content [1].

The process is as exemplified as below [2]:

Alice and Bob decide a prime number p and choose a Q on the curve, making p and Q public:

\( {E_{p}}: {y^{2}}={x^{3}}+Ax+B(mod p) \)

Alice and Bob randomly select an integer NA and NB respectively, and keep them not disclosed.

Alice calculates QA=NA \( \cdot \) Q (NA \( \cdot \) Q refers to N times Q, same way as finding 2P), send it to Bob.

Bob calculates QB=NB \( \cdot \) Q, and sends it to Alice.

Bob calculates NA \( \cdot \) QB; Alice calculates NB \( \cdot \) QA

Therefore, Alice and Bob get the public key:

\( {N_{A}}{Q_{B}}={N_{A}}({N_{B}}Q)=({N_{A}}{N_{B}})Q=({N_{B}}{N_{A}})Q={N_{B}}({N_{A}}Q)={N_{B}}{Q_{A}} \)

5.2. ElGamal

ElGamal encryption algorithm is an asymmetric encryption algorithm based on the Difi-Hermann (DHM) key exchange. In 1985, Taher Elgamal proposed the ElGamal algorithm in his paper “A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms”[2].

The safety of ElGamal depends on discrete logarithm problem (DLP) on G, which is an Abelian group of prime order p and g is a generator of G, while ElGamal is consisted of 3 parts, including key generation, encryption and decryption [1].

5.3. EC ElGamal

Elliptic Curve ElGamal is one form of ECC, in which the ElGamal is transplanted to an elliptic curve [1]. Specifically, the concept of EC ElGamal was initially proposed by Neal Koblitz in his paper “Elliptic Curve Cryptosystems” in 1997 [2].

The safety of EC ElGamal depends on the elliptic curve discrete logarithm (ECDLP) on G, while it can be similarly divided into key generation, encryption and decryption as well [4].

5.3.1. Key generation process. Select a elliptic curve to obtain Ep(a, b), embed the plaintext information m into the point Pm on the curve, and then perform an encryption transformation on the point Pm. Take a generator G of Ep(a, b), Ep(a, b) and G as the public parameters, and User A selects: nA as the private key; PA = nAG as the public key [2].

5.3.2. Encryption process. User B firstly sends a message Pm to User A, selects a random positive integer, and generates the following points as ciphertext [4]:

\( {C_{m}}=\lbrace kG,{P_{m}}+k{P_{A}}\rbrace \)

5.3.3. Decryption process. Subtract the multiplication of the first point with the private key from the second point in the ciphertext point pair, then it is easy to obtain:

\( {P_{m}}+k{P_{A}}-{n_{A}}kG={P_{m}}+k({n_{A}}G)-{n_{A}}kG={P_{m}} \)

As the definition emphasized, here multiplied does not equal to simple multiplication in algebra; instead, it should be restricted by the point multiplication mentioned in 3.4., based on point addition.

6. Conclusion

In this paper, basic principles of Elliptic Curve Cryptography have been concisely covered, combining number theory, group theory and elliptic curve together to introduce a frequently-witnessed cryptosystem in modern information world. According to ECC’s complexity and efficiency which have outperformed those of RSA, elliptic curve cryptosystem will make the network communication much safer and more private. Consequently, the Mathematical principles, including point addition, ECDLP, EC ElGamal, to name but a few, are basically elucidated in the article from the perspectives of concept, definition, application and so on. This paper is likely to be helpful especially for novices majoring in Cryptography due to the applied qualitative research and exemplary analysis. Additionally, through the horizontal comparison with RSA, it can be clearly noted that the advantages of ECC are predominant, which deserve a more comprehensive research in the next paper.

Acknowledgement:

Sincere thanks for Prof. Paolo Cascini from Imperial College London, who assists the article in fundamentally establishing a basic framework according to the relevant cryptography lemmas and algorithms. Special appreciation for Prof. Zhenyu Guo from Xi’an Jiaotong University, who inspires the paper to focus on elliptic curve cryptosystem through a view of number theory and a strategy of exemplary analysis. Earnest thanks for Miss. Zhiyun Deng, who reinforces the knowledge foundation of the essay by patiently answering the questions after lectures. Particular appreciation for Mr. Ziru Xing, who carefully guides and subsequently checks the structure, grammar and citation of the whole essay, ensuring the article to be academic and normative.